・　微分の効用　　　　　　　　　　　　　　　　　　　Ｓ．Ｈ氏

　２つの数　（０．９９）⁹⁹　と　（１．０１）^-101　を考える。

　果たして、どちらの方が大きい数なのだろう？

　普通の電卓が手元にあっても、両者の計算は大変だろうが、関数電卓を用いれば、次の
ような値であることが、直ぐ分かる。

　（０．９９）⁹⁹＝０．３６９７２９６３７６・・・

　（１．０１）^-101＝０．３６６０５０７０５２・・・

したがって、（０．９９）⁹⁹　＞　（１．０１）^-101　である。

　このような解法は、電卓の使い方に慣れている現代の中学・高校生にとって、当然考えら
れるものである。

　しかし、この問題は、微分法を用いれば、関数電卓など持ち出さなくても、手計算による解
決が可能である。

　Ｆ(Ｘ)＝(１−Ｘ)⁹⁹(１＋Ｘ)¹⁰¹　とおくと、その導関数 Ｆ’(Ｘ)は、

　Ｆ’(Ｘ)＝２(１−Ｘ)⁹⁸(１＋Ｘ)¹⁰⁰(１−１００Ｘ)

　０＜Ｘ＜０．０１ において、Ｆ’(Ｘ)＞０ より、Ｆ(Ｘ) は単調に増加する。

よって、　Ｆ(０．０１)＞Ｆ(０)＝１　　から、　(０．９９)⁹⁹(１．０１)¹⁰¹＞１

したがって、（０．９９）⁹⁹＞（１．０１）^-101


　微分法と一見無関係とも思える問題なのに、このように鮮やかに微分法が適用されて問
題が解決されることに、映画「セーラー服と機関銃」の薬師丸ひろ子風に言えば、

　『快感〜！！』

とでもなるのであろうか？！


（追記）　広島工業大学の大川研究室から、次のような別解もあるというご指摘をいただい
　　　　　た。

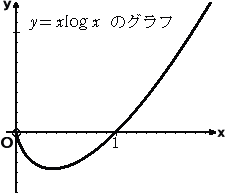
Ｆ(Ｘ)＝Ｘ・ｌｏｇ Ｘ とおく。 　　　真数条件から、Ｘ＞０ である。このとき、 　　　　　Ｆ’(Ｘ)＝ｌｏｇ Ｘ ＋Ｘ・(１/Ｘ) ＝ｌｏｇ Ｘ ＋１ 　　　 　 Ｆ”(Ｘ)＝１/Ｘ ＞０　 　　　　であるので、 　　　Ｆ(Ｘ) は、Ｘ＞０ において常に下に凸である。

このとき、　
　　　　　　

が成り立つ。

　そこで、上式に、Ｘ＝０．９９、Ｙ＝１．０１ を代入すると、

　（０．９９ｌｏｇ０．９９＋１．０１ｌｏｇ１．０１）/２＞０

両辺を２００倍して、９９ｌｏｇ０．９９＋１０１ｌｏｇ１．０１＞０

すなわち、　(０．９９)⁹⁹(１．０１)¹⁰¹＞１ となる。

したがって、　　　（０．９９）⁹⁹　＞　（１．０１）^-101 　が成り立つ。


（注意）　大川研究室によれば、微分を用いない解法もあるとのことであるが、具体的には
　　　　示されなかった。勝手に予想すれば、多分、次のような解法だろうと思う。

(０．９９)⁹⁹(１．０１)¹⁰¹＝(１−０．０１)⁹⁹(１＋０．０１)¹⁰¹＝(１−０．０００１)⁹⁹(１＋０．０１)²
＝(１−０．０００１)⁹⁹×１．０２０１

ここで、２項定理により、

(１−０．０００１)⁹⁹＝１−０．００９９＋₉₉Ｃ₂(０．０００１)²−・・・−₉₉Ｃ₉₉(０．０００１)⁹⁹

２≦ｋ≦９８ において、

₉₉Ｃ_ｋ(０．０００１)^ｋ÷₉₉Ｃ_ｋ＋１(０．０００１)^ｋ＋１＝１００００(ｋ＋１)/(９９−ｋ)≧３００００/９７＞１

であるので、２≦ｋ≦９８ において、₉₉Ｃ_ｋ(０．０００１)^ｋ−₉₉Ｃ_ｋ＋１(０．０００１)^ｋ＋１＞０

よって、　(１−０．０００１)⁹⁹＞１−０．００９９＞０．９９

したがって、(０．９９)⁹⁹(１．０１)¹⁰¹＞０．９９×１．０２＝１．００９８＞１　から、

　（０．９９）⁹⁹＞（１．０１）^-101

が成り立つ。


（コメント）　微分を使った場合と比べて、やはり計算の冗長さは否めない。「微分」というツ
　　　　　　ールがいかに優れているかを如実に物語っている好例だと思う。


（補遺）　このページを書き上げるのと相前後して、大川研究室から次のような別解をいた
　　　　だいた。（証明一部補足）

　ｋ を自然数とする。このとき、１≦ｎ≦ｋ を満たす自然数 ｎ に対して、

　　０ ＜ Ｘ ＜ １/(２ｋ) ならば、　１＋２ｎＸ ＞ (１−Ｘ)^-ｎ

が成り立つ。実際に、

　ｎ＝１ のとき、左辺−右辺＝１＋２Ｘ−１/(１−Ｘ)＝Ｘ(１−２Ｘ)/(１−Ｘ)

　０ ＜ Ｘ ＜ １/(２ｋ) ≦１/２ なので、１−２Ｘ＞０、Ｘ＞０、１−Ｘ＞０ より、左辺−右辺＞０

となる。よって、ｎ＝１ のとき、不等式は成り立つ。

１≦ｍ≦ｋ−１ を満たす自然数 ｍ について、不等式が成立すると仮定する。

すなわち、０ ＜ Ｘ ＜ １/(２ｋ) ならば、　１＋２ｍＸ ＞ (１−Ｘ)^-ｍ

このとき、０ ＜ Ｘ ＜ １/(２ｋ) ならば、１＋２(ｍ＋１)Ｘ ＞ (１−Ｘ)^-(ｍ＋１)　が成り立つことを示す。

左辺−右辺＝１＋２(ｍ＋１)Ｘ−(１−Ｘ)^-(ｍ＋１)＞１＋２(ｍ＋１)Ｘ−(１＋２ｍＸ)/(１−Ｘ)

　＝Ｘ(１−２(ｍ＋１)Ｘ)/(１−Ｘ)

ｍ＋１≦ｋ 、０ ＜ Ｘ ＜ １/(２ｋ) なので、１−２(ｍ＋１)Ｘ≧１−２ｋＸ＞０

さらにまた、Ｘ＞０、１−Ｘ＞０ なので、左辺−右辺＞０ となり、不等式は成り立つ。

　ｎ ＝１ のとき不等式は成立したので、上の性質を順次適用することにより、

　１≦ｎ≦ｋ を満たす自然数 ｎ に対して、

０ ＜ Ｘ ＜ １/(２ｋ) ならば、　１＋２ｎＸ ＞ (１−Ｘ)^-ｎ　が成り立つことが証明された。

　したがって、０ ＜ Ｘ ＜ １/(２ｋ) ならば、　１＋２ｋＸ ＞ (１−Ｘ)^-ｋ が成り立つ。

　この不等式において、ｋ＝９９ とおくと、１＋２・９９・０．０００１＞ (１−０．０００１)^-99

　０ ＜ ０．０００１ ＜ ０．００１＜１/(２・９９) であることに注意して、

　(１．０１)²＝１．０２０１＞１．０１９８＝１＋２・９９・０．０００１

　　　＞ (１−０．０００１)^-99＝ (０．９９・１．０１)^-99

したがって、　（０．９９）⁹⁹＞（１．０１）^-101　が成り立つ。


（コメント）　とても技巧的ですね。特に、最後の　１−０．０００１＝０．９９×１．０１ という
　　　　　計算には、思わず感嘆のため息をついてしまいました。


　平成１９年度学習院大学理学部の入試問題として、次のような問題が出題された。

　ｘ の方程式　ａ・ｃｏｓ²ｘ＋４ｓｉｎｘ−３ａ＋２＝０　が解を持つような実数ａの範囲を求めよ。

　ある程度の素養があれば、解答へのアプローチ、そして、数式処理が可能な問題で、入
試問題としては良問の部類に入るだろうし、どこ彼処の大学で出題されているであろう伝説
（レジェンド）の問題とも言える。

　私なら次のように解くだろう。

（解）　ｓｉｎｘ＝ｔ　とおくと、−１≦ｔ≦１　で、　ａ（１−ｔ²）＋４ｔ−３ａ＋２＝０　より、

　ａ（ｔ²＋２）＝４ｔ＋２　で、　ｔ²＋２≠０　より、　ａ＝（４ｔ＋２）/（ｔ²＋２）

　ｙ＝（４ｔ＋２）/（ｔ²＋２）　とおくと、　ｙ’＝４（ｔ²−２ｔ＋２）/（ｔ²＋２）²＞０

よって、ｙは、単調に増加し、値域は、　−２/３≦ｙ≦２

したがって、題意を満たすためには、　−２/３≦ａ≦２　となる。　　（終）


　多分、上記の解答は、ほとんどの人が行うものと推察される。これに対して、次のような解
答も可能だろう。

（別解）　ｓｉｎｘ＝ｔ　とおくと、−１≦ｔ≦１　で、　ａ（１−ｔ²）＋４ｔ−３ａ＋２＝０

　　すなわち、　ａｔ²−４ｔ＋２ａ−２＝０

　ａ＝０　のとき、　−４ｔ−２＝０　より、　ｔ＝−１/２　で解があるので、ａ＝０　は適。

　ａ≠０　のとき、２次方程式　ａｔ²−４ｔ＋２ａ−２＝０　が、−１≦ｔ≦１　で解を持つ条件を
求めればよい。

　放物線 Ｆ（ｘ）＝ａｔ²−４ｔ＋２ａ−２　の軸の方程式は、　ｔ＝２/ａ

　２/ａ≦−１　すなわち、　２ａ≦−ａ²　より、　−２≦ａ＜０　のとき、

Ｆ（−１）Ｆ（１）≦０　すなわち、　（３ａ＋２）（３ａ−６）≦０　より、　−２/３≦ａ≦２

　よって、　−２/３≦ａ＜０

　２/ａ≧１　すなわち、　２ａ≧ａ²　より、　０＜ａ≦２　のとき、

Ｆ（−１）Ｆ（１）≦０　すなわち、　（３ａ＋２）（３ａ−６）≦０　より、　−２/３≦ａ≦２

　よって、　０＜ａ≦２

　−１＜２/ａ＜１　すなわち、　−ａ²＜２ａ＜ａ²　より、　ａ＜−２、２＜ａ　のとき、

　判別式 Ｄ/４＝４−ａ（２ａ−２）＝−２（ａ²−ａ−２）＝−２（ａ−２）（ａ＋１）＜０

なので、解を持つことはない。

以上から、求める範囲は、　−２/３≦ａ≦２　となる。　　（終）


（コメント）　もちろん、この別解もありなのだが、本解に比べてその煩雑さは計り知れない。
　　　　　微分の効用を実感するときであろう。