自然対数表を作ろう 
底が 10 の常用対数だと、 log102=0.3010 、log103=0.4771 、 ・・・ という
風に、すらすらそらんじていられる方も多いと思うが、底が Napier の数 e の自然対数だ
と、loge2 の値すら、1より小さそうという実感はあるが、その値を常用対数並みにそらん
じていられる方は多分そんなにはいないだろうと思う。
loge2 =0.693146・・・
という値であるが、この値は、実際どんな方法で求めているのであろうか?
その方法が分かれば、自然対数表を自前で作成することも可能となる。
このページでは、次のような数表(小数第3位まで正しい値)
|
| X |
logeX |
|
X |
logeX |
| 1 |
0.000 |
|
11 |
2.397 |
| 2 |
0.693 |
|
12 |
2.484 |
| 3 |
1.098 |
|
13 |
2.564 |
| 4 |
1.386 |
|
14 |
2.639 |
| 5 |
1.609 |
|
15 |
2.708 |
| 6 |
1.791 |
|
16 |
2.772 |
| 7 |
1.945 |
|
17 |
2.833 |
| 8 |
2.079 |
|
18 |
2.890 |
| 9 |
2.197 |
|
19 |
2.944 |
| 10 |
2.302 |
|
20 |
2.995 |
|
の作成を試みるつもりである。
関数電卓を用いれば数表を作ることは簡単であるが、もちろん、それは本意ではない。
関数電卓を用いないで、手計算で求めることを主眼とする。
log x (底 e は省略)の値は、定積分
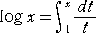
の値として計算される。( → (参考) 直角双曲線の面白い性質 )
上記の定義を用いて、log2 の値を求める場合、通常定積分の近似計算が有効だろう。
台形公式やシンプソンの公式などがよく知られた方法である。
(
→ (参考) モンテカルロ法 )
区間 [1,2] を10等分して、実際に、台形公式から、log2 の近似値を求めると、
log 2 ≒ (0.1)(1/2)(1+2(0.909+0.833+0.769+0.714+0.667
+0.625+0.588+0.556+0.526)+0.5)
より、 log 2 ≒ 0.6937 となる。
台形公式の特徴から、この値は、log2 の真の値よりも若干大きめの値となっている。
計算量が少なく、できるだけ誤差を抑えた形で求める方法が必要とされる。
計算の見通しをよくするために、定積分で定義された対数の式を次のように変形する。
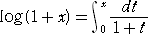
ここで、
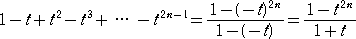
なので、
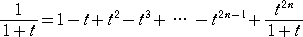
よって、
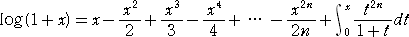
となる。
右辺にある定積分の被積分関数は、十分小さい x に対しては、無視できる値であること
が予想される。
実際に、例えば、n=6 の場合について、グラフを考察すると、
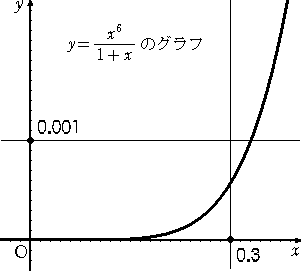
となっている。ただ、どこまで無視できる値かは直ぐには分からないし、もっとも定積分の値
の計算が結構大変そうである。
例えば、x=1 のとき、
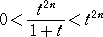 |
なので、 |
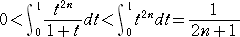 |
よって、

で、log 2 の近似値を計算する場合、その誤差を、0.01以内の範囲で収めようとすれば、
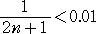
から、n ≧50 となる。
わずか小数点以下第2位まで求める場合でも、n=50 程度の計算が必要になり、手
計算で求めようとするこのページの趣旨からすれば、ちょっと「違うな〜!」という印象を
拭えない。
今度は、x=−1/2 としてみよう。
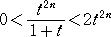 |
なので、 |
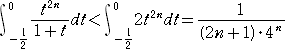 |
よって、n =3 とすると、誤差は、
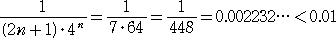
の範囲に収まる。
このとき、
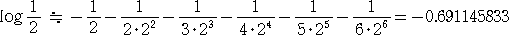
から、 log 2 ≒ 0.69・・・・・・・・ であることが分かる。
n =4 とすれば、誤差は、0.001の範囲に収まり、log 2 ≒ 0.693・・・ である。
(ちょっと、手計算では、分数の計算が大変ですね!)
そこで、もっと計算が少なくて済むような、自然対数の実用的な計算方法が求められる。
上記と同様な計算をして、
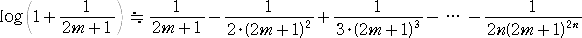
誤差の絶対値は、
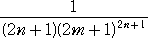
より小さい。
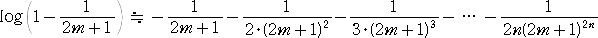
誤差の絶対値は、
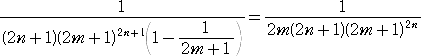
より小さい。
2つの式を辺々引いて、
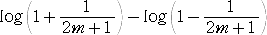
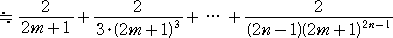
ここで、
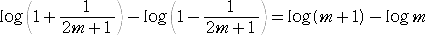
であるので、
この近似式の誤差の絶対値は、
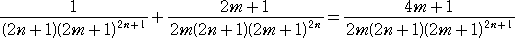
より小さい。 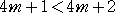 であるので、誤差の絶対値は、
であるので、誤差の絶対値は、
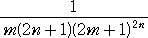
より小さいとしてよい。
この近似式を用いると、順次 log 2 、log 3 、log 4 、・・・ が求められる。
数表は、小数点以下第3位まで正しく求まればよいというスタンスなので、各分数の小数
表示は、小数点以下第5位まで求めればよい。
そうすれば、小数計算による誤差は、0.000005 以内に抑えられる。
m=1 のとき、n=4 とすれば、誤差は、1/(9・38) ≒ 0.0000169 程度である。
このとき、
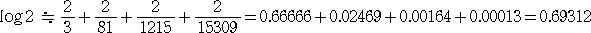
で、誤差は、 0.0000169+0.000005×4=0.0000369 程度に抑えられる。
したがって、 log 2 ≒ 0.693 であるとしてよい。
m=2 のとき、n=3 とすれば、誤差は、1/(2・7・56) ≒ 0.00000457 程度である。
このとき、

で、誤差は、 0.00000457+0.000005×3=0.00001957 程度に抑えられる。
したがって、
log 3 ≒ log 2 +0.40545=1.09845 で、誤差は、0.00005647 以内である。
これより、 log 3 ≒ 1.098 であるとしてよい。
以下同様にして、3個程度の分数計算で、順次に自然数の自然対数が求められる。
計算精度を高めるには、n の値を大きくすればよいが、log 2 の計算のところで、n
=5
位にしておけば十分であると思う。
(参考文献:マルクシェヴィチ 著 宮本敏雄・北原 泰 訳 面積と対数 (東京図書))