直角双曲線の面白い性質 　　　　　　　　　　　　　　　

最近、直角双曲線

について、次のような性質があることを知った。

　　　　　　　　　　　　　　　

　ただし、ａ、ｂ、ｋ　は任意の正の数である。

　定積分の公式を用いれば、直ちに上記性質が成り立つことは了解されるが、ここでは、
面積概念をもとにして上記性質を直感的に把握してみよう。

　いま、ａ＜ｂ　の場合に限定して考える。

　　　


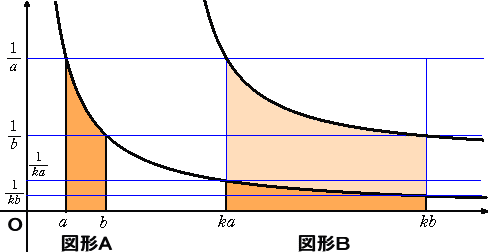
　証明すべき等式の左辺は、図形Ａの面積を表し、右辺は図形Ｂの面積を表す。

　ところで、図形Ｂは図形Ａを横方向に、ｋ倍の拡大・縮小、縦方向に、１/ｋ倍の拡大・縮
小したものなので、面積は不変である。したがって、等式の左辺と右辺は等しい。
（厳密には、区分求積法を用いて証明される。）

　また、ａ＝ｂ　のときは、等式が成り立つことは自明である。　さらに、ａ＞ｂ　のときも、
ａ＜ｂ　の場合と同様に示される。（定積分の上端・下端を交換する公式が用いられる。）

　ところで、自然対数 　を定義する方法はいろいろあるが、次のような定義
は、とても新鮮である。

　　　　　　　　　　　　　　　　

　冒頭で掲げた等式を用いると、対数に関する種々の公式が、ある意味で明快に説明さ
れる。

　面積ということを考えれば、N ＞１　のとき、ｌｏｇ N ＞０　であることは明らかである。

また、　N ＝１　のとき、定積分の性質から、ｌｏｇ N ＝０　が成り立つ。

さらに、N ＜１　のとき、
　　　　　　　　　　　　　　
が成り立つ。

　対数の性質で重要なものは、次にあげられるものであろう。

　Ｍ＞０、Ｎ＞０　で、ｒ は有理数とする。このとき、

　　（１）　　ｌｏｇ ＭN ＝ ｌｏｇ Ｍ ＋ ｌｏｇ N

　　（２）　　ｌｏｇ Ｍ/N ＝ ｌｏｇ Ｍ − ｌｏｇ N

　　（３）　　ｌｏｇ Ｍ^ｒ ＝ ｒ・ｌｏｇ Ｍ

　が成り立つ。

　（上記で、ｒ は有理数としたが、もちろん、ｒ は実数でも成り立つ。しかし、定積分で上記
　　性質を証明するとした場合、やむなく、「ｒ は有理数」という条件に甘んじなければなら
　　ないところが、少し辛いところだ。高校レベルを超える微分積分学（連続関数の性質）
　　を用いれば、ｒ が実数でも成り立つことが示される。）

　実際に、上記性質を、定積分の考え方を用いて証明してみよう。

　（１）の証明：

　

　（２）の証明：

　
　なので、

　　　　　　ｌｏｇ Ｍ/N ＝ ｌｏｇ Ｍ ＋ ｌｏｇ １/N ＝ ｌｏｇ Ｍ − ｌｏｇ N

　（３）の証明： ｒ が自然数のとき、

　

　　　　　

　ｒ ＝０　のときは、明らか。

　ｒ が負の整数のとき、ｒ ＝−ｓ　（ｓ は自然数）とおける。

　このとき、　ｌｏｇ Ｍ^ｒ ＝ ｌｏｇ Ｍ^-s ＝ ｌｏｇ １/Ｍ^s ＝ −ｌｏｇ Ｍ^s ＝ −ｓｌｏｇ Ｍ ＝ ｒ・ｌｏｇ Ｍ

　以上から、 ｒ が整数のとき、（３）は成り立つ。

　 ｒ が有理数のとき、ｒ ＝ｐ/ｑ　（ｐは整数、ｑ は自然数で、ｐ と ｑ は互いに素）とおける。

　このとき、　ｑ・ｌｏｇ Ｍ^ｒ ＝ ｑ・ｌｏｇ Ｍ^ｐ/ｑ ＝ ｌｏｇ Ｍ^q(ｐ/ｑ) ＝ ｌｏｇ Ｍ^ｐ ＝ ｐ・ｌｏｇ Ｍ　より、

　　　　　　　　ｌｏｇ Ｍ^ｒ ＝ （ｐ/ｑ）ｌｏｇ Ｍ ＝ ｒ・ｌｏｇ Ｍ

　以上から、 ｒ が有理数のときも、（３）は成り立つ。

　ところで、１０ を底とする常用対数 ｌｏｇ₁₀ ２、ｌｏｇ₁₀ ３ の値は、近似値で、

　　　　　　　　　ｌｏｇ₁₀ ２＝０．３０１０　、　ｌｏｇ₁₀ ３＝０．４７７１

であることは、よく知られているが、自然対数 ｌｏｇ ２、ｌｏｇ ３ の値が、近似値で、

　　　　　　　　　ｌｏｇ ２＝０．６９３２　、　ｌｏｇ ３＝１．０９８６

であることは、あまり知られていない。（私だけが覚えていないだけかも．．．　(-_-;)　）

　自然対数の底 ｅ は、
　　　　　　　　　　　　　　　　　

となる Ｎ として定義される。

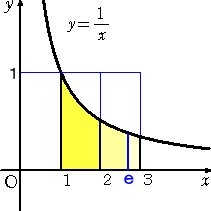　　　左図から明らかなように、長方形の面積と比較して、

　　　　　　　ｌｏｇ ２ ＜ １　であることは明らか。

　　ｌｏｇ ３ については、区間 ［１，３］ を８等分して柱状の
　長方形を作り、値を評価すれば、

　　　　ｌｏｇ ３ ＞ ２８２７１/２７７２０ ＞ １

　　したがって、　２ ＜ ｅ ＜３　であることが分かる。




（参考文献：ア・イ・マルクシェヴィチ　著　宮本敏雄・北原泰彦　訳　面積と対数　（東京図書））