一筆書き　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　図形上のある点を出発して、描いた線と交わってもよいが線は共有しないという条件で、
ある図形が連続な曲線で描かれるとき、その図形は一筆書き可能と言われる。

　次の２つの図形

　　　　　　　　　　　　　

において、左図のものは一筆書き可能であり、右図のものは一筆書き不可能である。

　図形がいつ一筆書き可能かについては、次の定理が知られている。

定理　　線の端点および線と線の交点のうち、奇数本の線が出ている点を 奇点，偶数
　　　　本の線が出ている点を偶点という。このとき、図形が一筆書き可能であるために
　　　　は、次の何れかが成り立てばよい。
　（１）　奇点の個数が、ちょうど ２ である。
　（２）　偶点ばかりである。

　この定理によれば、上図の左側の図形は奇点がちょうど２個あるので一筆書き可能で、
右図の方は奇点が４個なので一筆書き不可能となる。

　一筆書きについて数学的に考えた人としては、オイラーが有名である。「ケーニヒスベル
クの橋」という問題のことを知っている方は多いことと思う。この問題を契機として、数学は
質的な変化を遂げたと言われる。

　それまでの数学は、長さ・面積・角の大きさといった量の概念が問題であったが、一筆書
きの問題は、点同士がどのようにつながっているかという位相の概念が問題の中心になっ
ている。

　一筆書き可能かどうかについては上記の定理があるので、さらなる進展にはあまり興味
がない。

　このページでは一筆書き可能な場合に、その場合の数を求める方法について考察しよう
と思う。

　たとえば、冒頭の図
　　　　　　　　　　　　　　　

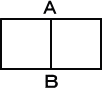
において一筆書きをする場合、一体いくつの場合の数があるだろうか？

　出発点がＡであれば、終着点はＢとなり、出発点がＢであれば、終着点はＡとなる。

出発点がＡのとき、「Ａ→Ｂ」の道の選び方は３通りあり、次に、「Ｂ→Ａ」の道の選び方は２
通り、最後に、「Ａ→Ｂ」の道の選び方は１通りあるので、この場合の一筆書きの方法の数
は、３×２×１＝６（通り）　となる。出発点がＢのときも同様なので、したがって、求める場
合の数は、６＋６＝１２（通り）　となる。

　上記の計算から直ぐ分かるように、ＡとＢを結ぶ線が ｎ 本あれば、一筆書きの方法の数
は、ｎ！×２（通り）ある。

　この問題を少し難しくしたものとして、次のような問題が考えられる。

　　　　　　　　

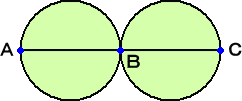
　上記の図形も奇点が２個なので一筆書き可能である。その方法は何通りあるだろうか？

　出発点をＡとする。このとき、「Ａ→Ｃ」の道の選び方の場合は、

　　　　　　Ａ→Ｂ→Ａ→Ｂ→Ｃ→Ｂ→Ｃ　　、　　Ａ→Ｂ→Ｃ→Ｂ→Ａ→Ｂ→Ｃ

の２つの場合しかない。

　よって、　３×２×１×３×２×１＋３×３×２×２×１×１＝３６＋３６＝７２（通り）

　出発点がＣの場合も同様で、求める場合の数は、　７２＋７２＝１４４（通り）となる。

　今度は、次の図形ではどうだろうか？

　　　

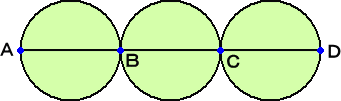
　出発点をＡとする。このとき、「Ａ→Ｄ」の道の選び方の場合は、

　Ａ→Ｂ→Ａ→Ｂ→Ｃ→Ｂ→Ｃ→Ｄ→Ｃ→Ｄ　　、　　Ａ→Ｂ→Ｃ→Ｂ→Ａ→Ｂ→Ｃ→Ｄ→Ｃ→Ｄ

　Ａ→Ｂ→Ａ→Ｂ→Ｃ→Ｄ→Ｃ→Ｂ→Ｃ→Ｄ　　、　　Ａ→Ｂ→Ｃ→Ｄ→Ｃ→Ｂ→Ａ→Ｂ→Ｃ→Ｄ

の４つの場合しかない。

　よって、その場合の数は、

３×２×１×３×２×１×３×２×１＋３×３×２×２×１×１×３×２×１
　　＋３×２×１×３×３×２×２×１×１＋３×３×３×２×２×２×１×１×１
＝２１６＋２１６＋２１６＋２１６＝８６４（通り）となる。

　出発点がＤの場合も同様で、求める場合の数は、　８６４＋８６４＝１７２８（通り）となる。

　今までの計算結果をまとめてみよう。

　この表を眺めていると、円の個数が１増える毎に、一筆書きの方法の数が１２倍に増え
ていることに気がつく。

　よって、円の個数が ｎ 個のとき、一筆書きの方法の数は、

　　　　　　　　　　　　　１２×１２^ｎ−1＝１２^ｎ（通り）

であることが予想される。果たして、この予想は正しいのだろうか？

　この予想が正しいことを数学的帰納法で示そう。

ｎ＝１　のとき、　６＋６＝１２（通り）で成り立つ。

ｎ＝ｋ（ｋ≧１）のとき成り立つと仮定する。

　ｎ＝ｋ＋１　のときの道の選び方の数は、

　　　　１個の円＋ｋ個の円　または　ｋ個の円＋１個の円　の道の選び方の数

に場合分けすることができる。ただし、この場合、

「Ａ→Ｂ→・・・→Ｃ→Ｄ→Ｃ→・・・→Ｂ→Ａ→Ｂ→・・・→Ｃ→Ｄ」のような道の選び方の数と

「Ａ→Ｂ→Ａ→Ｂ→・・・→Ｃ→Ｄ→Ｃ→Ｄ」のような道の選び方の数は等しいことに注意する。

　このとき、　（３！×（１２^ｋ÷２）＋（１２^ｋ÷２）×３！）×２＝１２^ｋ＋1（通り）　となる。

よって、ｎ＝ｋ＋１　のときも成り立つ。

　以上から、全ての自然数 ｎ に対して、求める場合の数は、１２^ｎ（通り）　である。


　当ＨＰがいつもお世話になっているＫ．Ｓ．さんから、メールで、「オイラーの一筆書きの定
理の拡張」についてのレポートを頂いた。（平成２４年４月１０日付け）

　オイラーの一筆書きの定理の拡張

（１）　奇数点が０個のとき、全ての点から一筆書きが可能でサイクルをつくる。

（２）　奇数点が２個のとき、ある奇数点から始めて、他の奇数点で終わる一筆書きが可能。

（３）　奇数点が２ｎ個（ｎ＞１）のとき、一筆書きは不可能。但し、ｎ回で可能。

（４）　奇数点が、奇数個のグラフは存在しない。

　（１）（２）については、よく知られています。（３）について、２ｎ個の奇数点どうしを、２個の

奇数点を残して奇数点どうしを結ぶと（２）になり、したがって、残った奇数点から始めても、

一筆書きが可能になります。よって、間に追加したｎ−１個の線を通ったのですが、通らな

かったことにすれば、ｎ回で全ての点を通ることができます。（４）について、各点における

辺の個数をすべて足し合わせると総和は偶数になります。なぜなら、一つの辺は２度づつ

数えられているからです。一方、奇数点が奇数個あると総和が奇数となり矛盾します。


　オイラーの多面体定理の拡張（辺で連結した単体）（予想）

　平面図形のとき、　Ｖ（点）−Ｅ（辺）＋Ｆ（面）＝１

　凸多面体のとき、Ｖ（点）−Ｅ（辺）＋Ｆ（面）＝２


　一つにまとめて、更に、胞が複数、曲線、面（膜）が欠いている場合（凹型）も含めて考えて
みました。

　　Ｖ（点）−Ｅ（辺）＋Ｆ（膜）―Ｃ（胞）＝ｆ−ｒ＋Ｐ−Ｒ

が成り立つ。ここで、直観的に、

　　Ｃ＝胞（膜に囲まれた部分）の独立した個数

　　ｆ＝連結した膜（点または辺で隣り合う）の独立した個数

　　ｒ＝小さい輪（一つの辺に一つかけ、はずれない）の個数
　　　　膜がない辺のときは、必ず小さい輪を持つ

　　Ｐ＝要の点（膜を持たない頂点）の個数

　　Ｒ＝大きな輪（膜に囲まれた一つの穴に一つかけ、はずれない）の個数

　これらを、ご検証ください。


例１　立方体の、上と下の膜のみを欠いたとき、　Ｖ（８）−Ｅ（１２）＋Ｆ（４）−Ｃ（０）＝０

　一方、右辺は、　ｆ（１）―ｒ（０）＋Ｐ（０）―Ｒ（１）＝０

例２　立方体の、上と下の膜のみを残したとき、　Ｖ（８）−Ｅ（１２）＋Ｆ（２）−Ｃ（０）＝−２

　一方、右辺はｆ（２）―ｒ（４）＋Ｐ（０）―Ｒ（０）＝−２

例３　立方体の、隣り合う３つの膜を残したとき、　Ｖ（８）−Ｅ（１２）＋Ｆ（３）−Ｃ（０）＝−１

　一方、右辺はｆ（１）―ｒ（３）＋Ｐ（１）―Ｒ（０）＝−１

注：立体を平面化しても、標数は不変だが、数え方（f，r，R，P）に変化がある。平面の形を
　　三角形に限定し、Ｆについての帰納法で証明する。


　平面の直線による分割について、

　　　平面の分割数＝１＋（直線の個数）＋（交点の個数）

　但し、交点の個数＝ｎ重点のとき、ｎ−１個とする。

これを、ご検証ください。

（証明）　オイラーの定理から導くことができる。

　全ての交点を十分に含む大きな円を考えることができるので、直線による円の内部の面
の分割数と同じと考えてもよい。（以下の交点数は通所の意味です）

　そこで、交点の間を辺と考えて、平面グラフなので、

　　Ｖ（交点の数）−Ｅ（辺の数）＋Ｆ（分割された面数）＝１

　ここで、円周上の点とその点に分けられた辺は同じ数あるので、相殺されて、

　　Ｖ（円の内部の交点数）−Ｅ（円の内部の辺数）＋Ｆ（分割された面数）＝１　・・・　（１）

が成り立たちます。各直線ごとに、　１＝（その直線上の辺数）−（その直線上の交点数）が
成り立つので、円内にある全ての直線の本数をＬとして、

　Ｌ＝Σ（直線の辺数）−Σ（直線上の交点数）　　（Σは全ての直線による和）

　直線上の辺は、各直線ごと別々に存在しているので、

　Ｅ（円の内部の辺数）＝Σ（直線の辺数）

　直線上の交点は、重複しているので、ｒ 個の直線によってできた交点の数を、Ｐ_ｒ とおく。

　Ｖ＝Ｐ₂＋Ｐ₃＋・・・＋Ｐ_ｒ　、Σ（直線の辺数）＝２Ｐ₂＋３Ｐ₃＋・・・＋ｒＰ_ｒ

　Ｌ＝Ｅ−（２Ｐ₂＋３Ｐ₃＋・・・＋ｒＰ_ｒ）　より、　Ｅ＝Ｌ＋（２Ｐ₂＋３Ｐ₃＋・・・＋ｒＰ_ｒ）

　これらを（１）に代入すると、

　（Ｐ₂＋Ｐ₃＋・・・＋Ｐ_ｒ）−｛Ｌ＋（２Ｐ₂＋３Ｐ₃＋・・・＋ｒＰ_ｒ）｝＋Ｆ（分割された面数）＝１

　よって、　Ｆ＝１＋Ｌ＋Ｐ₂＋２Ｐ₃＋・・・＋（ｒ−１）Ｐ_ｒ　より、

　　　　Ｆ＝１＋Ｌ（直線の辺数）＋Ｐ（ｒ重交点をｒ−１個として数えた数の和）　　（証終）


　球面の直線による分割について

　　球面の分割数＝２＋（交点の個数）

　但し、直線は大円を意味する。交点の個数は、ｎ重点のとき ｎ−１個とする。


（証明）　オイラーの多面体定理より、凸立体なので、Ｖ−Ｅ＋Ｆ＝２　より、Ｆ＝２＋Ｅ−Ｖ

　　ｒ 個の直線によってできた交点の数を、Ｐ_ｒ とおくと、　Ｖ＝Ｐ₂＋Ｐ₃＋・・・＋Ｐ_ｒ　と分ける

　ことができる。辺は、点Ｐ_ｒ に対して、２ｒ本がつながり一つの、辺の両端に点があるので、

　　Ｅ＝（４Ｐ₂＋６Ｐ₃＋・・・＋２ｒＰ_ｒ）÷２＝２Ｐ₂＋３Ｐ₃＋・・・＋ｒＰ_ｒ

　このとき、　Ｅ−Ｖ＝Ｐ₂＋２Ｐ₃＋・・・＋（ｒ−１）Ｐ_ｒ

　つまり、　Ｆ（平面の数）＝２＋（交点の数）　　（証終）


（追記）　当ＨＰがいつもお世話になっているＨＮ「ＧＡＩ」さんが一筆書きの話題を投稿されま
　　　　した。（平成２７年５月９日付け）

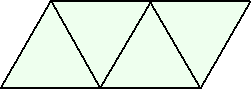　　　左図を見ると、一筆書きがやってみたくなる。
　　　（奇点が２つなのでOK）

　　　さて、一筆書きできる書き順は何通り？



　また、次の場合には何通りになる？

　


　らすかるさんが考察されました。（平成２７年５月９日付け）

　最初の２連の場合は、端の線分の取り方で分類すると、（ちょっとわかりにくいですが）

「−日−」型が4通りでそれぞれ経路は6個　、「＞◇◇」型が4通りでそれぞれ経路は4個
「◇＜＿＞◇」型が1通りで経路は4個

なので、　4×6+4×4+1×4=44通り　となりますね。

　次の５連の場合は考えるのが大変そうなので、とりあえずプログラムで数えました。

1連：6通り
2連：44通り
3連：328通り
4連：2448通り
5連：18272通り
6連：136384通り
7連：1017984通り
8連：7598336通り
9連：56714752通り
10連：423324672通り　　そして、この数列は、「A102591」にありました。

　a[0]=1、 a[1]=6、 a[n+2]=8a[n+1]-4a[n] という漸化式で表せるようです。


　ＧＡＩ さんからのコメントです。（平成２７年５月９日付け）

　うまく読み取れないので理由はわかりませんでしたが、私は馬鹿正直に見落としと、重複
が無いかを点検しながら、44通りのルートを作り出しました。これ以上でも、これ以下でもな
いことを保証できます。

　実際には、出発点と到着点の入れ替えも可能なので、2×44=88（通り）ですよね。

　また、連にしないでも、奇数個の正三角形の図形では、

　　a[0]=1、 a[1]=2、 a[n+2]=2a[n+1]+2a[n]

なる漸化式が構成でき、

a[2]=6
a[3]=16
a[4]=44　（実質、２連図形）
a[5]=120
a[6]=328
a[7]=896
a[8]=2448
a[9]=6688
a[10]=18272 （実質、５連図形）
･････････

より、１０個の５連図形では一筆書き 2×18272=36544（通り）　となり、一日で100通りの行き
方を書いていっても１年では書き切れないパターンが存在する。（→参考：「A002605」）

　この漸化式を考え付く発想力はとても浮かぶ余裕がない。また、この一般項a[n]が

a[n]=((1+√3)^(n+1)-(1-√3)^(n+1))/√3

で表せるなんて思いもよらない。これに興味を抱いたので、今度は正方形の辺どうしをつな
げた図形で一筆書きが可能なものを探すことをやってみました。

ドミノ　  （正方形が2つつながる図形）　1種類中　1（個）
トリオミノ（正方形が3つつながる図形）　2種類中　1（個）
テトロミノ（正方形が4つつながる図形）　5種類中　2（個）
ペントミノ（正方形が5つつながる図形）　12種類中　2（個）
ヘキソミノ（正方形が6つつながる図形）　35種類中　6（個）
ヘプトミノ（正方形が7つつながる図形）　108種類中　4（個）
オクトミノ（正方形が8つつながる図形）　369種類中　17（個）

　どこかに見落としや、勘違いがあるような恐れもありますが、何方か間違いがあれば御指
摘ください。


　らすかるさんからのコメントです。（平成２７年５月１０日付け）

　一筆書き可能について調べました。私のプログラムが正しければ、

ペントミノは、12種類中　3個
ヘプトミノは、108種類中　8個
オクトミノは、369種類中　18個

になると思います。ペントミノはＦ型、Ｗ型、Ｘ型の3個が一筆書きできますね。

Ｆ 型		Ｗ 型		Ｘ 型

　また、オクトミノの先は、

ノノミノ（正方形が9個つながる図形）：1285種類中　28個
デコミノ（正方形が10個つながる図形）：4655種類中　60個
ウンデコミノ（正方形が11個つながる図形）：17073種類中　102個
ドデコミノ（正方形が12個つながる図形）：63600種類中　206個
13-オミノ（正方形が13個つながる図形）：238591種類中　380個
14-オミノ（正方形が14個つながる図形）：901971種類中　752個
15-オミノ（正方形が15個つながる図形）：3426576種類中　1399個

でした。


　ＧＡＩ さんからのコメントです。（平成２７年５月１０日付け）

　へ〜プログラムで調べることができるんですね。凄い！こんな調査にはこの力がないと到底
及ばないですね。

　ペントミノは奇点２個ばかり気を取られていて、偶点のみのXを落としていました。
（またうっかり癖が出ました。）

　ヘプトミノは4個も見落としていたなんて、私の目は節穴に近い。

　オクトミノは17までは見つけていたんですが、18と聞いて再び探すもなかなか見つけられず
やっとの事で最後の１つを発見できました。

　これも18個あるという情報があればこそできることで、ないと見逃す恐れ大です。

　ここまではサイトを利用すれば具体的図形が掲載されていたので出来ますが、それ以上の
なんと15-オミノまでの結果が知れるなんて思ってもいませんでした。一体どれ位の時間を要
したんでしょうか？これを可能にするプログラムを組み上げ、一日以内でこの膨大な計算結
果を出せるなんて驚異です。プログラミンングについての長年の経験とセンスがなければ決
してできる技ではありません。私も真似たいですが、60を過ぎた身には到底無理です。老眼
を武器に地道に数えるしかありません。

　知りたかった思った以上の遥かな世界が見られて嬉しいです。


　らすかるさんからのコメントです。（平成２７年５月１０日付け）

　私にとっては、オクトミノの一筆書きを手作業で調べる方が「凄い！」と思います(笑)
プログラムの実行時間の大半がパターンデータを作る時間で、パターンデータがあれば一筆
書き可能かどうか調べるのはあっという間です。最終版のプログラムでは、パターンデータを
作る時間を含めて、n=10までは一瞬、11までで1秒、12までで4秒、13までで16秒、14までで
1分9秒、15までで5分50秒でした。
（9年前のPCでの実行時間ですので、最新のPCなら1〜2分だと思います。）

　ただし、高速化のためにプログラムを何度も改良していますので、プログラムの作成には
合計で2時間ぐらいかかっています。


　ＧＡＩ さんからのコメントです。（平成２７年５月１０日付け）

　ヘキソミノ３５種類中一筆書きができる図形は次の６タイプに限られる。
では、この６タイプの異なる一筆書きができる描き方の多い順に並べるとどの様になると思
いますか？

（追記）　当ＨＰの掲示板「出会いの泉」に、ＨＮ「QWERTY」さんが「円の内部の分割」と題して
　　　　書き込みをされた。（令和３年７月１８日付け）

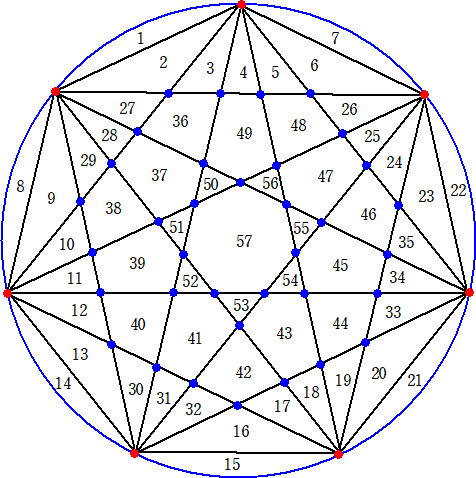
　円周上に７個の点をとり、それらの点をすべて直線で結ぶ。円の内部において、どの３直
線も１点で交わらないとする。このとき、円の内部は、これらの直線によって、何個の部分
に分けられますか。


（コメント）　面白そうだったので、実際に作画して直接数えてみたら、５７個の部分に分かれ
　　　　　　るようだ。

　　　


　直接数えてもよいが、次の公式を用いてもよい。（→　参考）

　平面の直線による分割について、

　　　平面の分割数＝１＋（直線の個数）＋（交点の個数）

　ここで、

　　直線の個数＝₇Ｃ₂＝２１　（←　２つの頂点で直線が１個決まる！）

　　交点の個数＝₇Ｃ₄＝₇Ｃ₃＝３５　（←　４つの頂点で交点が１個決まる！）

　よって、平面の分割数＝１＋２１＋３５＝５７（個）　となる。


　QWERTY さんからのコメントです。（令和３年７月１９日付け）

　この問題は、1999年の灘中学の入試で出題されています。と言ってもこの形のままではな
く、6個の点の場合の図が書いてあって答えが31個であることが書いてあり、その上で7個の
点の場合がきかれています。

　だからかなり易しくはなっていますが、50分で15問のうちの1問で配点は6点です。時間を配
点に比例して割り振れば3分です。3分か5分程度でこの問題を解くのはかなり大変だと思い
ます。灘中学に合格するような子の頭脳は別格であるとは思いますが。

　さて、7個の点をn個の点にした場合の答えを a[n] とします。

　n=1、2、3、4、5、6、7 に対するa[n]は、1、2、4、8、16、31、57 です。

　２項係数 _nＣ_r をC(n,r)で書くことにします。r＞n のときは、C(n,r)=0 とします。

　　a[n]＝C(n-1,0)＋C(n-1,1)＋C(n-1,2)＋C(n-1,3)＋C(n-1,4)

が成り立つそうです。これはどのようにして証明できるのでしょうか。


（コメント）　証明は、（参考）と、上記の計算　１＋₇Ｃ₂＋₇Ｃ₄　で、ご理解ください。

　a[n]＝C(n-1,0)＋C(n-1,1)＋C(n-1,2)＋C(n-1,3)＋C(n-1,4)　は、

　a[n]＝C(n,0)＋C(n,2)＋C(n,4)　　（ただし、C(n,0)=１）

とも式変形できますね！こちらの方が美しいかな．．．？


　Dengan kesaktian Indukmu さんからのコメントです。（令和３年７月１９日付け）

　a[n] = 1 +C(n,2) +C(n,4)　を先に導いてから… という作戦はアリなのでしょうか…。

　公式　C(n,k) = C(n-1,k) +C(n-1,k-1)　を使いますと、

　　1 +C(n,2) +C(n,4) = 1 +C(n-1,2) +C(n-1,1) +C(n-1,4) +C(n-1,3)

ですので。


　Dengan kesaktian Indukmu さんからのコメントです。（令和３年７月２０日付け）

　a[k] が既知だとして、a[k+1] を求めたいものとします。

　点が１個増えるのにともなって弦が何本か、交点が何個か増えるわけですけれども。

　さて、まず a[k] が実現されている図を想定します。

次に、円上に１点を追加し、この点からスタートして、他の点に到達する弦を、１本づつ描い
ていくことを考えます。（順不同で構いません）

　新たに弦を１本描くにあたり、あたかも鉛筆で実際に描くように、スタートする点からニョキ
ニョキと線分を伸ばしていきます。最初は短く、だんだん延長して、最後に既存の点に到達
するようにです。

【１】　この作業の途中に、既存の弦にぶつかる瞬間に以下のことがおこります。
　　・交点が１個発生
　　・分割領域が１個増大。

【２】　この作業の終了時に、すなわち、伸ばしていった線分が既存の点に到達したときに、
　　　以下のことがおこります。すなわち。
　　・弦が１本発生
　　・分割領域が１個増大。

【３】　要するに、弦が１本、または交点が１個増大する都度に、分割領域が１個増大します。

【４】　残りの弦についても同様にして描いていきます。すると、a[k+1]が求まるわけです。

………

　さて、以上より、a[0] = 1　でしたから、

　　《a[n] = 1 +弦の個数 +交点の個数》

と言えます。あとは弦の個数と交点の個数とを、それぞれ求めればおしまいです。

※交点の個数を求めるには、４点を選んでできる四辺形の２本の対角線の交点と１対１対応
　しているところから求められます。

　　……

　難関中学入試というところでは上記のような解き方になるのでしょうか？？


（コメント）　QWERTY さんからの情報によると、

　6個の点の場合の図が書いてあって答えが31個であることが書いてあり、その上で7個の
点の場合がきかれています。

とのことなので、何も難しいことは考えず、力業で、小学生は求めたと考えられます。

　下図は、ｎ＝６の場合に、円周上に１点を追加し頂点同士を結んだものです。

　　　

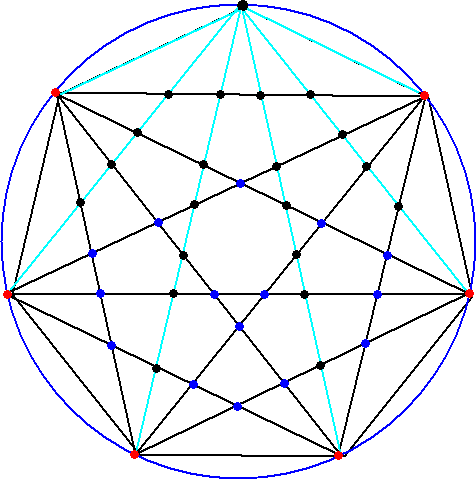
　上図を見ると、線分が全部で２６本増えています。線分が１本増える毎に平面の分割数も
１個増えるので、従って、ｎ＝７の場合の分割数は、　３１＋２６＝５７（個）　となります。

＃これだと十分算数的ですね！


　QWERTY さんからのコメントです。（令和３年７月２０日付け）

　Dengan kesaktian Indukmu さん、ありがとうございます。

　　a[n]=1+弦の個数+交点の個数=1+C(n,2)+C(n,4)

で出来るのですね。意外に簡単なのに驚いています。

　オンライン整数列大辞典で、「1,2,4,8,16,31,57」で検索して見つかったページの先頭に、「パ
スカルの三角形のn行目のはじめの5項の和」とかいてありました。

　後で見たら、1+C(n,2)+C(n,4)　も載ってました。

　これだったら、あるいは、自分でも考えられたかとも思いましたが、多分無理でしょう。
ありがとうございました。

　灘中入試問題も、1+C(7,2)+C(7,4)であっさり解いた小学生もいたのかもしれません。
2000年以降なら塾とかでは、1+C(7,2)+C(7,4)で教えているところもあるでしょう。そうすると、
10秒で解けるごく簡単な問題になってしまいます。


　Dengan kesaktian Indukmu さんからのコメントです。（令和３年７月２０日付け）

　問題文に与えられている6個の点(左回りにB,C,D,E,F,Gと名づけて)の図をぐっとにらみつけ
てから、やおら7個めの点の場所 A を決めます。

　線分ABを描き、領域の個数の増加が 1 であることを確認してメモります。

　線分ACを描き、領域の個数の増加が 5 であることを確認してメモります。

　線分ADを描き、領域の個数の増加が 7 であることを確認してメモります。

　同様にして線分AE、AF、AGについても、領域の個数の増加がいかほどになるかをメモり
ます。

　最後に、メモから領域の個数の増加の総合計を求めます。

　　1+5+7+7+5+1=26

　6点のときの領域数が 31 であることは問題文に与えられているので、求める答えを

　　31+26=57

とします。私が小学校の先生ならば、上のように説明するかもしれません。


　QWERTY さんからのコメントです。（令和３年７月２０日付け）

　Dengan kesaktian Indukmu さん、ありがとうございます。私も同じようにして解きました。

　その後で、31個が与えられてなかったとしてやってみました。

　Aから弦を6本引いて、7

　Bから残りの弦を引いて、5+4+3+2+1

　Cから残りの弦を引いて、7+5+3+1

　Dから残りの弦を引いて、7+4+1

　Eから残りの弦を引いて、5+1

　Fから残りの弦を引いて、1

　これらを全部たして、7+15+16+12+6+1=57

　この作業のときに弦を引いたら1個増える、交点があると1個増えると何となく気づいてた
と思うのですが駄目ですね。


（コメント）　QWERTY さんのような数え方も有りですね！


　ＧＡＩ さんからのコメントです。（令和３年７月２１日付け）

　QWERTY さんの数え方を元にプログラムを組むと、

　　a(n)=n+1+sum(s=1,n-1,sum(i=1,s,(n-s)*i-(n-s-1)))

で走らせれば、

gp > for(n=0,20,print1(a(n)","))

1,2,4,8,16,31,57,99,163,256,386,562,794,1093,1471,1941,2517,3214,4048,5036,6196,・・・

となり、「A000127」で現れる数列が並びますね。


　Dengan kesaktian Indukmu さんからのコメントです。（令和３年７月２１日付け）

　どうも、a[n]=C(n-1,0)+C(n-1,1)+C(n-1,2)+C(n-1,3)+C(n-1,4) をダイレクトに導く方法がある
ようです。

　詳細不明ですけれども、以下のような記述をみかけましたので。

以下の引用は、【４】円の最大分割数（その２）からです。

　図なしに、これ以上説明することは難しいので、結論を述べますが、

　　［参］コンウィイ・ガイ「数の本」シュプリンガー・フェアラーク東京

には、すべての領域にラベルを与えると、ラベルを含む数の個数は、０、１、２、３、４のいず

れかであって、２項係数の和

　　Ｍ_n＝_n-1Ｃ₀＋_n-1Ｃ₁＋_n-1Ｃ₂＋_n-1Ｃ₃＋_n-1Ｃ₄


　上記ページには図がありませんでしたし、また、ラベルのつけかたについても説明があり
ませんでした。

　ちょっと考えてはみたのですが、全くわかりません。

（ひとつの領域に複数のラベルを貼り付ける方法を探しております…）


　QWERTY さんからのコメントです。（令和３年７月２１日付け）

　Dengan kesaktian Indukmu さん、ありがとうございます。いろいろ面白そうなことがありま
すね。

　{a[n]}の階差数列を{b[n]}、{b[n]}の階差数列を{c[n]}とすると、それぞれ

　　「A000125」　、「A000124」

　ケーキをｎ回切って最大何個の部分に分かれるかで、空間図形の立方体と考えたときが
b[n]で、平面図形の正方形と考えたときがc[n]のようです。

　因みに、a[n]は、4次元の立方体の・・・・のようだけどわかりません。

　c[n]は、平面をｎ個の直線で最大何個の部分に分けられるかで、高校数学の漸化式のよ
くある問題で、c[n]=c[n-1]+n　で解くものと思っていました。

　1+n+C(n,2)　でいいということですね。C(n,0)+C(n,1)+C(n,2)　でも、もちろんいいです。b[n]も
こんな感じでできそうかなと思いますが不明です。


　DD++さんからのコメントです。（令和３年７月２３日付け）

　オイラーの定理より導かれる「分割数 = 交点数 + 直線数 + 1」の公式を用いる方法が紹介
されていますが、円の分割の場合は、オイラーの定理を用いずとも、以下でこの公式を理解
することができます。

　円周上の頂点に反時計周りに “0” から “n-1” まで順に番号をつけておきます。分割され
た結果できた各領域に対して、以下のような対応を用意します。

　直線のみで囲まれた領域の場合、まずその領域の辺を反時計回りにぐるぐるなぞります。

　そのとき、進行方向正面にくる頂点の番号はだんだん大きくなりますが、しかし一周に一回
だけ直前より小さくなることがあるはずです。

　その数字が小さくなることが発生する曲がり角が……

　円内部の交点だった場合→領域に、その交点を対応させます。

　円周上の頂点だった場合→領域に、数字が小さくなった直後に通る弦を対応させます。

　弧と一本の弦で囲まれた領域の場合、その弦が……

　“0” と “n-1” を結ぶ弦だった場合→領域に、円そのものを対応させます。

　それ以外だった場合→領域に、その弦を対応させます。

　これにより、分割でできた全領域が、「円内部の交点または弦または円そのもの」と一対一
に対応します。

　したがって、分割数 = 交点数 + 直線数 + 1 が成立します。

＃この理解において、

・交点は 2 つの弦すなわち 4 つの頂点で表現できる

・弦は 2 つの頂点で表現できる

・円そのものは 0 個の頂点で表現できる

となり、このうち “0” がラベル付けされるべき場合はそれをスキップすることにすれば、全領

域が “1” から “n-1” までの n-1 種類のラベル 4 個以下の組の全てを用いてユニークに表

現されるはずです。（“0” をスキップしない方がわかりやすい気もします……）

　件の本のラベル付がこれと一致しているかどうかは知りませんが、多分似たような方法な
んじゃないでしょうか。

　何にせよ、とりあえず私の手元で同等のラベル付けはできましたよ、ということで。


（コメント）　ｎ＝５の場合について、DD++さんのラベル付けを体験してみた。

　分割数は、交点数＋直線数＋１＝５＋１０＋１＝１６　となるが、ラベル付けは下図のよう
になる。
　　　　

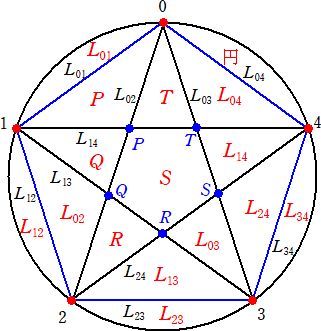
　円の内部の５個の交点Ｐ、Ｑ、Ｒ、Ｓ、Ｔと２頂点間を結ぶ１０個の線分Ｌ₀₁〜Ｌ₃₄を用いて、
領域が巧妙にラベル付けされていることが理解できた。DD++さんに感謝します。


　Dengan kesaktian Indukmu さんからのコメントです。（令和３年７月２５日付け）

　DD++さん、素晴らしいです！！


　Dengan kesaktian Indukmu さんからのコメントです。（令和３年７月２９日付け）

　「A000127」：[1,2,4,8,16,31,57,99,163,256,386,562,794,1093,・・・]　だったのですね！

そして、A055795(n) = A000127(n)-1：[0,1,3,7,15,30,56,98,162,255,385,561,793,1092,・・・]

　「A055795」を使うと、以下のパズルを解くことができます。

　とても強固な新スマホが開発された。販売する前に100階建てのビルの窓から地表まで落
として、落としても壊れない最高の階を調べたい。工場からテスターに４つの新スマホが届い
た。もちろん、壊れない限り、スマホは何度でも落とすことができる。（壊れない限り強度は一
定である。）あらゆる場合において、最高階を決定するまでにスマホを落とす回数の最小値
は、いくつになるか。


　ＧＡＩ さんからのコメントです。（令和３年７月３０日付け）

　「A055795」は使いませんでしたが、8回ですか？また、8回では162階建てのビルまで調査
可能？


　Dengan kesaktian Indukmu さんからのコメントです。（令和３年７月３０日付け）

　はい、おっしゃる通りです。7回では98階建てのビルまで調査可能となります。100階まで調
べるには8回が必要となります。

（参考）　Dissecting Famous Egg Dropping Puzzle - Oursky Code Blog


　DD++ さんからのコメントです。（令和３年７月３１日付け）

　実は、同じ問題が過去に話題に上がったことがあります。（→　参考：「割れない卵」）
是非、ご覧ください。


（追記）　令和３年１１月１３日付け

　一筆書き可能かどうかについては、冒頭の定理から判断出来る。実際の場合について、
一筆書きを実践してみよう。

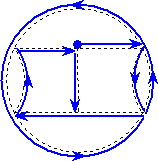
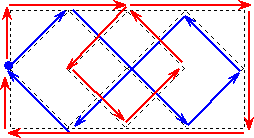
問題　次の図形は一筆書き可能である。一筆書きの手順を一例示せ。

（１）
　　　　

（２）
　　　


（解）（１）
　　　

（２）
　　　



　　　　以下、工事中