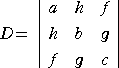曲線・曲面の分類　　　　　　　　　　　　　　　　　　　　　　　　　　

　数学を始め、いろいろなところで様々な曲線や曲面を目にする。その全てをあるルール
に従って分類することは、数学における一つの研究テーマとなりうる。既に、２次曲線や２
次曲面などは、高校から大学初年級の知識があれば分類可能で、その図形が持つ特徴
を理解する一助にもなることだろう。

　このページでは現在知られている、いろいろな図形の分類について、まとめていこうと思
う。

Ａ．２次曲線の分類

　２次曲線については、現在の学習指導要領では、高校３年で学ぶ「数学Ｃ」で完結する。

２次曲線の一般形は、

　　Ｆ（ ｘ ， ｙ ）＝ａｘ²＋２ｈｘｙ＋ｂｙ²＋２ｆｘ＋２ｇｙ＋ｃ＝０

で与えられる。ただし、ａ、ｂ、ｈ は同時に０にならないものとする。

　Ｆ（ ｘ ， ｙ ）＝０　で与えられる曲線の概形には次のようなものがある。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（→参考：「いろいろな曲線」）

　上段の図形は左側から順に、楕円、双曲線、放物線であるが、下段の平行な２直線とい
う場合もあることが意外に見逃しやすい。ましてや最後の重なった２直線という場合も．．．。

　次の問題は、この２直線になる場合を話題にした高校数学の有名問題である。

　ｘ 、ｙ についての２次式 ｘ²−ｘｙ−６ｙ²＋９ｘ＋ｋｙ＋２０ が２つの１次式の積に分解
されるように、定数 ｋ の値を定めよ。

（解）　ｘ についての２次方程式 ｘ²−（ｙ−９）ｘ−６ｙ²＋ｋｙ＋２０＝０　を考える。

　　　判別式を Ｄ とすると、

　　　　　Ｄ＝（ｙ−９）²−４（−６ｙ²＋ｋｙ＋２０）＝２５ｙ²−２（２ｋ＋９）ｙ＋１

　　　題意を満たすためには、ｙ についての２次方程式 Ｄ＝０　が重解を持てばよい。

　　　よって、　（判別式）/４＝（２ｋ＋９）²−２５＝０　より、　ｋ＝−２、−７　（終）


　このような解に私が初めて出会ったのは高校１年のときであった。判別式の判別式．．．
という点に最初戸惑ったが、その美しい解の調べに直ちに虜になってしまった。

　もちろん上記の問題については、次のように解いてもよい。

（別解）　ｙ を含まない部分 ｘ²＋９ｘ＋２０＝（ｘ＋４）（ｘ＋５）　なので、

　　　　ｘ²−ｘｙ−６ｙ²＋９ｘ＋ｋｙ＋２０＝（ｘ＋ａｙ＋４）（ｘ＋ｂｙ＋５）　とおける。

　　　このとき、

　　　　（ｘ＋ａｙ＋４）（ｘ＋ｂｙ＋５）＝ｘ²＋（ａ＋ｂ）ｘｙ＋ａｂｙ²＋９ｘ＋（５ａ＋４ｂ）ｙ＋２０

　　　なので、係数を比較して、　ａ＋ｂ＝−１　、ａｂ＝−６　、　ｋ＝５ａ＋４ｂ

　　　　　ａ＋ｂ＝−１　、ａｂ＝−６　より、　ａ 、ｂ は２次方程式 ｔ²＋ｔ−６＝０　の解で、

　　　（ｔ＋３）（ｔ−２）＝０　より、　ｔ＝−３　、２　となる。

　　　よって、　ａ＝−３　、ｂ＝２　のとき、　ｋ＝５ａ＋４ｂ＝−７

　　　　　　　　　ａ＝２　、ｂ＝−３　のとき、　ｋ＝５ａ＋４ｂ＝−２　　（終）

（コメント）　ｘ²−ｘｙ−６ｙ²＝（ｘ−３ｙ）（ｘ＋２ｙ）　を用いても同様にできる。

　また、当ＨＰがいつもお世話になっているＳ（Ｈ）さんは次のように解くのがお気に入りとい
う。（平成２１年２月２２日付け）

（別解）　　Ｆ（ ｘ ， ｙ ）＝ｘ²−ｘｙ−６ｙ²＋９ｘ＋ｋｙ＋２０＝０　とおく。

　　　　　このとき、　Ｆ（ ｘ ， ｙ ）が２つの１次式の積に分解されるということは、その交点で

　　　　特異点を持つということである。

　　　　　よって、　Ｆ_ｘ（ ｘ ， ｙ ）＝２ｘ−ｙ＋９＝０　、Ｆ_ｙ（ ｘ ， ｙ ）＝−ｘ−１２ｙ＋ｋ＝０

　　　　ｋ＝ｘ＋１２ｙ　を、　Ｆ（ ｘ ， ｙ ）＝０　に代入して、

　　　　　ｘ²−ｘｙ−６ｙ²＋９ｘ＋（ｘ＋１２ｙ）ｙ＋２０＝０　　即ち、　ｘ²＋６ｙ²＋９ｘ＋２０＝０

　　　　さらに、　ｙ＝２ｘ＋９　を代入して整理すると、　２５ｘ²＋２２５ｘ＋５０６＝０

　　　　　（５ｘ＋２２）（５ｘ＋２３）＝０　より、　ｘ＝−２２/５　、−２３/５

　　　　　　ｘ＝−２２/５　のとき、　ｋ＝２５ｘ＋１０８＝−２

　　　　　　　　このとき、　Ｆ（ ｘ ， ｙ ）＝（ｘ＋２ｙ＋４）（ｘ−３ｙ＋５）　である。

　　　　　　ｘ＝−２３/５　のとき、　ｋ＝２５ｘ＋１０８＝−７

　　　　　　　　このとき、　Ｆ（ ｘ ， ｙ ）＝（ｘ−３ｙ＋４）（ｘ＋２ｙ＋５）　である。　（終）

（コメント）　この手の問題は、判別式を使うか、未定係数法を使うかのどちらかだと思って
　　　　　　いましたが、特異点と考えても計算できるという新しい視点を得て、感動しました。
　　　　　　　このような視座をご教示頂いたＳ（Ｈ）さんに感謝します。

　さて、
　　　　　　Ｆ（ ｘ ， ｙ ）＝ａｘ²＋２ｈｘｙ＋ｂｙ²＋２ｆｘ＋２ｇｙ＋ｃ＝０

において、適当に平行移動 ：　（ ｘ ， ｙ ）　→　（ Ｘ ， Ｙ ）

　　　　　　　　Ｘ＝ｘ＋α　、　Ｙ＝ｙ＋β　　（ｘ 軸方向に α 、ｙ 軸方向に β だけ平行移動）

を施すことにより、

　　　　　　Ｇ（ ｘ ， ｙ ）＝ａｘ²＋２ｈｘｙ＋ｂｙ²＋Ｃ＝０

の形に必ず変形することが出来る。ここで、Ｃは定数で、

　　　　　　　　Ｃ＝−ｆ・α−ｇ・β＋ｃ

となることは覚えていて損にはならないだろう。

　また、どれだけ平行移動するかは、次の連立方程式を解けばよい。

　　　　ａｘ＋ｈｙ−ｆ＝０　、　ｈｘ＋ｂｙ−ｇ＝０

例　曲線　５ｘ²−６ｘｙ＋５ｙ²−１４ｘ＋２ｙ＋５＝０　において、

　　　　　　５ｘ−３ｙ＋７＝０　、　−３ｘ＋５ｙ−１＝０

　を解くと、　ｘ＝−２　、ｙ＝−１　なので、　α＝−２　、β＝−１

　　よって、　Ｃ＝７・（−２）−１・（−１）＋５＝−８　より、

　ｘ 軸方向に −２ 、ｙ 軸方向に −１ だけ平行移動すると、もとの曲線は、

　　　　　　５ｘ²−６ｘｙ＋５ｙ²−８＝０

に変換される。（→　参考：「いろいろな曲線」）


　ＨＮ「土筆の子」さんが、上記話題について考察されました。（平成２４年３月２６付け）

　Mathmaticaで計算してみます。±の関係が微妙ではありますが、すっきりしました。

　F (ｘ，ｙ)＝ａｘ²＋２ｈｘｙ＋ｂｙ²＋２ｆｘ＋２ｇｙ＋ｃ＝０　　（ａ，ｈ，ｂ）≠０　において、

これを射影化すると、 ａｘ²＋２ｈｘｙ＋ｂｙ²＋２ｆｘｚ＋２ｇｙｚ＋ｃｚ²＝０

　左辺は、 {x, y, z} {{a, h, f}, {h, b, g}, {f, g, c}} {x, y, z}　と変形できる。

　F (ｘ，ｙ)に対して、平行移動 ：（ｘ ，ｙ）→（Ｘ ，Ｙ）　Ｘ＝ｘ＋α、Ｙ＝ｙ＋β　を施すことにより、

　　　Ｇ（ ｘ ， ｙ ）＝ａｘ²＋２ｈｘｙ＋ｂｙ²＋Ｃ＝０

の形に必ず変形することが出来る。ここで、Ｃは定数で、Ｃ＝−ｆ・α−ｇ・β＋ｃ

このとき、F (ｘ，ｙ)の左辺を、 {{a, h, 0}, {h, b, 0}, {0, 0, C}}　にする操作を行っている

　上の例によれば、　{{5, -3, -7}, {-3, 5, 1}, {-7, 1, 5}}　において、

　　　C = 5 - (-7) (-2) - (1) (-1) = 5 - 14 + 1 = -8

で、 {{5, -3, 0}, {-3, 5, 0}, {0, 0, -8}}　となる。

（コメント）　土筆の子さんに追認していただき、ありがとうございます。


　ＨＮ「土筆の子」さんが、円の標準形について考察されました。（平成２４年３月２９付け）

　先日、代数幾何学の２次超曲面の幾何あたりを勉強しましたので、少し、展開してみます。

　ｘ² + ｙ² + 6ｘ + 4ｙ - 12 = 0　を射影化して、　ｘ² + ｙ² + 6ｘｚ + 4ｙｚ - 12ｚ² = 0
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(* あとで、z=1　と戻す*)

　３×３行列　A₁ = {{1, 0, 3}, {0, 1, 2}, {3, 2, -12}}　として、その行列式　Det[A₁] = -25

　また、２×２行列　A = {{1, 0}, {0, 1}}　として、その行列式　Det[A] = 1

　このとき、　Det[A₁]/Det[A] = -25

　ここで、　Det[A₁]/Det[A] =　c - fα - gβ　が成り立つ。　（→　参考文献）

　　　　　ただし、Ｘ = ｘ + α、Ｙ = ｙ + β とすると、α、βは、連立方程式
　　　　ａｘ＋ｈｙ−ｆ＝０　、　ｈｘ＋ｂｙ−ｇ＝０　の解。

　上記に適用すると、α = 3　、β = 2　で、　ｘ² + ｙ² - 25 = 0　となる。

　（参考文献：　硲　文夫（はざまふみお）著　　代数幾何学　（森北出版））


（コメント）　単に平行移動だけだったら、定数項は、Det[A₁]/Det[A] の計算で得られること
　　　　　　に感動しました。


　次に、ｘｙ の項を消去するには、原点中心に角θの回転移動を施せばよい。

ただし、角θは下記の式を満たす鋭角とするのが普通！

　　　　　　　

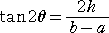
　　特に上式で、 ａ＝ｂ のときは、 θ＝４５°と考える。

例　曲線　５ｘ²−６ｘｙ＋５ｙ²−８＝０　を、原点中心に角４５°回転させると、

　　　　４ｘ²＋ｙ²−４＝０　という楕円の方程式が得られる。

　このように、平行移動と回転移動を施さないと、曲線の概形が判断できないかというと、
実はそうでもない。次のような公式が知られている。

　ａｂ−ｈ²＞０　のとき、　楕円（楕円、円、点の場合を含む）

　ａｂ−ｈ²＜０　のとき、　双曲線（双曲線、交わる２直線の場合を含む）

　ａｂ−ｈ²＝０　のとき、　放物線（放物線、平行な２直線の場合を含む）


例　曲線　５ｘ²−６ｘｙ＋５ｙ²−１４ｘ＋２ｙ＋５＝０　において、

　　ａｂ−ｈ²＝２５−９＝１６＞０　なので、楕円になるだろうことが予想される。


（追記）　平成２４年３月２６日付け

　上記の公式をもう少し精密化した公式が知られている。

一般の２次曲線の分類

　ａｘ²＋２ｈｘｙ＋ｂｙ²＋２ｆｘ＋２ｇｙ＋ｃ＝０　　（ａ，ｈ，ｂ）≠０　において、

　Δ＝ａｂ−ｈ²　、τ＝ａ＋ｂ

　

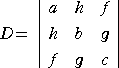
とおく。

（１）　Δ＞０　のとき

　　τＤ＜０　・・・　楕円（円を含む）　、　Ｄ＝０　・・・　１点　、

　　τＤ＞０　・・・　図形無し

（２）　Δ＜０　のとき

　　Ｄ≠０　・・・　双曲線　、　Ｄ＝０　・・・　交わる２直線

（３）　Δ＝０　のとき、合同変換して、　ｂ’ｙ2＋２f’ｘ＋２g’ｙ＋ｃ’＝０

　　Ｄ≠０　・・・　放物線　、　Ｄ＝０　・・・　ｂ’ｃ’−g’2＜０　平行２直線
　　　　　　　　　　　　　　　　　　　　　　　　　ｂ’ｃ’−g’2＝０　１直線
　　　　　　　　　　　　　　　　　　　　　　　　　ｂ’ｃ’−g’2＞０　図形無し


　土筆の子さんが、「２次曲線の分類」について考察されました。（平成２４年４月８日付け）

　ａｘ²＋２ｈｘｙ＋ｂｙ²＋２ｆｘ＋２ｇｙ＋ｃ＝０　を射影化すると、

　　ａ(ｘ/ｚ)² + 2ｈ(ｘ/ｚ)(ｙ/ｚ) + ｂ(ｙ/ｚ)² + 2ｆ(ｘ/ｚ) + 2ｇ(ｙ/ｚ) + ｃ = 0

　上の式に、ｚ²をかけて、（あとで、ｚ=1にもどす。）

　　ａｘ²＋２ｈｘｙ＋ｂｙ²＋２ｆｘｚ＋２ｇｙｚ＋ｃｚ²＝０

　行列  {{a, h, f}, {h, b, g}, {f, g, c}}を考えるが、以下のように一般化しておく。

　　A= {{a₁₁, a₁₂, a₁₃}, {a₂₁, a₂₂, a₂₃}, {a₃₁, a₃₂, a₃₃}}

　また、{x,y,z}を、{x₁,x₂,x₃}としておく。以下のように、X₁、X₂、X₃及びD₁、D₂、D₃をとる。

　　X₁ = x₁ + (a₁₂/a₁₁) x₂ + (a₁₃/a₁₁) x₃
　　X₂ = x₂ + {(a₂₃a₁₁ - a₁₂a₁₃)/(a₂₂a₁₁ - a₁₂a₂₁)} x₃
　　X₃ = x₃

　　D₁ = a₁₁
　　D₂ = a₂₂a₁₁ - a₁₂a₂₁
　　D₃ = Det[A]

　すると、　D₁X₁²+(D₂/D₁)X₂²+(D₃/D₂)X₃²　と表せる。

　具体例を考える。

例１：　5-14ｘ+5ｘ²+2ｙ-6ｘｙ+5ｙ² = 0　を射影化すると、5ｚ²-14ｘｚ+5ｘ²+2ｙｚ-6ｘｙ+5ｙ² =0

　A={{5,-3,-7},{-3,5,1},{-7,1,5}}　で、D₁ = 5　、D₂ = 16　、D₃ = -128

　このとき、　5X₁²+(16/5)X₂²-8X₃²　と表せる。ここで、X₃ に 1 を代入して、

　　　　5X₁²+(16/5)X₂²-8

例２：　ｘ²+ｙ²+6ｘ+4ｙ-12=0　を射影化すると、ｘ²+ｙ²+6ｘｚ+4ｙｚ-12ｚ²=0

　A={{1,0,3},{0,1,2},{3,2,-12}}　で、D₁ = 1　、D₂ = 1　、D₃ = -25

　このとき、　X₁²+X₂²-25X₃²　と表せる。ここで、X₃ に 1 を代入して、X₁²+X₂²-25

　ここのD₁、D₂、D₃は、それぞれ、1×1、2×2、3×3行列の行列式です。

　これと行列の固有値の関係は、考察中です。

参考：硲文夫著、代数幾何学、４章


　さて、回転移動により変換される方程式を求めることは、計算が煩雑で面倒である。もう
少し楽ができないものだろうか？

　まず、次の事実が知られている。

　２次式　ａｘ²＋２ｈｘｙ＋ｂｙ²　に、変換　（ ｘ ， ｙ ）　→　（ Ｘ ， Ｙ ）

　　　　　　　　

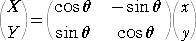
を施して得られる２次式　Ａｘ²＋２Ｈｘｙ＋Ｂｙ²　について、次が成り立つ。

　　（１）　Ａ＋Ｂ＝ａ＋ｂ

　　（２）　ＡＢ−Ｈ²＝ａｂ−ｈ²

（すなわち、回転により、ａ＋ｂ 、ａｂ−ｈ²　は不変な値となる！）

（証明）　ｘ＝Ｘｃｏｓθ＋Ｙｓｉｎθ　、ｙ＝−Ｘｓｉｎθ＋Ｙｃｏｓθ　を、ａｘ²＋２ｈｘｙ＋ｂｙ²　に代入して、

ａ（Ｘｃｏｓθ＋Ｙｓｉｎθ）²＋２ｈ（Ｘｃｏｓθ＋Ｙｓｉｎθ）（−Ｘｓｉｎθ＋Ｙｃｏｓθ）＋ｂ（−Ｘｓｉｎθ＋Ｙｃｏｓθ）²

＝（ａｃｏｓ²θ−２ｈｓｉｎθｃｏｓθ＋ｂｓｉｎ²θ）Ｘ²
　　　　　＋（２ａｓｉｎθｃｏｓθ＋２ｈ（ｃｏｓ²θ−ｓｉｎ²θ）−２ｂｓｉｎθｃｏｓθ）ＸＹ
　　　　　　　　　　＋（ａｓｉｎ²θ＋２ｈｓｉｎθｃｏｓθ＋ｂｃｏｓ²θ）Ｙ²

＝（ａｃｏｓ²θ−ｈｓｉｎ２θ＋ｂｓｉｎ²θ）Ｘ²
　　　　　＋（ａｓｉｎ２θ＋２ｈｃｏｓ２θ−ｂｓｉｎ２θ）ＸＹ
　　　　　　　　　　＋（ａｓｉｎ²θ＋ｈｓｉｎ２θ＋ｂｃｏｓ²θ）Ｙ²

　よって、　　Ａ＝ａｃｏｓ²θ−ｈｓｉｎ２θ＋ｂｓｉｎ²θ

　　　　　　　２Ｈ＝ａｓｉｎ２θ＋２ｈｃｏｓ２θ−ｂｓｉｎ２θ＝（ａ−ｂ）ｓｉｎ２θ＋２ｈｃｏｓ２θ

　　　　　　　　Ｂ＝ａｓｉｎ²θ＋ｈｓｉｎ２θ＋ｂｃｏｓ²θ

となる。このとき、

　（１）　Ａ＋Ｂ＝ａｃｏｓ²θ−ｈｓｉｎ２θ＋ｂｓｉｎ²θ＋ａｓｉｎ²θ＋ｈｓｉｎ２θ＋ｂｃｏｓ²θ＝ａ＋ｂ

　（２）　ここで、　Ａ−Ｂ＝ａｃｏｓ²θ−ｈｓｉｎ２θ＋ｂｓｉｎ²θ−ａｓｉｎ²θ−ｈｓｉｎ２θ−ｂｃｏｓ²θ

　　　　　　　　　　　　　　＝（ａ−ｂ）（ｃｏｓ²θ−ｓｉｎ²θ）−２ｈｓｉｎ２θ

　　　　　　　　　　　　　　＝（ａ−ｂ）ｃｏｓ２θ−２ｈｓｉｎ２θ

　　なので、　４ＡＢ＝（Ａ＋Ｂ）²−（Ａ−Ｂ）²

　　　　　　　　　　　＝（ａ＋ｂ）²−（（ａ−ｂ）ｃｏｓ２θ−２ｈｓｉｎ２θ）²

　　　　　　　　　　　＝（ａ＋ｂ）²−（ａ−ｂ）²ｃｏｓ²２θ＋４ｈ（ａ−ｂ）ｓｉｎ２θｃｏｓ２θ−４ｈ²ｓｉｎ²２θ

よって、

　　４（ＡＢ−Ｈ²）＝（ａ＋ｂ）²−（ａ−ｂ）²ｃｏｓ²２θ＋４ｈ（ａ−ｂ）ｓｉｎ２θｃｏｓ２θ−４ｈ²ｓｉｎ²２θ
　　　　　　　　　　　　　　　　　−（ａ−ｂ）²ｓｉｎ²２θ−４ｈ（ａ−ｂ）ｓｉｎ２θｃｏｓ２θ−４ｈ²ｃｏｓ²２θ

　　　　　　　　　　＝（ａ＋ｂ）²−（ａ−ｂ）²−４ｈ²

　　　　　　　　　　＝４（ａｂ−ｈ²）

　より、　ＡＢ−Ｈ²＝ａｂ−ｈ²　が成り立つ。　（証終）

（コメント）　ＡＢ−Ｈ²　に直に代入してもよいが、計算が少し大変かな？

　上記の事実から、

　回転移動により、　ａｘ²＋２ｈｘｙ＋ｂｙ²　→　Ａｘ²＋Ｂｙ²　と変換されるとき、

　　Ａ、Ｂ　は、　２次方程式　ｔ²−（ａ＋ｂ）ｔ＋ａｂ−ｈ²＝０　の解である

という公式が得られる。これも知っていれば便利な公式となるだろう。

例　曲線　５ｘ²−６ｘｙ＋５ｙ²−８＝０　において、

　　２次方程式　ｔ²−１０ｔ＋１６＝０　の解は、　８　と　２

　　よって、　回転により、　８ｘ²＋２ｙ²−８＝０　または、　２ｘ²＋８ｙ²−８＝０

　すなわち、　４ｘ²＋ｙ²−４＝０　または、　ｘ²＋４ｙ²−４＝０　に変換される。

（コメント）　ほとんど暗算で変換後の方程式が得られるなんて、アンビリーバブルです！私
　　　　　　が高校生のときは、地道に計算していたのですが．．．。多分数学科の先生方は、
　　　　　　この公式をご存じで、上と同じように暗算で検算していたのでしょうね！


　ところで、２次方程式　ｔ²−（ａ＋ｂ）ｔ＋ａｂ−ｈ²＝０　は、２次の正方行列

　　　　　　　

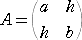
の固有方程式である。（→　参考：「固有ベクトルを求める」）

　実際に、固有方程式　ｄｅｔ（Ａ−ｔＥ）＝０　を計算すると、

　　　　　　ｔ²−（ａ＋ｂ）ｔ＋ａｂ−ｈ²＝０

が得られる。　２次曲線：

　　　Ｆ（ ｘ ， ｙ ）＝ａｘ²＋２ｈｘｙ＋ｂｙ²＋２ｆｘ＋２ｇｙ＋ｃ＝０

は、上記の係数行列 Ａ を用いて、

　　　　　　^ｔｘＡｘ＋^ｔｐｘ＋ｃ＝０

と書ける。ただし、　^ｔｘ＝（ ｘ 　 ｙ ）　、^ｔｐ＝（ ２ｆ 　 ２ｇ ）　とする。

　上記で見たように適当に平行移動することにより、 ^ｔｐｘ の項は消滅させることが出来る。

　よって、与えられた２次曲線を　^ｔｘＡｘ＋Ｃ＝０　と考え、一般性を失うことなく、その形状
を分類してもよいだろう。

　ここで、係数行列 Ａ は、実対称行列であるので、直交行列 Ｐ により対角化される。

すなわち、
　　　　　　　　　

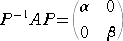
と書ける。ここで、α 、 β は、係数行列 Ａ の固有値である。



　　以下、工事中