拞妛擖帋栤戣偵挧愴両乮偦偺侾乯丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂暯惉俀俆擭俀寧俆擔乮壩乯晅偗挬擔怴暦挬姧偵暯惉俀俆擭搙杻晍拞妛擖帋栤戣偑宖嵹偝傟
偨丅偄偔偮偐柺敀偦偆側栤戣偑偁偭偨偺偱丄彫妛惗偑夝偔儗儀儖偱峫偊偰傒偨丅
侾丏丂枮寧偐傜師偺枮寧傑偱29.53擔偐偐傞傕偺偲偟傑偡丅偁傞塠擭偺俋寧俁侽擔偑枮寧
丂丂偱偁傞偲偒丄師偺枮寧傪侾夞栚偲偟偰丄侾侽侽夞栚偺枮寧偲側傞偺偼丄壗擭屻偺壗寧
丂丂壗擔偱偡偐丅偨偩偟丄塠擭偼係擭偵侾搙昁偢偁傞傕偺偲偟傑偡丅
乮夝乯丂侾侽侽夞栚偺枮寧偲側傞偺偼丄29.53亊100亖2953擔屻
丂丂丂丂嵟弶偺侾擭栚丗365擔丂丄俀擭栚丗365擔丂丄俁擭栚丗365擔丂丄係擭栚乮塠擭乯丗366擔丂丄
丂丂丂丂丂丂丂丂俆擭栚丗365擔丂丄俇擭栚丗365擔丂丄俈擭栚丗365擔丂丄俉擭栚乮塠擭乯丗366擔
丂丂丂丂偐傜丄俉擭屻偺俋寧俁侽擔偑丄2922擔栚丅
丂丂丂丂丂丂2953亅2922亖31丂傛傝丄2953擔屻偼丄俉擭屻偺侾侽寧俁侾擔丂乮廔乯
俀丏丂敿宎偑俁cm偺墌偺廃忋偵揰俙偑偁傝傑偡丅揰俙傪拞怱偲偟偰丄偙偺墌傪30亱夞揮
丂丂偝偣偰偱偒傞墌偑恾偺傛偆偵偁傝傑偡丅墿怓偄晹暘偺柺愊傪媮傔側偝偄丅
丂丂丂丂丂丂
乮夝乯丂懳徧惈偐傜丄塃懁敿暘偺柺愊傪媮傔傟偽廫暘偱偁傞丅
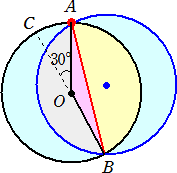 丂丂丂佢俙俷俛亖150亱偐傜丄
丂丂丂佢俙俷俛亖150亱偐傜丄
丂丂丂愵宍俙俷俛偺柺愊亖兾丒32丒乮150/360乯亖15兾/4
丂丂丂仮俙俷俛偺柺愊亖乮1/2乯丒3丒乮3/2乯亖9/4
丂丂丂傛偭偰丄媮傔傞恾宍偺柺愊偼丄
丂丂丂丂2丒乮15兾/4亅9/4乯亖15兾/2亅9/2乮們倣2乯丂乮廔乯
乮嶲峫乯丂彫妛峑偱偼丄墌廃棪兾偼梡偄傜傟偢丄3.14側偺偱丄忋婰偵戙擖偡傟偽丄
丂丂丂丂丂15兾/2亅9/2亖15丒1.57亅4.5亖23.55亅4.5亖19.05乮們倣2乯
乮僐儊儞僩乯丂忋婰偺夝摎偑彫妛惗儗儀儖偐偳偆偐彮偟晄埨丠彫妛惗偵丄30亱丄60亱丄90亱偺
丂丂丂丂丂丂嶰妏宍偺曈偺斾偼婛抦偲偟偰偄偄偺偩傠偆偐丠
俁丏丂俙孨偲俛孨偑倃抧揰傪摨帪偵弌敪偟偰丄倄抧揰傑偱偦傟偧傟堦掕偺懍偝偱曕偒懕
丂丂偗傑偟偨丅俠孨偼俀恖偑弌敪偟偰偐傜俆暘屻偵倃抧揰傪弌敪偟丄堦掕偺懍偝偱憱傝懕
丂丂偗偰俀恖傪捛偄偐偗傑偟偨丅俠孨偼弌敪偟偰俆暘屻偵俛孨偵捛偄偮偒丄偦偺侾侽暘屻
丂丂偵俙孨偵捛偄偮偒傑偟偨丅
乮侾乯丂俙孨丄俛孨丄俠孨偺懍偝偺斾傪偱偒傞偩偗娙扨側惍悢偺斾偱昞偟側偝偄丅
乮夝乯丂俙孨丄俛孨丄俠孨偺懍偝傪偦傟偧傟 倎丄倐丄們 偲偍偔丅
丂丂丂偙偺偲偒丄戣堄傛傝丄丂俆們亖侾侽倐丂丄侾俆們亖俀侽倎丂偡側傢偪丄丂們亖俀倐丂丄俁們亖係倎
丂丂丂丂倎亖乮3/4乯們亖乮3/4乯丒俀倐亖乮3/2乯倐
丂丂丂傛偭偰丄丂倎 丗 倐 丗 們 亖 乮3/2乯倐 丗 倐 丗 2倐 亖 俁 丗 俀 丗 係丂乮廔乯
乮俀乯丂俠孨偼俙孨偵捛偄偮偄偰丄偡偖偵棃偨摴傪摨偠懍偝偱堷偒曉偟傑偟偨丅師偵丄俠孨
丂丂丂偑俛孨偵弌夛偆偺偼丄俠孨偑俙孨偵捛偄偮偄偰偐傜壗暘屻偱偡偐丅暘悢偱摎偊側
丂丂丂偝偄丅
乮夝乯丂俠孨偑俙孨偵捛偄偮偄偰偐傜 倶 暘屻偵俠孨偑俛孨偵弌夛偆偲偡傞偲丄
丂丂丂丂丂丂俀侽倎亅俀侽倐亖倶倐亄倶們丂傛傝丄丂俁侽倐亅俀侽倐亖倶倐亄俀倶倐
丂丂丂丂丂丂丂傛偭偰丄丂倶亖侾侽/俁丂傛傝丄丂侾侽/俁暘屻偵弌夛偆丅丂乮廔乯
乮僐儊儞僩乯丂嶼悢偺栤戣偵曽掱幃傪巊偆偺偼傗偼傝戝恖偘側偄偱偡偹両師偺傛偆偵傕夝偗傞
丂丂丂丂丂丂傛偆偱偡丅
乮暿夝乯丂俙孨丄俛孨丄俠孨偺懍偝傪偦傟偧傟 俁倠丄俀倠丄係倠 偲偍偔丅
丂丂丂丂俠孨偑俙孨偵捛偄偮偄偨偲偒丄俙孨偲俛孨偺娫偺嫍棧偼丄侾侽亊乮係倠亅俀倠乯亖俀侽倠
丂丂丂丂偟偨偑偭偰丄俠孨偑俛孨偵捛偄偮偔偺偼丄丂俀侽倠亐乮係倠亄俀倠乯亖侾侽/俁丂丂乮廔乯
乮僐儊儞僩乯丂偙偪傜偺曽偑旤偟偄夝摎偱偡偹両
乮俁乯丂俠孨偼俛孨偵弌夛偭偰丄偡偖偵傑偨摨偠懍偝偱倄抧揰偵岦偐偭偨偲偙傠丄俙孨偲摨
丂丂丂帪偵倄抧揰偵摓拝偟傑偟偨丅俠孨偺憱偭偨摴偺傝偺崌寁偑俆倠倣偺偲偒丄倃抧揰偐
丂丂丂傜倄抧揰傑偱偺嫍棧傪媮傔側偝偄丅
乮夝乯丂俠孨偑俛孨偵弌夛偭偰偐傜 倷 暘屻偵倄抧揰偵摓拝偟偨偲偡傞丅
丂丂丂俠孨偺憱偭偨摴偺傝偼丄丂侾俆們亄乮侾侽/俁乯們亄倷們亖俆
丂丂丂偝傜偵丄丂俀侽倎亄乮侾侽/俁乯倎亄倷倎亖侾俆們亅乮侾侽/俁乯們亄倷們丂側偺偱丄
丂丂丂丂丂俁侽倐亄俆倐亄乮3/2乯倐倷亖俁侽倐亅乮俀侽/俁乯倐亄俀倐倷
丂丂丂丂傛偭偰丄丂俆亄乮3/2乯倷亖亅俀侽/俁亄俀倷丂傛傝丄丂倷亖俈侽/俁
丂丂丂偙偺偲偒丄丂俁侽倐亄乮俀侽/俁乯倐亄乮侾係侽/俁乯倐亖俆丂傛傝丄丂乮俀俆侽/俁乯倐亖俆
丂丂丂丂丂丂備偊偵丄丂倐亖俁/俆侽
丂丂丂偟偨偑偭偰丄倃抧揰偐傜倄抧揰傑偱偺嫍棧偼丄
丂丂丂俁侽倐亅乮俀侽/俁乯倐亄乮侾係侽/俁乯倐亖俋/俆亅俀/俆亄侾係/俆亖俀侾/俆亖係丏俀乮倠倣乯丂乮廔乯
乮僐儊儞僩乯丂俁丏偺栤戣偼丄俿倁偺僋僀僘斣慻偵巊偊偦偆側栤戣偱偡偹両曽掱幃傪夝偄偰偄傞
丂丂丂丂丂丂偺偱丄彫妛惗儗儀儖偺夝摎偱偼側偄偲抐尵偱偒傑偡偑丄嶼悢揑偵偼偳偆夝偔偺偐
丂丂丂丂丂丂嫽枴偑傢偒傑偡偹両
乮僐儊儞僩乯丂傗偼傝丄忋婰偺夝摎傕廫暘戝恖偘側偄偱偡偹両師偺傛偆偵傕夝偗傞傛偆偱偡丅
乮暿夝乯丂俙孨丄俛孨丄俠孨偺懍偝傪偦傟偧傟 俁倠丄俀倠丄係倠 偲偍偔丅
丂丂丂丂俠孨偑俛孨偵弌夛偭偰偐傜 倷 暘屻偵倄抧揰偵摓拝偟偨偲偡傞偲丄戣堄傛傝丄
丂丂丂丂丂丂丂係倠倷亅俁倠倷亖俁倠亊乮侾侽/俁乯亄係倠亊乮侾侽/俁乯丂側偺偱丄丂倷亖俈侽/俁
丂丂丂丂偙偺偲偒丄俠孨偺憱偭偨摴偺傝偼丄
丂丂丂丂丂丂侾俆亊係倠亄乮侾侽/俁乯亊係倠亄乮俈侽/俁乯亊係倠亖俆丂側偺偱丄丂倠亖俁/侾侽侽
丂丂丂偟偨偑偭偰丄倃抧揰偐傜倄抧揰傑偱偺嫍棧偼丄
丂丂丂丂丂丂俆亅俀亊係亊乮俁/侾侽侽乯亊乮侾侽/俁乯亖俆乕侽丏俉亖係丏俀乮倠倣乯丂乮廔乯
乮僐儊儞僩乯丂傑偩嶼悢儗儀儖偵偼傎偳墦偄偲巚傢傟傞偑懡彮偼嬤偯偄偨偐側丠
乮捛婰乯丂暯惉俀俋擭俆寧係擔晅偗
丂忋婰偺俁丏偺栤戣傪弇惗払偵峫偊偰傕傜偭偨偲偙傠堄奜偲嬯愴偡傞傛偆偩丅巹帺恎傕忋婰
偺夝摎偵枮懌偟偰偄傞傢偗偼側偄偺偱丄嵞搙専摙偟偰傒偨丅
丂挿偄暥復戣偲帪娫偺宱夁偑棈傫偱偔傞偺偱丄栤戣暥傪惍棟偟偰師偺傛偆側恾偵傑偲傔偰傒
偨丅彮偟偼尒捠偟偑傛偔側偭偰峫偊傗偡偔側傞偩傠偆丅
丂丂
乮侾乯丂俙孨丄俛孨丄俠孨偺懍偝偺斾傪偱偒傞偩偗娙扨側惍悢偺斾偱昞偟側偝偄丅
乮夝乯丂忋恾傛傝丄丂倐 丗 們亖侾/侾侽 丗 侾/俆亖侾 丗 俀 側偺偱丄丂們亖俀倐
丂摨條偵偟偰丄丂倎 丗 們亖侾/俀侽 丗 侾/侾俆亖俁 丗 係 側偺偱丄丂倎亖乮俁/係乯們亖乮俁/俀乯倐
丂傛偭偰丄丂倎 丗 倐 丗 們 亖 乮俁/俀乯倐 丗 倐 丗 俀倐 亖 俁 丗 俀 丗 係丂乮廔乯
乮俀乯丂俠孨偼俙孨偵捛偄偮偄偰丄偡偖偵棃偨摴傪摨偠懍偝偱堷偒曉偟傑偟偨丅師偵丄俠孨
丂丂丂偑俛孨偵弌夛偆偺偼丄俠孨偑俙孨偵捛偄偮偄偰偐傜壗暘屻偱偡偐丅暘悢偱摎偊側
丂丂丂偝偄丅
乮夝乯丂倶 暘屻偵俛偲俠偑弌夛偆偲偡傞偲丄忋恾傛傝丄
丂丂丂丂倐倶亄們倶亖俀侽倎亅俀侽倐丂側偺偱丄丂俁倐倶亖侾侽倐丂丂傛偭偰丄倶亖侾侽/俁
乮俁乯丂俠孨偼俛孨偵弌夛偭偰丄偡偖偵傑偨摨偠懍偝偱倄抧揰偵岦偐偭偨偲偙傠丄俙孨偲摨
丂丂丂帪偵倄抧揰偵摓拝偟傑偟偨丅俠孨偺憱偭偨摴偺傝偺崌寁偑俆倠倣偺偲偒丄倃抧揰偐
丂丂丂傜倄抧揰傑偱偺嫍棧傪媮傔側偝偄丅
丂丂倄抧揰傑偱 倷 暘偐偐偭偨偲偒丄忋恾傛傝丄
丂丂丂倷們亖乮侾侽/俁乯們亄乮侾侽/俁乯倎亄倷倎丂側偺偱丄丂俀倷倐亖乮俀侽/俁乯倐亄俆倐亄乮俁/俀乯倷倐
丂丂丂傛偭偰丄丂乮侾/俀乯倷倐亖乮俁俆/俁乯倐丂傛傝丄丂倷亖俈侽/俁
丂丂偙偺偲偒丄俠孨偺憱偭偨摴偺傝偼丄
丂丂丂侾俆們亄乮侾侽/俁乯們亄乮俈侽/俁乯們亖乮侾俀俆/俁乯們亖俆丂傛傝丄丂們亖俁/俀俆
丂傛偭偰丄
丂丂倃倄亖侾俆們亄乮俈侽/俁乯們亅乮侾侽/俁乯們亖乮侾侽俆/俁乯們亖乮侾侽俆/俁乯乮俁/俀俆乯亖俀侾/俆乮倠倣乯
係丏乮侾乯丂僐僀儞偑偨偔偝傫偁傝丄偦偙偐傜俙孨偲俛孨偺俀恖偑岎屳偵僐僀儞傪庢偭偰偄偒
丂丂丂丂傑偡丅侾夞栚偼俙孨偑侾枃丄俀夞栚偼俛孨偑俁枃丄俁夞栚偼俙孨偑俆枃丄係夞栚偼
丂丂丂丂俛孨偑俈枃丄俆夞栚偼俙孨偑俋枃丄丒丒丒偲偄偆傛偆偵丄俀恖偼帺暘偑慜偵庢偭偨枃
丂丂丂丂悢傛傝係枃懡偔僐僀儞傪庢傝傑偡丅壗夞偐庢偭偨屻丄俀恖偺帩偭偰偄傞僐僀儞偺枃
丂丂丂丂悢傪斾傋偨偲偙傠丄嵎偑俁侾枃偱偟偨丅僐僀儞傪懡偔帩偭偰偄傞偺偼偳偪傜偱偡偐丅
丂丂丂丂傑偨丄偦偺恖偑嵟屻偵庢偭偨僐僀儞偼壗枃偱偡偐丅
乮夝乯丂俀値亅侾夞栚偵俙孨偑庢傞僐僀儞偺枃悢偼丄丂侾亄係乮値亅侾乯亖係値亅俁乮枃乯丂側偺偱丄
丂丂丂俀値亅侾夞栚傑偱偵俙孨偑庢傞僐僀儞偺憤悢偼丄丂
丂丂丂丂丂侾亄俆亄丒丒丒丒亄乮係値亅俁乯亖値乮係値亅俀乯/俀亖値乮俀値亅侾乯
丂丂摨條偵偟偰丄
丂丂丂丂俀値夞栚偵俛孨偑庢傞僐僀儞偺枃悢偼丄丂俁亄係乮値亅侾乯亖係値亅侾乮枃乯丂側偺偱丄
丂丂丂俀値夞栚傑偱偵俛孨偑庢傞僐僀儞偺憤悢偼丄丂
丂丂丂丂丂俁亄俈亄丒丒丒丒亄乮係値亅侾乯亖値乮係値亄俀乯/俀亖値乮俀値亄侾乯
丂丂丂値乮俀値亄侾乯亅値乮俀値亅侾乯亖俀値乮嬼悢乯丂偱丄俁侾偵偼側傝摼側偄丅
丂丂丂偦偙偱丄俙孨偑俀値亄侾夞栚偵僐僀儞傪庢偭偨屻偺僐僀儞偺憤悢偼丄乮値亄侾乯乮俀値亄侾乯偱丄
丂丂丂丂丂乮値亄侾乯乮俀値亄侾乯亅値乮俀値亄侾乯亖俀値亄侾亖俁侾
丂丂丂偐傜丄値亖侾俆丂偲側傞丅
丂丂丂丂傛偭偰丄僐僀儞傪懡偔帩偭偰偄傞偺偼丄俙孨偱丄嵟屻偵庢偭偨僐僀儞偺枃悢偼丄
丂丂丂丂丂丂丂係亊乮侾俆亄侾乯亅俁亖俇侾乮枃乯丂乮廔乯
乮僐儊儞僩乯丂彫妛惗偑忋婰偺傛偆偵夝偔偲偼怣偠傜傟側偄偺偱丄懡暘傕偭偲嶼悢揑側夝朄偑
丂丂丂丂丂丂偁傞偺偩傠偆丅
丂師偺傛偆偵峫偊傞偲嶼悢儗儀儖偐側丠偦傫側偵堘傢側偄偐側丠
乮暿夝乯丂俀値亅侾夞栚偵俙孨偑庢傞僐僀儞偺枃悢偼丄丂侾亄係乮値亅侾乯亖係値亅俁乮枃乯丂側偺偱丄
丂丂丂俀値亅侾夞栚傑偱偵俙孨偑庢傞僐僀儞偺憤悢偼丄丂
丂丂丂丂丂侾亄俆亄丒丒丒丒亄乮係値亅俁乯亖値乮係値亅俀乯/俀亖値乮俀値亅侾乯
丂丂丂俀値夞栚傑偱偵俛孨偑庢傞僐僀儞偺憤悢偼丄侾夞摉偨傝俙孨傛傝俀枃偢偮懡偄偐傜丄
丂丂丂丂丂値乮俀値亅侾乯亄俀値亖値乮俀値亄侾乯
丂丂丂嵎偑婏悢偺俁侾屄偵側傞偺偼丄俙孨偑俀値亄侾夞栚偵僐僀儞傪庢偭偨偲偒丅
丂丂丂丂傛偭偰丄丂乮値亄侾乯乮俀値亄侾乯亅値乮俀値亄侾乯亖俀値亄侾亖俁侾丂偐傜丄値亖侾俆丂偲側傞丅
丂丂丂偟偨偑偭偰丄僐僀儞傪懡偔帩偭偰偄傞偺偼丄俙孨偱丄嵟屻偵庢偭偨僐僀儞偺枃悢偼丄
丂丂丂丂丂丂丂係亊乮侾俆亄侾乯亅俁亖俇侾乮枃乯丂乮廔乯
乮俀乯丂僐僀儞偑偨偔偝傫偁傝丄偦偙偐傜俙孨丄俛孨丄俠孨偑弴偵僐僀儞傪庢偭偰偄偒傑偡丅
丂丂侾夞栚偼俙孨偑侾枃丄俀夞栚偼俛孨偑俀枃丄俁夞栚偼俠孨偑係枃丄係夞栚偼俙孨偑
丂丂俉枃丄俆夞栚偼俛孨偑俋枃丄俇夞栚偼俠孨偑侾侾枃丄丒丒丒偲偄偆傛偆偵丄俁恖偼帺暘偑
丂丂慜偵庢偭偨枃悢傛傝俈枃懡偔僐僀儞傪庢傝傑偡丅壗夞偐庢偭偨屻丄俁恖偺帩偭偰偄傞
丂丂僐僀儞偺枃悢傪斾傋偨偲偙傠丄侾斣懡偄恖偲侾斣彮側偄恖偺嵎偑俉俈枃偱偟偨丅
丂丂丂僐僀儞傪堦斣懡偔帩偭偰偄傞偺偼扤偱偡偐丅傑偨丄偦偺恖偑嵟屻偵庢偭偨僐僀儞
丂丂偼壗枃偱偡偐丅峫偊傜傟傞応崌傪偡傋偰摎偊側偝偄丅
乮夝乯丂俁値亅俀夞栚偵俙孨偑庢傞僐僀儞偺枃悢偼丄丂侾亄俈乮値亅侾乯亖俈値亅俇乮枃乯丂側偺偱丄
丂丂丂俁値亅俀夞栚傑偱偵俙孨偑庢傞僐僀儞偺憤悢偼丄丂
丂丂丂丂丂侾亄俉亄丒丒丒丒亄乮俈値亅俇乯亖値乮俈値亅俆乯/俀
丂丂摨條偵偟偰丄
丂丂丂丂俁値亅侾夞栚偵俛孨偑庢傞僐僀儞偺枃悢偼丄丂俀亄俈乮値亅侾乯亖俈値亅俆乮枃乯丂側偺偱丄
丂丂丂俁値亅侾夞栚傑偱偵俛孨偑庢傞僐僀儞偺憤悢偼丄丂
丂丂丂丂丂俀亄俋亄丒丒丒丒亄乮俈値亅俆乯亖値乮俈値亅俁乯/俀
丂丂傑偨丄
丂丂丂丂俁値夞栚偵俠孨偑庢傞僐僀儞偺枃悢偼丄丂係亄俈乮値亅侾乯亖俈値亅俁乮枃乯丂側偺偱丄
丂丂丂俁値夞栚傑偱偵俠孨偑庢傞僐僀儞偺憤悢偼丄丂
丂丂丂丂丂係亄侾侾亄丒丒丒丒亄乮俈値亅俁乯亖値乮俈値亄侾乯/俀
丂丂峫偊傜傟傞応崌偼丄
丂丂丂丒丂俠孨偑嵟戝丄俙孨偑嵟彫偱丄丂値乮俈値亄侾乯/俀亅値乮俈値亅俆乯/俀亖俉俈
丂丂丂丂丂丂俁値亖俉俈丂偱丄値亖俀俋丅
丂丂丂丒丂俙孨偑嵟戝丄俛孨偑嵟彫偱丄丂乮値亄侾乯乮俈乮値亄侾乯亅俆乯/俀亅値乮俈値亅俁乯/俀亖俉俈
丂丂丂丂丂丂俇値亄侾亖俉俈丂偱丄夝側偟丅
丂丂丂丒丂俛孨偑嵟戝丄俠孨偑嵟彫偱丄乮値亄侾乯乮俈乮値亄侾乯亅俁乯/俀亅値乮俈値亄侾乯/俀亖俉俈
丂丂丂丂丂丂俆値亄俀亖俉俈丂偱丄値亖侾俈丅
丂丂埲忋偐傜丄僐僀儞傪堦斣懡偔帩偭偰偄傞偺偼丄俛孨傑偨偼俠孨偱丄
丂丂丂俛孨偑嵟屻偵庢偭偨僐僀儞偼丄丂俈乮値亄侾乯亅俆亖侾俀侾乮枃乯
丂丂丂俠孨偑嵟屻偵庢偭偨僐僀儞偼丄丂俈値亅俁亖俈丒俀俋亅俁亖俀侽侽乮枃乯
乮僐儊儞僩乯丂懡暘丄偙偺栤戣偼彫妛惗偵偲偭偰偼擄栤丠
俆丏丂嶰妏偡偄偺懱愊偼丄乮掙柺愊乯亊乮崅偝乯亐俁偱媮傔傜傟傑偡丅埲壓偺栤偄偵摎偊
丂丂側偝偄丅
丂丂嶰妏偡偄俙-俛俠俢偵偍偄偰丄俙俛亖俇們倣丄俛俠亖俆們倣丄俛俢亖俇們倣偲偟丄曈俙俛丄曈
丂俛俠丄曈俛俢忋偵偦傟偧傟俁揰俹丄俻丄俼傪丄俙俹亖俀們倣丄俛俻亖俁們倣丄俛俼亖俁們倣 偲
丂側傞傛偆偵偲傞丅
乮侾乯丂嶰妏偡偄俙俛俠俢丄嶰妏偡偄俙俛俻俼丄嶰妏偡偄俹俛俻俼偺懱愊偺斾傪偱偒傞偩偗
丂丂丂娙扨側惍悢偺斾偱昞偟側偝偄丅
乮夝乯丂嶰妏偡偄俙俛俠俢偺懱愊傪倁偲偍偔偲丄嶰妏偡偄俙俛俻俼偺懱愊偼丄
丂丂丂丂倁亊乮俁乛俆乯亊乮侾乛俀乯亖乮俁乛侾侽乯倁
丂丂丂丂摨條偵丄嶰妏偡偄俹俛俻俼偺懱愊偼丄
丂丂丂丂乮俁乛侾侽乯倁亊乮俀乛俁乯亖乮侾乛俆乯倁
丂丂丂丂傛偭偰丄俁偮偺嶰妏偡偄偺懱愊偺斾偼丄
丂丂丂丂丂丂丂丂丂丂丂倁丗乮俁乛侾侽乯倁丗乮侾乛俆乯倁亖侾侽 丗 俁 丗 俀丂丂乮廔乯
乮俀乯丂俤俥亖俀俀們倣丄俥俧亖侾俉們倣丄俧俤亖俀侽cm偺仮俤俥俧偺宍傪偟偨巻傪巊偭偰俀偮
丂丂偺嶰妏偡偄傪嶌傝傑偡丅俤俥丄俥俧丄俧俤偺拞揰俵丄俶丄俲傪寢傇慄暘傪愜傝栚偲偟偰
丂丂捀揰俤丄俥丄俧傪堦抳偝偣傞傛偆偵愜偭偰嶌偭偨嶰妏偡偄傪倁1丄俤俥丄俥俧丄俧俤忋偵
丂丂偦傟偧傟俁揰俹丄俻丄俼傪丄俤俹亖侾侽們倣丄俥俻亖俉們倣丄俧俼亖侾俀們倣偲側傞傛偆偵偲
丂丂傝丄嶰妏宍俤俥俧偺宍傪偟偨巻傪慄暘俹俻丄俻俼丄俼俹偱愗傝棧偟丄摨偠挿偝偺曈傪廳
丂丂偹崌傢偣偰嶌偭偨嶰妏偡偄傪倁2偲偟傑偡丅倁1偲倁2偺懱愊偺斾傪偱偒傞偩偗娙扨
丂丂側惍悢偺斾偱昞偟側偝偄丅
乮夝乯丂仮俤俹俼偲仮俤俵俲偺柺愊偺斾偼丄捀妏俤偑嫟捠側偺偱丄丂侾侾亊侾侽丗俉亊侾侽亖侾侾丗俉
丂丂丂傑偨丄柺俤俹俼偵懳偡傞俤俻偺岦偒偲丄柺俤俵俲偵懳偡傞俤俶偺岦偒偼摨偠側偺偱丄
丂丂丂仮俤俹俼丄仮俤俵俲傪掙柺偲偡傞偦傟偧傟偺嶰妏偡偄偺崅偝偺斾偼丄俤俻丗俤俶亖俋丗侾俀
丂丂丂偲側傞丅偟偨偑偭偰丄媮傔傞懱愊偺斾偼丄丂侾侾亊俋丗俉亊侾俀亖俁俁丗俁俀丂偱偁傞丅丂丂乮廔乯
乮僐儊儞僩乯丂嬻娫攃埇偑擄偟偄偱偡偹両仮俤俹俼丄仮俤俵俲傪掙柺偲偟偰丄俀偮偺嶰妏偡偄偺懱
丂丂丂丂丂丂愊傪峫偊傞偙偲偑億僀儞僩偱偟偨丅嶼悢儗儀儖傪辍偐偵挻偊傞挻擄栤偱偡丏丏丏両
俇丏丂俉偮偺柺偑偡傋偰崌摨側惓嶰妏宍偐傜側傞棫懱乮惓俉柺懱乯偵偮偄偰峫偊傑偡丅
丂丂偦傟偧傟偺柺偵偼丄師偺傛偆偵侾偐傜俉傑偱偺悢帤偑彂偐傟偰偄傑偡丅
丂丂丂仮俙俛俠丒丒丒侾丂丄仮俙俠俢丒丒丒俀丂丄仮俙俢俤丒丒丒俁丂丄仮俙俤俛丒丒丒係
丂丂丂仮俥俢俠丒丒丒俆丂丄仮俥俠俛丒丒丒俇丂丄仮俥俛俤丒丒丒俈丂丄仮俥俤俢丒丒丒俉
丂丂偙偺棫懱傪柺俙俛俠偑掙柺偲側傞傛偆偵偍偒傑偡丅掙柺偺偄偢傟偐侾曈傪幉偲偟偰丄
丂椬傝崌偆柺偑掙柺偲側傞傛偆偵偙偺棫懱傪摦偐偡偙偲傪乽揮偑偡乿偲偄偆偙偲偵偟傑偡丅
丂丂丂丂丂丂丂
乮侾乯丂侾夞栚偵曈俙俠傪幉偲偟偰揮偑偟丄懕偗偰俀夞栚偵曈俠俢傪幉偲偟偰揮偑偟傑偟偨丅
丂丂丂偦偺寢壥丄嵟屻偵掙柺偲廳側傞埵抲傪丄壓偺恾偺嶰妏宍偵墿怓偵怓偮偗偟偰帵
丂丂丂偟側偝偄丅傑偨丄偦偺偲偒偺掙柺偵彂偐傟偨悢帤傪摎偊側偝偄丅
乮夝乯丂仮俙俛俠偺壓偺塃懁偺嶰妏宍偱掙柺偵彂偐傟偨悢帤偼丄俆
丂掙柺偑柺俙俛俠偱偁傞忬懺偐傜係夞帺桼偵揮偑偟傑偡丅偙偺偲偒丄埲壓偺乮俀乯丄乮俁乯丄
乮係乯偵摎偊側偝偄丅
乮俀乯丂墿怓晹傾偼丄嵟屻偵掙柺偲廳側傞埵抲偺侾偮偱偡丅傾埲奜偺丄嵟屻偵掙柺偲廳
丂丂丂側傞埵抲慡偰傪丄恾偺嶰妏宍偵墿怓偵怓偮偗偟偰帵偟側偝偄丅傑偨丄傾偺埵抲偵
丂丂丂嵟屻偵廳側傞掙柺偵彂偐傟偨悢帤偲偟偰峫偊傜傟傞傕偺傪偡傋偰摎偊側偝偄丅
乮夝乯
丂丂丂丂丂丂丂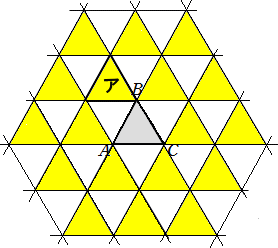
丂丂丂弶婜忬懺偐傜塃夞傝偵揮偑偟偰悢帤偼俈丄嵍夞傝偵揮偑偟偰悢帤偼侾丅
乮俁乯丂係夞帺桼偵揮偑偡揮偑偟曽偼丄慡晹偱壗捠傝偁傝傑偡偐丅偨偩偟丄嵟屻偺掙柺
丂丂丂偺埵抲偑摨偠偱傕丄搑拞偺宱楬偑堘偆応崌偼暿偺揮偑偟曽偲偟傑偡丅
乮夝乯丂俁亊俁亊俁亊俁亖俉侾乮捠傝乯
乮係乯丂嵟屻偵掙柺偲側傞柺偵彂偐傟偨悢帤傪丄乮俁乯偺偡傋偰偺揮偑偟曽偵偮偄偰懌偟
丂丂崌傢偣傑偡丅偦偺榓傪媮傔側偝偄丅
乮夝乯丂掙柺偺悢帤侾偐傜堏傝摼傞悢帤偼丄俀丄係丄俇偺俁捠傝丅
丂丂丂丂掙柺偺悢帤俀偐傜堏傝摼傞悢帤偼丄侾丄俁丄俆偺俁捠傝丅
丂丂丂丂掙柺偺悢帤俁偐傜堏傝摼傞悢帤偼丄俀丄係丄俉偺俁捠傝丅
丂丂丂丂掙柺偺悢帤係偐傜堏傝摼傞悢帤偼丄侾丄俁丄俈偺俁捠傝丅
丂丂丂丂掙柺偺悢帤俆偐傜堏傝摼傞悢帤偼丄俀丄俇丄俉偺俁捠傝丅
丂丂丂丂掙柺偺悢帤俇偐傜堏傝摼傞悢帤偼丄侾丄俆丄俈偺俁捠傝丅
丂丂丂丂掙柺偺悢帤俈偐傜堏傝摼傞悢帤偼丄係丄俇丄俉偺俁捠傝丅
丂丂丂丂掙柺偺悢帤俉偐傜堏傝摼傞悢帤偼丄俁丄俆丄俈偺俁捠傝丅
丂丂偙偺偲偒丄庽宍恾偵傛傝丄掙柺偺悢帤侾偐傜巒傑偭偰係夞帺桼偵揮偑偟偨屻偺掙柺偺悢
丂帤偑丄侾偲側傞傕偺偼俀侾捠傝丄俁偲側傞傕偺偼俀侽捠傝丄俆偲側傞傕偺偼俀侽捠傝丄俈偲側傞傕
丂偺偼俀侽捠傝偱丄偟偨偑偭偰丄嵟屻偵掙柺偲側傞柺偵彂偐傟偨悢帤偺榓偼丄
丂丂丂丂侾亊俀侾亄俁亊俀侽亄俆亊俀侽亄俈亊俀侽亖俁俀侾
乮僐儊儞僩乯丂嶼悢儗儀儖偺偄傠偄傠側夝朄傪峫偊傑偟偨偑丄寢嬊偼庽宍恾棙梡偵棊偪拝偒傑
丂丂丂丂丂丂偟偨丅婡夿揑側寁嶼側偺偱丄帋尡帪娫埲撪偵廫暘夝摎壜擻偲巚傢傟傑偡丅
丂偙偺儁乕僕傪傑偲傔傞偵偁偨傝丄傑偡偄偟偄偝傫偺僽儘僌傪嶲峫偵偝偣偰偄偨偩偄偨丅傑偡
偄偟偄偝傫偵姶幱偟傑偡丅
丂暯惉俀俆擭俇寧俉擔乮搚乯丄揹幵偵忔偭偰搶嫗偵岦偐偭偰偄傞偲偒丄擔擻尋偺峀崘偑栚偵棷
傑偭偨丅敀昐崌妛墍拞妛乮俀侽侾俁擭乯偺擖帋栤戣偱偁傞丅埲壓偼堦晹昞尰傪曄偊偰偄傞丅
丂侾俈摢偺儔僋僟偲堚尵乽挿抝偵侾/俀丄擇抝偵侾/俁丄嶰抝偵侾/俋偢偮梌偊傞丅乿偑堚偝傟偨丅
偦偙偵尗幰偑尰傟丄帺暘偺儔僋僟侾摢傪壛偊偰丄挿抝偵俋摢丄擇抝偵俇摢丄嶰抝偵俀摢偲偒傟
偄偵暘攝偝傟丄尗幰偼偲偰傕姶幱偝傟丄偟偐傕丄帺暘偺儔僋僟傕栠偭偰丄傔偱偨偟傔偱偨偟両
丂偙傟偭偰愄偐傜偁傞桳柤側榖偠傖傫偲巚偭偰撉傫偱偄傞偲丄偙偺榖偵偼懕偒偑偁偭偨傜偟偄丅
丂侾俈摢偺儔僋僟偲堚尵乽挿抝偵侾/俀丄擇抝偵侾/俁丄嶰抝偵侾/俇偢偮梌偊傞丅乿偑堚偝傟偨丅
偦偙偵嬸幰偑尰傟丄尗幰偲摨條偵帺暘偺儔僋僟侾摢傪壛偊偰丄挿抝偵俋摢丄擇抝偵俇摢丄嶰
抝偵俁摢偲暘攝偟偨傕偺偺丄帺暘偺儔僋僟傕幐偭偰偟傑偭偨丅偆乣傫丄巆擮両
丂偦偙偱丄偁側偨偑侾摢偺儔僋僟傪帩偮尗幰偲側傞傛偆偵丄俀俁摢偺儔僋僟傪
丂丂丂乽挿抝偵侾/俀丄擇抝偵侾/倶丄嶰抝偵侾/倷偢偮梌偊傞丅乿
偲偄偆堚尵傪幚峴偡傞偲偒丄倶丄倷 偺抣偼壗偱偟傚偆丠
丂尗幰偲側傞偨傔偵偼丄師偺摍幃
丂丂侾/俀亄侾/倶亄侾/倷亖俀俁/俀係丂乮倶亙倷乯
傪傒偨偡傛偆偵 倶丄倷 偺抣乮惍悢乯傪尒偄偩偣偽傛偄丅
丂偝傜偵丄倶丄倷 偺抣偼摉慠俀係偺栺悢偱丄俁埲忋偱側偗傟偽側傜側偄丅
丂摍幃偐傜丄丂侾/倶亄侾/倷亖侾侾/俀係丂偡側傢偪丄丂乮倶亄倷乯/倶倷亖侾侾/俀係
丂俀係偺栺悢偱丄榓乮倶亄倷乯偑侾侾偱愊乮倶倷乯偑俀係偲側傞偺偼丄丂倶亖俁丄倷亖俉丂偱偁傞丅
乮僐儊儞僩乯丂乽挿抝偵侾/俀丄擇抝偵侾/俁丄嶰抝偵侾/俇偢偮梌偊傞丅乿偲偄偆堚尵偱偼丄嬸幰偵側
丂丂丂丂丂丂偭偰偟傑偄傑偡偹両丏丏丏倖(^^;)丅
丂暯惉俀俇擭俀寧係擔乮壩乯晅偗挬擔怴暦挬姧偵暯惉俀俇擭搙奐惉拞妛擖帋栤戣偑宖嵹偝傟
偨丅崅峑惗懳徾偱傕廫暘捠梡偟偦偆側栤戣偵偮偄偰峫嶡偟偰傒偨丅乮堦晹夵戣乯
侾丏丂俁偮偺惍悢俙丄俛丄俠偑偁傞丅俙偲俛偺嵟戝岞栺悢偼俀侾丄俛偲俠偺嵟戝岞栺悢偼
丂丂俁俆丄俙偲俠偺嵟戝岞栺悢偼俋俉偱偁傞丅偨偩偟丄俙亄俛亄俠亝侾侽侽侽丂偲偡傞丅
丂丂丂偙偺傛偆側惈幙傪帩偮丄俁偮偺惍悢俙丄俛丄俠偺慻傪侾慻媮傔傛丅
乮夝乯丂戣堄傛傝丄丂俙亖俀侾倎亖俁丒俈丒倎丂丄俛亖俀侾倐亖俁丒俈倐丂乮倎丄倐偼屳偄偵慺乯
丂丂丂丂丂丂丂丂丂丂丂俛亖俁俆倐乫亖俆丒俈倐乫丂丄俠亖俁俆們亖俆丒俈們丂乮倐乫丄們偼屳偄偵慺乯
丂丂丂丂丂丂丂丂丂丂丂俙亖俋俉倎乫亖侾係丒俈倎乫丂丄俠亖俋俉們乫亖侾係丒俈們乫丂乮倎乫丄們乫偼屳偄偵慺乯
丂丂忋幃傛傝丄丂俁倎亖侾係倎乫丂丄俁倐亖俆倐乫丂丄俆們亖侾係們乫丂側偺偱丄
丂倎亖侾係丂丄倎乫亖俁丂丄倐亖俆丂丄倐乫亖俁丂丄們亖侾係丂丄們乫亖俆丂偺偲偒丄忦審傪枮偨偡丅
丂偙偺偲偒丄丂俙亖俀俋係丂丄俛亖侾侽俆丂丄俠亖係俋侽丂偱丄俙亄俛亄俠亝侾侽侽侽丂傪枮偨偡丅丂丂乮廔乯
俀丏丂壓恾偼丄俀偮偺愵宍偲嶰妏宍傪慻傒崌傢偣偨傕偺偱偁傞丅屖俹俻亖俆丒屖俻俼偺偲
丂丂偒丄妏兤丄冇偍傛傃俀偮偺愵宍偺柺愊偺榓傪媮傔傛丅偨偩偟丄墌廃棪兾亖俁丏侾係偲
丂丂偡傞丅
丂丂丂丂丂丂
乮夝乯丂忦審傛傝丄丂俀亊俋兾亊冇/俁俇侽亱亖俆亊俀亊俁兾亊兤/俁俇侽亱側偺偱丄丂俁冇亖俆兤
丂丂丂仮俙俛俠偵偍偄偰丄丂俀侽亱亄侾俉侽亱亅冇亖兤丂傛傝丄丂俇侽侽亱亅俁冇亖俁兤
丂丂丂傛偭偰丄丂俉兤亖俇侽侽亱丂傛傝丄丂兤亖俈俆亱丂傑偨丄丂冇亖侾俀俆亱偱偁傞丅
丂丂丂俀偮偺愵宍偺柺愊偺榓偼丄
丂俉侾兾亊冇/俁俇侽亱亄俋兾亊兤/俁俇侽亱亖俉侾兾亊侾俀俆亱/俁俇侽亱亄俋兾亊俈俆亱/俁俇侽亱
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖俀俀俆兾/俉亄侾俆兾/俉亖俁侽兾亖俋係丏俀丂丂乮廔乯
乮僐儊儞僩乯丂屖搙朄傪抦偭偰偄傟偽丄傕偭偲僗僢僉儕偟偨夝摎偵側傞偩傠偆丅
乮捛婰乯丂俽乮俫乯偝傫偐傜丄憗堫揷拞妛乮俀侽侽俉擭搙乯偺擖帋栤戣傪偛徯夘偄偨偩偄偨丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮暯惉俀俈擭侾寧侾俈擔晅偗乯
丂俀偮偺愵宍傪慻傒崌傢偣偨恾偑偁傞丅俙偺愵宍偼敿宎偑侾們倣偱丄柺愊偑俀們噓偱偁傞丅俛
偺愵宍偼敿宎偑侾侽們倣偱偁傞a偺愵宍偺柺愊傪媮傔傛丅扐偟丄墌廃棪偼丄俁丏侾係偲偡傞丅
丂丂丂丂丂丂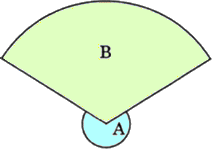
乮夝乯丂愵宍俛傪娷傓摨怱墌偺柺愊偼丄丂侾侽侽亊俁丏侾係亖俁侾係乮們噓乯丂偱偁傞丅愵宍偺柺愊
丂偼乮敿宎乯2偵斾椺偡傞偺偱丄愵宍俙偺敿宎傪侾侽攞偵奼戝偟偨愵宍偺柺愊偼丄
丂侾侽2亊俀亖俀侽侽乮們噓乯偱偁傞丅
丂傛偭偰丄媮傔傞柺愊偼丄俁侾係亅俀侽侽亖侾侾係乮們噓乯丂偱偁傞丅丂丂乮廔乯
乮捛婰乯丂暯惉俀俈擭俀寧俆擔乮栘乯晅偗挬擔怴暦挬姧偵暯惉俀俈擭搙嶗堻拞妛擖帋栤戣偑宖
丂丂丂丂嵹偝傟偨丅媏愳楀偝傫傗嶰塝撧曐巕偝傫側偳偑嶗堻偺懖嬈惗偱偁傞丅乮堦晹夵戣乯
侾丏乮侾乯師偺乮丂丂乯偵偁偰偼傑傞悢傪摎偊側偝偄丅
乮鶣乯丂乷乮俆丏俇亅俀丏俉亊乮侾亄俆/俈乯乯亐乮侾俉/俁俆乯亄乮俀亄俀/俁乯乸亐係丏俈俆亖乮丂丂乯
乮鶤乯丂乮係俈/俆俆亅俉/俀俆亐乮丂丂乯乯亊乮侾俋/俁俇亊俋亅乮侾亄侾/俀係乯亐乮俆/俈乯亄俀/俁乯
丂丂丂亖俀亄俁/俉
乮夝乯乮鶣乯丂嵍曈亖乷乮俀俉/俆亅乮侾係/俆乯亊乮侾俀/俈乯乯亊乮俁俆/侾俉乯亄俉/俁乸亊係/侾俋
丂丂丂丂丂丂丂丂丂亖乮俋俉/俋亅俀俉/俁亄俉/俁乯亊係/侾俋
丂丂丂丂丂丂丂丂丂亖乮俁俉/俋乯亊係/侾俋
丂丂丂丂丂丂丂丂丂亖俉/俋
乮鶤乯丂乮係俈/俆俆亅俉/俀俆亐乮丂丂乯乯亊乮侾俋/係亅乮俀俆/俀係乯亊乮俈/俆乯亄俀/俁乯亖侾俋/俉丂傛傝丄
丂丂乮係俈/俆俆亅俉/俀俆亐乮丂丂乯乯亊乮俋俆/俀係乯亖侾俋/俉丂側偺偱丄
丂丂係俈/俆俆亅俉/俀俆亐乮丂丂乯亖俁/俆
丂傛偭偰丄丂俉/俀俆亐乮丂丂乯亖係俈/俆俆亅俁/俆亖侾係/俆俆丂傛傝丄
丂丂丂乮丂丂乯亖俉/俀俆亊乮俆俆/侾係乯亖係係/俁俆丂丂乮廔乯
乮俀乯丂壓偺恾偺傛偆側傾偐傜働偺俋屄偺儅僗偑偁傝傑偡丅偙偺傾偐傜働偺儅僗偺拞偵丄
丂丂栺悢偑慡晹偱俋屄偁傞惍悢偺栺悢傪彫偝偄弴偵擖傟傑偡丅偙偺偲偒丄師偺乮丂丂乯偵
丂丂偁偰偼傑傞悢傪摎偊側偝偄丅
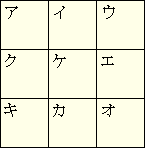 丂丂乮鶣乯丂傾亄働亄僆亖俀係侾 偲側傞惍悢偼乮丂丂乯偱偡丅
丂丂乮鶣乯丂傾亄働亄僆亖俀係侾 偲側傞惍悢偼乮丂丂乯偱偡丅
丂丂乮鶤乯丂僂亊働亊僉亖俁俉係侾俇 偲側傞惍悢偼乮丂丂乯偱偡丅
乮夝乯丂媮傔傞惍悢傪俶偲偡傞偲丄栺悢偑慡晹偱俋屄偁傞偙偲偐傜丄慺悢倫丄倯傪梡偄偰丄
丂丂丂俶亖倫8丂丂傑偨偼丄丂俶亖倫2倯2丂乮倫亙倯乯
乮鶣乯丂俶亖倫8丂偺偲偒丄丂侾丄倫丄倫2丄倫3丄倫4丄倫5丄倫6丄倫7丄倫8
丂俶亖倫2倯2丂乮倫亙倯乯丂偺偲偒丄侾丄倫丄乮倯丂傑偨偼丂倫2乯丄倫倯丄乮倯2丂傑偨偼丂倫2倯乯丄倫倯2丄倫2倯2
丂傛偭偰丄丂侾亄倫4亄倫8亖俀係侾丂偺偲偒丄乮倫4亅侾俆乯乮倫4亄侾俆乯亖侽丂偱丄偙偺幃傪枮偨偡慺
丂丂丂丂丂悢倫偼懚嵼偟側偄丅
丂丂丂丂丂侾亄倫倯亄倫2倯2亖俀係侾丂偺偲偒丄乮倫倯亅侾俆乯乮倫倯亄侾俇乯亖侽丂偱丄丂倫亖俁丄倯亖俆
丂偟偨偑偭偰丄丂俶亖俁2丒俆2亖俀俀俆
乮鶤乯丂俁俉係侾俇亖俀4丒俈4丂偱偁傞偺偱丄俶亖倫8丂偺応崌偼婲偙傝偊側偄丅
丂倯亙倫2丂偺偲偒丄倯2亙倫2倯丂側偺偱丄倯丒倫2倯丒倫2倯2亖倫4倯4亖俀4丒俈4丂傛傝丄倫亖俀丄倯亖俈
丂倯亜倫2丂偺偲偒丄倯2亜倫2倯丂側偺偱丄倫2丒倯2丒倫2倯2亖倫4倯4亖俀4丒俈4丂傛傝丄倫亖俀丄倯亖俈
丂偟偨偑偭偰丄丂俶亖俀2丒俈2亖侾俋俇丂丂乮廔乯
乮僐儊儞僩乯丂夝摎偺巇曽偑偲偰傕彫妛惗揑偱側偄傕偺偵側偭偰偟傑偭偨丅彫妛惗偩偭偨傜丄偳
丂丂丂丂丂丂偆寁嶼偡傞偺偩傠偆丠
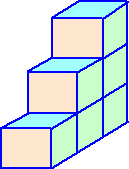
俀丏偄傠偄傠側戝偒偝偺惓嶰妏宍傪丄師偺傛偆偵抲偄偰偄偒傑偡丅偼偠傔偵丄侾曈偺挿偝
丂偑侾們倣偺惓嶰妏宍俁枃乮侾丄俀丄俁乯偲侾曈偺挿偝偑俀們倣偺惓嶰妏宍俀枃乮係丄俆乯傪抲
丂偒傑偡丅師偐傜偼丄偱偒偨恾宍偺嵟傕挿偄曈傪侾曈偲偡傞惓嶰妏宍傪傕偲偺恾宍偺偲
丂側傝偵丄壓恾偺傛偆偵偆偢傑偒忬偵抲偄偰偄偒傑偡丅偙偺偲偒丄師偺栤偄偵摎偊側偝偄丅
丂丂丂丂丂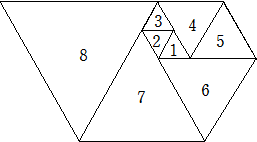
乮侾乯丂侾俈斣栚偺惓嶰妏宍傪抲偄偨偲偒丄偱偒傞恾宍偺廃偺挿偝偼壗們倣偱偡偐丅
乮俀乯丂侾俆斣栚偺惓嶰妏宍傪抲偄偨偲偒丄偱偒傞恾宍偺柺愊偼丄侾斣栚偺惓嶰妏宍偺
丂丂丂柺愊偺壗攞偱偡偐丅
乮夝乯乮侾乯丂俀侾亄俀俉亄俁俈亄係俋亄俇俆亄俇俆亖俀俇俆乮們倣乯
丂乮俀乯丂俁亄係亄係亄俋亄侾俇亄俀俆亄係俋亄俉侾亄侾係係亄俀俆俇亄係係侾亄俈俉係亄侾俁俇俋
丂丂丂亖俁侾俉俆乮攞乯
乮僐儊儞僩乯丂悢楍揑偵峫偊傛偆偲偟傑偟偨偑丄幚嵺偵奊傪昤偄偰悢偊偨曽偑懍偦偆偩偭偨偺偱丄
丂丂丂丂丂丂揇廘偔媮傔偰傒傑偟偨丅
丂侾斣栚偺惓嶰妏宍偐傜巒傔偰侾曈偺挿偝偺悢楍偼丄
丂侾丆侾丆侾丆俀丆俀丆俁丆係丆俆丆俈丆俋丆侾俀丆侾俇丆俀侾丆俀俉丆俁俈丆係俋丆俇俆丆丒丒丒
偱偁傞丅偦偺奒嵎悢楍傪挷傋偰傒傞偲丄
丂丂侽丆侽丆侾丆侽丆侾丆侾丆侾丆俀丆俁丆係丆俆丆俈丆俋丆侾俀丆侾俇丆丒丒丒
偲側傞偺偱丄嵟弶偺偄偔偮偐偺崁傪彍偄偰丄壗偲側偔婯懃惈偑尒偊偰偔傞丅
俁丏丂偁傞偍揦偱僠乕僘働乕僉偲僾儕儞傪攦偄傑偡丅偳偪傜傕彮側偔偲傕侾屄偼攦偆偙偲偵
丂丂偟傑偡丅僠乕僘働乕僉偼侾屄俁侽侽墌丄僾儕儞偼侾屄侾俀侽墌偱偡丅抣抜偼徚旓惻傪傆
丂丂偔傫偱偄傑偡丅偙偺偲偒丄師偺栤偄偵摎偊側偝偄丅
乮侾乯丂僠乕僘働乕僉偲僾儕儞傪崌傢偣偰侾俉屄攦偄丄戙嬥偑俁俆侽侽墌埲忋係俆侽侽墌埲壓
丂丂偵側傞傛偆偵偟傑偡丅峫偊傜傟傞屄悢偺慻崌偣傪偡傋偰摎偊側偝偄丅
乮俀乯丂僙乕儖偺婜娫偵偼丄僠乕僘働乕僉偼侾侽屄傪偙偊傞偲丄偙偊偨暘偼傕偲偺抣抜偺
丂丂俆亾堷偒偵側傝傑偡丅僙乕儖婜娫拞偵攦偄暔傪偟丄偦偺戙嬥偑偪傚偆偳俋侽侽侽墌偵
丂丂側傞応崌偺屄悢偺慻崌偣傪偡傋偰摎偊側偝偄丅
乮夝乯乮侾乯丂僠乕僘働乕僉傪倶屄攦偆偲偡傞偲丄僾儕儞偼丄侾俉亅倶屄側偺偱丄戣堄傛傝丄
丂丂俁俆侽侽亝俁侽侽倶亄侾俀侽乮侾俉亅倶乯亝係俆侽侽丂偐傜丄侾俁係侽亝侾俉侽倶亝俀俁係侽
丂丂傛偭偰丄俈丏丒丒丒亝倶亝侾俁丂傛傝丄
丂乮僠乕僘働乕僉丆僾儕儞乯亖乮俉丆侾侽乯丄乮俋丆俋乯丄乮侾侽丆俉乯丄乮侾侾丆俈乯丄乮侾俀丆俇乯丄乮侾俁丆俆乯
乮俀乯丂僠乕僘働乕僉傪倶屄丄僾儕儞傪倷屄攦偆偲偡傞丅侾亝倶亝侾侽偺偲偒丄戣堄傛傝丄倶偑婏悢偼
丂丂婲偙傝偊側偄偺偱丄丂倶亖俀丄係丄俇丄俉丄侾侽
丂丂偙偺偲偒丄偦傟偧傟丂倷亖乮俋侽侽侽亅俁侽侽倶乯/侾俀侽亖俈侽丄俇俆丄俇侽丄俆俆丄俆侽
丂丂丂倶亜侾侽丂偺偲偒丄丂丂俁侽侽亊侾侽亄俀俉俆乮倶亅侾侽乯亄侾俀侽倷亖俋侽侽侽
丂丂丂丂偡側傢偪丄丂俀俉俆倶亄侾俀侽倷亖俉俉俆侽丂傛傝丄丂侾俋倶亄俉倷亖俆俋侽
丂丂丂偙偺偲偒丄丂侾俋亊乮亅俀乯亄俉亊俆亖俀丂傛傝丄丂侾俋亊乮亅俆俋侽乯亄俉亊侾係俈俆亖俆俋侽
丂丂丂傛偭偰丄丂侾俋乮倶亄俆俋侽乯亖俉乮侾係俈俆亅倷乯
丂丂丂侾俋偲俉偼屳偄偵慺側偺偱丄丂倶亄俆俋侽亖俉倠丂丄丂侾係俈俆亅倷亖侾俋倠
丂丂丂丂倶亖俉倠亅俆俋侽亜侾侽丂傛傝丄丂倠亜俈俆丂丂傛偭偰丄倠亞俈俇
丂丂丂丂倷亖侾係俈俆亅侾俋倠亞侾丂傛傝丄丂倠亝俈俈丏丒丒丒
丂丂丂埲忋偐傜丄丂倠亖俈俇丄俈俈
丂丂丂丂倠亖俈俇丂偺偲偒丄丂倶亖俇侽俉亅俆俋侽亖侾俉丂丄倷亖侾係俈俆亅侾係係係亖俁侾
丂丂丂丂倠亖俈俈丂偺偲偒丄丂倶亖俇侾俇亅俆俋侽亖俀俇丂丄倷亖侾係俈俆亅侾係俇俁亖侾俀
丂埲忋偐傜丄
乮僠乕僘働乕僉丆僾儕儞乯亖乮俀丆俈侽乯丄乮係丆俇俆乯丄乮俇丆俇侽乯丄乮俉丆俆俆乯丄乮侾侽丆俆侽乯丄乮侾俉丆俁侾乯丄乮俀俇丆侾俀乯
乮捛婰乯丂暯惉俀俉擭俀寧俆擔乮嬥乯晅偗挬擔怴暦挬姧偵暯惉俀俉擭搙嶗堻拞妛擖帋栤戣偑宖
丂丂丂丂嵹偝傟偨丅嫽枴偁傞栤戣偑偁偭偨偺偱挧愴偟偰傒偨丅乮堦晹夵戣乯
丂摍娫妘偵乮侾乯偐傜乮俋乯傑偱偺斣崋偑偮偄偨摴楬偑偁傞丅俁恖俙丄俛丄俠偺曕偔懍偝丄憱
傞懍偝丄帺揮幵偺懍偝偼偦傟偧傟摍偟偄偲偡傞偲偒丄師偺栤偄偵摎偊傛丅
丂俀偮偺娫妘偺娫傪俈俆昩偱曕偒丄係侽昩偱憱傝丄俀俆昩偱帺揮幵傪憱傜偣傞傕偺偲偡傞丅
乮僀乯丂俙偼侾侽帪偵抧揰乮侾乯傪曕偄偰弌敪偟丄搑拞偺抧揰偐傜憱偭偰抧揰乮俋乯偵払偟偨丅
丂丂抧揰乮俋乯偱偼侾暘媥傒丄帺揮幵偱抧揰乮侾乯偵栠偭偨丅俛偼侾侽帪偵抧揰乮侾乯傪帺揮
丂丂幵偱弌敪偟丄抧揰乮俆乯偵拝偄偰係暘係俆昩媥傒丄偦偺屻偼曕偄偰丄抧揰乮侾乯偵栠偭
丂丂偨丅俀恖偑摨帪崗偵抧揰乮侾乯偵栠偭偨偲偒丄俙偼偳偺抧揰偐傜憱傝巒傔偨偐丅
乮儘乯丂乮僀乯偺偲偒丄俠偼侾侽帪偵抧揰乮俉乯偐傜帺揮幵偱抧揰乮侾乯偵岦偐偭偨丅抧揰乮侾乯
丂丂偵拝偔搑拞偱丄俙丄俛偲偡傟堘偭偨丅俛偲偡傟堘偭偨屻丄壗昩屻偵俙偲偡傟堘偭偨偐丅
丂挿暥傪撉傫偱摢偑僋儔僋儔偟偰偔傞偑丄摦偒傪師偺傛偆偵恾帵偡傞偲暘偐傝傗偡偄丅
丂丂
乮夝乯乮僀乯丂抧揰乮倶亄侾乯偐傜憱傝巒傔偨偲偡傞偲丄
丂丂丂丂丂俈俆倶亄係侽乮俉亅倶乯亄俇侽亄俀俆丒俉亖係丒俀俆亄俀俉俆亄俈俆丒係
丂丂丂偡側傢偪丄丂俁俆倶亄俆俉侽亖俇俉俆丂傛傝丄丂俁俆倶亖侾侽俆丂丂傛偭偰丄倶亖俁
丂丂丂偟偨偑偭偰丄俙偼抧揰乮係乯傛傝憱傝巒傔偨丅
乮儘乯丂俛偲偡傟堘偆傑偱偺帪娫傪倶偲偍偔偲丄
丂丂丂丂乮係/侾侽侽乯倶亖亅乮俈/侾俈俆乯倶亄俈丂傛傝丄倶亖侾俈俆/俀
丂丂俙偲偡傟堘偆傑偱偺帪娫傪倶偲偍偔偲丄亅乮俈/侾俈俆乯倶亄俈亖乮俁/俀俀俆乯倶丂傛傝丄丂倶亖俆俀俆/係
丂丂傛偭偰丄丂俆俀俆/係亅侾俈俆/俀亖侾俈俆/係丂傛傝丄丂係俁丏俈俆昩屻偵俙偲偡傟堘偆丅
乮捛婰乯丂暯惉俀俋擭俀寧係擔乮搚乯晅偗挬擔怴暦挬姧偵暯惉俀俋擭搙奐惉拞妛擖帋栤戣偑宖
丂丂丂丂嵹偝傟偨丅攚屻偵栘晹愭惗偺婥攝傪姶偠偮偮挧愴偟偰傒偨丅乮堦晹夵戣乯
侾丏丂師偺奺栤偄偵摎偊側偝偄丅
乮侾乯丂師偺乮丂乯偵偼摨偠悢偑擖傝傑偡丅偦偺悢傪媮傔側偝偄丅
丂丂丂乮俁俆/俁乯亊乮乮丂乯亊侾丏係亄乮丂乯亐乮侾/俀乯亄俀侽乯亐乮俈/俇侽乯亖俀侽侾俈
乮俀乯丂侾偐傜俀侽侾俈傑偱偺惍悢偺偆偪丄俁偱傕係偱傕妱傝愗傟側偄傕偺傪峫偊傑偡丅偦偺
丂丂丂偆偪丄俀偺攞悢偲俆偺攞悢偼偦傟偧傟壗屄偁傝傑偡偐丅
丂壗傟傕摉俫俹偺乽僷僘儖俀侽侾俈乿偵椶暿偝傟偦偆側栤戣偱柺敀偦偆両
乮夝乯乮侾乯丂傑偢丄乮丂乯亊侾丏係亄乮丂乯亊俀亄俀侽亖俀侽侾俈/侾侽侽丂傛傝丄乮丂乯亊俁丏係亖侾俈/侾侽侽
丂丂丂丂丂丂傛偭偰丄丂乮丂乯亖侾/俀侽
乮俀乯丂侾偐傜俀侽侾俈傑偱偺惍悢偺偆偪丄俀偺攞悢偼慡晹偱丄侾侽侽俉屄偁傞丅偙偺拞偐傜丄俁傑偨
丂丂偼係偱妱傝愗傟傞傕偺傪彍偗偽傛偄丅
丂俀丒侾丄俀丒俀丄俀丒俁丄丒丒丒丒丒丒丄俀丒侾侽侽俉丂傛傝丄侾丄俀丄俁丄丒丒丒丒丒丒丒丄侾侽侽俉偱丄俀傑偨偼俁傑偨
偼係偱妱傝愗傟傞傕偺偼丄丂俆侽係亄俁俁俇亄俀俆俀亅侾俇俉亅俉係亅俀俆俀亄俉係亖俇俈俀乮屄乯
丂傛偭偰丄忦審傪枮偨偡俀偺攞悢偼丄丂侾侽侽俉亅俇俈俀亖俁俁俇乮屄乯丂偁傞丅
丂摨條偵偟偰丄侾偐傜俀侽侾俈傑偱偺惍悢偺偆偪丄俆偺攞悢偼慡晹偱丄係侽俁屄偁傞丅偙偺拞偐傜丄
俁傑偨偼係偱妱傝愗傟傞傕偺傪彍偗偽傛偄丅
丂俆丒侾丄俆丒俀丄俆丒俁丄丒丒丒丒丒丒丄俆丒係侽俁丂傛傝丄侾丄俀丄俁丄丒丒丒丒丒丒丒丄係侽俁偱丄俁傑偨偼係偱妱傝愗
傟傞傕偺偼丄丂侾俁係亄侾侽侽亅俁俁亖俀侽侾乮屄乯
丂傛偭偰丄忦審傪枮偨偡俆偺攞悢偼丄丂係侽俁亅俀侽侾亖俀侽俀乮屄乯丂偁傞丅
乮僐儊儞僩乯丂乮侾乯偼晛捠儗儀儖偵偟偰傕乮俀乯偼乽彫妛惗偵屄悢掕棟丠乿偲巚偆偔傜偄擄栤偱偡偹丅
丂丂丂丂丂丂偦傟偲傕懠偵彫妛惗儗儀儖偺夝朄偑偁傞偺偐側丠
俀丏偼栤戣暥偑挿偡偓偰僷僗両
俁丏丂師偺奺栤偄偵摎偊側偝偄丅
乮侾乯丂壓偺恾偵偍偄偰丄巐妏宍俙俛俠俢偲巐妏宍俙俛俤俥偼偳偪傜傕挿曽宍偱丄俁偮偺捈
丂丂慄俙俧丄俛俢丄俤俥偑侾揰俫偱岎傢偭偰偄傑偡丅俧俤偺挿偝偑侾們倣丄俢俥偺挿偝偑俋們倣丄
丂丂俙俥偺挿偝偑倶 cm偺偲偒丄倶 偺抣傪媮傔側偝偄丅
丂丂丂丂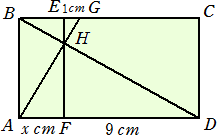
乮俀乯丂俙抧揰偲俛抧揰偺娫偵堦杮摴偑偁傝傑偡丅垻晹孨偼偙偺摴傪俙抧揰偐傜俛抧揰
丂丂傊岦偐偭偰暘懍俆侽倣偱恑傒傑偡丅攏応孨傕偙偺摴傪俛抧揰偐傜俙抧揰傊岦偐偭偰
丂丂堦掕偺懍偝偱恑傒傑偡丅擇恖偼摨帪偵弌敪偟丄俛抧揰偐傜俀俆侽倣棧傟偨抧揰偱偡
丂丂傟堘偄傑偟偨丅傑偨丄垻晹孨偑俛抧揰偵拝偄偰偐傜係俇暘侾俀昩屻偵丄攏応孨偼俙抧
丂丂揰偵拝偒傑偟偨丅塃偺恾偼丄擇恖偑弌敪偟偰偐傜偺帪娫偲俙抧揰偐傜偺摴偺傝偺娭
丂丂學傪昞偟偰偄傑偡丅擇恖偑弌敪偟偰偐傜偡傟堘偆傑偱偵偐偐偭偨帪娫傪倷暘偲偡傞偲
丂丂偒丄倷偺抣傪媮傔側偝偄丅
丂丂丂丂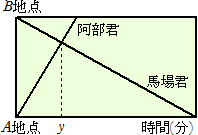
丂偙傟偼丄拞妛擖帋傜偟偄栤戣偱偡偹丅
乮夝乯乮侾乯丂憡帡斾偐傜丄丂倶亖俋/倶丂傛傝丄丂倶亖俁乮們倣乯
乮俀乯丂垻晹孨偑俛抧揰偵摓拝偡傞偺偼丄偡傟堘偭偰偐傜丄丂俀俆侽亐俆侽亖俆乮暘屻乯丅
丂丂傛偭偰丄乮侾乯偲摨條偵峫偊偰丄丂倷亖乮係俇丏俀亄俆乯亊乮俆/倷乯丂偐傜丄丂倷2亖俀俆俇
丂丂偟偨偑偭偰丄丂倷亖侾俇乮暘乯
乮僐儊儞僩乯丂彫妛惗偵暯曽崻偼柍杁偐側丠堘偆夝朄偑偁傞偺偐傕丅
係丏丂掙柺偑AB亖係們倣丄俛俠亖俁們倣丄俠俙亖俆們倣丄佢俙俛俠偺戝偒偝偑俋侽亱偺嶰妏宍
丂丂偱偁傝丄懁柺偑偡傋偰挿曽宍偺摟柧側嶰妏拰ABC-DEF偺僈儔僗偱偱偒偨梕婍偑偁
丂丂傝傑偡丅偙偺梕婍偵偼悈傪擖傟傞偙偲偑偱偒丄偳偺傛偆側岦偒偵抲偄偰傕悈偼楻傟側
丂丂偄傕偺偲偟傑偡丅傑偨丄梕婍偺僈儔僗偺岤偝偼峫偊傑偣傫丅
丂丂丂丂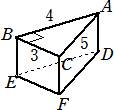
丂丂丂傑偢丄偙偺梕婍偵彮偟悈傪擖傟偨偲偙傠丄柺DEF傪壓偵偟偰悈暯側彴偵抲偄偨偲偒
丂丂偲丄柺BCFE傪壓偵偟偰悈暯側彴偵抲偄偨偲偒偲偱丄梕婍偺壓偺柺偐傜悈柺傑偱偺崅
丂丂偝偑摍偟偔側傝傑偟偨丅
丂丂丂丂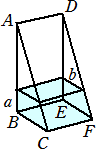
丂丂丂師偵丄偙偺梕婍偵丄偙傟傑偱擖偭偰偄偨検偺俆/係攞偺悈傪偝傜偵捛壛偟偨偲偙傠丄
丂丂柺DEF傪壓偵偟偰悈暯側彴偵抲偄偨偲偒偲丄柺ABED傪壓偵偟偰悈暯側彴偵抲偄偨
丂丂偲偒偲偱丄梕婍偺壓偺柺偐傜悈柺傑偱偺崅偝偑摍偟偔側傝傑偟偨丅
丂丂丂丂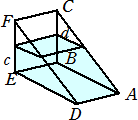
丂丂丂師偺栤偄偵摎偊側偝偄丅
乮侾乯丂挿偝 們 偼挿偝 倎 偺壗攞偱偡偐丅
乮俀乯丂挿偝 倓 偼丄挿偝 倐 傛傝壗們倣挿偄偱偡偐丄傑偨偼丄抁偄偱偡偐丅
乮俁乯丂挿偝 倎 偼壗們倣偱偡偐丅
乮係乯丂BE偺挿偝偼壗們倣偱偡偐丅
乮俆乯丂
丂丂丂丂
丂丂偺忬懺偺偁偲丄偙偺梕婍偵悈傪偝傜偵捛壛偟偨偲偙傠丄柺DEF傪壓偵偟偰悈暯側彴偵
丂丂抲偄偨偲偒偲丄柺ACFD傪壓偵偟偰悈暯側彴偵抲偄偨偲偒偲偱丄梕婍偺壓偺柺偐傜悈
丂丂柺傑偱偺崅偝偑摍偟偔側傝傑偟偨丅偙偺偲偒丄摍偟偄悈柺偺崅偝偼壗們倣偱偡偐丅
乮夝乯乮侾乯丂嵟弶偵悈傪擖傟偰柺DEF傪壓偵偟偰悈暯側彴偵抲偄偨偲偒偺悈柺偺崅偝傪倛偲偍
丂丂丂丂丂偔偲丄戣堄傛傝丄丂倛亖倎丂偱偁傞丅
丂丂丂丂傑偨丄偙偺梕婍偵丄偙傟傑偱擖偭偰偄偨検偺俆/係攞偺悈傪偝傜偵捛壛偟偨偺偱崅偝偼丄
丂丂丂丂俋倛/係偱丄戣堄傛傝丄丂俋倛/係亖們丂偱偁傞丅
丂丂丂丂傛偭偰丄丂們亖乮俋/係乯倎丂偲側傝丄挿偝 們 偼挿偝 倎 偺俋/係攞偱偁傞丅
乮俀乯丂仮俙俛俠偺柺愊偼丄俇們倣2偱丄俛俤亖倶 偲偍偔偲丄戣堄傛傝丄丂俇倛亖乮俁亄倐乯倎倶/俀
丂丂丂傑偨丄丂俇倛亊乮俋/係乯亖乮係亄倓乯們倶/俀亖乮係亄倓乯亊乮俋/係乯倎倶/俀丂傛傝丄
丂丂丂丂丂丂俇倛亖乮係亄倓乯倎倶/俀丂側偺偱丄丂乮俁亄倐乯倎倶/俀亖乮係亄倓乯倎倶/俀
丂丂丂傛偭偰丄丂俁亄倐亖係亄倓丂偲側傝丄丂倓亅倐亖亅侾
丂丂丂偟偨偑偭偰丄挿偝 倓 偼丄挿偝 倐 傛傝 侾們倣抁偄丅
乮俁乯丂係亅倎 丗 係亖倐 丗 俁丂傛傝丄丂倐亖俁乮係亅倎乯/係
丂丂摨條偵偟偰丄丂俁亅們 丗 俁亖倓 丗 係丂傛傝丄丂倓亖係乮俁亅們乯/俁亖係亅俁倎
丂乮俀乯傛傝丄丂係亅俁倎亅俁乮係亅倎乯/係亖亅侾丂側偺偱丄丂倎亖俉/俋乮們倣乯
乮係乯丂乮俁乯傛傝丄丂們亖俀丄倐亖俈/俁丄倓亖係/俁丂偱丄丂倛亖俉/俋丂偲側傞偺偱丄
丂丂丂俇倛亖乮俁亄倐乯倎倶/俀丂偵戙擖偟偰丄丂倶亖俋/係乮們倣乯
乮俆乯丂梕婍偵悈傪偝傜偵捛壛偟偰丄柺DEF傪壓偵偟偰悈暯側彴偵抲偄偨偲偒偺悈柺偺崅偝傪俫
丂丂偲偟丄柺ACFD傪壓偵偟偰悈暯側彴偵抲偄偨偲偒偺懁柺偺戜宍偺忋掙偺挿偝傪倕偲偍偔偲丄
丂丂戣堄傛傝丄
丂丂丂丂丂丂丂丂丂俇俫亖乮俆亄倕乯俫亊乮俋/係乯/俀丂側偺偱丄丂倕亖侾/俁
丂丂丂偙偺偲偒丄仮俙俛俠偺俙俠傪掙曈偲偡傞崅偝倷偼丄丂俆倷/俀亖俇丂傛傝丄丂倷亖侾俀/俆丂側偺偱丄
丂丂丂丂侾俀/俆 丗 俆亖乮侾俀/俆亅俫乯 丗 侾/俁丂偑惉傝棫偮丅
丂丂丂偙傟傪夝偄偰丄丂俫亖俆俇/俀俆乮們倣乯丂偲側傞丅丂丂乮廔乯
乮捛婰乯丂暯惉俀俋擭俀寧俆擔乮擔乯晅偗挬擔怴暦挬姧偵暯惉俀俋擭搙嶗堻拞妛擖帋栤戣偑宖
丂丂丂丂嵹偝傟偨丅柺敀偦偆側偺偱挧愴偟偰傒偨丅乮堦晹夵戣乯
侾丏丂師偺乮丂丂乯偵偁偰偼傑傞悢傪摎偊側偝偄丅
乮侾乯嘆丂乷侾丏侽係亐俋亊乮侾俀亅俆亅係/俈乯亅侾俁/係俀乸亊乮俀亄俀俁/俀俇乯亖乮丂丂乯
丂丂嘇丂乷俈亄俇/侾侾亅乮係亄侾/侾俇乯亐俇丏俉俈俆乸亐乷侾俆亅乮乮丂丂乯亄俆亄侾/俁乯乸亖俇亄俁/係
乮俀乯丂侽偐傜俋傑偱偺侾偗偨偺悢帤侾侽屄偐傜丄堎側傞俀屄偺悢帤傪慖傃傑偡丅偦偺俀屄
丂丂丂偺悢帤傪偳偪傜傕侾夞埲忋巊偭偰係屄傪暲傋偨悢傪嶌傝傑偡丅偨偩偟丄侽傪巊偆偲偒
丂丂丂偼丄偨偲偊偽丄侽侽俁侽偼俁侽丄侽侾侽侾偼侾侽侾偲峫偊傞偙偲偲偟傑偡丅
丂嘆丂偙偺傛偆偵偟偰偱偒傞悢偼慡晹偱乮丂丂乯屄偁傝傑偡丅
丂嘇丂俀侽俀侽偼彫偝偄曽偐傜悢偊偰乮丂丂乯斣栚偺悢偱偡丅
丂嘊丂戝偒偄曽偐傜悢偊偰俋俀斣栚偺悢偼乮丂丂乯偱偡丅
乮夝乯乮侾乯嘆丂乷侾丏侽係亐俋亊乮侾俀亅俆亅係/俈乯亅侾俁/係俀乸亊乮俀亄俀俁/俀俇乯
丂丂丂丂丂丂亖乮侾丏侽係/俋乯亊乮係俆/俈乯亊乮俈俆/俀俇乯亅乮侾俁/係俀乯亊乮俈俆/俀俇乯
丂丂丂丂丂丂亖侾俆/俈亅俈俆/俉係
丂丂丂丂丂丂亖侾侽俆/俉係
丂丂丂丂丂丂亖俆/係
丂嘇丂乷俈亄俇/侾侾亅乮係亄侾/侾俇乯亐俇丏俉俈俆乸亐乷侾俆亅乮乮丂丂乯亄俆亄侾/俁乯乸亖俇亄俁/係
丂丂丂丂乮俉俁/侾侾乯亅乮侾俁/俀俀乯亖乮俀俈/係乯乷乮俀俋/俁乯亅乮丂丂乯乸
丂丂丂丂乮侾俆俁/俀俀乯亊乮係/俀俈乯亖乮俀俋/俁乯亅乮丂丂乯
丂丂丂丂乮丂丂乯亖乮俀俋/俁乯亅乮俁係/俁俁乯亖俀俉俆/俁俁亖俋俆/侾侾
乮俀乯嘆丂10俠2亊乮係両/俁両亄係両/乮俀両俀両乯亄係両/俁両乯亖係俆亊侾係亖俇俁侽乮屄乯
丂嘇丂侽***丂偺僞僀僾偼丄丂俋亊俁亄俋亊俁亄俋亖俇俁
丂丂丂侾***丂偺僞僀僾偼丄丂俋亊俁亄俋亊俁亄俋亖俇俁
丂丂丂俀侽侽侽丄俀侽侽俀丂偺師偑俀侽俀侽
丂丂丂傛傝丄丂俇俁亄俇俁亄俀亄侾亖侾俀俋乮斣栚乯
丂嘊丂俋***丂偺僞僀僾偼丄丂俋亄俋亊俁亄俋亊俁亖俇俁乮屄乯丂側偺偱丄俋俀斣栚偺悢偼丄俉***
丂丂丂偺僞僀僾丅
丂丂丂俉俋**丂偺僞僀僾偼丄丂係捠傝
丂丂丂俉俉**丂偺僞僀僾偼丄丂俋亄俋亊俀亖俀俈捠傝丂偙傟偱丄俋係屄栚
丂丂丂丂俋俀斣栚偺悢偼丄俉俉**丂偺僞僀僾偱彫偝偄曽偐傜俁斣栚偺悢側偺偱丄
丂丂丂俉俉侽侽丄俉俉侽俉丄俉俉侾侾丄俉俉侾俉丄俉俉俀俀丄俉俉俀俉丄俉俉俁俁丄丒丒丒丂偐傜丄摎偊偼丄俉俉侾侾
俀丏丂壓偺恾偼丄俙俢亖俢俫亖侾俇們倣丄俧俫亖侾俀們倣偺捈曽懱俙俛俠俢-俤俥俧俫偱丄
丂丂俙俥亖俀侽們倣偱偡丅俀偮偺摦偔揰俹偲俻偑摨帪偵弌敪偟偰丄枅昩俀們倣偺懍偝偱揰俹
丂丂偼挿曽宍俙俢俧俥偺廃忋傪丄揰俻偼嶰妏宍俠俢俧偺廃忋傪師偺傛偆偵摦偒傑偡丅
丂揰俹丗俙仺俢仺俧仺俥仺俙仺俢仺俧仺丒丒丒
丂揰俻丗俧仺俢仺俠仺俧仺俢仺丒丒丒
丂丂丂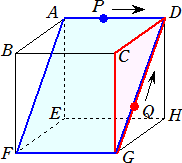
乮侾乯丂俀揰俹丄俻偑弶傔偰弌夛偆偺偼丄俀揰偑弌敪偟偰偐傜壗昩屻偱偡偐丅
乮俀乯丂俀揰俹丄俻偑係夞栚偵弌夛偆偺偼丄俀揰偑弌敪偟偰偐傜壗暘壗昩屻偱偡偐丅
乮夝乯丂揰俹偑挿曽宍俙俢俧俥傪堦廃偡傞偺偵梫偡傞帪娫偼丄丂俉仺侾侽仺俉仺侾侽丂偺寁俁俇昩
丂丂丂揰俻偑嶰妏宍俠俢俧傪堦廃偡傞偺偵梫偡傞帪娫偼丄丂侾侽仺俇仺俉丂偺寁俀係昩
乮侾乯丂俀揰俹丄俻偑弶傔偰弌夛偆偺偼丄慄暘俢俧忋偱丄偦傟偑弌敪偐傜 倶 昩屻偲偡傞偲丄
丂丂丂俀倶亖俁俇亅俀倶丂偐傜丄丂倶亖俋丂丂傛偭偰丄俀揰偑弌敪偟偰偐傜俋昩屻偵弶傔偰弌夛偆丅
乮俀乯丂俀揰俹丄俻偑弌夛偆偺偼慄暘俢俧忋偱偁傞丅揰俹偑慄暘俢俧忋偵偁傞帪娫偼丄弌敪偐傜丄
丂俉乣侾俉丄係係乣俆係丄俉侽乣俋侽丄侾侾俇乣侾俀俇丄侾俆俀乣侾俇俀丄丒丒丒
丂丂揰俻偑慄暘俢俧忋偵偁傞帪娫偼丄弌敪偐傜丄
丂侽乣侾侽丄俀係乣俁係丄係俉乣俆俉丄俈俀乣俉俀丄俋俇乣侾侽俇丄侾俀侽乣侾俁侽丄侾係係乣侾俆係丄丒丒丒
丂傛偭偰丄俀揰俹丄俻偑係夞栚偵弌夛偆偺偼丄揰俹偑揰俢傪侾侾俇昩屻偵弌敪偟丄揰俻偑揰俧傪
侾俀侽昩屻偵弌敪偟偰慄暘俢俧忋偱弌夛偆偺偱丄丂乮俀侽亅俀亊係乯亐俀亐俀亖俁
丂傛偭偰丄俀揰偑弌敪偟偰偐傜丄侾俀侽亄俁亖侾俀俁乮昩屻乯丂偡側傢偪丄俀暘俁昩屻丂偵係夞栚偺
弌夛偄偑偁傞丅丂丂乮廔乯
乮僐儊儞僩乯丂偙偆偄偆栤戣偭偰丄偄偐偵傕嶼悢偭傐偔偰岲偒偱偡偹丅乮侾乯偱曽掱幃傪棫偰偰偟傑
丂丂丂丂丂丂偄傑偟偨偑丄棫偰側偔偰傕丂俁俇亐俀亐俀亖俋乮昩屻乯丂偲偟偰傕丄捈偖暘偐傝傑偡丅
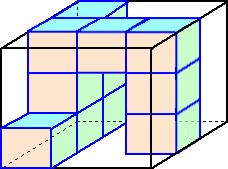
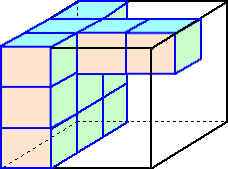
俁丏丂侾曈偺挿偝偑偦傟偧傟俁們倣丄侾俀們倣丄俀侾們倣偺惓曽宍傪掙柺偲偡傞捈曽懱偐傜
丂丂忋偺柺傪庢傝彍偄偰偱偒偨俁偮偺悈憛俙丄俛丄俠傪廳偹偰乮俠偺拞偵俛丄俛偺拞偵俙乯
丂丂掙柺傪屌掕偟偨梕婍偑偁傞丅偙偺梕婍傪悈暯側彴偺忋偵抲偒丄悈憛俙丄俛丄偺偦傟
丂丂偧傟偵丄幹岥倎丄倐丄們偐傜枅昩堦掕偺検偺悈傪摨帪偵擖傟巒傔丄慡偰偺悈憛偑悈
丂丂偱枮偨偝傟傞傑偱俁偮偺幹岥偐傜悈傪擖傟懕偗傑偟偨丅偨偩偟丄梕婍偺岤偝偼峫偊
丂丂側偄傕偺偲偟傑偡丅
乮侾乯丂壓偺恾偼丄悈傪擖傟巒傔偰偐傜梕婍偑悈偱枮偨偝傟傞傑偱偺帪娫偲悈柺偺崅偝
丂丂丂偺娭學傪昞偟偨僌儔僼偱偡丅悈傪擖傟巒傔偰偐傜乮傾乯昩屻傑偱偺悈憛俛偺悈柺偑
丂丂丂忋徃偡傞懍偝偑枅昩侾/俀俈們倣丄乮僂乯偑侾俉俋偱偁傞偲偒丄師偺嘆丄嘇傪媮傔側偝偄丅
丂丂嘆丂侾偮偺幹岥偐傜侾昩娫偵弌傞悈偺検
丂丂嘇丂悈憛俠偺崅偝
丂丂丂丂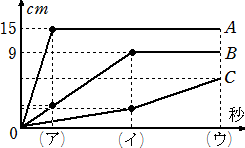
乮俀乯丂偙偺梕婍傪嬻偵偟偰丄嵞傃俁偮偺幹岥偐傜枅昩堦掕偺検偺悈傪擖傟傑偟偨丅慡
丂丂丂偰偺悈憛偑悈偱枮偨偝傟傞傑偱偵俀暘偐偐偭偨偲偒丄侾偮偺幹岥偐傜侾昩娫偵弌
丂丂丂傞悈偺検傪媮傔側偝偄丅
乮夝乯乮侾乯嘆丂悈憛俛偺拞偵悈憛俙偑偁傞偺偱丄悈憛俛偺幚嵺偺掙柺愊偼丄
丂丂丂丂丂丂丂丂侾俀亊侾俀亅俁亊俁亖侾俁俆乮們倣2乯
丂丂丂丂丂丂丂傛偭偰丄侾偮偺幹岥偐傜侾昩娫偵弌傞悈偺検偼丄丂侾俁俆亊侾/俀俈亖俆乮們倣3乯
嘇丂悈憛俙偑悈偱枮偨偝傟傞偺偵梫偡傞帪娫偼丄丂俁亊俁亊侾俆亐俆亖俀俈乮昩乯
丂丂悈憛俛偑悈偱枮偨偝傟傞偺偵梫偡傞帪娫偼丄
丂丂丂丂乮侾俁俆亊俋亅俆亊俀俈乯亐侾侽亄俀俈亖侾俁俆乮昩乯
丂丂悈憛俠偺崅偝傪倛乮們倣乯偲偡傞偲丄
丂丂丂丂乮俀侾亊俀侾亅侾俀亊侾俀乯亊倛亅俆亊侾俁俆亖侾俆亊乮侾俉俋亅侾俁俆乯
丂丂偡側傢偪丄丂俀俋俈倛亖侾係俉俆丂傛傝丄丂倛亖俆乮們倣乯
乮俀乯丂侾偮偺幹岥偐傜侾昩娫偵弌傞悈偺検傪 倶 們倣3偲偡傞偲丄
丂丂悈憛俙偑悈偱枮偨偝傟傞偺偵梫偡傞帪娫偼丄丂俁亊俁亊侾俆亐倶亖侾俁俆/倶乮昩乯
丂丂悈憛俛偑悈偱枮偨偝傟傞偺偵梫偡傞帪娫偼丄
丂丂丂丂乮侾俁俆亊俋亅倶亊乮侾俁俆/倶乯乯亐俀倶亄侾俁俆/倶亖俇俈俆/倶乮昩乯
丂丂悈憛俠偺崅偝偼俆們倣側偺偱丄
丂丂丂丂乮俀侾亊俀侾亅侾俀亊侾俀乯亊俆亅倶亊乮俇俈俆/倶乯亖俁倶亊乮侾俀侽亅俇俈俆/倶乯
丂丂偡側傢偪丄丂侾係俉俆亅俇俈俆亖俁俇侽倶亅俀侽俀俆丂傛傝丄丂俁俇侽倶亖俀俉俁俆
丂丂傛偭偰丄侾偮偺幹岥偐傜侾昩娫偵弌傞悈偺検偼丄俇俁/俉 們倣3 偲側傞丅丂丂乮廔乯
乮僐儊儞僩乯丂傛偔峫偊傜傟偨栤戣偱偡偹両夝偄偰妝偟偐偭偨偱偡丅
係丏丂棫懱侾乮掙柺偑敿宎俇們倣偺捈墌悗乮偨偩偟丄曣慄偺挿偝俀俆們倣乯乯丄棫懱俀乮掙柺
丂丂偑敿宎俁們倣丄崅偝俀侽們倣偺捈墌拰乯丄棫懱俁乮掙柺偑敿宎係們倣丄崅偝侾俆們倣偺捈
丂丂墌拰偐傜掙柺偑敿宎俀們倣丄崅偝侾俆們倣偺捈墌拰傪偔傝偸偄偨傕偺乯偺偦傟偧傟偑
丂丂侾屄埲忋偁傝傑偡丅
丂丂丂棫懱侾偺壓偺柺偼愒丄棫懱俀偺忋壓偺柺偼惵丄棫懱俁偺忋壓偺柺偼墿怓偵揾傜
丂丂傟偰偄偰丄偳偺棫懱傕偦偺懠偺柺偼慡偰敀偔揾傜傟偰偄傑偡丅偙偺偲偒丄師偺栤偄
丂丂偵摎偊側偝偄丅偨偩偟丄墌廃棪偼丄俁丏侾係偲偟傑偡丅
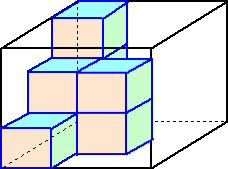
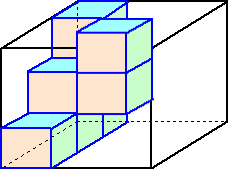
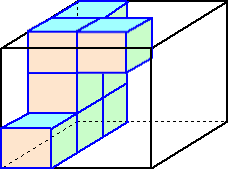
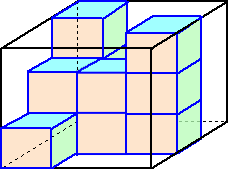
乮侾乯丂棫懱侾丄俀丄俁偺侾屄偢偮偵偮偄偰丄敀偔揾傜傟偰偄傞晹暘偺柺愊偲丄愒丄惵丄墿
丂丂丂怓偵揾傜傟偰偄傞晹暘偺柺愊傪偦傟偧傟媮傔側偝偄丅
乮俀乯丂慡偰偺棫懱偺愒偔揾傜傟偰偄傞晹暘偺柺愊偺崌寁偲丄惵偔揾傜傟偰偄傞晹暘偺
丂丂丂柺愊偺崌寁偲丄墿怓偔揾傜傟偰偄傞晹暘偺柺愊偺崌寁偑偳傟傕摨偠偲偒丄慡偰偺
丂丂丂棫懱偺敀偔揾傜傟偰偄傞晹暘偺柺愊偺崌寁偼嵟傕彮側偔偰壗們倣2偱偡偐丅
乮俁乯丂慡偰偺棫懱偺敀偔揾傜傟偰偄傞晹暘偺柺愊偺崌寁偑俆俇俆俀們倣2偱偁傞偲偒丄棫
丂丂丂懱侾丄俀丄俁偼偦傟偧傟壗屄偢偮偁傝傑偡偐丅峫偊傜傟傞屄悢偺慻傪慡偰摎偊側偝
丂丂丂偄丅偨偩偟丄棫懱侾丄俀丄俁偼偳傟傕堎側傞屄悢偁傞偲偟傑偡丅
乮夝乯乮侾乯丂敀丂棫懱侾丒丒丒俀俆亊俀俆亊俁丏侾係亊乮俀亊俁丏侾係亊俇乯亐乮俀亊俁丏侾係亊俀俆乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖俀俆亊俁丏侾係亊俇亖係俈侾乮們倣2乯
丂丂丂丂丂丂丂丂丂棫懱俀丒丒丒俀亊俁丏侾係亊俁亊俀侽亖俁俈俇丏俉乮們倣2乯
丂丂丂丂丂丂丂丂丂棫懱俁丒丒丒俀亊俁丏侾係亊係亊侾俆亄俀亊俁丏侾係亊俀亊侾俆
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖俀亊俁丏侾係亊俇亊侾俆亖俆俇俆丏俀乮們倣2乯
丂丂丂丂丂丂丂愒丂棫懱侾丒丒丒俇亊俇亊俁丏侾係亖侾侾俁丏侽係乮們倣2乯
丂丂丂丂丂丂丂惵丂棫懱俀丒丒丒俁亊俁亊俁丏侾係亊俀亖俆俇丏俆俀乮們倣2乯
丂丂丂丂丂丂丂墿丂棫懱俁丒丒丒俀亊乮係亊係亊俁丏侾係亅俀亊俀亊俁丏侾係乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖俀亊侾俀亊俁丏侾係亖俈俆丏俁俇乮們倣2乯
乮俀乯丂乮侾乯傛傝丄棫懱侾丄棫懱俀丄棫懱俁偺屄悢偺斾偼丄丂俀 丗 係 丗 俁丂側偺偱丄媮傔傞柺愊偼丄
丂丂彮側偔偲傕丂係俈侾亊俀亄俁俈俇丏俉亊係亄俆俇俆丏俀亊俁亖係侾係係丏俉乮們倣2乯
乮俁乯丂戣堄傛傝丄丂係俈侾亊倶亄俁俈俇丏俉亊倷亄俆俇俆丏俀亊倸亖俆俇俆俀
丂丂俆俇俆俀偼係俈侾偱妱傝愗傟傞偑丄棫懱俀丄棫懱俁偼侽屄乮摨悢乯偲側傝丄晄揔丅傛偭偰丄棫懱俀丄
丂棫懱俁偼丄侾屄埲忋偁傞丅偙偺偲偒丄丂倶亝侾侽丄倷亝侾俁丄倸亝俋丂偺斖埻偱媮傔傟偽傛偄丅丂丂丂
丂塃曈偺彫悢晹暘偑側偄偺偱丄婲偙傝摼傞慻崌偣偼丄
丂乮倷丆倸乯亖乮俇丆侾乯丄乮俈丆俀乯丄乮俉丆俁乯丄乮俋丆係乯丄乮侾侾丆侾乯丄乮侾俁丆俁乯丄乮侾丆俇乯丄乮俀丆俈乯丄
丂丂丂丂丂丂乮俁丆俉乯丄乮係丆俋乯
丂乮倷丆倸乯亖乮俇丆侾乯偺偲偒丄丂係俈侾亊倶亄俁俈俇丏俉亊俇亄俆俇俆丏俀亊侾亖俆俇俆俀丂傛傝丄
丂丂丂丂丂丂丂丂丂丂丂丂係俈侾亊倶亖俀俉俀俇丂丂偙偺偲偒丄丂倶亖俇丂偲側傝丄晄揔
丂乮倷丆倸乯亖乮俈丆俀乯偺偲偒丄丂係俈侾亊倶亄俁俈俇丏俉亊俈亄俆俇俆丏俀亊俀亖俆俇俆俀
丂丂丂丂丂丂丂丂丂丂丂丂係俈侾亊倶亖侾俉俉係丂丂偙偺偲偒丄丂倶亖係
丂乮倷丆倸乯亖乮俉丆俁乯偺偲偒丄丂係俈侾亊倶亄俁俈俇丏俉亊俉亄俆俇俆丏俀亊俁亖俆俇俆俀
丂丂丂丂丂丂丂丂丂丂丂丂係俈侾亊倶亖俋係俀丂丂偙偺偲偒丄丂倶亖俀
丂乮倷丆倸乯亖乮俋丆係乯偺偲偒丄丂係俈侾亊倶亄俁俈俇丏俉亊俋亄俆俇俆丏俀亊係亖俆俇俆俀
丂丂丂丂丂丂丂丂丂丂丂丂係俈侾亊倶亖侽丂丂偙偺偲偒丄丂倶亖侽丂偲側傝丄晄揔
丂乮倷丆倸乯亖乮侾侾丆侾乯偺偲偒丄丂係俈侾亊倶亄俁俈俇丏俉亊侾侾亄俆俇俆丏俀亊侾亖俆俇俆俀
丂丂丂丂丂丂丂丂丂丂丂丂係俈侾亊倶亖俋係俀丂丂偙偺偲偒丄丂倶亖俀
丂乮倷丆倸乯亖乮侾俁丆俁乯偺偲偒丄丂係俈侾亊倶亄俁俈俇丏俉亊侾俁亄俆俇俆丏俀亊俁亖俆俇俆俀
丂丂丂丂丂丂丂丂丂丂丂丂係俈侾亊倶亖亅俋係俀丂丂偙偺偲偒丄倶 偼晧悢偲側傝丄晄揔
丂乮倷丆倸乯亖乮侾丆俇乯偺偲偒丄丂係俈侾亊倶亄俁俈俇丏俉亊侾亄俆俇俆丏俀亊俇亖俆俇俆俀
丂丂丂丂丂丂丂丂丂丂丂丂係俈侾亊倶亖侾俉俉係丂丂偙偺偲偒丄丂倶亖係
丂乮倷丆倸乯亖乮俀丆俈乯偺偲偒丄丂係俈侾亊倶亄俁俈俇丏俉亊俀亄俆俇俆丏俀亊俈亖俆俇俆俀
丂丂丂丂丂丂丂丂丂丂丂丂係俈侾亊倶亖俋係俀丂丂偙偺偲偒丄丂倶亖俀丂偲側傝丄晄揔
丂乮倷丆倸乯亖乮俁丆俉乯偺偲偒丄丂係俈侾亊倶亄俁俈俇丏俉亊俁亄俆俇俆丏俀亊俉亖俆俇俆俀
丂丂丂丂丂丂丂丂丂丂丂丂係俈侾亊倶亖侽丂丂偙偺偲偒丄丂倶亖侽丂偲側傝丄晄揔
丂乮倷丆倸乯亖乮係丆俋乯偺偲偒丄丂係俈侾亊倶亄俁俈俇丏俉亊係亄俆俇俆丏俀亊俋亖俆俇俆俀
丂丂丂丂丂丂丂丂丂丂丂丂係俈侾亊倶亖亅俋係俀丂丂偙偺偲偒丄倶 偼晧悢偲側傝丄晄揔
丂埲忋偐傜丄峫偊傜傟傞屄悢偺慻偼丄
丂丂乮倶丆倷丆倸乯亖乮係丆俈丆俀乯丄乮俀丆俉丆俁乯丄乮俀丆侾侾丆侾乯丄乮係丆侾丆俇乯
乮僐儊儞僩乯丂暥復偼挿偄偑丄斾妑揑暯堈側栤戣偲尵偊傞偱偟傚偆丅乮俁乯偼峫偊傜傟傞屄悢偺慻
丂丂丂丂丂丂傪偡傋偰摎偊傞栤戣偱丄偙傟偼彮偟恎峔偊偰偟傑偄傑偡偹両
丂丂搑拞偱寁嶼偟側偑傜婥偯偄偨偺偱偡偑丄係俈侾亊倶亄俁俈俇丏俉亊倷亄俆俇俆丏俀亊倸亖俆俇俆俀
丂偐傜丄椉曈傪娙栺偟偰丄丂俆倶亄係倷亄俇倸亖俇侽丂偲弌棃傞傫偱偡偹丅
乮捛婰乯丂暯惉俁侽擭俀寧係擔乮擔乯晅偗挬擔怴暦挬姧偵暯惉俁侽擭搙嶗堻拞妛擖帋栤戣偑宖
丂丂丂丂嵹偝傟偨丅柺敀偦偆側偺傪僠儑僀僗偟偰挧愴偟偰傒偨丅乮堦晹夵戣乯
嘥丂師偺仩偵偁偰偼傑傞悢丄暥帤傪摎偊側偝偄丅
乮俀乯嘆丂偁傞惍悢値傪俀夞偐偗偰偱偒偨悢傪侾侽偱妱偭偨梋傝傪亙値亜偲昞偡偙偲偵偟傑偡丅
丂丂丂丂偨偲偊偽丄俀亊俀亖係丂側偺偱丄亙俀亜亖係
丂丂丂丂丂丂丂丂丂丂俈亊俈亖係俋丄係俋亐侾侽亖係丂偁傑傝丂俋丂側偺偱丄亙俈亜亖俋丂偱偡丅
丂丂丂丂偙偺偲偒丄侾偐傜侾俀俈傑偱偺惍悢偱丄亙値亜亖係丂偲側傞惍悢値偼仩屄偁傝傑偡丅
丂嘇丂偁傞惍悢値傪俀夞偐偗偰偱偒偨悢傪侾俆偱妱偭偨梋傝傪佱値佲偲昞偡偙偲偵偟傑偡丅
丂丂丂偙偺偲偒丄侾俈傪侾俈夞偐偗偨悢傪倣偲偡傞偲丄佱倣佲亖仩丂偱偡丅
乮夝乯嘆丂戣堄傛傝丄丂値亖侾侽倣亄倠丂偲偍偗傞丅
丂偨偩偟丄倣亖侽丂偺偲偒丄惍悢倠偼丄侾亝倠亝俋丂傪枮偨偡丅倣亖侾俀丂偺偲偒丄惍悢倠偼丄
侽亝倠亝俈丂傪枮偨偡丅偦傟埲奜偺倣乮侾亝倣亝侾侾乯偺偲偒丄惍悢倠偼丄侽亝倠亝俋丂傪枮偨偡丅
丂亙値亜亖倠2亖係丂傪枮偨偡惍悢倠偼丄丂倠亖俀丄俉
丂倠亖俀丂偺偲偒丄揔偡傞倣偼丄丂倣亖侽丄侾丄俀丄丒丒丒丄侾俀丂偺侾俁屄
丂倠亖俉丂偺偲偒丄揔偡傞倣偼丄丂倣亖侽丄侾丄俀丄丒丒丒丄侾侾丂偺侾俀屄
丂丂傛偭偰丄媮傔傞惍悢値偼丄丂侾俁亄侾俀亖俀俆乮屄乯偁傞丅
嘇丂侾俈17亖乮侾俆亄俀乯17佭俀17丂乮倣倧倓丂侾俆乯丂傛傝丄丂乮侾俈17乯2佭俀34丂乮倣倧倓丂侾俆乯
丂丂偙偙偱丄丂俀4佭侾丂乮倣倧倓丂侾俆乯丂側偺偱丄丂俀34亖乮俀4乯8丒俀2佭係丂乮倣倧倓丂侾俆乯
丂丂傛偭偰丄丂佱侾俈17佲亖係丂偲側傞丅
乮僐儊儞僩乯丂嘇偼彮偟戝恖偘側偄夝朄偩偭偨偐側丠
乮俁乯丂係俈恖偺僋儔僗偱丄俆寧俈擔寧梛擔偐傜弌惾斣崋弴偵俈恖偢偮嫵幒憒彍傪偟傑偡丅
丂丂偮傑偁傝丄俆寧俈擔偼侾斣偐傜俈斣丄俆寧俉擔偼俉斣偐傜侾係斣偺恖偑憒彍傪偟傑偡丅擔梛
丂丂擔偲廽嵳擔偼憒彍偼偟傑偣傫丅俆寧俈擔偵憒彍傪偟偨俈恖偑偦傠偭偰師偵憒彍傪偡傞偺
丂丂偼丄仩寧仩擔仩梛擔偱偡丅
乮夝乯丂係俈亖俈亊俇亄俆丄係俈亄俆亖俈亊俈亄俁丄係俈亄俁亖俈亊俈亄侾丄係俈亄侾亖俈亊俇亄俇
丂丂丂係俈亄俇亖俈亊俈亄係丄係俈亄係亖俈亊俈亄俀丄係俈亄俀亖俈亊俈丄係俈亖俈亊俇亄俆丂傛傝丄
丂丂丂俆寧俈擔寧梛擔偐傜悢偊偰丄丂俇亄俈亄俈亄俇亄俈亄俈亄俈亄侾亖係俉乮擔栚乯偵嵞搙摨偠
丂丂斣崋偺恖偑憒彍傪偡傞丅扨弮寁嶼偟偰丄寧梛偐傜搚梛偺廡偼丄慡晹偱丄係俉亐俇亖俉乮廡乯
丂丂偨偩偟丄偙偺婜娫偵廽嵳擔偼側偄偺偱丄嵞搙摨偠斣崋偺恖偑憒彍傪偡傞偺偼丄俉廡栚偺
丂丂嵟廔擔偲側傞丅傛偭偰丄俇寧俁侽擔搚梛擔偲側傞丅
嘨丂侾嶜偁偨傝偺惻崬傒掕壙偑侾侽侽墌偺僲乕僩傪俙揦丄俛揦丄俠揦偱攧偭偰偄傑偡丅攧傝曽偼
師偺捠傝偱偡丅
俙揦丗侾侽嶜傪懇偵偟偰侾懇栚偼侾侽侽侽墌偱斕攧丅俀懇埲忋攦偆偲丄俀懇栚偐傜偼俉侽侽墌偱斕
丂丂丂攧丅侾嶜扨埵偱偼攦偊傑偣傫丅
俛揦丗侾嶜扨埵偱掕壙偱斕攧丅侾侽嶜攦偆枅偵俀嶜偺偍傑偗偑偮偒傑偡丅
俠揦丗侾嶜扨埵偱斕攧丅抣抜偼偡傋偰掕壙偺俉亾堷偒偵側傝傑偡丅 |
丂崱丄俁揦偺偆偪侾揦傑偨偼俀揦偱僲乕僩傪攦偆偙偲偵偟傑偡丅
乮侾乯俀侽嶜偺僲乕僩傪庤偵擖傟傞偨傔偵偼嵟掅偄偔傜偐偐傝傑偡偐丅偨偩偟丄僲乕僩偼梋暘偵
丂丂庤偵擖傟偰傕傛偄傕偺偲偟傑偡丅
乮俀乯係俋侽侽墌埲撪偱庤偵擖傟傞偙偲偑偱偒傞僲乕僩偼嵟戝壗嶜偱偡偐丅
乮俁乯乮俀乯偱媮傔偨嶜悢傪係俋侽侽墌枹枮偱庤偵擖傟傞偲偒丄偦傟偧傟偺揦偱壗嶜偢偮庤偵擖
丂丂傟傟偽傛偄偱偡偐丅峫偊傜傟傞慻傪偡傋偰彂偒側偝偄丅
乮夝乯丂攧傝曽傪傑偲傔傞偲丄
丂丂俙揦丗丂嵟弶偺侾侽嶜偼丄侾侽侽侽墌丅師偺侾侽嶜偼丄俉侽侽墌丅丒丒丒
丂丂俛揦丗丂侾嶜栚偼侾侽侽墌丄俀嶜栚偼丒丒丒丒丒丒丒丒丒丒丄侾侽嶜攦偆偲侾侽侽侽墌偱侾俀嶜庤偵擖傞丅
丂丂俠揦丗丂侾嶜栚偼俋俀墌丄俀嶜栚偼俋俀墌丄丒丒丒丒丒丒丒丒丒丒丅
乮侾乯丂俙揦偺傒偱俀侽嶜丂仺丂侾俉侽侽墌
丂丂丂俛揦偺傒丂仺丂俀侽侽侽墌丂偨偩偟丄俀係嶜庤偵擖傞丅
丂丂丂俠揦偺傒丂仺丂俋俀墌亊俀侽亖侾俉係侽墌
丂丂傛偭偰丄俛揦偱侾侽嶜攦偆偲戙嬥偼侾侽侽侽墌偱侾俀嶜庤偵擖傞丅巆傝偺俉嶜傪俠揦偱攦偆偙偲
丂偵偡傟偽戙嬥偼丄俋俀墌亊俉亖俈俁俇墌丅
丂丂埲忋偐傜丄俀侽嶜偺僲乕僩傪庤偵擖傟傞偨傔偵偼嵟掅侾俈俁俇墌偐偐傞丅
乮俀乯丂俙揦偺傒偩偲丄侾侽侽侽墌亊侾亄俉侽侽墌亊係亖係俀侽侽墌丂偱丄俆侽嶜庤偵擖傞丅
丂丂丂巆傝偺俈侽侽墌暘偱丄俠揦傛傝丄俋俀墌亊俈亖俇係係墌攦偄丄俈嶜庤偵擖傞丅埲忋偱丄俆俈嶜丅
丂丂丂俛揦偺傒偩偲丄侾侽侽侽墌亊係亖係侽侽侽墌丂偱丄係俉嶜庤偵擖傞丅
丂丂丂巆傝偺俋侽侽墌暘偱丄俠揦傛傝丄俋俀墌亊俋亖俉俀俉墌攦偄丄俋嶜庤偵擖傞丅埲忋偱丄俆俈嶜丅
丂丂丂俠揦偺傒偩偲丄俋俀墌亊俆俁亖係俉俈俇墌丂偱丄俆俁嶜偟偐攦偊側偄丅
丂丂埲忋偐傜丄係俋侽侽墌埲撪偱庤偵擖傟傞偙偲偑偱偒傞僲乕僩偼嵟戝俆俈嶜丅
乮俁乯丂峫偊傜傟傞慻偼丄慡晹偱侾侽捠傝丅
|
侾 |
俀 |
俁 |
係 |
俆 |
俇 |
俈 |
俉 |
俋 |
10 |
| 俙揦 |
俆侽 |
侽 |
侽 |
侽 |
侽 |
侽 |
侽 |
侽 |
侽 |
侽 |
| 俛揦 |
侽 |
係俉 |
係俋 |
俆侽 |
俆侾 |
俆俀 |
俆俁 |
俆係 |
俆俆 |
俆俇 |
| 俠揦 |
俈 |
俋 |
俉 |
俈 |
俇 |
俆 |
係 |
俁 |
俀 |
侾 |
乮捛婰乯丂暯惉俁侽擭俀寧俇擔乮壩乯晅偗挬擔怴暦挬姧偵暯惉俁侽擭搙奐惉拞妛擖帋栤戣偑宖
丂丂丂丂嵹偝傟偨丅柺敀偦偆側偺傪僠儑僀僗偟偰挧愴偟偰傒偨丅乮堦晹夵戣乯
侾乮俀乯愒媴丄惵媴丄墿媴偑俀屄偢偮俇屄偁傝傑偡丅摨偠怓偺媴偑椬傝崌傢側偄傛偆偵俇屄偡傋
丂丂丂偰傪嵍偐傜塃傊堦楍偵暲傋傑偡丅偙偺傛偆側暲傋曽偼壗捠傝偁傞偐媮傔側偝偄丅偨偩偟丄
丂丂丂摨偠怓偺媴偼嬫暿偟側偄偙偲偵偟傑偡丅
丂弴楍丒慻崌偣偺岞幃傪巊偍偆偲偡傞傕嵙愜丅慺捈偵庽宍恾偱峌傔傞偺偑椙偝偦偆偩丅
乮夝乯丂堦斣嵍偑愒媴偱偦偺椬偑惵媴偺偲偒丄
丂丂丂丂愒亅惵亅愒亅惵丂偼婲偙傝偊側偄丅
丂丂丂丂愒亅惵亅愒亅墿亅惵亅墿
丂丂丂丂愒亅惵亅墿亅愒亅惵亅墿
丂丂丂丂愒亅惵亅墿亅愒亅墿亅惵
丂丂丂丂愒亅惵亅墿亅惵亅愒亅墿
丂丂丂丂愒亅惵亅墿亅惵亅墿亅愒丂丂偺俆捠傝
丂堦斣嵍偲偦偺椬偺慻崌偣丂愒亅墿丄惵亅愒丄惵亅墿丄墿亅愒丄墿亅惵丂偱傕摨條丅
丂傛偭偰丄媮傔傞応崌偺悢偼丄丂俆亊俇亖俁侽乮捠傝乯
乮俁乯丂愳偺忋棳偺俙挰偲壓棳偺俛挰偺娫傪慏偱墲暅偟傑偡丅俙挰偐傜俛挰傑偱偼係俀暘偐偐傝丄
丂丂俛挰偐傜俙挰傑偱偼侾帪娫俆俀暘偐偐傝傑偡丅慏偺惷悈偱偺懍偝偼愳偺棳傟傞懍偝偺壗攞
丂丂偐摎偊側偝偄丅慏偺惷悈偱偺懍偝偲丄愳偺棳傟傞懍偝偼偦傟偧傟堦掕偲偟傑偡丅
乮夝乯丂俙挰偲俛挰偺娫偺嫍棧傪俴丄慏偺惷悈偱偺懍偝傪倁丄愳偺棳傟傞懍偝傪倂偲偡傞偲丄
丂丂丂俴/乮倁亄倂乯亖俈/侾侽丂丄俴/乮倁亅倂乯亖俀俉/侾俆丂側偺偱丄
丂丂丂乮俈/侾侽乯乮倁亄倂乯亖乮俀俉/侾俆乯乮倁亅倂乯
丂丂丂傛偭偰丄丂俁俆倁亖俈俈倂丂傛傝丄丂倁亖乮侾侾/俆乯倂
丂丂丂埲忋偐傜丄慏偺惷悈偱偺懍偝偼愳偺棳傟傞懍偝偺俀丏俀攞
乮僐儊儞僩乯丂暥帤傪巊偭偨夝朄偩偑丄嶼悢揑偵偼偳偆夝偔偺偩傠偆丠
乮係乯丂梕婍俙偵偼擹搙侾丏俇俀亾偺怘墫悈偑俇侽侽倗丄梕婍俛偵偼擹搙偺暘偐傜側偄怘墫悈偑
丂丂係侽侽倗擖偭偰偄傑偡丅俙偺怘墫悈偺偆偪俶倗傪俛偵堏偟偰傛偔偐偒崿偤偨偺偪丄摨偠俶倗傪俙
丂丂偵栠偟傑偟偨丅偝傜偵傑偨摨偠偙偲傪孞傝曉偟偨偲偙傠丄俙丄俛偺怘墫悈偺擹搙偼丄弴偵
丂丂侾丏俉俉亾偲俀丏侽係亾偵側傝傑偟偨丅嵟弶偺俛偺怘墫悈偺擹搙傪媮傔側偝偄丅
丂摉俫俹偺乽堄奜側幚尡乿偱偺峫嶡偑栶偵棫偪偦偆偩丅
乮夝乯丂梕婍俛偺怘墫悈偺擹搙傪 倶 亾偲偡傞丅俙仺俛偍傛傃俛仺俙偺憖嶌偺慜偲屻偱怘墫検
丂丂丂偼晄曄側偺偱丄
丂丂丂乮侽丏侽侾俇俀亊俇侽侽亄乮倶/侾侽侽乯亊係侽侽亖侽丏侽侾俉俉亊俇侽侽亄侽丏侽俀侽係亊係侽侽
丂丂丂丂俋丏俈俀亄係倶亖侾侾丏俀俉亄俉丏侾俇丂傛傝丄丂係倶亖俋丏俈俀丂偡側傢偪丄丂倶亖俀丏係俁乮亾乯
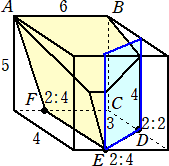
乮俆乯丂壓偺恾偼丄偁傞棫懱偺揥奐恾偱偡丅俛丄俠丄俢偼堦曈偑俇們倣偺惓曽宍丄俙丄俤丄俥偼捈
丂丂妏擇摍曈嶰妏宍丄俧偼惓嶰妏宍偱偡丅偙偺棫懱偺懱愊傪媮傔側偝偄丅
丂丂丂丂丂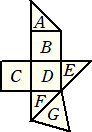
乮夝乯丂尦偺棫懱偼丄堦曈偑俇們倣偺棫曽懱偐傜妏偺嶰妏悕傪庢傝彍偄偨壓恾偺捠傝偱偁傞丅
丂丂丂丂丂
丂棫曽懱偺懱愊偼丄俇亊俇亊俇亖俀侾俇乮們倣3乯
丂嶰妏悕偺懱愊偼丄俇亊俇亊乮侾/俀乯亊俇亊乮侾/俁乯亖俁俇乮們倣3乯
丂傛偭偰丄媮傔傞棫懱偺懱愊偼丄丂俀侾俇亅俁俇亖侾俉侽乮們倣3乯
乮俇乯丂柺愊偑俋們倣2偱偁傞惓榋妏宍俙俛俠俢俤俥偺奺曈偺拞揰傪寢傫偱怴偟偄惓榋妏宍傪嶌
丂丂傝傑偡丅怴偟偄惓榋妏宍偺柺愊傪媮傔側偝偄丅壓偺恾偺揰俷偼懳徧偺拞怱偱偡丅
丂丂丂丂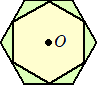
乮夝乯丂尦偺惓榋妏宍偲怴偟偄惓榋妏宍偺憡帡斾偼丄丂俀丗 丂側偺偱丄柺愊斾偼丄丂係丗俁
丂側偺偱丄柺愊斾偼丄丂係丗俁
丂丂丂傛偭偰丄怴偟偄惓榋妏宍偺柺愊偼丄丂俋亊乮俁/係乯亖俀俈/係乮們倣2乯
乮俈乯丂壓偺恾偵偍偄偰丄巐妏宍ABCD偼惓曽宍偱丄俛俤亖俤俥亖俥俠丄俠俧亖俧俢丂偱偡丅
乮鶣乯丂嶰妏宍俙俬俰偲巐妏宍ABCD偺柺愊斾傪嵟傕娙扨側惍悢偺斾偱摎偊側偝偄丅
乮鶤乯丂巐妏宍俫俬俰俲偲巐妏宍ABCD偺柺愊斾傪嵟傕娙扨側惍悢偺斾偱摎偊側偝偄丅
丂丂丂丂
乮夝乯
丂丂丂丂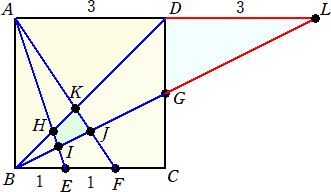
乮鶣乯丂忋恾偵偍偄偰丄巐妏宍ABCD偺柺愊亖俋丄仮俙俤俥偺柺愊亖俁/俀
丂丂丂AI 丗 俬俤亖俇丗侾丂側偺偱丄仮俙俬俥偺柺愊亖乮俁/俀乯乮俇/俈乯亖俋/俈
丂丂丂俙俰 丗 俰俥亖俁丗侾丂側偺偱丄仮俙俬俰偺柺愊亖乮俋/俈乯亊乮俁/係乯亖俀俈/俀俉
丂丂傛偭偰丄丂嶰妏宍俙俬俰偲巐妏宍ABCD偺柺愊斾偼丄丂俀俈/俀俉 丗 俋亖俁 丗 俀俉丂偲側傞丅
乮鶤乯丂忋恾偵偍偄偰丄巐妏宍ABCD偺柺愊亖俋丄仮俙俤俥偺柺愊亖俁/俀
丂丂丂俙俫 丗 俫俤亖俁丗侾丂側偺偱丄仮俙俫俥偺柺愊亖乮俁/俀乯乮俁/係乯亖俋/俉
丂丂丂俙俲 丗 俲俥亖俁丗俀丂側偺偱丄仮俙俫俲偺柺愊亖乮俋/俉乯乮俁/俆乯亖俀俈/係侽
丂丂傛偭偰丄丂巐妏宍俫俬俰俲偺柺愊亖仮俙俬俰亅仮俙俫俲亖俀俈/俀俉亅俀俈/係侽亖俉侾/俀俉侽丂傛傝丄
丂丂巐妏宍俫俬俰俲偲巐妏宍ABCD偺柺愊斾偼丄丂俉侾/俀俉侽 丗 俋亖俋 丗 俀俉侽
俀丏捈慄忋偵拞怱傪帩偮敿墌偑忋壓岎屳偵宷偑偭偨乽摴楬乿偑偁傝傑偡丅偙偺摴楬偺堦斣嵍
丂偺揰傪俙偲偟傑偡丅
丂丂丂丂
丂侾/俈傪彫悢偱昞偟丄偦偺彫悢戞侾埵偺悢帤傪侾斣栚偺敿墌偺敿宎丄彫悢戞俀埵偺悢帤傪
俀斣栚偺敿墌偺敿宎丄丒丒丒丂偲偟傑偡丅
丂俙偐傜偙偺摴楬傪摴偺傝俀侽侾俉倣恑傫偩抧揰偼丄嵍偐傜壗斣栚偺敿墌忋偺揰偲側傞偐丄摎
偊側偝偄丅
乮夝乯丂侾/俈亖侽丏侾係俀俉俆俈侾係俀俉俆俈丒丒丒丂偲弞娐偡傞彫悢偱偁傞丅
丂丂侾廃婜暘偺墌屖偺挿偝偼丄墌廃棪傪俁丏侾係偲偟偰丄
丂丂丂乮侾亄係亄俀亄俉亄俆亄俈乯亊俁丏侾係亖俀俈亊俁丏侾係亖俉係丏俈俉
丂丂傛偭偰丄丂俀侽侾俉亐俉係丏俈俉亖俀俁丏俉侽俀丒丒丒
丂丂丂俉係丏俈俉亊俀俁亖侾俋係俋丏俋係丂丂丂俀侽侾俉亅侾俋係俋丏俋係亖俇俉丏侽俇
丂丂偦偙偱丄丂侾亊俁丏侾係亖俁丏侾係丂丒丒丒丒丒丂俁丏侾係
丂丂丂丂丂丂丂係亊俁丏侾係亖侾俀丏俆俇丂丒丒丒丒丒丂侾俆丏俈
丂丂丂丂丂丂丂俀亊俁丏侾係亖俇丏俀俉丂丒丒丒丒丒丂俀侾丏俋俉
丂丂丂丂丂丂丂俉亊俁丏侾係亖俀俆丏侾俀丂丒丒丒丒丒丂係俈丏侾
丂丂丂丂丂丂丂俆亊俁丏侾係亖侾俆丏俈丂丒丒丒丒丒丂俇俀丏俉
丂丂丂丂丂丂丂俈亊俁丏侾係亖俀侾丏俋俉丂丒丒丒丒丒丂俉係丏俈俉
丂偟偨偑偭偰丄媮傔傞揰偼丄嵍偐傜丂俇亊乮俀俁亄侾乯亖侾係係斣栚偺敿墌忋偵偁傞丅
俁丏丂惓曽宍偺儅僗偺拞偵丄侾偼侾屄丄俀偼俀屄丄俁偼俁屄偺傛偆偵惍悢値偼値屄巊偄丄偁傞惍
丂丂悢偐傜楢懕偟偨俁庬椶埲忋偺惍悢傪恾偺傛偆偵彫偝偄弴偵暲傋傑偡丅
丂丂丂丂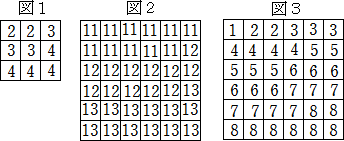
丂恾侾偱偼俁儅僗巐曽偺惓曽宍偵丄俀傪俀屄丄俁傪俁屄丄係傪係屄丄偪傚偆偳暲傋偒傝傑偟偨丅恾俀丄
恾俁偱偼丄俇儅僗巐曽偺惓曽宍偵侾侾偐傜侾俁傑偱丄侾偐傜俉傑偱偺惍悢傪偪傚偆偳暲傋偒傝傑偟
偨丅乮俇儅僗巐曽偵暲傋傞暲傋曽偼偙偺俀捠傝埲奜偁傝傑偣傫丅乯
丂恾侾偺夝傪丄亂俀乣係亃丄恾俀偺夝傪丄亂侾侾乣侾俁亃丄恾俁偺夝傪丄亂侾乣俉亃偲昞偡偙偲偵偟傑偡丅
丂師偺栤偄偵摎偊側偝偄丅乮侾乯丄乮俀乯偱偼丄俀捠傝埲忋偺暲傋曽偑偁傞応崌偼丄偡傋偰摎偊傞
偙偲丅
乮侾乯丂俈儅僗巐曽偺惓曽宍偵偪傚偆偳暲傋偒傞偵偼丄偄偔偮偐傜偄偔偮傑偱偺惍悢傪暲傋傟偽
丂丂傛偄偱偡偐丅
乮俀乯丂侾侽儅僗巐曽偺惓曽宍偵偪傚偆偳暲傋偒傞偵偼丄偄偔偮偐傜偄偔偮傑偱偺惍悢傪暲傋傟
丂丂偽傛偄偱偡偐丅
乮俁乯丂俁侽儅僗巐曽偺惓曽宍偵偪傚偆偳暲傋偒傞暲傋曽偼壗捠傝偁傝傑偡偐丅傑偨丄偦傟偧傟
丂丂偺暲傋曽偼壗庬椶偺惍悢傪巊偆偐媮傔側偝偄丅
丂丂乮俇儅僗巐曽偺惓曽宍偵偪傚偆偳暲傋偒傞暲傋曽偼恾俀丄恾俁偺亂侾侾乣侾俁亃丄亂侾乣俉亃偺俀
丂丂捠傝偱偡丅偙偺応崌偵偼俀捠傝偺暲傋曽偑偁傝丄偦傟偧傟乵俁丆俉乶庬椶偺惍悢傪巊偆乿偲摎
丂丂偊傞偙偲丅傑偨丄庬椶傪帵偡惍悢偼彫偝偄弴偵暲傋傞偙偲丅乯
乮夝乯乮侾乯丂俈2亖係俋丂偱丄丂値亄乮値亄侾乯亄丒丒丒亄倣亖係俋丂偲側傞 値丄倣 乮値亝倣乯傪尒偮偗傟偽傛偄丅
丂丂丂丂丂乮値亄倣乯丒倓亖俋俉亖俀丒俈2
丂丂丂倓亞俁丂偵拲堄偟偰丄
丂丂丂丂丂倓亖俈丂偺偲偒丄丂値亄倣亖値亄乮値亄俇乯亖俀値亄俇亖侾係丂傛傝丄丂値亖係丂丄倣亖侾侽
丂丂丂丂丂倓亖侾係丂偺偲偒丄丂値亄倣亖値亄乮値亄侾俁乯亖俀値亄侾俁亖俈丂偼夝側偟丅
丂丂丂丂丂倓亖係俋丂偺偲偒丄丂値亄倣亖値亄乮値亄係俉乯亖俀値亄係俉亖俀丂偼夝側偟丅
丂丂丂丂傛偭偰丄夝偼丄亂係乣侾侽亃
乮俀乯丂侾侽2亖侾侽侽丂偱丄丂値亄乮値亄侾乯亄丒丒丒亄倣亖侾侽侽丂偲側傞 値丄倣 乮値亝倣乯傪尒偮偗傟偽
丂丂傛偄丅
丂丂丂丂丂乮値亄倣乯丒倓亖俀侽侽亖俀3丒俆2
丂丂丂倓亞俁丂偵拲堄偟偰丄
丂丂丂丂丂倓亖係丂偺偲偒丄丂値亄倣亖値亄乮値亄俁乯亖俀値亄俁亖俆侽丂偼夝側偟
丂丂丂丂丂倓亖俆丂偺偲偒丄丂値亄倣亖値亄乮値亄係乯亖俀値亄係亖係侽丂傛傝丄丂値亖侾俉丂丄倣亖俀俀
丂丂丂丂丂倓亖俉丂偺偲偒丄丂値亄倣亖値亄乮値亄俈乯亖俀値亄俈亖俀俆丂傛傝丄丂値亖俋丂丄倣亖侾俇
丂丂丂丂丂倓亖侾侽丂偺偲偒丄丂値亄倣亖値亄乮値亄俋乯亖俀値亄俋亖俀侽丂偼夝側偟
丂丂丂丂丂倓亖俀侽丂偺偲偒丄丂値亄倣亖値亄乮値亄侾俋乯亖俀値亄侾俋亖侾侽丂偼夝側偟
丂丂丂丂丂倓亖俀俆丂偺偲偒丄丂値亄倣亖値亄乮値亄俀係乯亖俀値亄俀係亖俉丂偼夝側偟
丂丂丂丂丂倓亖係侽丂偺偲偒丄丂値亄倣亖値亄乮値亄俁俋乯亖俀値亄俁俋亖俆丂偼夝側偟
丂丂丂丂丂倓亖俆侽丂偺偲偒丄丂値亄倣亖値亄乮値亄係俋乯亖俀値亄係俋亖係丂偼夝側偟
丂丂丂丂丂倓亖侾侽侽丂偺偲偒丄丂値亄倣亖値亄乮値亄俋俋乯亖俀値亄俋俋亖俀丂偼夝側偟
丂丂丂丂丂倓亖俀侽侽丂偺偲偒丄丂値亄倣亖値亄乮値亄侾俋俋乯亖俀値亄侾俋俋亖侾丂偼夝側偟
丂丂丂丂傛偭偰丄夝偼丄亂侾俉乣俀俀亃丄亂俋乣侾俇亃
乮俁乯丂俁侽2亖俋侽侽丂偱丄丂値亄乮値亄侾乯亄丒丒丒亄倣亖俋侽侽丂偲側傞 値丄倣 乮値亝倣乯傪尒偮偗傟
丂丂偽傛偄丅
丂丂丂丂丂乮値亄倣乯丒倓亖侾俉侽侽亖俀3丒俁2丒俆2
丂丂倓亞俁丂偵拲堄偟偰丄
丂丂倓亖俁丄係丄俆丄俇丄俉丄俋丄侾侽丄侾俀丄侾俆丄侾俉丄俀侽丄俀係丄俀俆丄俁侽丄俁俇丄係侽丄係俆丄俆侽丄俇侽丄
丂丂丂丂俈俀丄俈俆丄俋侽丆侾侽侽丄侾俀侽侾俆侽丄侾俉侽丄俀侽侽丄俀俀俆丄俁侽侽丄俁俇侽丄係俆侽丄俇侽侽丄俋侽侽丄
丂丂丂丂侾俉侽侽
丂偙偺偆偪丄倓亖係丄俇丄侾侽丄侾俀丄侾俉丄俀侽丄俁侽丄俁俇丄係俆丄俆侽丄俇侽丄俈俀丄俈俆丄俋侽丆侾侽侽丄
丂丂丂丂丂丂丂丂丂侾俀侽侾俆侽丄侾俉侽丄俀侽侽丄俀俀俆丄俁侽侽丄俁俇侽丄係俆侽丄俇侽侽丄俋侽侽丄侾俉侽侽
丂丂偵偮偄偰偼丄夝偼側偄丅夝偑偁傞偺偼丄倓亖俁丄俆丄俉丄俋丄侾俆丄俀係丄俀俆丄係侽丂偺俉捠傝丅
丂傛偭偰丄乵俁丄俆丄俉丄俋丄侾俆丄俀係丄俀俆丄係侽乶庬椶偺惍悢傪巊偆丅
乮僐儊儞僩乯丂惍悢榑偺抦幆傪梡偄傟偽傕偭偲旤偟偔夝偗傞偲巚傢傟傞偑丄彫妛惗偵側偭偨婥暘
丂丂丂丂丂丂偱揇廘偔夝偄偰傒傑偟偨丅
乮捛婰乯丂拀攇戝妛晬懏嬵応拞妛乮暯惉俁侽擭搙擖帋乯偐傜柺敀偦偆側栤戣偵挧愴偟偰傒偨丅
[俁]丂嶰妏宍俙俛俠偺撪懁偵揰俹偑偁傝丄俹偐傜曈俛俠丄俠俙丄俙俛偵偦傟偧傟悅捈側慄傪堷偒丄
丂丂岎傢偭偨揰傪弴偵丄俢丄俤丄俥偲偟傑偡丅師偺栤偄偵摎偊側偝偄丅
乮俀乯丂壓偺恾偺傛偆偵丄嶰妏宍俙俛俠偼惓嶰妏宍偱偁傝丄俙俥偺挿偝偼俈們倣丄俛俢偺挿偝偼俉們倣丄
丂丂丂俠俤偺挿偝偼侾侽們倣偱偡丅偙偺偲偒丄惓嶰妏宍偺堦曈偺挿偝傪媮傔傛丅
丂丂丂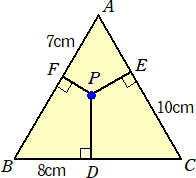
丂堦尒偡傞偲擄偟偦偆側偺偩偑丄乮侾乯偵乮俀乯偵宷偑傞曗彆慄偺僸儞僩傕梌偊傜傟偰偄傞偺偱丄師
偺傛偆偵峫偊傞偙偲偼丄傎傏堦杮摴偩傠偆丅
丂丂丂
乮夝乯丂仮俙俛俠偺奺曈偵暯峴偵揰俹傪捠傞捈慄傪堷偒丄仮俙俛俠撪偵彫惓嶰妏宍傪嶌傞丅
丂丂丂偙偺偲偒丄丂俉亅倷亖俀倶丂丄俈亅倶亖俀倸丂丄侾侽亅倸亖俀倷丂偑惉傝棫偮偺偱丄
丂丂俁幃傪曈乆壛偊偰丄丂俀俆亖俁乮倶亄倷亄倸乯丂傛傝丄丂倶亄倷亄倸亖俀俆/俁
丂丂偙偺偲偒丄惓嶰妏宍偺堦曈偺挿偝偼丄丂俀乮倶亄倷亄倸乯亖俆侽/俁
乮捛婰乯丂暯惉俁侾擭俀寧侾俀擔晅偗
丂暯惉俁侾擭俀寧俇擔乮悈乯晅偗挬擔怴暦挬姧偵暯惉俁侾擭搙嶗堻拞妛擖帋栤戣偑宖嵹偝傟
偨丅偄偔偮偐柺敀偦偆側栤戣偑偁偭偨偺偱丄彫妛惗偵側偭偨偮傕傝偱峫偊偰傒偨丅
嘥乮侾乯丂乮俁亄俆/俀係亄侽丏俀俀俆乯亐乮侾亄侾侾/侾俆乯亅侾丏俀俆亊侾侽/侾俁丂傪寁嶼偣傛丅
乮夝乯丂梌幃亖乮俁亄俆/俀係亄俋/係侽乯亐乮侾亄侾侾/侾俆乯亅乮俆/係乯亊侾侽/侾俁
丂丂丂丂丂丂亖乮俁亄俆俀/侾俀侽乯亐乮俀俇/侾俆乯亅乮俀俆/俀俇乯
丂丂丂丂丂丂亖乮侾侽俁/俁侽乯亐乮俀俇/侾俆乯亅乮俀俆/俀俇乯
丂丂丂丂丂丂亖乮侾侽俁/俆俀乯亅乮俀俆/俀俇乯
丂丂丂丂丂丂亖俆俁/俆俀乮亖侾亄侾/俆俀乯丂丂乮廔乯
乮僐儊儞僩乯丂偄傠偄傠寁嶼偺岺晇傪峫偊偰傒傑偟偨偑忋婰偺傛偆偵恀柺栚偵寁嶼偡傞偟偐側
丂丂丂丂丂丂偄偱偡偐偹丠
嘥乮俀乯暯惉俁侾擭俀寧侾擔偼嬥梛擔偱偡丅尦崋偑暯惉偵側偭偰偐傜丄偆傞偆擭偼乮丂乯夞
丂丂偁傝丄俁夞栚偺偆傞偆擭偺俀寧俀俋擔偼乮丂乯梛擔偱偟偨丅偨偩偟丄師偵偆傞偆擭偵側傞
丂丂偺偼俀侽俀侽擭偱丄暯惉偵側偭偰偐傜偆傞偆擭偼係擭偛偲偵偁傝傑偟偨丅
乮夝乯丂侾俋俉俋擭偐傜俀侽侾俉擭傑偱丄偆傞偆擭偼丄
丂丂丂侾俋俋俀擭丄侾俋俋俇擭丄俀侽侽侽擭丄俀侽侽係擭丄俀侽侽俉擭丄俀侽侾俀擭丄俀侽侾俇擭丂偺俈夞
丂丂俁夞栚偺偆傞偆擭偼俀侽侽侽擭偱丄俁寧侾擔乣侾俀寧俁侾擔偼丄俁侽俇擔娫
丂丂俀侽侽侾擭乣俀侽侾俉擭傑偱偺侾俉擭娫偼丄丂俁俇俆亊侾係亄俁俇俇亊係亖俇俆俈係擔娫
丂丂俀侽侾俋擭侾寧侾擔乣俀寧侾擔偼丄俁俀擔娫
丂丂丂埲忋偺崌寁偼丄丂俁侽俇亄俇俆俈係亄俁俀亖俇俋侾俀擔娫
丂丂偙偙偱丄丂俇俋侾俀亐俈亖俋俉俈丒丒丒俁丂側偺偱丄俀侽侽侽擭俁寧侾擔偼悈梛擔
丂丂傛偭偰丄俁夞栚偺偆傞偆擭偺俀寧俀俋擔偼丄壩梛擔偲側傞丅丂丂乮廔乯
乮僐儊儞僩乯丂忋婰偱偼擔悢寁嶼偱媮傔偨偑丄俁俇俆亐俈亖俆俀丒丒丒侾側偺偱丄暯惉俁侾擭俀寧侾擔
丂丂丂丂丂丂偑嬥梛擔側傜偽丄慜擭偺俀寧侾擔偼栘梛擔偲側傝丄侾偮暘孞傝忋偑傞丅摿偵丄偆傞
丂丂丂丂丂丂偆擭偼俀偮暘孞傝忋偑傞丅偙偺傛偆偵峫偊傞偲丄俀侽侽侽擭俀寧侾擔偼壩梛擔偲側傝丄
丂丂丂丂丂丂傛偭偰丄俀寧俀俋擔傕壩梛擔偲側傞丅
丂師偺栤戣偼戣堄偺棟夝偵屗榝偄夝摎曽恓偑棫偰偵偔偄丅擄栤偺晹椶偵擖傞偐側丠
嘩丂塃偺恾偺傛偆側偐傢偭偨帪寁偑偁傝傑偡丅偙偺帪寁
丂偵偼丄俈偐傜侾俈傑偱偺悢帤偲栚惙傝偑彂偄偰偁傝傑偡丅
丂俈偲俉丄俉偲俋丄俋偲侾侽丄丒丒丒丄侾俇偲侾俈偺栚惙傝偺娫妘偼丄
丂偡傋偰摍偟偄偲偟傑偡丅屵慜俈帪傪俈帪侽暘丄屵屻侾帪傪
丂侾俁帪侽暘偺傛偆偵昞偡偙偲偵偟傑偡丅俉帪侽暘偺偲偒丄塃
丂偺恾偺傛偆偵帪寁偺挿恓偼俈丄抁恓偼俉傪巜偟傑偡丅挿
丂恓偲抁恓偼塃夞傝偵側傔傜偐偵摦偒傑偡丅 |
丂丂 |
丂挿恓偼師偺嘆嘇偺婯懃偵廬偭偰摦偒傑偡丅
嘆丂挿恓偼俈帪侽暘偐傜侾俈帪侽暘傑偱偼俇侽暘偱侾廃偟傑偡丅偙偺偲偒丄挿恓偲抁恓偼
丂丂偦傟偧傟堦掕偺懍偝偱摦偒傑偡丅
嘇丂挿恓偼侾俈帪侽暘偐傜梻擔偺俈帪侽暘傑偱偼侾俇俉暘偱侾廃偟傑偡丅偙偺偲偒丄挿恓
丂丂偲抁恓偼偦傟偧傟堦掕偺懍偝偱摦偒傑偡丅
丂挿恓偑侾廃偡傞娫偵抁恓偑夞揮偡傞妏搙偼丄嘆偺偲偒傕嘇偺偲偒傕摨偠偱丄抁恓偼
俀係帪娫偱侾廃偟傑偡丅偨偩偟丄晛捠偺帪寁偲摨偠傛偆偵侾帪娫偼俇侽暘偱偡丅
乮侾乯丂師偺乮丂丂乯偵偁偰偼傑傞悢傪摎偊側偝偄丅
丂挿恓偑侾廃偡傞娫偵抁恓偑夞揮偡傞妏搙偼乮丂丂乯亱偱偡丅
丂帪崗偑侾俀帪係俆暘偺偲偒偺挿恓偲抁恓偺偮偔傞妏偺戝偒偝偼乮丂丂乯亱偱偡丅
丂偨偩偟丄挿恓偲抁恓偺偮偔傞妏偺戝偒偝偼侽亱埲忋侾俉侽亱埲壓偲偟傑偡丅
乮俀乯丂侾侽帪侽暘偐傜侾侾帪侽暘傑偱偺侾帪娫偱丄挿恓偲抁恓偺偮偔傞妏偺戝偒偝偑俇侽亱
丂丂偵側傞帪崗偼壗帪壗暘偱偡偐丅偡傋偰媮傔側偝偄丅
乮俁乯丂侾俈帪侽暘偐傜梻擔偺俈帪侽暘偺娫偱丄挿恓偲抁恓偑廳側傞帪崗偼壗帪壗暘偱偡
丂丂偐丅偡傋偰媮傔側偝偄丅
乮夝乯乮侾乯丂挿恓偼侾俈帪侽暘偐傜梻擔偺俈帪侽暘傑偱偼侾俇俉暘偱侾廃偡傞偺偱丄
丂丂丂丂丂丂俇侽亊侾係亐侾俇俉亖俆丂偡側傢偪丄挿恓偼俆廃偡傞偙偲偵側傞丅
丂丂丂丂丂挿恓偼丄俈帪侽暘偐傜侾俈帪侽暘傑偱偼丄侾侽廃偡傞偺偱丄崌傢偣偰侾擔偱丄侾俆廃
丂丂丂丂偟偨偑偭偰丄抁恓偼丄挿恓偑侾廃偡傞娫偵丂俁俇侽亱亐侾俆亖俀係亱夞揮偡傞丅
丂丂丂帪崗偑侾俀帪係俆暘偺偲偒丄挿恓偺埵抲偼丄乽俈乿偐傜塃夞傝偵應偭偰丄俀俈侽亱
丂丂丂抁恓偺埵抲偼丄乽俈乿偐傜塃夞傝偵應偭偰丄丂俀係亱亊乮俆亄俁/係乯亖侾俁俉亱
丂丂丂傛偭偰丄挿恓偲抁恓偺偮偔傞妏偺戝偒偝偼丄丂俀俈侽亱亅侾俁俉亱亖侾俁俀亱
乮俀乯丂媮傔傞帪崗傪侾侽帪倣暘偲偡傞偲丄
丂丂挿恓偺埵抲偼丄乽俈乿偐傜塃夞傝偵應偭偰丄俁俇侽亱亊乮倣/俇侽乯亖俇亱亊倣
丂丂抁恓偺埵抲偼丄乽俈乿偐傜塃夞傝偵應偭偰丄俀係亱亊乮俁亄倣/俇侽乯亖俈俀亱亄乮俀/俆乯亱亊倣
丂傛偭偰丄戣堄傛傝丄丂丂俈俀亱亄乮俀/俆乯亱亊倣亇俇侽亱亖俇亱亊倣
丂偡側傢偪丄丂乮俀俉/俆乯亱亊倣亖侾俀亱傑偨偼丂侾俁俀亱傛傝丄丂倣亖侾俆/俈丂丄侾俇俆/俈
丂丂埲忋偐傜丄媮傔傞帪崗偼丄丂侾侽帪乮俀亄侾/俈乯暘丂丄侾侽帪乮俀俁亄係/俈乯暘
乮僐儊儞僩乯丂忋婰偱偼暥帤倣傪梡偄偰偟傑偭偨偑丄暥帤傪梡偄側偄夝朄傕傕偪傠傫懚嵼偡傞丅
丂丂丂丂丂丂憡懳懍搙偺峫偊曽傪梡偄傞丅
乮暿夝乯丂侾侽帪傑偱偵抁恓偼丄俀係亱亊俁亖俈俀亱恑傫偱偄傞丅
丂丂丂丂丂抁恓偼丄俇侽暘偱俀係亱恑傓偺偱丄枅暘侽丏係亱恑傓丅
丂丂丂丂丂挿恓偼丄俇侽暘偱俁俇侽亱恑傓偺偱丄枅暘俇亱恑傓丅
丂丂丂傛偭偰丄抁恓傪屌掕偟偨偲偒偺挿恓偺恑傓懍偝偼丄丂俇亱亅侽丏係亱亖俆丏俇亱
丂丂丂戣堄傛傝丄挿恓偲抁恓偺偮偔傞妏偺戝偒偝偑俇侽亱側偺偱丄
丂丂丂丂乮俈俀亱亅俇侽亱乯亐俆丏俇亱亖侾俆/俈乮暘乯
丂丂丂丂乮俈俀亱亄俇侽亱乯亐俆丏俇亱亖侾俇俆/俈乮暘乯
丂丂埲忋偐傜丄媮傔傞帪崗偼丄丂侾侽帪乮俀亄侾/俈乯暘丂丄侾侽帪乮俀俁亄係/俈乯暘
乮俁乯丂偙傟傕憡懳懍搙偺峫偊曽偱媮傔偨曽偑偄偄栤戣偩傠偆丅
丂侾俈帪侽暘偐傜梻擔偺俈帪侽暘偺娫偱丄
丂丂挿恓偼丄侾俇俉暘偱俁俇侽亱側偺偱丄枅暘俁俇侽亱/侾俇俉亖乮侾俆/俈乯亱
丂丂抁恓偼丄侾俇俉暘偱俀係亱側偺偱丄枅暘俀係亱/侾俇俉亖乮侾/俈乯亱
丂側偺偱丄抁恓傪屌掕偟偨偲偒偺挿恓偺憡懳懍搙偼丄丂乮侾俆/俈乯亱亅乮侾/俈乯亱亖俀亱
丂抁恓偺埵抲偑乽侾俈乿偵偁傞偲偒丄乽俈乿偺埵抲偐傜塃夞傝偵應偭偰丄俀係亱亊侾侽亖俀係侽亱
丂偙偺俀係侽亱偺埵抲偵挿恓偑撏偔偵偼丄丂俀係侽亱亐俀亱亖侾俀侽乮暘乯丂偐偐傞丅
丂傛偭偰丄丂侾俈亄俀亖侾俋丂傛傝丄丂侾俋帪侽暘偵挿恓偲抁恓偑廳側傞丅
丂偙偺乽侾俋乿偺埵抲偐傜挿恓偑侾廃偟偰傑偨挿恓偲抁恓偑廳側傞偺偼丄
丂俁俇侽亱亐俀亱亖侾俉侽乮暘乯丂偐偐傞丅埲壓丄摨條偵偟偰丄挿恓偲抁恓偑廳側傞偺偼丄
丂俀俀帪侽暘丂丄侾帪侽暘丂丄係帪侽暘丂丄俈帪侽暘
丂埲忋偐傜丄媮傔傞帪崗偼丄
丂侾俋帪侽暘丂丄俀俀帪侽暘丂丄侾帪侽暘丂丄係帪侽暘丂丄俈帪侽暘丂丂乮廔乯
乮捛婰乯丂暯惉俁侾擭俁寧係擔晅偗
嘨丂嬻偺戝偒側悈偦偆 倎丄倐丄們 偲丄梕婍俙丄俛丄俠偑侾偮偢偮偁傝傑偡丅梕婍俙丄俛丄俠偵
丂丂擖傟傞偙偲偑偱偒傞怘墫悈偺廳偝偼丄崌傢偣偰俇侽侽倗偱偡丅俁偮偺梕婍偵偦傟偧傟
丂丂怘墫悈傪偄偭傁偄偵側傞傑偱擖傟偰偐傜丄俁偮偺梕婍偵擖傟偨怘墫悈傪偡傋偰侾偮
丂丂偺悈偦偆偵堏偡丄偲偄偆嶌嬈傪偟傑偡丅
丂丂丂梕婍俙丄俛丄俠偺偡傋偰偵擹搙偑侾侽亾偺怘墫悈傪偄偭傁偄偵側傞傑偱擖傟偨偁偲丄
丂丂悈偦偆倎偵堏偟傑偟偨丅
乮侾乯梕婍俙丄俛丄俠偵偦傟偧傟擹搙偑侾俆亾丄侾侽亾丄侾侽亾偺怘墫悈傪偄偭傁偄偵側傞
丂丂傑偱擖傟偨偁偲丄悈偦偆倐偵堏偟丄偝傜偵悈偦偆倐偵悈傪侾侽侽倗擖傟傞偲丄悈偦偆倎偲
丂丂悈偦偆倐偺擹搙偼摨偠偵側傝傑偟偨丅梕婍俙偵偼壗倗偺怘墫悈偑擖傝傑偡偐丅
乮俀乯梕婍俙丄俛丄俠偵偦傟偧傟擹搙偑侾俀亾丄俈亾丄侾俁亾偺怘墫悈傪偄偭傁偄偵側傞傑
丂丂偱擖傟偨偁偲丄悈偦偆們偵堏偟偨偲偙傠丄悈偦偆倎偲斾傋偰悈偦偆們偵娷傑傟傞怘墫偺
丂丂検偼俆丏俉倗懡偔側傝傑偟偨丅梕婍俛偵偼壗倗偺怘墫悈偑擖傝傑偡偐丅
乮夝乯丂梕婍俙丄俛丄俠偵擖傞怘墫悈偺廳偝傪俙丄俛丄俠偱昞偡偲偒丄丂俙亄俛亄俠亖俇侽侽
乮侾乯丂侽丏侾俆俙亄侽丏侾俛亄侽丏侾俠亖侽丏侾亊俈侽侽亖俈侽
丂丂丂侽丏侾俙亄侽丏侾俛亄侽丏侾俠亖俇侽丂側偺偱丄丂侽丏侽俆俙亖侾侽丂傛偭偰丄丂俙亖俀侽侽倗
乮俀乯丂侽丏侾俀亊俀侽侽亄侽丏侽俈俛亄侽丏侾俁乮係侽侽亅俛乯亖俇俆丏俉丂傛傝丄丂俛亖侾俈侽倗丂丂乮廔乯
乮僐儊儞僩乯丂曽掱幃傪梡偄偰夝偄偰偄傑偡偑丄嶼悢揑側夝朄傕懚嵼偡傞偱偟傚偆丅嶗堻偺庴尡
丂丂丂丂丂丂惗偵偲偭偰偼丄愨懳姰摎偡傋偒暯堈側栤戣偱偟偨丅
乮捛婰乯丂暯惉俁侾擭俁寧俈擔晅偗
嘦丂乮侾乯敿宎俇們倣丄拞怱妏侾俋搙偺愵宍A偺巻偲丆敿宎俁們倣丄拞怱妏侾俋搙偺愵宍B
丂丂丂丂偺巻偑偨偔偝傫偁傝傑偡丅
丂丂丂丂丂丂丂丂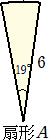 丂丂丂丂丂丂
丂丂丂丂丂丂
乮僀乯 A偺巻偩偗傪壓恾偺傛偆偵偼傝崌傢偣偰墌傪嶌傝傑偡丅偺傝偟傠晹暘偺柺愊偺崌
丂寁偑偄偪偽傫彫偝偔側傞傛偆偵偼傝崌傢偣偨偲偒丄偺傝偟傠晹暘偺柺愊偺崌寁偼
丂壗們倣2偱偡偐丅
丂丂丂丂丂丂丂
乮儘乯 A丄B偺巻傪壓恾偺傛偆偵A偲B偑昁偢岎屳偵側傞傛偆偵丄暯傜偵偼傝崌傢偣傑偡丅
丂偺傝偟傠晹暘偺柺愊偺崌寁偑偄偪偽傫彫偝偔側傞傛偆偵偼傝崌傢偣偨偲偒丄偱偒偨恾
丂宍偺廃偺挿偝偼壗們倣偱偡偐丅
丂丂丂丂丂丂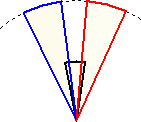
丂乮僀乯乮儘乯偵偍偄偰丆嵟屻偵偼傞巻偼1枃栚偺巻偵偼傝崌傢偣丄偺傝偟傠晹暘偺愵宍
偺拞怱妏偼偳傟傕俁搙埲忋偵側傝傑偡丅傑偨丄巻偑俁枃忋廳側傞晹暘偼偁傝傑偣傫丅
乮夝乯乮侾乯丂偺傝偟傠晹暘偺愵宍偺拞怱妏傪兤偲偍偒丄偺傝偟傠晹暘偺屄悢傪 値 屄偲偡傞偲丄
丂丂戣堄傛傝丄丂乮侾俋亱亅兤乯亊値亖俁俇侽亱
丂丂偙偙偱丄兤亞俁亱側偺偱丄侾俋亱亅兤亝侾俇亱傛傝丄値亞俁俇侽/侾俇亖俀俀丏俆
丂丂値偼帺慠悢側偺偱丄嵟彫抣偼丄俀俁屄
丂偙偺偲偒丄丂乮侾俋亱亅兤乯亊俀俁亖俁俇侽亱傛傝丄丂兤亖侾俋亱亅俁俇侽亱/俀俁亖俈俈亱/俀俁
丂傛偭偰丄偺傝偟傠晹暘偺柺愊偺崌寁偼丄
丂丂俁俇兾亊乮俈俈亱/俀俁乯亊俀俁亐俁俇侽亱亖俀係丏侾俈俉乮們倣2乯
乮俀乯丂偺傝偟傠晹暘偺愵宍偺拞怱妏傪兤偲偍偒丄偺傝偟傠晹暘偺屄悢傪 値 屄偲偡傞偲丄
丂丂乮侾乯偲摨條偵偟偰丄丂値亞俁俇侽/侾俇亖俀俀丏俆
丂丂戣堄傛傝丄A偲B偑昁偢岎屳偵側傞偺偱丄値偼嬼悢丅傛偭偰丄値偺嵟彫抣偼丄俀係屄
丂偙偺偲偒丄丂乮侾俋亱亅兤乯亊俀係亖俁俇侽亱傛傝丄丂兤亖侾俋亱亅俁俇侽亱/俀係亖係亱
丂傛偭偰丄媮傔傞恾宍偺廃偺挿偝偼丄
丂丂侾俀兾亊侾俋亱亊侾俀亐俁俇侽亱亄俇兾亊侾侾亱亊侾俀亐俁俇侽亱亄俇亊侾俀
丂亖係俋兾/俆亄俈俀亖侾侽俀丏俈俈俀乮們倣乯
乮捛婰乯丂暯惉俁侾擭俀寧俀俀擔晅偗
丂暯惉俁侾擭俀寧俆擔乮壩乯晅偗挬擔怴暦挬姧偵暯惉俁侾擭搙奐惉拞妛擖帋栤戣偑宖嵹偝傟
偨丅偄偔偮偐柺敀偦偆側栤戣偑偁偭偨偺偱丄彫妛惗偵側偭偨偮傕傝偱峫偊偰傒偨丅
俁丏丂嬻娫撪傑偨偼暯柺忋偵堷偐傟偨摴傪慖傫偱丄揰俙偐傜揰俛傑偱堏摦偡傞偲偒丄偦
丂丂偺堏摦宱楬偑壗捠傝嵼傞偐傪峫偊傞丅揰俙偲揰俛傪寢傇懢慄偑捠傞偙偲偑弌棃傞
丂丂摴偱偁傞丅偙傟傜偺摴傪丄塃丄忋傑偨偼墱偺壗傟偐偺曽岦偵恑傓偙偲偱丄揰俙偐傜
丂丂揰俛傑偱堏摦偡傞偲偒丄峫偊傜傟傞堏摦宱楬偼丄佱恾侾佲丄佱恾俀佲偺偦傟偧傟偵
丂丂偮偄偰壗捠傝偁傝傑偡偐丅
乮侾乯丂師偺佱恾侾佲偼丄堦曈偺挿偝偑侾偺棫曽懱傪係屄慻傒崌傢偣偨傕偺偱偁傞丅
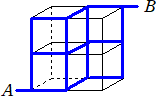 |
丂丂乮夝乯丂暯柺偱峫偊偰丄丂5俠2亖侾侽乮捠傝乯丂丂乮廔乯 |
丂師偺佱恾俀佲偼堦曈偺挿偝偑侾偺棫曽懱傪係屄慻傒崌傢偣偨傕偺偱偁傞丅
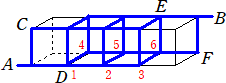 |
丂丂乮夝乯丂俙仺俠仺俛丂偼丄丂侾亊3俠1亖俁乮捠傝乯
丂丂丂丂丂丂俙仺俢仺俤仺俛丂偱丄1,2,3,4,5,6偺偳偙偱忋偵
丂丂丂丂忋偑傞偐偱応崌暘偗偡傟偽丄
丂丂1仺3捠傝丄2仺2捠傝丄3仺1捠傝丄4仺1捠傝丄5仺2捠傝丄
丂丂6仺3捠傝
丂丂丂俙仺俢仺俥仺俛丂偼丄侾亊3俠1亊侾亖俁乮捠傝乯
丂傛偭偰丄丂俁亄侾俀亄俁亖侾俉乮捠傝乯丂丂乮廔乯 |
乮俀乯丂 師偺傛偆側婯懃偵廬偭偰偙傟傜偺摴傪捠傝丄揰俙偐傜揰俛傑偱堏摦偡傞偙偲傪峫
丂丂丂偊傞丅
丂丂婯懃丗堦夞偩偗嵍偵侾恑傒丄偦傟埲奜偼塃傑偨偼忋偵恑傓
丂偨偩偟丄恑傓曽岦傪曄峏偱偒傞偺偼惓曽宍偺捀揰偺応強偩偗偱偁傞丅揰俙偵栠偭偨
傝丄揰俛偐傜栠偭偨傝偼弌棃側偄丅傑偨丄婯懃偵廬偆尷傝丄摨偠摴傪俀夞埲忋捠傞偙偲傕
壜擻偱偁傞丅
丂師偺佱恾俁佲丄佱恾係佲丄佱恾俆佲偺偦傟偧傟偵偮偄偰丄峫偊傜傟傞堏摦宱楬偼壗
捠傝偁傞偐丅
丂師偺佱恾俁佲偼堦曈偺挿偝偑侾偺惓曽宍傪俀屄暲傋偨傕偺偱偁傞丅
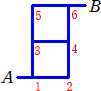 |
丂丂乮夝乯丂2,4,6偺偳偙偐偱嵍偵恑傓偺偱丄
丂丂丂丂丂2仺3捠傝丄4仺4捠傝丄6仺3捠傝
丂丂丂丂傛偭偰丄丂俁亄係亄俁亖侾侽乮捠傝乯丂丂乮廔乯 |
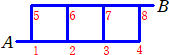
丂師偺佱恾係佲偼堦曈偺挿偝偑侾偺惓曽宍傪俁屄暲傋偨傕偺偱偁傞丅
 |
丂丂乮夝乯丂2,3,4,6,7,8偺偳偙偐偱嵍偵恑傓偺偱丄
丂丂丂丂丂2仺4捠傝丄3仺3捠傝丄4仺2捠傝丄
丂丂丂丂丂6仺2捠傝丄7仺3捠傝丄8仺4捠傝
丂丂丂丂傛偭偰丄丂俀乮係亄俁亄俀乯亖侾俉乮捠傝乯丂丂乮廔乯丂 |
丂師偺佱恾俆佲偼堦曈偺挿偝偑侾偺惓曽宍傪俇屄暲傋偨傕偺偱偁傞丅
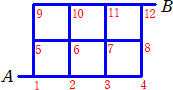 |
丂丂乮夝乯丂2,3,4,6,7,8,10,11,12偺偳偙偐偱嵍偵恑傓偺偱丄
丂丂丂丂丂2仺10捠傝丄3仺6捠傝丄4仺3捠傝丄
丂丂丂丂丂6仺8捠傝丄7仺9捠傝丄8仺8捠傝
丂丂丂丂丂10仺3捠傝丄11仺6捠傝丄12仺10捠傝
丂丂丂丂傛偭偰丄丂俀乮侾侽亄俇亄俁亄俉乯亄俋亖俇俁乮捠傝乯丂丂乮廔乯丂丂 |
乮僐儊儞僩乯丂忋婰偺寁嶼偱偼丄慻崌偣乮n俠r乯傪梡偄偰偄傞偑丄庤寁嶼偱傕廫暘懳墳壜擻偱
丂丂丂丂丂丂偟傚偆丅
乮捛婰乯丂暯惉俁侾擭俁寧俁擔晅偗
侾丏丂俲孨偼丄帺戭偐傜偍偽偝傫偺壠傑偱丄僗僀僇俀偮傪堦恖偱塣傇偮傕傝偱偟偨丅偲偙傠
丂丂偑丄掜偺俽孨偑乽傏偔傕庤揱偆!乿偲尵偭偨偺偱丄師偺傛偆偵偟傑偟偨丅
丂侾乯俲孨偲俽孨偑偦傟偧傟僗僀僇傪1偮偢偮帩偭偰丄摨帪偵帺戭傪弌敪偡傞丅
丂俀乯俲孨偺曽偑俽孨傛傝恑傓懍偝偑懍偄偺偱丄偍偽偝傫偺壠偵愭偵拝偔丅偦偙偱丄偡偖
丂丂偵僗僀僇傪抲偄偰丄俽孨偵弌夛偆傑偱堷偒曉偡丅
丂俁乯俲孨偼丄俽孨偵弌夛偭偨傜偡偖偵俽孨偐傜僗僀僇傪庴偗庢傝丄偡偖偵偍偽偝傫偺壠
丂丂偵岦偐偆丅
偙偙偱丄俲孨偺恑傓懍偝偼
丂僗僀僇傪俀偮帩偭偰偄傞偲偒偼 枅暘 俇侽倣
丂僗僀僇傪侾偮帩偭偰偄傞偲偒偼 枅暘 俉侽倣
丂僗僀僇傪帩偭偰偄側偄偲偒偼 枅暘 侾侽侽倣
偱偡丅
僗僀僇俀偮傪塣傃廔偊偨俲孨偑偍偽偝傫偺壠偱媥傫偱偄傞偲丄屻偐傜捛偄偐偗偰偒偨俽
孨偑摓拝偟傑偟偨丅
俽孨 乽偍偵偄偪傖傫丄傏偔丄栶偵棫偭偨?乿
俲孨 乽傕偪傠傫偩傛! 傏偔偑堦恖偱塣傇偮傕傝偩偭偨偗偳丄偦偆偡傞偺偵斾傋偰丄15/16
丂丂丂攞偺帪娫偱塣傃廔偊傜傟偨偐傜偹丅偁傝偑偲偆!乿
俽孨 乽傎傫偲!? 傛偐偭偨!乿
師偺栤偵摎偊側偝偄丅
乮侾乯俲孨偑堦搙栚偵偍偽偝傫偺壠偵拝偄偰偐傜丄擇搙栚偵偍偽偝傫偺壠偵拝偔傑偱偺
丂丂帪娫偼丄俲孨偑偼偠傔偵堦恖偱僗僀僇俀偮傪塣傇偺偵偐偐傞偲峫偊偰偄偨帪娫偺壗
丂丂攞偱偡偐丅
乮俀乯堷偒曉偟偨俲孨偑俽孨偵弌夛偭偨抧揰偐傜丄偍偽偝傫偺壠傑偱偺嫍棧偼丄帺戭偐
丂丂傜偍偽偝傫偺壠傑偱偺嫍棧偺壗攞偱偡偐丅
乮俁乯俽孨偑僗僀僇傪侾偮帩偭偰恑傓懍偝偼枅暘壗倣偱偡偐丅
乮夝乯丂帺戭偐傜偍偽偝傫偺壠傑偱偺嫍棧傪 倶 倣丄俲孨偑俽孨偵弌夛偭偰偐傜偍偽偝傫偺壠
丂丂傑偱偺嫍棧傪 倷 倣丄摉弶偺梊掕帪娫傪俿暘偲偡傞偲丄戣堄傛傝丄
丂丂丂丂倶/俉侽亄倷/侾侽侽亄倷/俉侽亖乮侾俆/侾俇乯俿丂丄丂倶/俇侽亖俿
偑惉傝棫偮丅
乮侾乯丂媮傔傞帪娫偼丄倷/侾侽侽亄倷/俉侽丂側偺偱丄
丂丂丂倷/侾侽侽亄倷/俉侽亖乮侾俆/侾俇乯俿亅倶/俉侽亖乮侾俆/侾俇乯俿亅乮俇侽/俉侽乯俿亖乮俁/侾俇乯俿
丂丂傛偭偰丄摉弶偺梊掕帪娫偺丂俁/侾俇丂攞偱偁傞丅
乮俀乯丂倷/侾侽侽亄倷/俉侽亖乮俁/侾俇乯俿亖乮俁/侾俇乯乮倶/俇侽乯亖乮侾/俁俀侽乯倶丂傛傝丄
丂丂丂乮俋/係侽侽乯倷亖乮侾/俁俀侽乯倶丂側偺偱丄丂倷亖乮俆/俁俇乯倶
丂丂傛偭偰丄媮傔傞嫍棧偼丄帺戭偐傜偍偽偝傫偺壠傑偱偺嫍棧偺丂俆/俁俇丂攞偱偁傞丅
乮俁乯丂俽孨偺恑傓懍偝傪枅暘 倸 倣偲偡傞偲丄戣堄傛傝丄
丂丂丂丂丂倶/俉侽亄倷/侾侽侽亖乮俁侾/俁俇乯倶/倸
丂倷亖乮俆/俁俇乯倶丂傪戙擖偟偰惍棟偡傞偲丄丂倸乮侾/俉侽亄侾/俈俀侽乯亖俁侾/俁俇
丂丂傛偭偰丄丂倷亖乮俁侾/俁俇乯亊俈俀亖俇俀丂傛傝丄俽孨偺恑傓懍偝偼枅暘 俇俀 倣丂丂乮廔乯
乮僐儊儞僩乯丂戝恖偘側偔曽掱幃傪棫偰偰夝偄偰偟傑偄傑偟偨偑丄嶼悢揑側傕偭偲僄儗僈儞僩側夝
丂丂丂丂丂丂朄偑偁傞偺偱偟傚偆偹丏丏丏懡暘両
乮捛婰乯丂椷榓俀擭俀寧7擔晅偗
丂椷榓俀擭俀寧俆擔乮悈乯晅偗挬擔怴暦挬姧偵椷榓俀擭搙奐惉拞妛擖帋栤戣偑宖嵹偝傟偨丅
偄偔偮偐柺敀偦偆側栤戣偑偁偭偨偺偱丄彫妛惗偵側偭偨偮傕傝偱峫偊偰傒偨丅
俁丏丂僋儔僗慡堳偐傜寛傑偭偨嬥妟傪廤傔偲偒丄廤傔傗偡偔偡傞偨傔偵師偺儖乕儖傪嶌
丂丂偭偨丅
丂儖乕儖侾丗巊偊傞偍嬥偼丄侾墌丄俆墌丄侾侽墌丄俆侽墌丄侾侽侽墌丄俆侽侽墌偺俇庬椶偺峝
丂丂丂丂丂丂壿偲偡傞丅
丂儖乕儖俀丗偍偮傝偑側偄傛偆偵梡堄偡傞丅
丂儖乕儖俁丗峝壿偼丄侾恖偵偮偒侾侽枃傑偱偲偡傞丅
乮侾乯丂僋儔僗係侽恖偐傜俀俉墌偢偮廤傔傞偙偲偵偟偨丅
丂乮傾乯儖乕儖偵崌偆傛偆偵俀俉墌傪帩偭偰偔傞曽朄偼慡晹偱壗捠傝偁傞偐丅
丂乮僀乯廤傑偭偨偍嬥偺偆偪丄侾墌嬍偑侾俇俆枃偁偭偨丅偙偺偲偒丄俆墌嬍傪侾枃傕帩偭偰偙
丂丂丂側偐偭偨惗搆偼壗恖偐丅
乮夝乯乮侾乯乮傾乯丂壓昞偵傛傝丄係捠傝
|
侾墌 |
俆墌 |
10墌 |
| 侾 |
俁 |
侾 |
俀 |
| 俀 |
俉 |
侽 |
俀 |
| 俁 |
俁 |
俁 |
侾 |
| 係 |
俁 |
俆 |
侽 |
乮僀乯丂係侽恖慡堳偑俆墌嬍傪侾枃埲忋偼帩偭偰偒偨偲偡傞偲丄侾墌嬍偺屄悢偼丄侾俀侽枃偵側傞丅
丂丂偲偙傠偑丄侾墌嬍偺屄悢偼丄侾俇俆枃側偺偱丄丂侾俇俆亅侾俀侽亖係俆乮枃乯
丂丂傛偭偰丄侾墌嬍偺屄悢偺嵎偼丄俉亅俁亖俆乮枃乯側偺偱丄丂係俆亐俆亖俋乮恖乯
丂丂偟偨偑偭偰丄俆墌嬍傪侾枃傕帩偭偰偙側偐偭偨惗搆偼丄俋恖丅
乮俀乯丂偙偺儖乕儖偵偮偄偰丄俀恖偺夛榖偺嬻強傪曗廩偣傛丅
丂俙丗峝壿偑懡偔側傝夁偓側偄傛偆偵偟偨偗偳丄偙偺儖乕儖偩偲廤傔傜傟側偄嬥妟偑偁傞
丂丂偹丅
丂俛丗妋偐偵丄椺偊偽俁俉俋墌偩偲丄嵟掅偱傕乮丂嘆丂乯枃偺峝壿偑昁梫偱丄儖乕儖俁偑庣
丂丂傟側偄偹丅
丂俙丗偙偺傛偆側嬥妟偭偰丄偳傟偔傜偄偁傞偺偐側丅
丂俛丗堦斣掅偄嬥妟偼乮丂嘇丂乯墌偩偲暘偐傞偗偳丄偨偔偝傫偁傝偦偆丅
丂俙丗係俋墌傑偱偺嬥妟傪梡堄偡傞偺偵昁梫側嵟掅枃悢偺昞傪嶌偭偰傒偨傛丅
| 嵟掅枃悢乮枃乯 |
嬥妟乮墌乯 |
壗捠傝偐乮捠傝乯 |
| 侾 |
侾丄俆丄10 |
俁 |
| 俀 |
俀丄俇丄11丄15丄20 |
俆 |
| 俁 |
俁丄俈丄12丄16丄21丄25丄30 |
俈 |
| 係 |
係丄俉丄13丄17丄22丄26丄31丄35丄40 |
俋 |
| 俆 |
乮丂嘊丂乯 |
乮丂嘑丂乯 |
| 俇 |
乮丂嘋丂乯 |
乮丂嘒丂乯 |
| 俈 |
乮丂嘍丂乯 |
乮丂嘓丂乯 |
| 俉 |
乮丂嘐丂乯 |
乮丂嘔丂乯 |
| 俋 |
49 |
侾 |
丂俛丗偙偺忣曬偲俆侽墌嬍丄侾侽侽墌嬍丄俆侽侽墌嬍偺慻傒崌傢偣傪峫偊傞偲丄儖乕儖侾偲
丂丂俀傪庣傟偽丄儖乕儖俁傪庣傟側偄傕偺偼丄俁侽侽墌傑偱偺嬥妟偱偼丄乮丂嘕丂乯捠傝偁
丂丂傝丄侾侽侽侽墌傑偱偺嬥妟偱偼丄乮丂嘖丂乯捠傝偁傞偹丅
乮夝乯丂俁俉俋亖俁亊侾侽侽亄侾亊俆侽亄俁亊侾侽亄侾亊俆亄係亊侾丂傛傝丄
丂丂丂丂俁亄侾亄俁亄侾亄係亖侾俀乮枃乯丒丒丒嘆
丂丂堦斣掅偄嬥妟偼丄丂侾亊侾侽侽亄侾亊俆侽亄係亊侾侽亄侾亊俆亄係亊侾亖侾俋俋乮墌乯丒丒丒嘇
丂俋亖侾亊俆亄係亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俆枃
丂侾係亖侾亊侾侽亄係亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俆枃
丂侾俉亖侾亊侾侽亄侾亊俆亄俁亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俆枃
丂侾俋亖侾亊侾侽亄侾亊俆亄係亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俇枃
丂俀俁亖俀亊侾侽亄俁亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俆枃
丂俀係亖俀亊侾侽亄係亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俇枃
丂俀俈亖俀亊侾侽亄侾亊俆亄俀亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俆枃
丂俀俉亖俀亊侾侽亄侾亊俆亄俁亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俇枃
丂俀俋亖俀亊侾侽亄侾亊俆亄係亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俈枃
丂俁俀亖俁亊侾侽亄俀亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俆枃
丂俁俁亖俁亊侾侽亄俁亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俇枃
丂俁係亖俁亊侾侽亄係亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俈枃
丂俁俇亖俁亊侾侽亄侾亊俆亄侾亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俆枃
丂俁俈亖俁亊侾侽亄侾亊俆亄俀亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俇枃
丂俁俉亖俁亊侾侽亄侾亊俆亄俁亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俈枃
丂俁俋亖俁亊侾侽亄侾亊俆亄係亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俉枃
丂係侾亖係亊侾侽亄侾亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俆枃
丂係俀亖係亊侾侽亄俀亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俇枃
丂係俁亖係亊侾侽亄俁亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俈枃
丂係係亖係亊侾侽亄係亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俉枃
丂係俆亖係亊侾侽亄侾亊俆丂丒丒丒丂昁梫嵟掅枃悢丂俆枃
丂係俇亖係亊侾侽亄侾亊俆亄侾亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俇枃
丂係俈亖係亊侾侽亄侾亊俆亄俀亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俈枃
丂係俉亖係亊侾侽亄侾亊俆亄俁亊侾丂丒丒丒丂昁梫嵟掅枃悢丂俉枃
丂埲忋偐傜丄嘊仺丂俋丄侾係丄侾俉丄俀俁丄俀俈丄俁俀丄俁俇丄係侾丄係俆丂丂嘑仺丂俋
丂丂丂丂丂丂丂嘋仺丂侾俋丄俀係丄俀俉丄俁俁丄俁俈丄係俀丄係俇丂丂嘒仺丂俈
丂丂丂丂丂丂丂嘍仺丂俀俋丄俁係丄俁俉丄係俁丄係俈丂丂嘓仺丂俆
丂丂丂丂丂丂丂嘐仺丂俁俋丄係係丄係俉丂丂嘔仺丂俁
丂儖乕儖俁傪庣傟側偄傕偺
丂侾乣係俋偱昁梫嵟掅枃悢俋乮係俋乯偺偲偒丄俁侽侽墌埲撪偺傕偺偼丄
丂丂俀枃捛壛丒丒丒丂侾亊俆侽亄侾亊侾侽侽乮仺丂侾俋俋乯丄俀亊侾侽侽乮仺丂俀係俋乯
丂丂俁枃捛壛丒丒丒丂侾亊俆侽亄俀亊侾侽侽乮仺丂俀俋俋乯
丂丂嬥妟偼丄丂侾俋俋丄俀係俋丄俀俋俋
丂侾乣係俋偱昁梫嵟掅枃悢俉乮俁俋丄係係丄係俉乯偺偲偒丄俁侽侽墌埲撪偺傕偺偼丄
丂丂俁枃捛壛丒丒丒丂侾亊俆侽亄俀亊侾侽侽乮仺丂俀俉俋丄俀俋係丄俀俋俉乯
丂丂嬥妟偼丄丂俀俉俋丄俀俋係丄俀俋俉
丂埲忋偐傜丄儖乕儖俁傪庣傟側偄傕偺偱俁侽侽墌埲撪偺嬥妟偼丄
丂丂侾俋俋丄俀係俋丄俀俋俋丄俀俉俋丄俀俋係丄俀俋俉
偺俇捠傝丒丒丒嘕
丂摨條偵偟偰丄
丂儖乕儖俁傪庣傟側偄傕偺
丂侾乣係俋偱昁梫嵟掅枃悢俋乮係俋乯偺偲偒丄侾侽侽侽墌埲撪偺傕偺偼丄
丂丂俀枃捛壛丒丒丒丂侾亊俆侽亄侾亊侾侽侽乮仺丂侾俋俋乯丄俀亊侾侽侽乮仺丂俀係俋乯
丂丂丂丂丂丂丂丂丂丂侾亊俆侽亄侾亊俆侽侽乮仺丂俆俋俋乯丄侾亊侾侽侽亄侾亊俆侽侽乮仺丂俇係俋乯
丂丂俁枃捛壛丒丒丒丂侾亊俆侽亄俀亊侾侽侽乮仺丂俀俋俋乯丄俁亊侾侽侽乮仺丂俁係俋乯丄
丂丂丂丂丂丂丂丂丂丂侾亊俆侽亄侾亊侾侽侽亄侾亊俆侽侽乮仺丂俇俋俋乯丄俀亊侾侽侽亄侾亊俆侽侽乮仺丂俈係俋乯
丂丂係枃捛壛丒丒丒丂侾亊俆侽亄俁亊侾侽侽乮仺丂俁俋俋乯丄係亊侾侽侽乮仺丂係係俋乯丄
丂丂丂丂丂丂丂丂丂丂侾亊俆侽亄俀亊侾侽侽亄侾亊俆侽侽乮仺丂俈俋俋乯丄俁亊侾侽侽亄侾亊俆侽侽乮仺丂俉係俋乯
丂丂俆枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽乮仺丂係俋俋乯丄侾亊俆侽亄俁亊侾侽侽亄侾亊俆侽侽乮仺丂俉俋俋乯丄
丂丂丂丂丂丂丂丂丂丂係亊侾侽侽亄侾亊俆侽侽乮仺丂俋係俋乯
丂丂俇枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽亄侾亊俆侽侽乮仺丂俋俋俋乯
丂丂嬥妟偼丄丂侾俋俋丄俀係俋丄俆俋俋丄俇係俋丄俀俋俋丄俁係俋丄俇俋俋丄俈係俋丄俁俋俋丄係係俋丄俈俋俋丄
丂丂丂丂丂丂丂丂係俋俋丄俉係俋丄俉俋俋丄俋係俋丄俋俋俋丂丂侾俇屄
丂侾乣係俋偱昁梫嵟掅枃悢俉乮俁俋丄係係丄係俉乯偺偲偒丄侾侽侽侽墌埲撪偺傕偺偼丄
丂丂俁枃捛壛丒丒丒丂侾亊俆侽亄俀亊侾侽侽乮仺丂俀俉俋丄俀俋係丄俀俋俉乯丄
丂丂丂丂丂丂丂丂丂丂俁亊侾侽侽乮仺丂俁俁俋丄俁係係丄俁係俉乯丄俀亊侾侽侽亄侾亊俆侽侽乮仺丂俈俁俋丄俈係係丄俈係俉乯丄
丂丂丂丂丂丂丂丂丂丂侾亊俆侽亄侾亊侾侽侽亄侾亊俆侽侽乮仺丂俇俉俋丄俇俋係丄俇俋俉乯
丂丂係枃捛壛丒丒丒丂侾亊俆侽亄俁亊侾侽侽乮仺丂俁俉俋丄俁俋係丄俁俋俉乯丄
丂丂丂丂丂丂丂丂丂丂係亊侾侽侽乮仺丂係俁俋丄係係係丄係係俉乯丄俁亊侾侽侽亄侾亊俆侽侽乮仺丂俉俁俋丄俉係係丄俉係俉乯丄
丂丂丂丂丂丂丂丂丂丂侾亊俆侽亄俀亊侾侽侽亄侾亊俆侽侽乮仺丂俈俉俋丄俈俋係丄俈俋俉乯
丂丂俆枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽乮仺丂係俉俋丄係俋係丄係俋俉乯丄
丂丂丂丂丂丂丂丂丂丂係亊侾侽侽亄侾亊俆侽侽乮仺丂俋俁俋丄俋係係丄俋係俉乯丄
丂丂丂丂丂丂丂丂丂丂侾亊俆侽亄俁亊侾侽侽亄侾亊俆侽侽乮仺丂俉俉俋丄俉俋係丄俉俋俉乯
丂丂俇枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽亄侾亊俆侽侽乮仺丂俋俉俋丄俋俋係丄俋俋俉乯
丂丂嬥妟偼丄丂俀俉俋丄俀俋係丄俀俋俉丄俁俁俋丄俁係係丄俁係俉丄俈俁俋丄俈係係丄俈係俉丄俇俉俋丄俇俋係丄俇俋俉丄
丂丂丂丂丂丂丂丂俁俉俋丄俁俋係丄俁俋俉丄係俁俋丄係係係丄係係俉丄俉俁俋丄俉係係丄俉係俉丄俈俉俋丄俈俋係丄俈俋俉丄
丂丂丂丂丂丂丂丂係俉俋丄係俋係丄係俋俉丄俋俁俋丄俋係係丄俋係俉丄俉俉俋丄俉俋係丄俉俋俉丄俋俉俋丄俋俋係丄俋俋俉
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俁俇屄
丂侾乣係俋偱昁梫嵟掅枃悢俈乮俀俋丄俁係丄俁俉丄係俁丄係俈乯偺偲偒丄侾侽侽侽墌埲撪偺傕偺偼丄
丂丂係枃捛壛丒丒丒丂侾亊俆侽亄俁亊侾侽侽乮仺丂俁俈俋丄俁俉係丄俁俉俉丄俁俋俁丄俁俋俈乯丄
丂丂丂丂丂丂丂丂丂丂係亊侾侽侽乮仺丂係俀俋丄係俁係丄係俁俉丄係係俁丄係係俈乯丄
丂丂丂丂丂丂丂丂丂丂俁亊侾侽侽亄侾亊俆侽侽乮仺丂俉俀俋丄俉俁係丄俉俁俉丄俉係俁丄俉係俈乯丄
丂丂丂丂丂丂丂丂丂丂侾亊俆侽亄俀亊侾侽侽亄侾亊俆侽侽乮仺丂俈俈俋丄俈俉係丄俈俉俉丄俈俋俁丄俈俋俈乯
丂丂丂丂丂丂丂丂丂丂
丂丂俆枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽乮仺丂係俈俋丄係俉係丄係俉俉丄係俋俁丄係俋俈乯丄
丂丂丂丂丂丂丂丂丂丂侾亊俆侽亄俁亊侾侽侽亄侾亊俆侽侽乮仺丂俉俈俋丄俉俉係丄俉俉俉丄俉俋俁丄俉俋俈乯丄
丂丂丂丂丂丂丂丂丂丂係亊侾侽侽亄侾亊俆侽侽乮仺丂俋俀俋丄俋俁係丄俋俁俉丄俋係俁丄俋係俈乯
丂丂俇枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽亄侾亊俆侽侽乮仺丂俋俈俋丄俋俉係丄俋俉俉丄俋俋俁丄俋俋俈乯
丂丂嬥妟偼丄丂俁俈俋丄俁俉係丄俁俉俉丄俁俋俁丄俁俋俈丄係俀俋丄係俁係丄係俁俉丄係係俁丄係係俈丄俉俀俋丄俉俁係丄
丂丂丂丂丂丂丂丂俉俁俉丄俉係俁丄俉係俈丄俈俈俋丄俈俉係丄俈俉俉丄俈俋俁丄俈俋俈丄係俈俋丄係俉係丄係俉俉丄係俋俁丄
丂丂丂丂丂丂丂丂係俋俈丄俉俈俋丄俉俉係丄俉俉俉丄俉俋俁丄俉俋俈丄俋俀俋丄俋俁係丄俋俁俉丄俋係俁丄俋係俈丄俋俈俋丄
丂丂丂丂丂丂丂丂俋俉係丄俋俉俉丄俋俋俁丄俋俋俈丂係侽屄
丂侾乣係俋偱昁梫嵟掅枃悢俇乮侾俋丄俀係丄俀俉丄俁俁丄俁俈丄係俀丄係俇乯偺偲偒丄侾侽侽侽墌埲撪偺傕偺偼丄
丂丂俆枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽乮仺丂係俇俋丄係俈係丄係俈俉丄係俉俁丄係俉俈丄係俋俀丄係俋俇乯丄
丂丂丂丂丂丂丂丂丂丂侾亊俆侽亄俁亊侾侽侽亄侾亊俆侽侽乮仺丂俉俇俋丄俉俈係丄俉俈俉丄俉俉俁丄俉俉俈丄俉俋俀丄俉俋俇乯丄
丂丂丂丂丂丂丂丂丂丂係亊侾侽侽亄侾亊俆侽侽乮仺丂俋侾俋丄俋俀係丄俋俀俉丄俋俁俁丄俋俁俈丄俋係俀丄俋係俇乯
丂丂俇枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽亄侾亊俆侽侽乮仺丂俋俇俋丄俋俈係丄俋俈俉丄俋俉俁丄俋俉俈丄俋俋俀丄俋俋俇乯
丂丂嬥妟偼丄丂係俇俋丄係俈係丄係俈俉丄係俉俁丄係俉俈丄係俋俀丄係俋俇丄俉俇俋丄俉俈係丄俉俈俉丄俉俉俁丄
丂丂丂丂丂丂丂丂俉俉俈丄俉俋俀丄俉俋俇丄俋侾俋丄俋俀係丄俋俀俉丄俋俁俁丄俋俁俈丄俋係俀丄俋係俇丄俋俇俋丄俋俈係丄
丂丂丂丂丂丂丂丂俋俈俉丄俋俉俁丄俋俉俈丄俋俋俀丄俋俋俇丂丂俀俉屄
丂侾乣係俋偱昁梫嵟掅枃悢俆乮俋丄侾係丄侾俉丄俀俁丄俀俈丄俁俀丄俁俇丄係侾丄係俆乯偺偲偒丄侾侽侽侽墌埲
撪偺傕偺偼丄
丂丂俇枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽亄侾亊俆侽侽
丂丂丂丂丂丂丂丂丂丂乮仺丂俋俆俋丄俋俇係丄俋俇俉丄俋俈俁丄俋俈俈丄俋俉俀丄俋俉俇丄俋俋侾丄俋俋俆乯
丂丂嬥妟偼丄丂俋俆俋丄俋俇係丄俋俇俉丄俋俈俁丄俋俈俈丄俋俉俀丄俋俉俇丄俋俋侾丄俋俋俆丂丂俋屄
丂埲忋偐傜丄丂侾俇亄俁俇亄係侽亄俀俉亄俋亖侾俀俋屄丒丒丒嘖
乮僐儊儞僩乯丂抧摴偵悢偊偰傒偨偑丄偲偰傕戝曄偩偭偨丅偒偭偲傕偭偲僄儗僈儞僩側媮傔曽偑偁傞
丂丂丂丂丂丂偺偱偟傚偆丅
丂DD++偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俀擭俀寧俈擔晅偗乯
丂0墌偐傜4墌傑偱偱嵟掅枃悢偑偦偺枃悢偵側傞嬥妟僷僞乕儞偼丄0枃偐傜弴偵1,1,1,1,1
丂0墌偐傜9墌傑偱偱嵟掅枃悢偑偦偺枃悢偵側傞嬥妟僷僞乕儞偼丄n枃偺応崌丄5墌嬍偑偁偭偰
懠庬偱n-1枃偐丄5墌嬍偑側偔偰懠庬偱n枃偐偱峫偊傟偽傛偔丄偮傑傝丄椬傝崌偆2悢傪懌偣偽偄
偄乮抂偼屄悢偑尭傝傑偡偑乯偺偱丄0枃偐傜弴偵1,2,2,2,2,1
丂0墌偐傜49墌傑偱偱嵟掅枃悢偑偦偺枃悢偵側傞嬥妟僷僞乕儞偼丄摨條偵10墌嬍偑0枃偐傜
4枃偱応崌暘偗偡傞偺偱丄椬傝崌偆5悢傪懌偟偰峴偭偰丄0枃偐傜弴偵1,3,5,7,9,9,7,5,3,1
乮偙傟偑偡偱偵昞偵側偭偰偄傞偺偱丄幚嵺偼偙偙偐傜僗僞乕僩偱偒傞乯
丂摨條偵孞傝曉偡偲丄
丂0墌偐傜99墌傑偱偱嵟掅枃悢偑偦偺枃悢偵側傞嬥妟僷僞乕儞偼丄
0枃偐傜弴偵1,4,8,12,16,18,16,12,8,4,1
丂0墌偐傜499墌傑偱偱嵟掅枃悢偑偦偺枃悢偵側傞嬥妟僷僞乕儞偼丄
0枃偐傜弴偵1,5,13,25,41,58,70,74,70,58,41,25,13,5,1
丂0墌偐傜999墌傑偱偱嵟掅枃悢偑偦偺枃悢偵側傞嬥妟僷僞乕儞偼丄
0枃偐傜弴偵1,6,18,38,66,99,128,144,144,128,99,66,38,18,6,1
丂偙偙偐傜0墌乮0枃乯傪彍偄偰1000墌乮2枃乯傪壛偊傞偲丄1墌偐傜1000墌傑偱偱嵟掅枃悢偑偦
偺枃悢偵側傞嬥妟僷僞乕儞偼丄1枃偐傜弴偵
丂丂6,19,38,66,99,128,144,144,128,99,66,38,18,6,1
偲偄偆偙偲偱丄峝壿10枃埲撪偱巟暐偊側偄嬥妟偼丄66+38+18+6+1=129捠傝
仈忋婰偺乮夝乯偺傗傝曽傛傝偼偪傚偭偲憗偄乧乧偄傗丄偦偆偱傕側偄偐乧乧丠
乮僐儊儞僩乯丂忋婰偺乮夝乯偱偺寁嶼偱丄嬥庬傪彂偐側偗傟偽傕偭偲尒傗偡偔側傞偐側丠
乮俀乯丂偙偺儖乕儖偵偮偄偰丄俀恖偺夛榖偺嬻強傪曗廩偣傛丅
丂俙丗峝壿偑懡偔側傝夁偓側偄傛偆偵偟偨偗偳丄偙偺儖乕儖偩偲廤傔傜傟側偄嬥妟偑偁傞
丂丂偹丅
丂俛丗妋偐偵丄椺偊偽俁俉俋墌偩偲丄嵟掅偱傕乮丂嘆丂乯枃偺峝壿偑昁梫偱丄儖乕儖俁偑庣
丂丂傟側偄偹丅
丂俙丗偙偺傛偆側嬥妟偭偰丄偳傟偔傜偄偁傞偺偐側丅
丂俛丗堦斣掅偄嬥妟偼乮丂嘇丂乯墌偩偲暘偐傞偗偳丄偨偔偝傫偁傝偦偆丅
丂俙丗係俋墌傑偱偺嬥妟傪梡堄偡傞偺偵昁梫側嵟掅枃悢偺昞傪嶌偭偰傒偨傛丅
| 嵟掅枃悢乮枃乯 |
嬥妟乮墌乯 |
壗捠傝偐乮捠傝乯 |
| 侾 |
侾丄俆丄10 |
俁 |
| 俀 |
俀丄俇丄11丄15丄20 |
俆 |
| 俁 |
俁丄俈丄12丄16丄21丄25丄30 |
俈 |
| 係 |
係丄俉丄13丄17丄22丄26丄31丄35丄40 |
俋 |
| 俆 |
9丄14丄18丄23丄27丄32丄36丄41丄45 |
俋 |
| 俇 |
19丄24丄28丄33丄37丄42丄46 |
俈 |
| 俈 |
29丄34丄38丄43丄47 |
俆 |
| 俉 |
39丄44丄48 |
俁 |
| 俋 |
49 |
侾 |
丂俛丗偙偺忣曬偲俆侽墌嬍丄侾侽侽墌嬍丄俆侽侽墌嬍偺慻傒崌傢偣傪峫偊傞偲丄儖乕儖侾偲
丂丂俀傪庣傟偽丄儖乕儖俁傪庣傟側偄傕偺偼丄俁侽侽墌傑偱偺嬥妟偱偼丄乮丂嘕丂乯捠傝偁
丂丂傝丄侾侽侽侽墌傑偱偺嬥妟偱偼丄乮丂嘖丂乯捠傝偁傞偹丅
丂儖乕儖俁傪庣傟側偄傕偺
丂侾乣係俋偱昁梫嵟掅枃悢俋偺偲偒丄俁侽侽墌埲撪偺傕偺偼丄
丂丂俀枃捛壛丒丒丒丂侾亊俆侽亄侾亊侾侽侽丄俀亊侾侽侽
丂丂俁枃捛壛丒丒丒丂侾亊俆侽亄俀亊侾侽侽丂偱丄俁亊侾亖俁捠傝
丂侾乣係俋偱昁梫嵟掅枃悢俉偺偲偒丄俁侽侽墌埲撪偺傕偺偼丄
丂丂俁枃捛壛丒丒丒丂侾亊俆侽亄俀亊侾侽侽丂偱丄侾亊俁亖俁捠傝
丂埲忋偐傜丄儖乕儖俁傪庣傟側偄傕偺偱俁侽侽墌埲撪偺嬥妟偼丄俁亄俁亖俇捠傝丒丒丒嘕
丂摨條偵偟偰丄
丂儖乕儖俁傪庣傟側偄傕偺
丂侾乣係俋偱昁梫嵟掅枃悢俋偺偲偒丄侾侽侽侽墌埲撪偺傕偺偼丄
丂丂俀枃捛壛丒丒丒丂侾亊俆侽亄侾亊侾侽侽丄俀亊侾侽侽丄侾亊俆侽亄侾亊俆侽侽丄侾亊侾侽侽亄侾亊俆侽侽
丂丂俁枃捛壛丒丒丒丂侾亊俆侽亄俀亊侾侽侽丄俁亊侾侽侽丄侾亊俆侽亄侾亊侾侽侽亄侾亊俆侽侽丄俀亊侾侽侽亄侾亊俆侽侽
丂丂係枃捛壛丒丒丒丂侾亊俆侽亄俁亊侾侽侽丄係亊侾侽侽丄侾亊俆侽亄俀亊侾侽侽亄侾亊俆侽侽丄俁亊侾侽侽亄侾亊俆侽侽
丂丂俆枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽丄侾亊俆侽亄俁亊侾侽侽亄侾亊俆侽侽丄係亊侾侽侽亄侾亊俆侽侽
丂丂俇枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽亄侾亊俆侽侽丂偱丄丂侾俇亊侾亖侾俇捠傝
丂侾乣係俋偱昁梫嵟掅枃悢俉偺偲偒丄侾侽侽侽墌埲撪偺傕偺偼丄
丂丂俁枃捛壛丒丒丒丂侾亊俆侽亄俀亊侾侽侽丄俁亊侾侽侽丄俀亊侾侽侽亄侾亊俆侽侽丄侾亊俆侽亄侾亊侾侽侽亄侾亊俆侽侽
丂丂係枃捛壛丒丒丒丂侾亊俆侽亄俁亊侾侽侽丄係亊侾侽侽丄俁亊侾侽侽亄侾亊俆侽侽丄侾亊俆侽亄俀亊侾侽侽亄侾亊俆侽侽
丂丂俆枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽丄係亊侾侽侽亄侾亊俆侽侽丄侾亊俆侽亄俁亊侾侽侽亄侾亊俆侽侽
丂丂俇枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽亄侾亊俆侽侽丂偱丄丂侾俀亊俁亖俁俇捠傝
丂侾乣係俋偱昁梫嵟掅枃悢俈偺偲偒丄侾侽侽侽墌埲撪偺傕偺偼丄
丂丂係枃捛壛丒丒丒丂侾亊俆侽亄俁亊侾侽侽丄係亊侾侽侽丄俁亊侾侽侽亄侾亊俆侽侽丄侾亊俆侽亄俀亊侾侽侽亄侾亊俆侽侽
丂丂俆枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽丄侾亊俆侽亄俁亊侾侽侽亄侾亊俆侽侽丄係亊侾侽侽亄侾亊俆侽侽
丂丂俇枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽亄侾亊俆侽侽丂丂偱丄丂俉亊俆亖係侽捠傝
丂侾乣係俋偱昁梫嵟掅枃悢俇偺偲偒丄侾侽侽侽墌埲撪偺傕偺偼丄
丂丂俆枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽丄侾亊俆侽亄俁亊侾侽侽亄侾亊俆侽侽丄係亊侾侽侽亄侾亊俆侽侽
丂丂俇枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽亄侾亊俆侽侽丂丂偱丄丂係亊俈亖俀俉捠傝
丂侾乣係俋偱昁梫嵟掅枃悢俆偺偲偒丄侾侽侽侽墌埲撪偺傕偺偼丄
丂丂俇枃捛壛丒丒丒丂侾亊俆侽亄係亊侾侽侽亄侾亊俆侽侽丂丂偱丄侾亊俋亖俋捠傝
丂埲忋偐傜丄丂侾俇亄俁俇亄係侽亄俀俉亄俋亖侾俀俋屄丒丒丒嘖
仈彮偟偼尒傗偡偔側偭偨偐側丠偦傟偵偟偰傕峫偊偝偣傞栤戣偑嶐擭搙傛傝傕戝暆偵憹偊偨傛
丂偆側丏丏丏暤埻婥丅
丂傝傜傂偄偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俀擭俀寧俈擔晅偗乯
丂巹側傜偙偆悢偊傞偐側丅
丂1000墌偼嵟掅枃悢2枃偱偁傞丅1000墌枹枮偱壓擇偗偨偑00傑偨偼50偲側傞傕偺偺嵟掅枃
悢偼丄
丂50,100,500乧1枃
丂150,200,550,600乧2枃
丂250,300,650,700乧3枃
丂350,400,750,800乧4枃
丂450,850,900乧5枃
丂950乧6枃
丂傛偭偰丄偙傟傜偼10枃埲撪偱梡堄偱偒傞丅偙傟傜偺拞娫偺嬥妟偺嵟掅枃悢偼丄偦傟傛傝彫
偝偔偰堦斣嬤偄50偺攞悢偺嵟掅枃悢偲偦偺50偺攞悢傪堷偄偨1乣49偺嵟掅枃悢傪懌偟偨傕
偺偵側傞偺偱丄
丂10傪挻偊傞偺偼丄
丂2枃+9枃埲忋乧4*1=4捠傝
丂3枃+8枃埲忋乧4*(3+1)=16捠傝
丂4枃+7枃埲忋乧4*(5+3+1)=36捠傝
丂5枃+6枃埲忋乧3*(7+5+3+1)=48捠傝
丂6枃+5枃埲忋乧1*(9+7+5+3+1)=25捠傝
丂1000墌傑偱偱儖乕儖3傪庣傟側偄傕偺偼丄4+16+36+48+25=129捠傝
仈丂忋婰偺乮夝乯偲戝嵎偼側偔偰寢嬊戝曄側傫偱偡偗偳丅
丂偪側傒偵丄300墌傑偱偺偲偒偼丄
丂2枃+9枃埲忋乧2*1=2捠傝
丂3枃+8枃埲忋乧1*(3+1)=4捠傝
丂傛偭偰丄丂2+4=6捠傝
乮僐儊儞僩乯丂僗僢僉儕悢偊傜傟偰偄偰姶摦偟傑偟偨丅傝傜傂偄偝傫丄DD++偝傫偵姶幱偟傑偡丅
乮捛婰乯丂椷榓俀擭俀寧侾侽擔晅偗
丂俀侽俀侽擭侾寧侾俉擔乮搚乯偵峴傢傟偨撳拞妛峑偺擖帋栤戣乮侾擔栚乯偺師偺栤戣偵挧愴偟偰
傒傑偟偨丅
俁丏丂捈慄摴楬忋偵係抧揰俙丄俛丄俠丄俢偑弴偵暲傇丅俛俠娫偼俉係倣丄俠俢娫偼侾俀俇侽倣
丂丂棧傟偰偄傞丅嵟弶丄倃偔傫偼俙偵丄倄偔傫偼俠偵偄傞丅俀恖偑俛偵岦偐偭偰摨帪偵曕偒
丂丂巒傔傞偲丄摨帪偵俛偵摓拝偟偨丅傑偨丄嵟弶偺忬懺偐傜俀恖偑俢偵岦偐偭偰曕偒巒
丂丂傔傞偲丄摨帪偵俢偵摓拝偟偨丅偙偺偲偒丄俙俛娫偼壗倣棧傟偰偄傞偐丅偨偩偟丄倃偺曕
丂丂偔懍偝偼俛偵岦偐偆偲偒傕俢偵岦偐偆偲偒傕摨偠偲偟丄倄傕摨條偲偡傞丅
乮夝乯丂俙俛娫偺嫍棧傪倎偲偟丄倃偔傫丄倄偔傫偺懍偝傪偦傟偧傟倳丄倴偲偡傞偲丄
丂戣堄傛傝丄俉係/倴亖倎/倳丂丄乮倎亄侾俁係係乯/倳亖侾俀俇侽/倴
丂戞俀幃傛傝丄丂倎/倳亄侾俁係係/倳亖乮俉係/倴乯亊侾俆丂偡側傢偪丄丂倎/倳亄侾俁係係/倳亖乮倎/倳乯亊侾俆
丂傛偭偰丄丂侾俁係係/倳亖乮倎/倳乯亊侾係丂傛傝丄丂倎亖侾俁係係/侾係亖俋俇乮倣乯丂丂乮廔乯
乮僐儊儞僩乯丂曽掱幃傪棫偰傟偽忋婰偺傛偆偵夝偗傞偑丄堄枴傪峫偊傟偽師偺傛偆偵夝偔偺偑
丂丂丂丂丂丂嶼悢揑偱偟傚偆丅
丂倃偔傫偑俙偐傜俛偵偄偔帪娫偺侾俆攞偱丄倄偔傫偼俠偐傜俢偵偄偔丅
丂倃偔傫偑俙偐傜俛偵拝偄偨偲偒丄倄偔傫偼倃偔傫偑俙偐傜俛偵偄偔帪娫偩偗恑傫偱偄傞偺偱丄巆
傝帪娫偼丄倃偔傫偑俙偐傜俛偵偄偔帪娫偺侾係攞丅
丂偙偺帪娫偱倃偔傫偼丄侾俁係係倣傪恑傓偙偲偵側傞偺偱丄俙俛娫偺嫍棧偼丄
丂丂侾俁係係亐侾係亖俋俇乮倣乯偲尵偊傞丅
乮捛婰乯丂椷榓俀擭俀寧侾侾擔晅偗
丂椷榓俀擭俀寧係擔乮壩乯晅偗挬擔怴暦挬姧偵椷榓俀擭搙嶗堻拞妛擖帋栤戣偑宖嵹偝傟偨丅
偄偔偮偐柺敀偦偆側栤戣偑偁偭偨偺偱丄彫妛惗偵側偭偨偮傕傝偱峫偊偰傒偨丅
俬丏乮俀乯丂俙偲俛偼丄偍揦偱偍壻巕傪侾俀屄偢偮峸擖偟偨丅俙偼偦偺偆偪偺偄偔偮偐傪帩偪
丂婣傝丄巆傝偼偍揦偱怘傋偨丅俛偼俙偑偍揦偱怘傋偨屄悢偲摨偠屄悢傪帩偪婣傝丄巆傝
丂傪偍揦偱怘傋偨丅偙偺偲偒丄俀恖暘偺偍壻巕戙偼惻崬傒偱侾俁侽俉墌偩偭偨丅偍壻巕
丂侾屄偺惻敳偒偺抣抜偼偄偔傜偐丅偨偩偟丄徚旓惻偼丄偍揦偱怘傋傞応崌偼侾侽亾丄帩
丂偪婣傞応崌偼俉亾偐偐傞丅
乮夝乯丂俙丄俛偑偍揦偱怘傋偨偺偼寁侾俀屄丄帩偪婣偭偨偺傕寁侾俀屄側偺偱丄偍壻巕侾屄偺惻
丂丂丂敳偒偺抣抜傪俲偲偡傞偲丄
丂丂丂丂丂侾俀亊俲亊侾丏侾亄侾俀亊俲亊侾丏侽俉亖侾俁侽俉
丂傛偭偰丄丂侾俁丏俀俲亄侾俀丏俋俇俲亖侾俁侽俉丂傛傝丄丂俀俇丏侾俇俲亖侾俁侽俉丂丂側偺偱丄
丂丂俲亖俆侽丂丂乮廔乯
丂俹俛偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俀擭俀寧侾俀擔晅偗乯
丂彫妛惗偺偮傕傝偱夝偔側傜丏丏丏丅
丂俙丄俛偑偍揦偱怘傋偨偍壻巕傕帩偪婣偭偨偺傕侾俀屄側偺偱丄丂侾俁侽俉亐侾俀亖侾侽俋
丂偙傟偼丄俉亾偲侾侽亾偺惻嬥偑偐偐偭偨偍壻巕奺侾屄偺抣抜丄暯嬒偟偰丄俋亾偺惻嬥偑偐
偐偭偨偲峫偊偰丄
丂侾侽俋亐侾.侽俋亖侾侽侽丂偑偍壻巕俀屄偺抣抜丅丂傛偭偰丄偍壻巕侾屄偼丄俆侽墌
仸丂偙偺偲偒丄俉亾偺惻崬傒偱丄俆係墌丄侾侽亾偱偼丄俆俆墌偲側傝丄彫悢揰埲壓偑弌側偄偺偱丄
丂丂俙丄俛偑壗屄帩偪婣偭偰傕戣堄傪枮偨偡丅
丂 仸偺婰弎偼彫妛惗偵昁梫偱偟傚偆偐乧丅
乮僐儊儞僩乯丂偙偺栤戣愝掕偺応崌丄偍壻巕偼偡傋偰摨堦偺傕偺偱丄偟偐傕徚旓惻俉亾偺傕偺
丂丂丂丂丂丂偲徚旓惻侾侽亾偺傕偺偑摨悢偱偁傞偺偱丄俹俛偝傫偺傛偆側寁嶼偑惉棫偡傞偲巚偄
丂丂丂丂丂丂傑偡丅
乮捛婰乯丂椷榓俀擭搙嶗堻拞妛擖帋栤戣乮椷榓俀擭俀寧俀俈擔晅偗乯
俬丏乮俁乯丂傑偭偡偖側摴偵拰傪棫偰儘乕僾傪挘傝採摂傪捿傞偡丅拰偲拰偺娫偼俆倣俆侽們倣丄
丂丂丂丂採摂偲採摂偺娫偼侾倣俁俆們倣偱偁傞丅侾杮栚偺拰偐傜俁俆們倣棧傟偨偲偙傠偵侾屄
丂丂丂丂栚偺採摂傪捿傞偟偨丅儘乕僾偼偨傞傑側偄傕偺偲偟丄拰偺暆偼峫偊側偄丅
丂崱丄拰傪侾侽杮棫偰丄採摂傪捿傞偟偨丅師偺栤偄偵摎偊傛丅
乮侾乯丂採摂偼慡晹偱壗屄巊偭偨偐丅傑偨丄侾侽杮栚偺拰偵侾斣嬤偄採摂偼偦偺拰偐傜
丂丂壗們倣偺偲偙傠偵捿傞偟偨偐丅
乮俀乯丂拰偐傜俁俆們倣埲撪偺晹暘偵捿傞偟偨採摂偼庢傝奜偡偙偲偵偟偨丅偨偩偟丄侾屄栚
丂丂偺採摂偼奜偝側偄丅偙偺偲偒丄捿傞偝傟偨傑傑偺採摂偼壗屄偁傞偐丅
乮夝乯丂奊傪昤偄偰媮傔傞偲丄乮侾乯丂採摂偼俁俈屄偱丄侾侽杮栚偺拰偵侾斣嬤偄採摂偼偦偺拰
丂丂丂偐傜俆俆們倣偺偲偙傠偵捿傞偟偨丅
丂丂乮俀乯偼丄俁侽屄
丂丂寁嶼偱偼丄丂乮俆丏俆亊俋亅侽丏俁俆乯亐侾丏俁俆亖俁俇丒丒丒侽丏俆俆丂側偺偱丄採摂偺屄悢偼丄
丂俁俇亄侾亖俁俈屄偱丄嵟屻偺採摂偼丄侾侽杮栚偺拰傑偱丄俆俆們倣棧傟偰偄傞丅丂丂乮廔乯
嘦丏乮侾乯丂壓恾偺傛偆偵丄廲俀侽倣丄墶係侽倣偺挿曽宍偺椉僒僀僪偵捈宎俀侽倣偺敿墌傪
丂丂丂丂丂偮偗偨廃夞楬偑偁傞丅
丂丂丂丂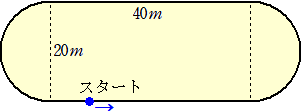
丂偙偺廃夞楬傪丄俙偼廃偺挿偝侾俆侽們値偺椫傪偙傠偑偟丄俛偼廃偺挿偝侾俀侽們値偺椫傪
偙傠偑偡丅椫偼妸傜側偄傕偺偲偡傞丅
乮僀乯丂俙偑偙偺廃夞楬傪侾廃偡傞偲丄椫偼壗夞揮偡傞偐丅
乮儘乯丂俙丄俛偑僗僞乕僩抧揰偐傜栴報偺岦偒偵丄椫傪侾昩娫偵侾夞揮偝偣側偑傜弌敪偟
丂丂偨丅搑拞丄俙偼俀夞僐乕僗傾僂僩偟丄僐乕僗偵栠傞傑偱寁係侽昩偐偐偭偨丅嵟屻丄俙丄俛
丂丂偼廃夞楬忋偺僑乕儖抧揰偵摨帪偵僑乕儖偟偨丅俙丄俛偼弌敪偟偰偐傜僑乕儖偡傞傑
丂丂偱壗廃偟偨偐丅
乮夝乯乮僀乯丂廃夞楬侾廃偼丄俀侽亊俁丏侾係亄俉侽亖侾係俀丏俉乮倣乯丂側偺偱丄
丂丂丂丂丂侾係俀丏俉亐侾丏俆亖俋俆丏俀乮夞揮乯
乮儘乯丂弌敪偟偰偐傜僑乕儖傑偱倲昩偐偐偭偨傕偺偲偡傞偲丄丂侾丏俀倲亖侾丏俆乮倲亅係侽乯丂傛傝丄
丂丂丂倲亖俀侽侽丂側偺偱丄憱峴嫍棧偼丄丂俀侽侽亊侾丏俀亖俀係侽乮倣乯
丂丂傛偭偰丄丂俀係侽亐侾係俀丏俉亖侾亄俉侾/侾侾俋乮廃乯丂丂乮廔乯
乮捛婰乯丂椷榓俀擭俀寧侾俈擔晅偗
丂俀侽俀侽擭侾寧侾俉擔乮搚乯偵峴傢傟偨撳拞妛峑偺擖帋栤戣乮侾擔栚乯偺師偺栤戣偵挧愴偟偰
傒傑偟偨丅
係丏丂枅擔媥傒側偔惢昳傪嶌偭偰偄傞岺応偑偁傞丅堦擔摉偨傝偵嶌傞惢昳偺屄悢偼丄
丂丂寧梛擔偐傜嬥梛擔傑偱偑摨偠偱丄搚梛擔偲擔梛擔偑摨偠偱丄搚梛擔偼嬥梛擔傛傝
丂丂彮側偄丅
丂偁傞擭丄偙偺岺応偱俇寧偵嶌偭偨惢昳偼俁俈俀屄丄俋寧偵嶌偭偨惢昳偼俁俇俇屄偱偁偭
偨丅偙偺擭偺俇寧侾擔偼壗梛擔偱偁傞偐丅傑偨丄偙偺擭偺俈寧偵嶌偭偨惢昳偼壗屄偱
偁傞偐丅
乮夝乯丂堦擔摉偨傝偵嶌傞惢昳偺屄悢傪丄搚梛擔偲擔梛擔偼倣屄丄寧梛擔偐傜嬥梛擔傑偱偼
丂丂丂値屄偲偡傞丅戣堄傛傝丄倣亙値偱偁傞丅
俇寧侾擔偑擔梛擔偲偡傞偲丄俋寧侾擔偼寧梛擔
丂俇寧偺寧乣嬥偼丄俀侾擔丄搚擔偼丄俋擔丄俋寧偺寧乣嬥偼丄俀俀擔丄搚擔偼丄俉擔
丂偙偺偲偒丄俇寧偵嶌偭偨惢昳偼丄俀侾値亄俋倣屄丄俋寧偵嶌偭偨惢昳偼丄俀俀値亄俉倣屄
丂丂丂俀侾値亄俋倣亖俁俈俀丂丄俀俀値亄俉倣亖俁俇俇丂傪枮偨偡夝偼側偄丅
俇寧侾擔偑寧梛擔偲偡傞偲丄俋寧侾擔偼壩梛擔
丂俇寧偺寧乣嬥偼丄俀俀擔丄搚擔偼丄俉擔丄俋寧偺寧乣嬥偼丄俀俀擔丄搚擔偼丄俉擔
丂戣堄傛傝丄偙偺応崌偼婲偙傝偊側偄丅
俇寧侾擔偑壩梛擔偲偡傞偲丄俋寧侾擔偼悈梛擔
丂俇寧偺寧乣嬥偼丄俀俀擔丄搚擔偼丄俉擔丄俋寧偺寧乣嬥偼丄俀俀擔丄搚擔偼丄俉擔
丂戣堄傛傝丄偙偺応崌偼婲偙傝偊側偄丅
俇寧侾擔偑悈梛擔偲偡傞偲丄俋寧侾擔偼栘梛擔
丂俇寧偺寧乣嬥偼丄俀俀擔丄搚擔偼丄俉擔丄俋寧偺寧乣嬥偼丄俀俀擔丄搚擔偼丄俉擔
丂戣堄傛傝丄偙偺応崌偼婲偙傝偊側偄丅
俇寧侾擔偑栘梛擔偲偡傞偲丄俋寧侾擔偼嬥梛擔
丂俇寧偺寧乣嬥偼丄俀俀擔丄搚擔偼丄俉擔丄俋寧偺寧乣嬥偼丄俀侾擔丄搚擔偼丄俋擔
丂偙偺偲偒丄俇寧偵嶌偭偨惢昳偼丄俀俀値亄俉倣屄丄俋寧偵嶌偭偨惢昳偼丄俀侾値亄俋倣屄
丂丂丂俀俀値亄俉倣亖俁俈俀丂丄俀侾値亄俋倣亖俁俇俇丂傪夝偔偲丄倣亖俉丄値亖侾係
俇寧侾擔偑嬥梛擔偲偡傞偲丄俋寧侾擔偼搚梛擔
丂俇寧偺寧乣嬥偼丄俀侾擔丄搚擔偼丄俋擔丄俋寧偺寧乣嬥偼丄俀侽擔丄搚擔偼丄侾侽擔
丂偙偺偲偒丄俇寧偵嶌偭偨惢昳偼丄俀侾値亄俋倣屄丄俋寧偵嶌偭偨惢昳偼丄俀侽値亄侾侽倣屄
丂丂丂俀侾値亄俋倣亖俁俈俀丂丄俀侽値亄侾侽倣亖俁俇俇丂傪枮偨偡夝偼側偄丅
俇寧侾擔偑搚梛擔偲偡傞偲丄俋寧侾擔偼擔梛擔
丂俇寧偺寧乣嬥偼丄俀侽擔丄搚擔偼丄侾侽擔丄俋寧偺寧乣嬥偼丄俀侾擔丄搚擔偼丄俋擔
丂偙偺偲偒丄俇寧偵嶌偭偨惢昳偼丄俀侽値亄侾侽倣屄丄俋寧偵嶌偭偨惢昳偼丄俀侾値亄俋倣屄
丂丂丂俀侽値亄侾侽倣亖俁俈俀丂丄俀侾値亄俋倣亖俁俇俇丂傪枮偨偡夝偼側偄丅
丂埲忋偐傜丄俇寧侾擔偼栘梛擔偱偁傞丅
丂偙偺偲偒丄俈寧偺寧乣嬥偼丄俀侾擔丄搚擔偼丄侾侽擔側偺偱丄惢昳偺屄悢偼丄
丂丂丂俀侾亊侾係亄侾侽亊俉亖俁俈係乮屄乯
乮僐儊儞僩乯丂慺杙偵夝偄偰偼傒偨傕偺偺帪娫偑偐偐傝偡偓傞丅傕偭偲忋庤偄夝朄偼側偄偺偩
丂丂丂丂丂丂傠偆偐丠偪側傒偵丄嬤擭偱俇寧侾擔偑栘梛擔偵側傞偺偼丄俀侽侾俈擭丅俁擭墇偟偺栤
丂丂丂丂丂丂戣嶌惉偩偭偨偺偩傠偆偐丠
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俀擭俀寧侾俉擔晅偗乯
丂6寧偲9寧偼30擔側偺偱丄搚擔偺擔悢偼8乣10丅
丂忦審偐傜搚擔偑彮側偄曽偑嶌傟傞惢昳偑懡偄偺偱丄俇寧偑372屄丄俋寧偑366屄偲偄偆偙偲
偐傜丄搚擔偺擔悢偼6寧偑8偐9丄9寧偑9偐10偱丄9寧偺曽偑搚擔偑懡偄丅
丂傛偭偰丄嵎偼1偐2偲側傝丄寧乣嬥偲搚擔偺惢昳偺屄悢偺嵎偼丄
丂搚擔偺擔悢偺嵎偑 1 偺偲偒丄丂(372-366)亐1=6丄 2 偺偲偒丄丂(372-366)亐2=3
丂搚擔偵惢昳偺屄悢偑彮側偄暘傪懌偡偲30偱妱傝愗傟側偗傟偽側傜側偄偑丄
丂丂372亄6亊8=420丂丄372亄6亊9=426丂丄372亄3亊8=396丂丄372亄3亊9=399
偐傜搚擔偺擔悢偺嵎偼丄1 偱丄搚擔偺擔悢偼丄6寧偑 8丄9寧偑 9 偲寛傑傞偺偱丄
丂6寧1擔偼栘梛擔丄9寧1擔偼嬥梛擔丅
丂寧乣嬥偺惢昳偺屄悢偼丄420亐30=14丄搚擔偺惢昳偺屄悢偼丄14-6=8丂偱偁傝丄7寧1擔偼
30亐7=28丒丒丒2丂偐傜丄搚梛擔偲側傝丄7寧偺搚擔偼10夞側偺偱丄7寧偺惢昳偺屄悢偼丄
丂14亊21+8亊10=374屄
乮僐儊儞僩乯丂搚擔偺擔悢偺嵎偵拲栚偡傞偲偙傠偵姶摦偟傑偟偨丅慡偰偺応崌傪栐梾偡傞昁梫
丂丂丂丂丂丂偑側偄傫偱偡偹両
丂DD++偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俀擭俀寧侾俉擔晅偗乯
丂6寧偐傜8寧傑偱偱丄92擔=13廡娫偲1擔側偺偱丄6寧2擔偲9寧1擔偑摨偠梛擔丄6寧3擔偲9寧
2擔偑摨偠梛擔丄丒丒丒丄6寧30擔偲9寧29擔偑摨偠梛擔偲側傝傑偡丅
丂偮傑傝丄嵎偺6屄偑弮悎偵6寧1擔偲9寧30擔偺嵎丄偲峫偊傟偽傕偭偲憗偄偱偟傚偆偐丅
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俀擭俀寧侾俉擔晅偗乯
丂偦傟偼柤埬両偲巚偄傑偟偨偑丄9寧30擔偑搚梛擔偐擔梛擔偐傪妋掕偡傞偨傔偵寢嬊寁嶼
偼昁梫側傢偗偱丄乽搚擔偺擔悢偺嵎偑2乿偺壜擻惈偑攔彍偝傟傞掱搙偱偟傚偆偐丅
丂夝摎傪嶌傞偙偲傪峫偊傞偲丄忋婰偺撪梕傪偁傞掱搙愢柧偟側偗傟偽側傝傑偣傫偺偱丄夝摎
偺暘検揑偵偼偁傑傝曄傢傜側偄傛偆側婥偑偟傑偡丅
丂DD++偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俀擭俀寧侾俉擔晅偗乯
丂撳拞擖帋偼寢壥偩偗偱傛偐偭偨傛偆側丅
丒6偮偺嵎偼寢嬊6寧1擔偲9寧30擔偺嵎
丒惗嶻悢偵6亊搚擔偺夞悢壛偊偨傜30偺攞悢乮偮傑傝堦偺埵偑0乯
丒6寧偺搚擔夞悢偼3夞偐8夞偐13夞偐乧乧忢幆揑偵8夞丄傛偭偰9寧偼9夞
丒9寧偺搚擔夞悢偑婏悢偲偄偆偙偲偼30擔偼搚梛偱丄梻擔梛偼傕偆10寧偩偭偨
丒偠傖偁6寧1擔偼梛擔傪2偮栠偭偰栘梛
偔傜偄偱摎偊傜傟傑偡偐偹丅
捛婰丗丂偁丄偱傕7寧偺惗嶻悢傪弌偡偨傔偵偼寢嬊寁嶼偑昁梫偐丅
乮捛婰乯丂椷榓俀擭俀寧俀俁擔晅偗
丂俀侽俀侽擭侾寧侾俋擔乮擔乯偵峴傢傟偨撳拞妛峑偺擖帋栤戣乮俀擔栚乯偺師偺栤戣偵挧愴偟偰
傒傑偟偨丅
係丏暯柺忋偵侾曈偺挿偝偑俇偺惓嶰妏宍俙俛俠偲拞怱俛偱敿宎俇偺墌偑偁傞丅偙偺墌傪
丂暯柺忋偱師偺傛偆偵堏摦偝偣傞偲偒丄墌偑捠夁偡傞晹暘偺柺愊傪媮傔傛丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮堦晹夵戣乯
丂丂丂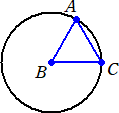
乮侾乯丂墌偺拞怱偑曈俛俠忋傪俛偐傜俠傑偱摦偔丅
乮俀乯丂墌偺拞怱偑曈俙俛忋傪俛偐傜俙傑偱摦偄偨屻丄曈俙俠忋傪俙偐傜俠傑偱摦偔丅
乮夝乯乮侾乯
 |
丂丂36兾亄12亊6亅乷乮36兾/6亅36 /4乯亊4亄乮36 /4乯亊4亄乮36 /4乯亊2乸 /4乯亊2乸
丂丂亖12兾亄72亄18 |
乮俀乯
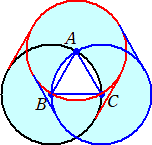 |
丂丂12兾亄72亄18 亄36兾/6亄36兾/2亅乮36兾/6亅36 亄36兾/6亄36兾/2亅乮36兾/6亅36 /4乯亊2 /4乯亊2
丂丂亖24兾亄72亄36 |
乮捛婰乯丂椷榓俀擭俀寧俀俆擔晅偗
丂俀侽俀侽擭侾寧侾俋擔乮擔乯偵峴傢傟偨撳拞妛峑偺擖帋栤戣乮俀擔栚乯偺師偺栤戣偵挧愴偟偰
傒傑偟偨丅
俀丏丂偙偺栤戣偱偼丄愭摢偵侽偑偁偭偰傕寘悢偵悢偊傞傕偺偲偡傞丅
乮侾乯丂峛偼俆寘偺悢俙俛俠俢傪巻偵彂偄偰壋偵搉偟偨丅偨偩偟丄俙丄俛丄俠丄俢丄俤偵摨偠
丂丂悢帤偑偁偭偰傕傛偄偲偡傞丅俤偼俙亄俛亄俠亄俢傪侾侽偱妱偭偨梋傝偱偁傞丅壋偼俙丄
丂丂俛丄俠丄俢丄俤偺拞偺侾屄傪暿偺悢帤偵彂偒姺偊偰暩偵搉偟偨丅暩偑庴偗庢偭偨悢
丂丂偼乽俀俉俋俈俁乿偱偁偭偨丅
乮傾乯丂峛偑巻偵彂偄偨偲峫偊傜傟傞俆寘偺悢傪偡傋偰彂偗丅
乮僀乯丂峛偼偼偠傔偲摨偠悢傪嵞傃巻偵彂偄偰壋偵搉偟偨丅壋偼俙丄俛丄俠丄俢丄俤偺偆偪
丂丂丂愭傎偳偲堎側傞侾屄傪暿偺悢帤偵彂偒姺偊偰暩偵搉偟偨丅暩偑庴偗庢偭偨悢偼
丂丂丂乽俀侾俇俈俁乿偱偁偭偨丅峛偑巻偵彂偄偨偲峫偊傜傟傞俆寘偺悢傪媮傔傛丅
乮俀乯丂懢榊偝傫偼俇寘偺悢俹俻俼俽俿倀傪巻偵彂偄偰壋偵搉偟偨丅偨偩偟丄俹丄俻丄俼丄俽丄
丂丂丂俿丄倀偵摨偠悢帤偑偁偭偰傕傛偄偲偡傞丅傑偨丄俿偼俹亄俻亄俼亄俽傪侾侽偱妱偭偨
丂丂丂梋傝偱丄倀偼俹亄俻亊俁亄俼亊俈亄俽亊俋傪侾侽偱妱偭偨梋傝偱偁傞丅
丂
丂丂壋偼俹丄俻丄俼丄俽丄俿丄倀偺拞偺侾屄傪暿偺悢帤偵彂偒姺偊偰暩偵搉偟偨丅暩偑庴偗
丂丂庢偭偨悢偼乽俈俁俆俇俁侾乿偱偁偭偨丅峛偑巻偵彂偄偨偲峫偊傜傟傞俇寘偺悢傪媮傔傛丅
乮夝乯乮侾乯乮傾乯丂壜擻惈偼師偺俆捠傝
丂丂丂倃俉俋俈俁丒丒丒丂倃亄俉亄俋亄俈亖倃亄俀係傪侾侽偱妱偭偨梋傝偑俁偲側傞偺偱丄丂倃亖俋
丂丂丂丂丂丂丂丂丂丂丂傛偭偰丄俋俉俋俈俁
丂丂丂俀倃俋俈俁丒丒丒丂俀亄倃亄俋亄俈亖倃亄侾俉傪侾侽偱妱偭偨梋傝偑俁偲側傞偺偱丄丂倃亖俆
丂丂丂丂丂丂丂丂丂丂丂傛偭偰丄俀俆俋俈俁
丂丂丂俀俉倃俈俁丒丒丒丂俀亄俉亄倃亄俈亖倃亄侾俈傪侾侽偱妱偭偨梋傝偑俁偲側傞偺偱丄丂倃亖俇
丂丂丂丂丂丂丂丂丂丂丂傛偭偰丄俀俉俇俈俁
丂丂丂俀俉俋倃俁丒丒丒丂俀亄俉亄俋亄倃亖倃亄侾俋傪侾侽偱妱偭偨梋傝偑俁偲側傞偺偱丄丂倃亖係
丂丂丂丂丂丂丂丂丂丂丂傛偭偰丄俀俉俋係俁
丂丂丂俀俉俋俈倃丒丒丒丂俀亄俉亄俋亄俈亖俀俇傪侾侽偱妱偭偨梋傝偑俇偲側傞偺偱丄丂俀俉俋俈俇
乮僀乯丂俀侾俇俈俁偲侾帤堘偄偼丄丂俀俉俇俈俁
乮俀乯丂壜擻惈偼師偺俇捠傝
丂丂丂倃俁俆俇俁侾丒丒丒倃亄俁亄俆亄俇亖倃亄侾係佭俁仺倃亖俋
丂丂丂丂丂丂丂丂丂丂丂偙偺偲偒丄俋亄俁丒俁亄俆丒俈亄俇丒俋亖侾侽俈佭俈偱柕弬
丂丂丂俈倃俆俇俁侾丒丒丒俈亄倃亄俆亄俇亖倃亄侾俉佭俁仺倃亖俆
丂丂丂丂丂丂丂丂丂丂丂偙偺偲偒丄俈亄俆丒俁亄俆丒俈亄俇丒俋亖侾侾侾佭侾偱揔
丂丂丂俈俁倃俇俁侾丒丒丒俈亄俁亄倃亄俇亖倃亄侾俇佭俁仺倃亖俈
丂丂丂丂丂丂丂丂丂丂丂偙偺偲偒丄俈亄俁丒俁亄俈丒俈亄俇丒俋亖侾侾俋佭俋偱柕弬
丂丂丂俈俁俆倃俁侾丒丒丒俈亄俁亄俆亄倃亖倃亄侾俆佭俁仺倃亖俉
丂丂丂丂丂丂丂丂丂丂丂偙偺偲偒丄俈亄俁丒俁亄俆丒俈亄俉丒俋亖侾俀俁佭俁偱柕弬
丂丂丂俈俁俆俇倃侾丒丒丒俈亄俁亄俆亄俇亖俀侾佭侾仺倃亖侾
丂丂丂丂丂丂丂丂丂丂丂偙偺偲偒丄俈亄俁丒俁亄俆丒俈亄俇丒俋亖侾侽俆佭俆偱柕弬
丂丂丂俈俁俆俇俁倃丒丒丒俈亄俁亄俆亄俇亖俀侾佭侾偱柕弬
丂丂埲忋偐傜丄丂俈俆俆俇俁侾
乮捛婰乯丂椷榓俀擭俀寧俀俋擔晅偗
丂俀侽俀侽擭侾寧侾俋擔乮擔乯偵峴傢傟偨撳拞妛峑偺擖帋栤戣乮俀擔栚乯偺師偺栤戣偵挧愴偟偰
傒傑偟偨丅
俁丏丂俀係帪娫昞帵偺僨僕僞儖帪寁偑偁傞丅偙偺帪寁傪俀係帪娫摦偐偟偨偲偒丄師偺忦審
丂丂傪枮偨偡昞帵偑偝傟偰偄傞帪娫偼丄崌傢偣偰壗暘娫偐丅偨偩偟丄昞帵偑曄傢傞偺
丂丂偵偐偐傞帪娫偼峫偊側偄傕偺偲偡傞丅
乮侾乯丂係偮偺悢帤偺偆偪丄俀偑偪傚偆偳俁偮偁傞
乮俀乯丂係偮偺悢帤偺偆偪丄俀偑偪傚偆偳俀偮偁傞
乮俁乯丂係偮偺悢帤偺偆偪丄俀偑偪傚偆偳侾偮偁傞
乮夝乯乮侾乯丂**丗**丂偱丄俀俀丗俀*丂偺僞僀僾偼丄俋捠傝丂丄俀俀丗*俀丂偺僞僀僾偼丄俆捠傝
丂丂丂丂丂丂俀*丗俀俀丂偺僞僀僾偼丄丂俁捠傝丂丄*俀丗俀俀丂偺僞僀僾偼丄俀捠傝
丂丂丂丂丂埲忋偐傜丄媮傔傞応崌偺悢偼丄丂俋亄俆亄俁亄俀亖侾俋乮捠傝乯
乮俀乯丂俀俀丗**丂偺僞僀僾偼丄俆亊俋亖係俆乮捠傝乯丂丄俀*丗俀*丂偺僞僀僾偼丄俁亊俋亖俀俈乮捠傝乯
丂丂俀*丗*俀丂偺僞僀僾偼丄丂俁亊俆亖侾俆乮捠傝乯丂丄*俀丗俀*丂偺僞僀僾偼丄俀亊俋亖侾俉乮捠傝乯
丂丂*俀丗*俀丂偺僞僀僾偼丄俀亊俆亖侾侽乮捠傝乯丂丄**丗俀俀丂偺僞僀僾偼丄俀亊俋亖侾俉乮捠傝乯
丂埲忋偐傜丄媮傔傞応崌偺悢偼丄丂係俆亄俀俈亄侾俆亄侾俉亄侾侽亄侾俉亖侾俁俁乮捠傝乯
乮俁乯丂俀*丗**丂偺僞僀僾偼丄俁亊俆亊俋亖侾俁俆乮捠傝乯丄*俀丗**丂偺僞僀僾偼丄俀亊俆亊俋亖俋侽乮捠傝乯
丂丂**丗俀*丂偺僞僀僾偼丄俀亊俋亊俋亖侾俇俀乮捠傝乯丄**丗*俀丂偺僞僀僾偼丄俀亊俋亊俆亖俋侽乮捠傝乯
丂埲忋偐傜丄媮傔傞応崌偺悢偼丄丂侾俁俆亄俋侽亄侾俇俀亄俋侽亖係俈俈乮捠傝乯
乮捛婰乯丂椷榓俀擭俁寧侾俋擔晅偗
丂戝嶃惎岝妛堾拞妛峑乮俀侽俀侽乯偺擖帋栤戣偵挧愴偟偰傒傑偟偨丅
侾丏乮係乯丂偄偔偮偐偺晹壆偵惗搆傪擖傟傞偺偵丄係恖偢偮偵偡傞偲俈恖偑擖傟側偔側傝丄
丂丂丂丂俇恖偢偮偵偡傞偲係晹壆梋傝傑偡丅
丂丂丂丂偙偺偲偒丄峫偊傜傟傞惗搆偺悢傪偡傋偰媮傔傛丅
乮夝乯丂惗搆偺恖悢傪俶丄晹壆偺悢傪俵偲偡傞偲丄戣堄傛傝丄
丂丂丂俶亅係俵亖俈丂丄俇乮俵亅俆乯亙俶亝俇乮俵亅係乯丂側偺偱丄俇乮俵亅俆乯亙係俵亄俈亝俇乮俵亅係乯
丂傛偭偰丄丂俀俵亙俁俈丂偐偮丂俀俵亞俁侾丂傛傝丄丂侾俇亝俵亝侾俉丂側偺偱丄丂俵亖侾俇丄侾俈丄侾俉
丂偙偺偲偒丄丂俶亖俈侾丄俈俆丄俈俋丂丂乮廔乯
乮捛婰乯丂椷榓俀擭俁寧俀侽擔晅偗
丂惣戝榓妛墍拞妛峑乮俀侽俀侽乯偺擖帋栤戣偵挧愴偟偰傒傑偟偨丅
侾丏乮俁乯丂偁傞巇帠偼丄俙偝傫偲俛偝傫偺俀恖偱峴偆偲丄偪傚偆偳侾俉擔娫偱廔傢傞梊掕偱
丂丂丂丂丂偟偨丅偲偙傠偑丄搑拞偱俛偝傫偩偗偑晽幾偱俆擔娫媥傫偩偺偱丄巇帠傪廔偊傞
丂丂丂丂丂偺偵偪傚偆偳俀侽擔娫偐偐偭偰偟傑偄傑偟偨丅
丂丂丂丂丂偙偺巇帠偼丄俛偝傫侾恖偩偗偱傗傞偲偡傟偽丄偪傚偆偳壗擔娫偱廔傢傝傑偡偐丠
乮夝乯丂俙偝傫偲俛偝傫偺侾擔摉偨傝偺巇帠検傪倶丄倷偲偍偔偲丄侾俉倶亄侾俉倷亖侾丄俀侽倶亄侾俆倷亖侾
丂侾俉倶亄侾俉倷亖俀侽倶亄侾俆倷丂傛傝丄丂俁倷亖俀倶丂側偺偱丄丂倷亖俀倶/俁丂傪丂侾俉倶亄侾俉倷亖侾丂偵
戙擖偟偰丄丂侾俉倶亄侾俀倶亖侾丂傛偭偰丄丂倶亖侾/俁侽丂偱丄丂倷亖侾/係俆
丂偟偨偑偭偰丄俛偝傫侾恖偩偗偱傗傞偲偡傟偽丄侾亐乮侾/係俆乯亖係俆乮擔娫乯丂偱廔傢傞丅丂丂乮廔乯
乮僐儊儞僩乯丂曽掱幃傪棫幃偡傟偽梕堈偩偑丄彫妛惗偼偳偆夝偔偺偩傠偆丅
丂DD++偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俀擭俁寧俀侾擔晅偗乯
丂彫妛惗側傜偙偆偐側丠
丂A偝傫偑18擔丄B偝傫偑18擔摥偄偰廔傢傞巇帠偑丄A偝傫偑20擔丄B偝傫偑15擔摥偄偰廔傢
傞偲偄偆偙偲偼丄A偝傫偑2擔偱傗傞巇帠偲B偝傫偑3擔偱傗傞巇帠偼摨偠検偲偄偆偙偲偵側傝傑
偡丅偮傑傝丄A偝傫偑20擔偱傗傞巇帠偼B偝傫側傜30擔偐偐傞偺偱丄摎偊偼丄15+30=45擔
乮僐儊儞僩乯丂俛偝傫偑摥偄偨擔悢偼丄侾俉亅俆亖侾俁丂偱偼側偔偰丄俀侽亅俆亖侾俆丂側傫偱偡偹両
丂丂丂丂丂丂姩堘偄偟偰偄傑偟偨丅DD++偝傫偵姶幱偟傑偡丅
俀丏乮俁乯丂壓恾偺暯峴巐曈宍俙俛俠俢偵偍偄偰丄俙俹丗俹俛亖俀丗侾丄俛俻丗俻俠亖俁丗侾丄揰俼
丂丂丂丂丂偼曈俠俢偺拞揰偱偁傞丅俢俹偲俙俻丄俙俼偲岎傢傞揰傪偦傟偧傟俽丄俿偲偡傞偲偒丄
丂丂丂丂丂俹俽丗俿俢傪傕偭偲傕娙扨側惍悢斾偱昞偣丅
丂丂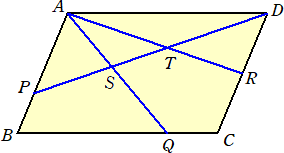
乮夝乯丂師偺傛偆側恾傪峫偊傞丅
丂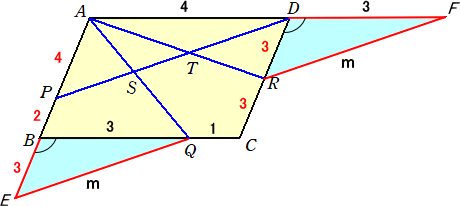
丂偙偺偲偒丄俹俽亖係倣/俋丄俿俢亖係倣/俈丂側偺偱丄俹俽丗俿俢亖係倣/俋丗係倣/俈亖俈丗俋丂丂乮廔乯
乮僐儊儞僩乯丂掕斣拞偺掕斣偺栤戣偱偡偑丄彫妛惗偼偳偆夝偄偨偺偩傠偆丠
乮捛婰乯丂椷榓俀擭俁寧俀俋擔晅偗
丂塰岝妛墍拞妛峑乮俀侽俀侽乯偺擖帋栤戣偵挧愴偟偰傒傑偟偨丅
侾丏丂侾偐傜偁傞悢傑偱偺偡傋偰偺惍悢偺拞偐傜侾偮偩偗庢傝彍偒丄巆偭偨惍悢傪峫偊
丂丂傞丅師偺栤偵摎偊傛丅
乮侾乯丂侾偐傜侾侽侽傑偱偺惍悢偺拞偐傜侾偮偩偗庢傝彍偄偨丅巆偭偨惍悢偺暯嬒偼丄
丂丂丂俆俆係/侾侾偵側偭偨丅庢傝彍偄偨惍悢傪摎偊傛丅
乮俀乯丂侾偐傜偁傞悢傑偱偺惍悢偺拞偐傜侾偮偩偗庢傝彍偒丄巆偭偨惍悢偺榓偼丄俇侽侽
丂丂丂偵側偭偨丅庢傝彍偄偨惍悢傪摎偊傛丅
乮俁乯丂侾偐傜偁傞悢傑偱偺惍悢偺拞偐傜侾偮偩偗庢傝彍偒丄巆偭偨惍悢偺暯嬒偼丄
丂丂丂係係侽/侾俁偵側偭偨丅庢傝彍偄偨惍悢傪摎偊傛丅
乮夝乯乮侾乯丂巆偭偨惍悢偺榓偼丄丂乮俆俆係/侾侾乯亊俋俋亖係俋俉俇
丂丂丂丂丂堦曽丄侾偐傜侾侽侽傑偱偺惍悢偺榓偼丄丂侾侽侽亊侾侽侾/俀亖俆侽俆侽
丂丂丂丂丂傛偭偰丄庢傝彍偄偨惍悢偼丄丂俆侽俆侽亅係俋俉俇亖俇係
乮俀乯丂乮侾亄俀亄丒丒丒亄俵乯亅俶亖俇侽侽丂傛傝丄丂俵乮俵亄侾乯/俀亅俶亖俇侽侽
丂丂丂丂偙偺偲偒丄丂侾亝俵乮俵亄侾乯/俀亅俇侽侽亝俵丂傪枮偨偡俵偼丄俁俆偺傒丅
丂丂丂丂丂傛偭偰丄丂俶亖俵乮俵亄侾乯/俀亅俇侽侽亖俇俁侽亅俇侽侽亖俁侽
乮俁乯丂乷乮侾亄俀亄丒丒丒亄俵乯亅俶乸/乮俵亅侾乯亖係係侽/侾俁丂傛傝丄
丂丂丂丂侾亝俵乮俵亄侾乯/俀亅乮係係侽/侾俁乯乮俵亅侾乯亝俵
丂忋幃傪枮偨偡俵偼丄丂俇俇丂傑偨偼丂俇俈
丂俵亖俇俇偺偲偒丄丂俀俀侾侾亅俶亖乮係係侽/侾俁乯亊俇俆亖俀俀侽侽丂傛傝丄丂俶亖侾侾
丂俵亖俇俈偺偲偒丄丂俀俀俈俉亅俶亖乮係係侽/侾俁乯亊俇俇丂偱丄偙偺幃傪枮偨偡惍悢俶偼懚嵼偟側偄丅
乮僐儊儞僩乯丂乮侾乯偼壗偱傕側偄偑丄暯曽崻偺寁嶼摍偱丄乮俀乯乮俁乯偱偼寁嶼婡偺偍悽榖偵側偭偨丅
丂丂丂丂丂丂彫妛惗偼偳偆夝偄偨偺偩傠偆丠
乮捛婰乯丂椷榓俀擭俁寧俁侾擔晅偗
丂俀侽俀侽擭侾寧侾俉擔乮搚乯偵峴傢傟偨撳拞妛峑偺擖帋栤戣乮侾擔栚乯偺師偺栤戣偵挧愴偟偰
傒傑偟偨丅
俈丏丂壓恾偺傛偆側暯峴巐曈宍俙俛俠俢偵偍偄偰丄俛俧丗俧俢亖俆丗俈丄俥俧亖侾偲偡傞丅
丂丂偙偺偲偒丄俤俥偺挿偝傪媮傔傛丅
丂丂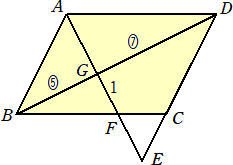
乮夝乯丂仮俙俛俧佷仮俤俢俧丂傛傝丄丂俙俧丟俤俧亖俆丗俈丂丄俙俛丗俤俢亖俆丗俈
丂丂丂傛偭偰丄丂俢俠丗俠俤亖俆丗俀
丂丂丂俙俢偲俥俠偼暯峴側偺偱丄丂俙俥丟俥俤亖俢俠丗俠俤亖俆丗俀
丂偙偙偱丄俤俥亖倶丂偲偍偔偲丄丂俙俧亖乮俆/俈乯俤俧亖乮俆/俈乯乮倶亄侾乯丂側偺偱丄
丂乮俆/俈乯乮倶亄侾乯亄侾丗倶亖俆丗俀丂傛傝丄丂俆倶亖乮侾侽/俈乯乮倶亄侾乯亄俀
丂偙傟傪夝偄偰丄丂倶亖俀係/俀俆丂丂乮廔乯
乮僐儊儞僩乯丂曽掱幃傪棫偰偰夝偄偨偑丄彫妛惗偼偳偺傛偆偵夝偔偺偩傠偆丠
丂拞妛庴尡偺昿弌栤戣偺傛偆偱丄庴尡惗偼師偺傛偆偵夝偔傜偟偄偱偡丅
丂壓恾偺傛偆側悢捈慄傪峫偊丄俆亄俈亖侾俀偲俆亄俀亖俈偺嵟彫岞攞悢俉係偑丄恾拞偺愒悢帤
偺傛偆偵丄俙俧丗俧俥丗俥俤亖俁俆丗俀俆丗俀係丂偲暘妱偝傟傞丅
丂俥俧亖侾丂側偺偱丄丂俤俥亖俀係/俀俆丂偑恾偐傜撉傒庢傟傞丅
丂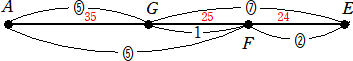
乮捛婰乯丂椷榓俀擭係寧侾擔晅偗
丂廰扟嫵堢妛墍廰扟拞妛峑乮俀侽俀侽乯偺擖帋栤戣偵挧愴偟偰傒傑偟偨丅
侾丏乮俀乯丂偁傞俀寘偺惍悢偲俀侽俀侽偺愊偼丄奺埵偺悢偑侽偲侾偺傒偺惍悢偱偡丅
偁傞俀寘偺惍悢偺偆偪嵟傕戝偒偄惍悢偼偄偔偮偱偡偐丅
乮夝乯丂俀侽俀侽亖俀2亊俆亊侾侽侾亖俀亊侾侽侾侽丂偲峫偊傞偲丄
丂丂丂俆亊俀亊侾侽侾侽亊侾侾亖侾侾侾侾侽侽
丂偲偡傟偽丄忦審傪枮偨偡丅傛偭偰丄媮傔傞惍悢偼丄丂俆俆丂丂乮廔乯
乮僐儊儞僩乯丂夝摎偵愢摼椡偑姶偠傜傟側偄偺偱丄偁傑傝帺怣偑偁傝傑偣傫丅偙傟埲奜偺夝摎
丂丂丂丂丂丂偼側偄傕偺偱偟傚偆偐丠
丂DD++偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俀擭係寧侾擔晅偗乯
丂傑偢丄2020偼10偺攞悢側偺偱丄乽2寘偺惍悢乿偲偺愊傕10偺攞悢偱偡丅傛偭偰丄堦偺埵偺悢
帤偼0偱偡丅
丂偦傟傪庢傝彍偄偨悢丄偡側傢偪丄乽2寘偺惍悢乿偲202偺愊傕0偲1偩偗偱彂偗傞悢偱偁傝丄202
偑嬼悢偱偁傞偙偲偐傜丄堦偺埵乮尦乆偺廫偺埵乯偼丄0偱偡丅傛偭偰丄乽2寘偺惍悢乿偼丄5偺攞悢
偱偡丅
丂偝傜偵丄枛旜偺0傪庢傝彍偄偨悢丄偡側傢偪乽2寘偺惍悢偺1/5乿偲101偺愊傕0偲1偩偗偱彂偗
傞悢偱偡丅
丂偲偙傠偱丄乽2寘偺惍悢偺1/5乿偼丄2埲忋19埲壓偺惍悢側偺偱丄101傪偐偗傞偲偒偵孞傝忋偑
傝偑愨懳偵敪惗偟傑偣傫丅偮傑傝丄乽2寘偺惍悢偺1/5乿帺懱偑0偲1偩偗偱彂偗傞悢丄偮傑傝丄
10偐11偲偄偆偙偲偵側傝傑偡丅
丂偟偨偑偭偰丄尦偺乽2寘偺惍悢乿偼丄50偐55丄嵟戝偺傕偺傪摎偊傞側傜丄55偲偄偆偙偲偵側傝傑
偡丅
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俀擭係寧侾擔晅偗乯
丂2020亊100=202000側偺偱丄奺埵偺悢偑0偲1偺傒偱偁傞惍悢偼111111埲壓丅
111111亐2020=55丂梋傝 11丂偐傜丄111100亐2020=55丂偲傢偐傞偺偱丄摎偊偼丄55
乮僐儊儞僩乯丂側傞傎偳両榑棟揑偱愢摼椡偁傞愢柧偵姶幱偟傑偡丅DD++偝傫丄傜偡偐傞偝傫丄偁
丂丂丂丂丂丂傝偑偲偆偛偞偄傑偟偨丅
乮捛婰乯丂椷榓俁擭俀寧侾侽擔晅偗
丂椷榓俁擭俀寧俇擔乮搚乯晅偗挬擔怴暦挬姧偵椷榓俁擭搙奐惉拞妛擖帋栤戣偑宖嵹偝傟偨丅
偄偔偮偐柺敀偦偆側栤戣偑偁偭偨偺偱丄彫妛惗偵側偭偨偮傕傝偱峫偊偰傒偨丅
侾丏乮侾乯俀侽俀侾擭俀寧侾擔偼寧梛擔偱偁傞丅侾侽侽擭屻偺俀侾俀侾擭俀寧侾擔偼壗梛擔偐丠
乮夝乯丂侾侽侽擭娫偺偆偪丄偆傞偆擭偼丄侾侽侽亐係亅侾亖俀係乮夞乯
丂丂丂乮俀侾侽侽擭偼侾侽侽偺攞悢偩偑係侽侽偺攞悢偱側偄偺偱丄偆傞擭偱偼側偄偐傜侾尭乯
丂丂巆傝偺俈俇夞偼暯擭偱偁傞丅
丂傛偭偰丄丂俀係亊俁俇俇亄俈俇亊俁俇俆亄侾佭俇丂乮倣倧倓丂俈乯丂傛傝丄搚梛擔偱偁傞丅丂丂乮廔乯
侾丏乮俀乯丂嶰妏宍偺奺捀揰偐傜岦偐偄崌偆曈偵丄捈慄傪偦傟偧傟俀杮丄俁杮丄侾侽侽杮
丂丂丂丂堷偄偨偲偒丄尦偺嶰妏宍偼壗屄偺晹暘偵暘偗傜傟傞偐丅偨偩偟丄俁杮埲忋偺
丂丂丂丂捈慄偑嶰妏宍偺撪晹偺侾揰偱岎傢傞偙偲偼側偄傕偺偲偡傞丅
丂傑偢帋偟偵幚尡偟偰丄夝朄偺庤弴傪扵傠偆丅
 |
乮夝乯丂傑偢丄俀捀揰偐傜捈慄傪偦傟偧傟俀杮丄俁杮堷偄偨
丂丂嶰妏宍偵偍偄偰丄悢偊傞偲丄侾俀屄偺晹暘偵暘偐傟傞
丂丂偙偲偑暘偐傞丅巆傝偺捀揰偐傜捈慄傪侾杮堷偄偨恾
丂丂偑壓恾偱偁傞丅 |
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂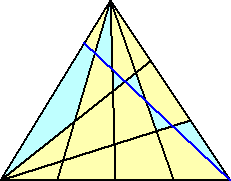 |
丂忋恾偐傜丄嶰妏宍偼丄侾俉屄偺晹暘偵暘偐傟傞丅挌搙丄俇屄憹偊偰偄傞偑丄偙傟偼俆杮偺捈
慄偲嵟屻偵堷偄偨捈慄偑俆揰偱岎傢傝丄偦偺岎揰偱捈慄偑俇暘妱偝傟丄偦偺暘妱偺偦傟偧傟
偑侾偮偢偮怴偟偄晹暘傪嶌傞偐傜偱偁傞丅偙偺惈幙偼丄戞俁偺捀揰偐傜捈慄傪堷偔尷傝晄曄側
惈幙偱偁傞丅
丂丂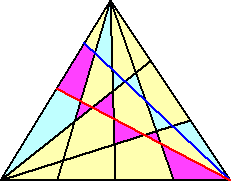
丂傛偭偰丄戞俁偺捀揰偐傜捈慄傪侾侽侽杮堷偄偨応崌丄晹暘偺憤悢偼丄
丂侾俀亄俇亊侾侽侽亖俇侾俀乮屄乯丂偱偁傞丅丂丂乮廔乯
乮捛婰乯丂椷榓係擭係寧侾俋擔晅偗
丂椷榓俁擭搙偺奐惉拞妛擖帋栤戣偺懕偒偱偡丅栤戣偼堦晹夵戣偟偰偁傝傑偡丅
侾丏乮係乯丂侾/俋俋俋俉 傪彫悢偱昞偡偲偒丄彫悢戞係俉埵偺悢丄彫悢戞俆俇埵偺悢傪偦傟偧
丂丂丂丂丂傟媮傔傛丅
丂侾/俋俋俋俉傪彫悢偱昞偡偲偒丄彫悢戞係俉埵偺悢傪媮傔傛丄偲偄偆塤傪捦傓傛偆側栤戣偱偡偑
拤幚偵戣堄偵廬偭偰寁嶼偡傟偽妶楬偑傂傜偗傞栤戣偱偡丅
丂庤尦偵揹戩偑偁傟偽丄
丂1/9998
=0丏0001000200 0400080016 0032006401 2802560512 1024204840 9681936387
丂丂2774554910 9821964392 8785757151 4302860572 1144228845 7691538307 6615323乧
偲彫悢揥奐偱偒傞偺偱丄彫悢戞係俉埵偺悢偼 俉丄彫悢戞俆俇埵偺悢偼 俁偲偡偖暘偐傝傑偡偑丄
偙傟傪庤寁嶼偱偳偆偧両偲偄偆栤戣偱偡丅
乮夝乯丂1/9998亖1/乮10000亅2乯亖乮1/10000乯丒乮侾/乮侾亅2/10000乯丂傛傝丄
1/9998
亖乮1/10000乯丒乮侾亄乮2/10000乯亄乮2/10000乯2亄乮2/10000乯3亄乮2/10000乯4亄丒丒丒乯
亖0丏0001丂丂乮仼丂彫悢戞係埵傑偱乯
亄0丏00000002丂丂乮仼丂彫悢戞俉埵傑偱乯
亄0丏000000000004丂丂乮仼丂彫悢戞侾俀埵傑偱乯
亄0丏0000000000000008丂丂乮仼丂彫悢戞侾俇埵傑偱乯
亄0丏.00000000000000000016丂丂乮仼丂彫悢戞俀侽埵傑偱乯
亄0丏000000000000000000000032丂丂乮仼丂彫悢戞俀係埵傑偱乯
丂丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒
丂傛偭偰丄彫悢戞係俉埵傪媮傔傞偵偼丄丂係俉亐係亖侾俀丂偐傜丄丂俀^(12-1)亖俀侽係俉丂偺堦偺埵
俉偑摎偲側傞丅
丂彫悢戞俆俇埵傪媮傔傞偵偼丄俆俇亐係亖侾係丂偐傜丄俀^(14-1)亖俉侾俋俀丂偺堦偺埵俀偵懳偟偰丄
彫悢戞俇侽埵偵憡摉偡傞悢傪媮傔偰丄丂俇侽亐係亖侾俆丂偐傜丄丂俀^(15-1)亖侾俇俁俉係丂側偺偱丄
偦偺枩偺埵傪壛枴偟側偗傟偽側傜側偄丅
亄0丏00000000丒丒丒丒丒丒丒丒丒丒00008192
亄0丏00000000丒丒丒丒丒丒丒丒丒丒000000016384
丂傛偭偰丄媮傔傞悢偼丄丂俀亄侾亖俁丂偱偁傞丅
乮捛婰乯丂椷榓俁擭俁寧侾俈擔晅偗
丂椷榓俁擭俀寧俆擔乮嬥乯晅偗挬擔怴暦挬姧偵椷榓俁擭搙嶗堻拞妛擖帋栤戣偑宖嵹偝傟偨丅
偄偔偮偐柺敀偦偆側栤戣偑偁偭偨偺偱丄彫妛惗偵側偭偨偮傕傝偱峫偊偰傒偨丅
侾丏乮俁乯丂惍悢倃偺栺悢偺偆偪丄侾埲奜偺栺悢偺屄悢傪亂倃亃丄侾埲奜偺栺悢偺榓傪亙倃亜偲
丂丂丂丂丂昞偡丅
乮侾乯丂亙俙亜亐亂俙亃偑惍悢偵側傜側偄俀寘偺惍悢俙偺偆偪丄嵟戝偺傕偺傪媮傔傛丅
乮夝乯丂俀寘偺惍悢俋俋丄俋俉丄俋俈丄俋俇丄丒丒丒丂傪弴師挷傋傞丅
丂俋俋亖俁2丒侾侾丂側偺偱丄丂亙俋俋亜亖乮侾亄俁亄俋乯乮侾亄侾侾乯亅侾亖侾俆俆
丂丂丂丂亂俋俋亃亖俁亊俀亅侾亖俆丂傛傝丄亙俙亜亐亂俙亃偑惍悢
丂俋俉亖俀丒俈2丂側偺偱丄丂亙俋俉亜亖乮侾亄俀乯乮侾亄俈亄係俋乯亅侾亖侾俈侽
丂丂丂丂亂俋俉亃亖俀亊俁亅侾亖俆丂傛傝丄亙俙亜亐亂俙亃偑惍悢
丂俋俈偼慺悢側偺偱丄丂亙俋俈亜亖俋俈亅侾亖俋俇
丂丂丂丂亂俋俈亃亖俀亅侾亖侾丂傛傝丄亙俙亜亐亂俙亃偑惍悢
丂俋俇亖俀5丒俁丂側偺偱丄丂亙俋俇亜亖乮侾亄俀亄係亄俉亄侾俇亄俁俀乯乮侾亄俁乯亅侾亖俀俆侾
丂丂丂丂亂俋俇亃亖俇亊俀亅侾亖侾侾丂傛傝丄亙俙亜亐亂俙亃偑惍悢偵側傜側偄
丂傛偭偰丄媮傔傞惍悢俙偼丄俋俇丂丂乮廔乯
乮俀乯丂亂俛亃亖俀丄亙俛亜亖侾係侽俇丂偺偲偒丄俛傪媮傔傛丅
乮夝乯丂亂俛亃亖俀丂傛傝丄侾傪娷傔偨栺悢偺屄悢偼丄俁丂側偺偱丄丂俛亖倫2丂乮倫偼慺悢乯
丂丂丂偙偺偲偒丄丂亙俛亜亖倫亄倫2亖侾係侽俇
丂丂乮倫亅俁俈乯乮倫亄俁俉乯亖侽丂傛傝丄丂倫亖俁俈丂丂傛偭偰丄丂俛亖俁俈2亖侾俁俇俋丂丂乮廔乯
乮俁乯丂俠亖俀10丂偺偲偒丄丂亂俠亃傪媮傔傛丅
乮夝乯丂亂俠亃亖侾侽亄侾亅侾亖侾侽丂丂乮廔乯
乮係乯丂俇侽埲壓偺惍悢偺偆偪丄亂俢亃亖俁丂偲側傞惍悢俢偼慡晹偱壗屄偁傞偐丅
乮夝乯丂亂俢亃亖俁丂偲側傞偨傔偵偼丄惍悢俢偼丄
丂丂俢亖倫3丂乮倫偼慺悢乯丂傑偨偼丄丂俢亖倫倯丂乮倫丄倯偼慺悢乯
丂俢亖倫3丂乮倫偼慺悢乯偺偲偒丄丂倫亖俀丄俁丂偺俀捠傝
丂俢亖倫倯丂乮倫丄倯偼慺悢乯偺偲偒丄
丂丂乮倫丆倯乯亖乮俀丆俁乯丄乮俀丆俆乯丄乮俀丆俈乯丄乮俀丆侾侾乯丄乮俀丆侾俁乯丄乮俀丆侾俈乯丄乮俀丆侾俋乯丄乮俀丆俀俁乯丄
丂丂丂丂丂丂丂丂乮俀丆俀俋乯丄乮俁丆俆乯丄乮俁丆俈乯丄乮俁丆侾侾乯丄乮俁丆侾俁乯丄乮俁丆侾俈乯丄乮俁丆侾俋乯丄
丂丂丂丂丂丂丂丂乮俆丆俈乯丄乮俆丆侾侾乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偺侾俈捠傝
丂傛偭偰丄媮傔傞惍悢俢偼丄丂俀亄侾俈亖侾俋乮屄乯丂偁傞丅丂丂乮廔乯
乮捛婰乯丂椷榓係擭俁寧俀侾擔晅偗
丂椷榓係擭俁寧侾俋擔乮搚乯晅偗挬擔怴暦挬姧偺乽拞妛庴尡傪怳傝曉傞乮壓乯乿偵丄椷榓係擭搙
廰扟嫵堢妛墍廰扟拞妛偺擖帋栤戣偑徯夘偝傟偰偄偨丅戝曄嫽枴怺偄栤戣偩偭偨偺偱丄彫
妛惗偵側偭偨偮傕傝偱峫偊偰傒偨丅栤戣偼庒姳夵戣偟傑偟偨丅
俁丏乮俀乯丂侾曈偺挿偝俇偺惓嶰妏宍偺柺愊偲壓恾偺嶰妏宍偺柺愊偺嵎傪媮傔傛丅
丂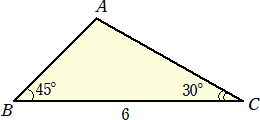
丂丂丂丂丂偨偩偟丄師偺嶲峫恾傪棙梡偟偰傕傛偄丅
丂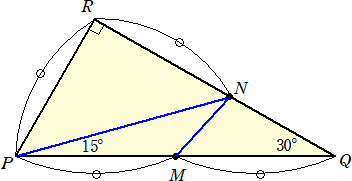
丂栤戣傪夝偔偺偑彫妛惗偩偲偄偆偙偲傪朰傟偰丄榬椡偱夝偄偰傒偨丅
丂侾曈偺挿偝俇偺惓嶰妏宍偺柺愊偼丄丂俇2 /係亖俋
/係亖俋
丂傑偨丄仮俙俛俠偺崅偝傪倛偲偍偔偲丄丂倛亄倛 亖俇丂偐傜丄丂倛亖俁乮
亖俇丂偐傜丄丂倛亖俁乮 亅侾乯丂側偺偱丄
亅侾乯丂側偺偱丄
丂仮俙俛俠亖俇丒俁乮 亅侾乯/俀亖俋乮
亅侾乯/俀亖俋乮 亅侾乯
亅侾乯
丂偟偨偑偭偰丄媮傔傞柺愊偺嵎偼丄丂俋 亅俋乮
亅俋乮 亅侾乯亖俋丂偲側傞丅
亅侾乯亖俋丂偲側傞丅
乮僐儊儞僩乯丂廰扟嫵堢妛墍廰扟拞妛偺庴尡惗偱丄忋婰偺傛偆偵夝摎偡傞彫妛惗偑偄偰傕摿
丂丂丂丂丂丂偵嬃偒偼偟側偄偩傠偆丅
丂嶲峫恾傪棙梡偟偨夝摎傪峫偊偰傒傛偆丅
乮夝乯丂俀揰俵偲俼傪寢傃丄惓嶰妏宍俹俵俼傪嶌傞丅
丂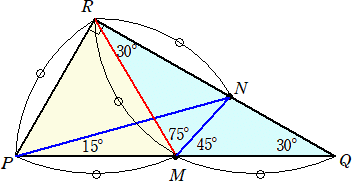
丂偙偺偲偒丄佢俶俵俻亖係俆亱偲側傝丄仮俶俵俻偑栤戣偺嶰妏宍偲側傞丅
傛偭偰丄俹俵亖俵俻亖俇偲偟偰傛偄丅偙偺偲偒丄丂仮俹俵俼亖仮俵俻俼丂側偺偱丄
丂乮侾曈偺挿偝俇偺惓嶰妏宍偺柺愊乯亅乮仮俶俵俻偺柺愊乯亖乮仮俼俵俶偺柺愊乯
偲側傞丅傛偭偰丄媮傔傞嵎偼丄丂俇亊乮俇/俀乯/俀亖俋丂偲側傞丅丂丂乮廔乯
俁丏乮俁乯丂侾曈偺挿偝俇偺惓曽宍偺拞偵丄俀偮偺惓嶰妏宍偲侾偮偺惓曽宍偑屳偄偵曈傪愙偟
丂丂丂丂丂偰擖偭偰偄傞丅
丂
丂丂偙偺偲偒丄俀偮偺惓嶰妏宍偲侾偮偺惓曽宍傪崌傢偣偨柺愊傪媮傔傛丅
乮夝乯丂壓恾偺傛偆偵丄倎丄倐 傪掕傔傞丅
丂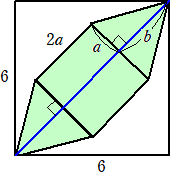
丂偙偺偲偒丄丂俀倎亄俀倐亖俇 丂傛傝丄丂倎亄倐亖俁
丂傛傝丄丂倎亄倐亖俁 丂偱偁傞丅
丂偱偁傞丅
傑偨丄倐亖 倎丂偱偁傞偺偱丄丂倎亖俁
倎丂偱偁傞偺偱丄丂倎亖俁 /乮
/乮 亄侾乯亖俁乮
亄侾乯亖俁乮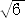 亅
亅 乯/俀
乯/俀
傛偭偰丄媮傔傞柺愊偼丄係倎2亄俀倎倐亖俀倎2亄俀倎乮倎亄倐乯亖侾俉丂丂乮廔乯
乮僐儊儞僩乯丂媮傔傞柺愊偼丄侾曈偑 倎亄倐 偺惓曽宍偺柺愊偲峫偊傜傟傞丅
丂丂
丂偙偺偲偒偼丄忋婰偺夝偲斾傋偰丄丂乮倎亄倐乯2亖侾俉丂偲娙曋偵媮傔傜傟傞丅
乮捛婰乯丂椷榓係擭俁寧俀俁擔晅偗
丂乮俁乯偑扨撈偺栤戣偱偁傟偽丄忋婰偺傛偆側夝摎偱廫暘偱偁傞偑丄偦傕偦傕栤戣宍幃偑乮侾乯
傪僸儞僩偵乮俀乯傪夝偔傛偆偵側偭偰偄傞偟丄摨條偵丄乮俀乯傪僸儞僩偵乮俁乯傪夝偔偺偑弌戣幰偺堄恾
偡傞偲偙傠偩傠偆丅
 |
丂丂媮傔傞柺愊傪愒慄偱俀暘妱偡傞丅惵慄偱弌棃傞惓嶰妏宍偐傜丄
丂偼傒弌偟偰偄傞乮偁乯偺晹暘偼丄嵍恾偺傛偆偵丄惓嶰妏宍偺拞偵
丂庢傝崬傔傞丅偙偺偲偒丄乮偄乯偺恾宍偼丄乮俀乯偱峫偊偨恾宍偱偁傞丅
丂丂傛偭偰丄惓嶰妏宍偐傜乮偄乯偺晹暘傪彍偄偨恾宍偺柺愊偼丄乮俀乯
丂偺寢壥偐傜丄俋偱偁傞丅
丂丂埲忋偐傜丄媮傔傞恾宍偺柺愊偼丄俋亊俀亖侾俉丂偲側傞丅 |
乮僐儊儞僩乯丂擄偟偄寁嶼傪偟側偔偰傕丄摫擖偵拤幚偵廬偊偽丄堈偟偄栤戣偱偟偨丅乮俀乯偑乮俁乯偺
丂丂丂丂丂丂僸儞僩偵側偭偰偄傞偙偲偵婥偯偗偽抁帪娫偱夝摎偱偒偦偆偱偡偹両
丂僇儖僺僗偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓係擭俁寧俀係擔晅偗乯
丂忋婰偺栤戣偱丄偙偺嵶挿偄榋妏宍偼丄俀偮偺捀揰偵奜愙偟偰偄傞惓曽宍偺柺愊偺敿暘偵
昁偢側傞丅
乮僐儊儞僩乯丂捀妏俁侽亱偺俀摍曈嶰妏宍乮摍曈偺挿偝亖俇乯偺俀偮暘偺柺愊偼丄侾俉偱丄惓曽宍
丂丂丂丂丂丂偺柺愊偼俁俇側偺偱丄惓曽宍偺拞偺俇妏宍偺柺愊偼丄惓曽宍偺柺愊偺敿暘偵昁
丂丂丂丂丂丂偢側傝傑偡偹両僇儖僺僗偝傫丄僫僀僗偱偡乣丅
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓係擭俁寧俀俆擔晅偗乯
丂惓曽宍偺嵍塃偵惓嶰妏宍傪偔偭偮偗偨宍偺榋妏宍偱偟傚偆偐丅偦傟側傜偽丄彫惓曽宍偺巆
傝偺2曈偵傕惓嶰妏宍傪晅偗傞偲丄巆傞寗娫偺捀妏150亱偺擇摍曈嶰妏宍偑摍愊曄宍偱丄彫
惓曽宍偺1/4偺柺愊偲傢偐傞偺偱乮榋妏宍偺拞偵偁傞(偁)偺晹暘傪丄彫惓曽宍偲嫟桳偺曈傪
屌掕偟偰捀揰傪堏摦偡傟偽彫惓曽宍偺1/4偲偨偩偪偵傢偐傝傑偡乯
丂丂丂丂
丂戝惓曽宍偼彫惓曽宍2屄+惓嶰妏宍4屄暘偲側傝丄妋偐偵丄偦偺榋妏宍偼戝惓曽宍偺敿暘
偱偡偹丅
乮捛婰乯丂椷榓係擭係寧侾俈擔晅偗
丂忋婰偺丄廰扟嫵堢妛墍廰扟拞妛偺擖帋栤戣乮俀侽俀俀乯偱丄師偺栤戣傕丄擡懴椡傪媮傔傜傟
偦偆偱嫽枴怺偄傕偺偑偁傞丅栤戣偼丄堦晹夵戣偟偰偁傝傑偡丅
侾丏(俆)丂俁寘偺悢俙俛俠丄俢俤俥丄俧俫俬 偺俁偮傪懌偡偲俀侽俀俀偵側偭偨丅俙乣 俬 偵偼侽乣俋偺侾侽
丂丂丂丂屄偺悢帤偺偆偪俋屄偺堎側傞悢帤偑侾偮偢偮擖傞丅傑偨丄俠亖俇丄俫亖侽偱偁傞丅俙乣 俬
丂丂丂丂偱巊傢側偐偭偨悢帤傪俹偲偡傞丅俙俛俠偑峫偊傜傟傞悢偺拞偱堦斣彫偝偄悢偵側傞偲偒丄
丂丂丂丂俛偲俹偼偦傟偧傟偄偔偮偐丠
乮夝乯丂侾俀俇亄俢俤俥亄俧侽俬亖俀侽俀俀丂丂俢俤俥俧俬亖俁係俆俈俉俋
丂丂丂俥亄俬亖俇丂偲側傞俥丄俬偼側偄
丂丂丂俥亄俬亖侾俇丂偺偲偒丄丂俥亖俈丄俬亖俋丂偲偟偰傒傞丅丂仺丂俤亖俉丂偱丄俢丄俧偵奩摉側偟
侾俁俇亄俢俤俥亄俧侽俬亖俀侽俀俀丂丂俢俤俥俧俬亖俀係俆俈俉俋
丂丂丂俥亄俬亖俇丂偺偲偒丄丂俥亖俀丂丄俬亖係丂偲偟偰傒傞丅丂丂仺丂俤亖俉丂偱丄俢丄俧偵奩摉側偟
丂丂丂俥亄俬亖侾俇丂偺偲偒丄丂俥亖俈丄俬亖俋丂偲偟偰傒傞丅丂仺丂俤偵奩摉偡傞悢帤偑側偄
侾係俇亄俢俤俥亄俧侽俬亖俀侽俀俀丂丂俢俤俥俧俬亖俀俁俆俈俉俋
丂丂丂俥亄俬亖俇丂偲側傞俥丄俬偼側偄
丂丂丂俥亄俬亖侾俇丂偺偲偒丄丂俥亖俈丄俬亖俋丂偲偟偰傒傞丅丂仺丂俤偵奩摉偡傞悢帤偑側偄
侾俆俇亄俢俤俥亄俧侽俬亖俀侽俀俀丂丂俢俤俥俧俬亖俀俁係俈俉俋
丂丂丂俥亄俬亖俇丂偺偲偒丄丂俥亖俀丄俬亖係丂偲偟偰傒傞丅丂仺丂俤偵奩摉偡傞悢帤偑側偄
丂丂丂俥亄俬亖侾俇丂偺偲偒丄丂俥亖俈丄俬亖俋丂偲偟偰傒傞丅丂仺丂俤偵奩摉偡傞悢帤偑側偄
侾俈俇亄俢俤俥亄俧侽俬亖俀侽俀俀丂丂俢俤俥俧俬亖俀俁係俆俉俋
丂丂丂俥亄俬亖俇丂偺偲偒丄丂俥亖俀丄俬亖係丂偲偟偰傒傞丅丂仺丂俤偵奩摉偡傞悢帤偑側偄
丂丂丂俥亄俬亖侾俇丂偲側傞俥丄俬偼側偄
侾俉俇亄俢俤俥亄俧侽俬亖俀侽俀俀丂丂俢俤俥俧俬亖俀俁係俆俈俋
丂丂丂俥亄俬亖俇丂偺偲偒丄丂俥亖俀丄俬亖係丂偲偟偰傒傞丅丂仺丂俤亖俁丂偱丄俢丄俧偵奩摉側偟
丂丂丂俥亄俬亖侾俇丂偺偲偒丄丂俥亖俈丄俬亖俋丂偲偟偰傒傞丅丂仺丂俤亖俀丂偱丄俢丄俧偵奩摉側偟
侾俋俇亄俢俤俥亄俧侽俬亖俀侽俀俀丂丂俢俤俥俧俬亖俀俁係俆俈俉
丂丂丂俥亄俬亖俇丂偺偲偒丄丂俥亖俀丄俬亖係丂偲偟偰傒傞丅丂仺丂俤偵奩摉偡傞悢帤偑側偄
丂丂丂俥亄俬亖侾俇丂偲側傞俥丄俬偼側偄
俀侾俇亄俢俤俥亄俧侽俬亖俀侽俀俀丂丂俢俤俥俧俬亖俁係俆俈俉俋
丂丂丂俥亄俬亖俇丂偲側傞俥丄俬偼側偄
丂丂丂俥亄俬亖侾俇丂偺偲偒丄丂俥亖俈丄俬亖俋丂偲偟偰傒傞丅丂仺丂俤偵奩摉偡傞悢帤偑側偄
俀俁俇亄俢俤俥亄俧侽俬亖俀侽俀俀丂丂俢俤俥俧俬亖侾係俆俈俉俋
丂丂丂俥亄俬亖俇丂偺偲偒丄丂俥亖侾丄俬亖俆丂偲偟偰傒傞丅丂仺丂俤亖俉丂偱丄俢丄俧偵奩摉側偟
丂丂丂俥亄俬亖侾俇丂偺偲偒丄丂俥亖俈丄俬亖俋丂偲偟偰傒傞丅丂仺丂俤偵奩摉偡傞悢帤偑側偄
俀係俇亄俢俤俥亄俧侽俬亖俀侽俀俀丂丂俢俤俥俧俬亖侾俁俆俈俉俋
丂丂俥亄俬亖俇丄侾俇
丂俥亄俬亖俇丂偺偲偒丄俥亖侾丄俬亖俆丂偲偟偰傒傞丅丂仺丂俤亖俈
丂丂偙偺偲偒丄丂俢亖俉丂丄俧亖俋丂偱忦審傪枮偨偡丅
丂俥亄俬亖侾俇丂偺偲偒丄俥亖俈丄俬亖俋丂偲偟偰傒傞丅丂仺丂俤偵奩摉偡傞悢帤偑側偄
丂埲忋偐傜丄丂俛亖係丂俹亖俁丂丂乮廔乯
丂Dengan kesaktian Indukmu 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓係擭係寧侾俉擔晅偗乯
丂忋婰偱丄応崌暘偗傪専摙偡傞慜偵丄俹亖俁丂偲偡偖偵傢偐傞偲巚偄傑偡丅
丂偲偄偆偺偼乧埲壓偺俀揰偵拲栚偡傞偙偲偵傛傝摫偐傟傞偲巚偄傑偡丅
嘆丂寁嶼寢壥偑俀侽俀俀偲偄偆俁偺攞悢偱偁傝側偑傜俋偺攞悢偱偼側偄揰
嘇丂偁傜偐偠傔丄俠亖俇 偲梌偊傜傟偰偄傞揰
丂俙偐傜 俬 傑偱偲俹傪崌寁偡傞偲係俆偱丄俋偺攞悢偱偡丅
丂俹亖係俆亅乮俙亄俛亄丒丒丒亄俬乯亖乮俋偺攞悢偐偮俁偺攞悢乯亅乮俋偺攞悢偱側偔丄偐偮俁偺攞悢乯
丂嘆傛傝丄俙偐傜俬傑偱傪崌寁偟偨傕偺偼丄俋偺攞悢偱偼側偔俁偺攞悢偱偡偐傜丄 俹傕傑偨俁偺
攞悢偐偮俋偺攞悢偱偼偁傝傑偣傫丅 偡側傢偪丄俹偼丄俁側偄偟俇偵峣傜傟傑偡丅
丂嘇傛傝丄俹偼俇偱偼偁傝傑偣傫丅
丂備偊偵丄俹亖俁
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓係擭係寧侾俉擔晅偗乯
丂忋婰偺栤戣丄埲壓偺傛偆偵偡傟偽帋峴嶖岆傪偩偄傇尭傜偣傑偡偐偹丠
丂椉曈傪 9 偱妱偭偨梋傝傪峫偊傞偲丄巊偭偨 9 屄偺悢帤偺崌寁傪 9 偱妱偭偨梋傝偑 6 丅
偙傟偵 P 傪壛偊傞偲丄10 屄偺悢帤偺崌寁偑 45 偵側傞傢偗偩偐傜丄P=3 偱偡丅
丂偦偟偰丄H=0 傛傝丄3亝B+E+H亝17 側偺偱丄昐偺埵傊偺孞傝忋偑傝偑 1 偱妋掕偱丄
丂A+D+G=19 偱偡丅
丂C+F+I=22 偺応崌 B+E+H=1 偲側傝晄揔側偺偱丄C+F+I=12 偱丄B+E+H=11 偲傢偐傝傑偡丅
丂C=6 偲H=0 傪峫椂偡傞偲丄A+D+G=19丄B+E=11丄F+I=6丂偱偡偑丄偙偺拞偱 1 傪巊偆偵偼丄
F+I 傪 1+5 偐 5+1 偵偡傞偟偐偁傝傑偣傫丅
丂偡傞偲丄B+E 偼丄2+9 偐 4+7 偐 7+4 偐 9+2 偲側傝丄巆傞 A+D+G 偼丄2+8+9 偐 4+7+8 偺
弴斣傪擖傟懼偊偨傕偺偲側傝傑偡丅
丂傛偭偰丄ABC 偑嵟彫偵側傞偺偼丄
丂丂ABC=246, DEF=871, GHI=905, P=3
丂丂ABC=246, DEF=875, GHI=901, P=3
丂丂ABC=246, DEF=971, GHI=805, P=3
丂丂ABC=246, DEF=975, GHI=801, P=3
偺 4 僷僞乕儞偱丄偄偢傟偺応崌傕 B=4丄P=3 偱偡丅
丂Dengan kesaktian Indukmu 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓係擭係寧侾俉擔晅偗乯
丂DD++偝傫偺夝愢偵彑傞傾僞僢僋儖乕僩偼側偄偲懚偠傑偡丅
乮僐儊儞僩乯丂夝摎偑偩偄傇僗僢僉儕偱偒偦偆偱偡両Dengan kesaktian Indukmu 偝傫丄DD++ 偝傫
丂丂丂丂丂丂偵姶幱偟傑偡丅
丂俀侽俀俀傪俋偱妱偭偨梋傝偑俇偵婥偑偮偔偲丄俹亖俁偑堦弖偱暘偐傞傫偱偡偹丅姶摦偟傑偟偨丅
丂偙傟偱巊偊傞悢帤丂侾俀係俆俈俉俋丂偑妋掕偟偨偺偑戝偒偄偱偡偹丅
丂昐偺埵偱偺孞傝忋偑傝傪峫偊傞偲丄俥亄俬亖侾俇偼婲偙傝偊偢丄俥亄俬亖俇側偺偱丄俥亖侾丄俬亖俆偲
弌棃傑偡丅乮懠偺応崌傕偁傝摼傞偑丄偦傟偼峫偊傞堄枴偑側偄乯
丂俛亄俤亖侾侾偱丄昐偺孞傝忋偑傝偲俙俛俠偑嵟彫偲偄偆偙偲傪峫偊傞偲丄俛亖係丄俤亖俈丂偱偡丅
丂屻偼巊偊傞悢帤丂俀俉俋丂偲俙俛俠偑嵟彫偲偄偆偙偲傪峫偊偰丄丂俙亖俀丄俢亖俉丄俧亖俋丂偲弌棃
傑偡丅
丂埲忋偐傜丄丂俛亖係丂俹亖俁丂偱偁傞偙偲偑暘偐傞丅
丂俧俙俬 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓係擭係寧侾俋擔晅偗乯
丂偍偠偝傫偼慡専嶕偱弌偡偟偐側偔丄
246;871;905丂丂246;875;901丂丂246;971;805丂丂246;975;801
276;841;905丂丂276;845;901丂丂276;941;805丂丂276;945;801
426;791;805丂丂426;795;801丂丂426;891;705丂丂426;895;701
496;721;805丂丂496;725;801丂丂496;821;705丂丂496;825;701
726;491;805丂丂726;495;801丂丂726;891;405丂丂726;895;401
796;421;805丂丂796;425;801丂丂796;821;405丂丂796;825;401
826;491;705丂丂826;495;701丂丂826;791;405丂丂826;795;401
846;271;905丂丂846;275;901丂丂846;971;205丂丂846;975;201
876;241;905丂丂876;245;901丂丂876;941;205丂丂876;945;201
896;421;705丂丂896;425;701丂丂896;721;405丂丂896;725;401
946;271;805丂丂946;275;801丂丂946;871;205丂丂946;875;201
976;241;805丂丂976;245;801丂丂976;841;205丂丂976;845;201
偺慡晹偱48僷僞乕儞偑偁傝丄ABC偺嵟彫偲側傞偺偑巒傔偺4屄偱偡傛偹丅
丂偙傟傪彫妛俇擭惗偑夝偔偺偐両悢妛偺椡偼擭楊偵偼慡偔娭學偟側偄偙偲傪夵傔偰姶偠擖偭
偨偙偲偱偟偨丅
乮捛婰乯丂椷榓俇擭俇寧俀俇擔晅偗
丂埲慜丄奐惉拞妛偺擖帋栤戣乮俀侽俀俀乯傪専摙偟偰丄偦偺傑傑曻抲偝傟偰偄傞傕偺偑偁偭偨丅
抶傟偽偣側偑傜捛婰偟偰偍偒傑偡丅栤戣偼丄堦晹夵戣偟偰偁傝傑偡丅
侾丏乮俁乯丂係偮偺偝偄偙傠傪搳偘傞丅栚偺愊偑係偺攞悢偲側傞栚偺弌曽偼壗捠傝偐丅
乮夝乯丂倎倐們倓丂彮側偔偲傕侾屄偑係側傜偽丄栚偺愊偼係偺攞悢側偺偱丄丂丂俇4亅俆4亖俇俈侾
丂俀偺攞悢偑俀屄埲忋側傜偽丄栚偺愊偼係偺攞悢偲側傞丅
丂丂係偑侽枃偱丂俀or俇偑俀枃丂仺丂4俠2亊俀2亊俁2亖俀侾俇
丂丂係偑侽枃偱丂俀or俇偑俁枃丂仺丂4俠3亊俀3亊俁亖俋俇
丂丂係偑侽枃偱丂俀or俇偑係枃丂仺丂4俠4亊俀4亖侾俇
丂埲忋偐傜丄丂俇俈侾亄俀侾俇亄俋俇亄侾俇亖俋俋俋乮捠傝乯丂丂乮廔乯
丂俧俙俬 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭俇寧俀俉擔晅偗乯
丂摢傪偳偆惍棟偡傟偽偄偄偺偐丠忋婰偺乽係偮偺偝偄偙傠傪搳偘傞丅栚偺愊偑係偺攞悢偲側傞
栚偺弌曽偼壗捠傝偐丅乿傪彫妛惗偑挧愴偡傞栤戣偵姶怱偟側偑傜夝摎傪撉傫偱丄摨偠愝掕偱丄
偱偼丄栚偺愊偑俇偺攞悢偲側傞栚偺弌曽偼壗捠傝偁傞偺偐偲丄夝摎偺傗傝曽傪嶲峫偵偟側偑
傜偁傟偙傟帺暘側傝偺幃傪漵偹忋偘偰寁嶼偝偣偰傒偨傜丄惓夝偲偢傟偰偄傞偱偼側偄偐丅
惓夝偲巚傢傟傞悢偼僾儘僌儔儉偵棅偭偰弌偟偨傕偺偵側傝傑偡丅
丂偙傫側偺傪彫妛惗偑挧愴偱偒傞偲偄偆堘偄偑傑偢嬃偒偱偡丅壗曽偐嵟傕岠棪傛偄庤寁嶼偵
傛傞媮傔曽傪偛嫵庼壓偝偄丅
丂Dengan kesaktian Indukmu 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭俇寧俀俉擔晅偗乯
丂梋帠徾偑壗捠傝側偺偐偵偮偄偰曪彍尨棟傪巊偭偰 321 捠傝丅
幚嵺偵丄偡傋偰婏悢丗3^4 = 81
丂偡傋偰俁偺攞悢偱側偄丗4^4 = 256
丂椉曽偺忦審傪枮偨偡乮1偲5偺傒乯丗2^4 = 16
丂曪彍尨棟偵傛傝丄梋帠徾乮6偺攞悢偵側傜側偄帠徾)偺応崌偺悢偼 321 捠傝丅
丂慡帠徾偑 1296 捠傝側偺偱丄媮傔傞帠徾(俇偺攞悢偵側傞)偺応崌偺悢偼丄975捠傝
乧乧偲寁嶼偟偰傒傑偟偨丅
丂係偺攞悢僶乕僕儑儞偱偺夝摎偲偼暿偺曽朄偱丅傕偟傕巹偑彫妛惗偵嫵偊傞側傜偙偆偟傑偡丅
丂梋帠徾傪峫偊傞偲丄慡晹婏悢偐丄俁屄偑婏悢偱巆傝偑2傑偨偼6偺栚偱丅
丂6*6*6*6-(3*3*3*3+2*3*3*3+3*2*3*3+3*3*2*3+3*3*3*2) = 999
仈寢嬊偺偲偙傠丄梋帠徾傪寁嶼偡傞傎偆偑憗偄働乕僗傕偁傞乧偲嫵偊傞偲巚偆偺偱偡傛偹丅
丂傝傜傂偄偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭俇寧俀俉擔晅偗乯
丂忋婰偺乮夝乯偺曽朄傪嶲峫偵偡傞側傜丄師偺傛偆側姶偠偱偟傚偆偐丅
仢係偮偺偝偄偙傠傪搳偘傞丅栚偺愊偑俇偺攞悢偲側傞栚偺弌曽偼壗捠傝偐丅
丂彮側偔偲傕1屄偑"6"側傜偽丄栚偺愊偼6偺攞悢側偺偱丄6^4-5^4=671捠傝
"3"偑1屄埲忋偐偮("2"傑偨偼"4")偑1屄埲忋側傜偽丄栚偺愊偼6偺攞悢偲側傞丅
"6"偑側偔丄"3"偑1屄丄("2"傑偨偼"4")偑1屄 乧 4!/(1!1!2!)*1*2*2^2=96捠傝
"6"偑側偔丄"3"偑1屄丄("2"傑偨偼"4")偑2屄 乧 4!/(1!2!1!)*1*2^2*2=96捠傝
"6"偑側偔丄"3"偑1屄丄("2"傑偨偼"4")偑3屄 乧 4!/(1!3!)*1*2^3=32捠傝
"6"偑側偔丄"3"偑2屄丄("2"傑偨偼"4")偑1屄 乧 4!/(2!1!1!)*1^2*2*2=48捠傝
"6"偑側偔丄"3"偑2屄丄("2"傑偨偼"4")偑2屄 乧 4!/(2!2!)*1^2*2^2=24捠傝
"6"偑側偔丄"3"偑3屄丄("2"傑偨偼"4")偑1屄 乧 4!/(3!1!)*1^3*2=8捠傝
丂埲忋偐傜丄671+96+96+32+48+24+8=975捠傝
丂恀傫拞偺寁嶼検傪傕偆彮偟尭傜偡偲師偺傛偆偵側傝傑偡丅
仢係偮偺偝偄偙傠傪搳偘傞丅栚偺愊偑俇偺攞悢偲側傞栚偺弌曽偼壗捠傝偐丅
丂彮側偔偲傕1屄偑"6"側傜偽丄栚偺愊偼6偺攞悢側偺偱丄6^4-5^4=671捠傝
丂"3"偑1屄埲忋偐偮("2"傑偨偼"4")偑1屄埲忋側傜偽丄栚偺愊偼6偺攞悢偲側傞丅
偙傟偼丄"6"偑1屄傕娷傑傟側偄応崌偺偆偪丄
4屄偲傕"3"偱側偄応崌偲4屄偲傕("2"傑偨偼"4")偱側偄応崌傪彍奜偟丄廳暋偟偰彍奜偟偰偄傞
4屄偲傕("1"傑偨偼"5")偱偁傞応崌傪懌偟側偍偣偽傛偄偺偱丄丂5^4-4^4-3^4+2^4=304捠傝
丂埲忋偐傜丄671+304=975捠傝
丂偟偐偟丄師偺曽朄偺曽偑傢偐傝傗偡偄偲巚偄傑偡丅
仢係偮偺偝偄偙傠傪搳偘傞丅栚偺愊偑俇偺攞悢偲側傞栚偺弌曽偼壗捠傝偐丅
丂栚偺愊偑俇偺攞悢偲側傜側偄栚偺弌曽傪峫偊傞丅
丂乽4偮偲傕婏悢偺応崌偺悢嘆乿偲乽4偮偲傕3偺攞悢偱側偄応崌偺悢嘇乿偺榓偐傜
乽4偮偲傕婏悢偱傕3偺攞悢偱傕側偄応崌偺悢嘊乿傪堷偗偽傛偄丅
嘆丂4偮偲傕婏悢偱偁傞偲偒 乧 3^4=81捠傝
嘇丂4偮偲傕3偺攞悢偱側偄偲偒 乧 4^4=256捠傝
嘊丂4偮偲傕"1"傑偨偼"5"偵側傞偲偒 乧 2^4=16捠傝
傛偭偰丄栚偺愊偑俇偺攞悢偲側傜側偄栚偺弌曽偼丄81+256-16=321捠傝
丂偡傋偰偺栚偺弌曽偼 6^4=1296捠傝 側偺偱丄栚偺愊偑俇偺攞悢偲側傞栚偺弌曽偼丄
1296-321=975捠傝
仈傕偲偺栤戣傕丄偙偪傜偺曽偑傢偐傝傗偡偄偐傕偟傟傑偣傫丅
仢係偮偺偝偄偙傠傪搳偘傞丅栚偺愊偑係偺攞悢偲側傞栚偺弌曽偼壗捠傝偐丅
丂栚偺愊偑係偺攞悢偲側傜側偄栚偺弌曽傪峫偊傞丅
嘆丂4偮偲傕婏悢偵側傞偲偒 乧 3^4=81捠傝
嘇丂3偮偑婏悢偱巆傝1偮偑"2"傑偨偼"6"偺偲偒 乧 (4C1)*3^3*2=216捠傝
丂偡傋偰偺栚偺弌曽偼 6^4=1296捠傝 側偺偱丄栚偺愊偑係偺攞悢偲側傞栚偺弌曽偼丄
1296-81-216=999捠傝
丏丏丏偲丄偙偙傑偱彂偄偨屻偱丄GAI偝傫偺栤偄偐偗偑丄
丂壗曽偐嵟傕岠棪傛偄庤寁嶼偵傛傞媮傔曽傪偛嫵庼壓偝偄丅
偲偄偆傕偺偱偁傞偙偲偵婥偯偄偨丅岠棪偺埆偄夝摎傪彂偄偰偟傑偭偨傛乧乧丅偱傕丄偣偭偐偔
彂偄偨偺偱慡晹搳峞偟偰偍偒傑偡丅
丂俧俙俬 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭俇寧俀俉擔晅偗乯
丂Dengan kesaktian Indukmu 偝傫偺
丂偡傋偰婏悢丗3^4 = 81
丂偡傋偰俁偺攞悢偱側偄丗4^4 = 256
丂椉曽偺忦審傪枮偨偡乮1偲5偺傒乯丗2^4 = 16
丂曪彍尨棟偵傛傝丄梋帠徾乮6偺攞悢偵側傜側偄帠徾)偺応崌偺悢偼 321 捠傝丅
丂傝傜傂偄偝傫偺
丂栚偺愊偑俇偺攞悢偲側傜側偄栚偺弌曽傪峫偊傞丅
丂乽4偮偲傕婏悢偺応崌偺悢嘆乿偲乽4偮偲傕3偺攞悢偱側偄応崌偺悢嘇乿偺榓偐傜
乽4偮偲傕婏悢偱傕3偺攞悢偱傕側偄応崌偺悢嘊乿傪堷偗偽傛偄丅
嘆丂4偮偲傕婏悢偱偁傞偲偒 乧 3^4=81捠傝
嘇丂4偮偲傕3偺攞悢偱側偄偲偒 乧 4^4=256捠傝
嘊丂4偮偲傕"1"傑偨偼"5"偵側傞偲偒 乧 2^4=16捠傝
傛偭偰丄栚偺愊偑俇偺攞悢偲側傜側偄栚偺弌曽偼丄81+256-16=321捠傝
丂偍擇恖偲傕傛偔偙偺岠棪椙偄傾僀僨傾偵偨偳傝偮偗傑偡偹乣丅嵟弶傝傜傂偄偝傫偺條偵捈愙
媮傔傛偆偲偟偰丄応崌偑寢峔戲嶳偵暘偐傟偰峴偭偰偟傑偄丄摢偺拞偑偛偪傖偛偪傖偲崿棎偟偰
峴偒傑偟偨丅偟偐偟丄梋帠徾偵偁偨傞俇偺攞悢偵側傟側偄僷僞乕儞悢傪嶌傝弌偡寁嶼幃偑丄偙
傫側偵傕僗僢僉儕偲捇傞側傫偰巚偭偰傕偄傑偣傫偱偟偨丅
丂傒側偝傫偺僙儞僗傪尒廗偭偰惛恑惛恑丅
乮捛婰乯丂椷榓俇擭俇寧俀俋擔晅偗
丂崱偐傜侾係擭慜偺乽暯惉俀俀擭俆寧俆擔晅偗乿偱丄俧俙俬 偝傫偺採婲偝傟偨栤戣傪偒偭偐偗偲偟
偰丄乽栚偺愊乿偺儁乕僕偑婲偙偝傟偨丅
丂偦偺拞偱丄奐惉拞妛乮俼侽係乯偺栤戣偼丄暯惉係擭偺嫗搒戝妛偺擖帋栤戣偑弌揟偩傠偆偲悇
嶡偝傟傞丅梋帠徾偱峫嶡偡傞偺偑億僀儞僩偲僐儊儞僩偝傟偰偄傞丅
嫗搒戝妛丂慜婜乮侾俋俋俀乯丂乮侾乯乮俀乯丗暥宯丂乮侾乯乮俁乯丗棟宯
丂偝偄偙傠傪孞傝曉偟 値 夞怳偭偰丄弌偨栚偺悢傪妡偗崌傢偣偨愊傪倃偲偡傞丅偡側傢偪丄
倠 夞栚偵弌偨栚偺悢傪 倄倠 偲偡傞偲丄丂倃亖倄1倄2丒丒丒倄n
丂(侾)丂倃偑俁偱妱傝愗傟傞妋棪 倫値 傪媮傔傛丅
丂(俀)丂倃偑係偱妱傝愗傟傞妋棪 倯値 傪媮傔傛丅
丂(俁)丂倃偑俇偱妱傝愗傟傞妋棪 倰値 傪媮傔傛丅
丂偦偙偱偼丄傐偭傐偝傫傗丄俥俶偝傫丄倎倲 偝傫側偳偑峫嶡傪廳偹偰偄傞丅
丂乮俀乯偺寢壥偼丄倫値亖侾亅乮俀値亄俁乯(侾/俀)値/俁丂偱偁傞偑丄偙傟傪傕偲偵丄値亖係偺偲偒偵栚偺
愊偑係偺攞悢偵側傞応崌偺悢傪媮傔傟偽丄
丂乮侾亅侾侾/係俉乯亊俇4亖俋俋俋丂偲側傝丄摎偊偑堦抳偡傞丅
丂摨條偵丄値亖係偺偲偒偵栚偺愊偑俇偺攞悢偵側傞応崌偺悢傪媮傔傟偽丄
丂乮俁乯偺寢壥丄倫値亖侾亅(俀/俁)値亅(侾/俀)値亄(侾/俁)値丂傪梡偄偰丄
丂乮侾亅侾俇/俉侾亅侾/侾俇亄侾/俉侾乯亊俇4亖俋俈俆丂偲側傝丄摎偊偑堦抳偡傞丅
乮捛婰乯丂椷榓俆擭俀寧俇擔晅偗
丂椷榓俆擭俀寧俆擔乮擔乯晅偗挬擔怴暦挬姧偵椷榓俆擭搙嶗堻拞妛擖帋栤戣偑宖嵹偝傟偨丅
偄偔偮偐柺敀偦偆側栤戣偑偁偭偨偺偱丄彫妛惗偵側偭偨偮傕傝偱峫偊偰傒偨丅
侾丏乮俀乯丂係偮偺帟幵俙丄俛丄俠丄俢偑偁傝丄俙偲俛丄俠偲俢偼偦傟偧傟偐傒崌偭偰偄傞丅俛偲俠偼
丂丂丂丂丂摨偠幉偵庢傝晅偗傜傟偰偍傝丄妸傞偙偲側偔堦弿偵夞傞丅
丂丂丂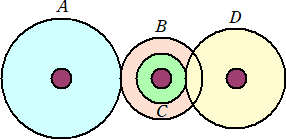
丂俙丄俛丄俠偺帟悢偼丄偦傟偧傟俇俉丄係俉丄俀俈偱丄俙偑侾侾夞揮偡傞偲偒丄俢偼丄侾俉俈/俀係夞揮
偡傞丅偙偺偲偒丄師偺栤偄偵摎偊傛丅
乮僀乯丂俢偺帟悢傪媮傔傛丅
乮儘乯丂俙偑俆夞揮偡傞偺偵俁昩偐偐傞偲偡傞偲丄俢偼侾俀夞揮偡傞偺偵壗昩偐偐傞偐丅
乮夝乯乮僀乯丂俛偺夞揮悢傪倐丄俢偺帟悢傪俢偲偍偔偲丄
丂俇俉亊侾侾亖係俉亊倐丂傛傝丄丂倐亖侾俉俈/侾俀丂偲側傞丅
丂偙偺偲偒丄俠偺夞揮悢傕侾俉俈/侾俀側偺偱丄丂乮侾俉俈/侾俀乯亊俀俈亖乮侾俉俈/俀係乯亊俢丂傛傝丄
丂俢亖俀俈亊俀亖俆係丂偲側傞丅
乮儘乯丂俙偑俆夞揮偡傞偲偒丄俢偼丄乮侾俉俈/俀係乯亊乮俆/侾侾乯亖俉俆/俀係乮夞揮乯偟丄俁昩偐偐傞丅
丂傛偭偰丄俢偑侾俀夞揮偡傞偲偒丄丂侾俀亐乮俉俆/俀係乯亊俁亖俉俇係/俉俆乮昩乯丂偐偐傞丅丂丂乮廔乯
乮暿夝乯乮僀乯丂帟悢偲夞揮悢偼斀斾椺偡傞偺偱丄俛偺夞揮悢偼丄侾侾亊乮俇俉/係俉乯亖侾俉俈/侾俀
丂偙偺偲偒丄俠偺夞揮悢傕丄侾俉俈/侾俀偲側傞偺偱丄俢偺帟悢傪俢偲偍偔偲丄
丂俀俈 丗 俢亖侾俉俈/俀係 丗 侾俉俈/侾俀亖侾 丗 俀丂傛傝丄丂俢亖俀俈亊俀亖俆係丂偲側傞丅丂丂乮廔乯
嘦丂廲俁侽侽倣丄墶俆侽侽倣偺挿曽宍偺搚抧偑偁傝丄偦偺傑傢傝偵壓恾偺傛偆偵侾侽倣偍偒偵婙
丂傪棫偰傞寠偑嬻偄偰偄傞丅挿曽宍偺巐嬿偵偼寠偼嬻偄偰偄側偄傕偺偲偡傞丅
丂丂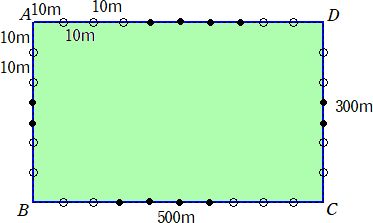
丂偙偺偲偒丄師偺栤偄偵摎偊傛丅
乮侾乯丂慡偰偺寠偵婙傪棫偰傞偲偒丄婙偼慡晹偱壗杮昁梫偐丅
乮俀乯丂壴巕偝傫偑挿曽宍偺搚抧偺抧揰俙偐傜帪寁夞傝偵恑傫偱婙傪棫偰傞丅曕偔懍偝偼暘懍
丂丂俈侽倣偱丄侾杮偺婙傪棫偰傞偺偵梫偡傞帪娫偼丄俈/俁暘偲偡傞丅
丂丂壴巕偝傫偑抧揰俙傪弌敪偟偰嵟屻偺寠偵婙傪棫偰廔偊傞傑偱偵梫偡傞帪娫傪媮傔傛丅
乮俁乯丂壴巕偝傫偲嶗偝傫偼抧揰俙傪摨帪偵弌敪偟丄俀恖偲傕摨偠懍偝偱丄壴巕偝傫偼帪寁夞傝丄
丂丂嶗偝傫偼斀帪寁夞傝偵婙傪棫偰偰偄偔丅偨偩偟丄嶗偝傫偑婙傪侾杮棫偰傞偺偵梫偡傞帪娫
丂丂偼丄俀暘偲偡傞丅
丂丂壴巕偝傫偑抧揰俢偵拝偔傑偱偺帪娫丄嶗偝傫偑抧揰俠偵拝偔傑偱偺帪娫傪偦傟偧傟媮傔傛丅
乮係乯丂俀恖偑抧揰俙傪弌敪偟偰嵟屻偺婙傪棫偰傞傑偱偵梫偡傞帪娫傪媮傔傛丅偨偩偟丄愭偵寠
丂丂偵拝偄偨恖偑婙傪棫偰傞傕偺偲偡傞丅
乮夝乯乮侾乯丂俆侽侽亐侾侽亅侾亖係俋丂丄俁侽侽亐侾侽亅侾亖俀俋丂傛傝丄丂乮係俋亄俀俋乯亊俀亖侾俆俇乮杮乯
乮俀乯丂侾侽倣偛偲偵侾杮婙傪棫偰傞偺偵梫偡傞帪娫偼丄丂侾/俈亄俈/俁亖俆俀/俀侾丂側偺偱丄
丂丂乮俆俀/俀侾乯亊侾俆俇亄俁亊乮侾/俈乯亖俀俈侽俈/俈乮暘乯
丂丂丂丒丒丒丂帪娫偵捈偟偰丄丂俇帪娫乮俀俇亄俆/俈乯暘
乮俁乯丂壴巕偝傫偑抧揰俢偵拝偔傑偱偺帪娫 丗 乮俆俀/俀侾乯亊係俋亄侾/俈亖俀俆俆侾/俀侾
丂丂丂丒丒丒丂帪娫偵捈偟偰丄丂俀帪娫乮侾亄侾侽/俀侾乯暘
丂嶗偝傫偑丄侾侽倣偛偲偵侾杮婙傪棫偰傞偺偵梫偡傞帪娫偼丄丂侾/俈亄俀亖侾俆/俈丂側偺偱丄
丂嶗偝傫偑抧揰俠偵拝偔傑偱偺帪娫 丗 乮侾俆/俈乯亊乮俀俋亄係俋乯亄俀亊乮侾/俈乯亖侾侾俈俀/俈
丂丂丂丒丒丒丂帪娫偵捈偟偰丄丂俀帪娫乮係俈亄俁/俈乯暘
乮係乯丂壴巕偝傫丄嶗偝傫偑抧揰俙傪弌敪偟偰丄嶗偝傫偑抧揰俠偵拝偄偨偲偒丄壴巕偝傫偼丄慄
丂丂暘俠俢忋偵偄傞丅
丂慄暘俠俢忋偺寠偵丄抧揰俢懁傛傝抧揰俠偵岦偐偭偰弴斣偵斣崋侾丄俀丄俁丄丒丒丒丄俀俋傪晅偗傞丅
丂侾侾俈俀/俈亅俀俆俆侾/俀侾亖俋俇俆/俀侾丂偱丄俋俇俆/俀侾亐俆俀/俀侾亖侾俉亄俀俋/俆俀丂傛傝丄
壴巕偝傫偼丄寠斣崋侾俉偵婙傪棫偰丄師偺寠斣崋侾俋偵岦偐偭偰偄傞偲偙傠偱偁傞丅
丂寠斣崋侾俋傑偱偼丄偁偲丂俋俇俆/俀侾亅侾俉亊乮俆俀/俀侾乯亖俀俋/俀侾乮暘乯偐偐傞丅
丂嶗偝傫偑抧揰俠傪弌敪偟偰偐傜帪娫傪寁傝巒傔偰丄
丂壴巕偝傫偑寠斣崋侾俋偵拝偔傑偱丂丒丒丒丂俀俋/俀侾乮暘乯
丂嶗偝傫偑寠斣崋俀俋偵拝偔傑偱丂丒丒丒丂侾俆/俈乮暘乯
丂壴巕偝傫偑寠斣崋俀侽偵拝偔傑偱丂丒丒丒丂乮俀俋/俀侾乯亄乮俆俀/俀侾乯亖俉侾/俀侾乮暘乯
丂嶗偝傫偑寠斣崋俀俉偵拝偔傑偱丂丒丒丒丂乮侾俆/俈乯亊俀亖俁侽/俈乮暘乯
丂壴巕偝傫偑寠斣崋俀侾偵拝偔傑偱丂丒丒丒丂乮俀俋/俀侾乯亄乮俆俀/俀侾乯亊俀亖侾俁俁/俀侾乮暘乯
丂嶗偝傫偑寠斣崋俀俈偵拝偔傑偱丂丒丒丒丂乮侾俆/俈乯亊俁亖係俆/俈乮暘乯
丂壴巕偝傫偑寠斣崋俀俀偵拝偔傑偱丂丒丒丒丂乮俀俋/俀侾乯亄乮俆俀/俀侾乯亊俁亖侾俉俆/俀侾乮暘乯
丂嶗偝傫偑寠斣崋俀俇偵拝偔傑偱丂丒丒丒丂乮侾俆/俈乯亊係亖俇侽/俈乮暘乯
丂壴巕偝傫偑寠斣崋俀俁偵拝偔傑偱丂丒丒丒丂乮俀俋/俀侾乯亄乮俆俀/俀侾乯亊係亖俀俁俈/俀侾乮暘乯
丂嶗偝傫偑寠斣崋俀俆偵拝偔傑偱丂丒丒丒丂乮侾俆/俈乯亊俆亖俈俆/俈乮暘乯
丂壴巕偝傫偑寠斣崋俀係偵拝偔傑偱丂丒丒丒丂乮俀俋/俀侾乯亄乮俆俀/俀侾乯亊俆亖俀俉俋/俀侾乮暘乯
丂嶗偝傫偑寠斣崋俀係偵拝偔傑偱丂丒丒丒丂乮侾俆/俈乯亊俇亖俋侽/俈亖俀俈侽/俀侾乮暘乯
丂傛偭偰丄嶗偝傫偺曽偑壴巕偝傫傛傝愭偵寠斣崋俀係偵拝偄偰丄婙傪棫偰傞丅
丂埲忋偐傜丄嵟屻偺婙傪棫偰傞傑偱偵梫偡傞帪娫偼丄
丂丂侾侾俈俀/俈亄俋侽/俈亖侾俀俇俀/俈
丂丂丂丒丒丒丂帪娫偵捈偟偰丄丂俁帪娫俀/俈暘丂丂乮廔乯
乮僐儊儞僩乯丂怱偑愜傟偦偆側斚嶨側寁嶼偱偁傞偑丄峫偊曽偼扨弮側偺偱丄崻婥偑偁傞偐偳偆偐
丂丂丂丂丂丂帋偝傟偰偄傞傛偆側婥暘丏丏丏丅
嘨丂俙丄俛偺俀恖偑偦傟偧傟侾偮偢偮偺偝偄偙傠傪摨帪偵傆偭偰丄弌偨栚偵傛偭偰彑攕傪寛傔
丂摼揰傪偮偗傞僎乕儉傪偡傞丅
乮儖乕儖乯
彑攕偵偮偄偰
丒偝偄偙傠偺栚偼丄丂乽侾乿亜乽慺悢乿亜乽侾偱傕慺悢偱傕側偄悢乿丂偺弴偵嫮偄偲偟丄嫮偄栚傪弌偟
丂偨曽偑彑偪偲偡傞丅偨偩偟丄乽俇乿偼乽侾乿偵彑偮偲偡傞丅
丒俀偮偲傕摨偠栚偺悢偺偲偒偼丄偁偄偙偲偡傞丅
丒偁偄偙偱側偔丄俀偮偲傕乽慺悢乿偐丄俀偮偲傕乽侾偱傕慺悢偱傕側偄悢乿偺偲偒偼丄戝偒偄悢偺曽傪
丂彑偪偲偡傞丅
摼揰偵偮偄偰
丒偼偠傔偼俀恖偲傕侽揰偲偡傞丅
丒侾夞傆偭偰彑攕偑寛傑偭偨偲偒偼丄彑偭偨曽偑侾揰丄晧偗偨曽偑侽揰偲偡傞丅偁偄偙偺偲偒偼
丂揰偼側偄丅
丒偁偄偙偩偭偨師偵彑攕偑寛傑偭偨偲偒偼丄偁偄偙偩偭偨摨偠栚偺悢傪彑偭偨曽偺揰偲偡傞丅
丂偁偄偙偑懕偄偨偲偒傕丄偦偺師偵彑攕偑寛傑偭偨傜丄偁偄偙偵側偭偨摨偠栚偺悢傪懌偟偰
丂彑偭偨曽偺揰偲偡傞丅偳偪傜偺偲偒傕丄晧偗偨曽偼侽揰偲偡傞丅
丂偙偺偲偒丄師偺栤偄偵摎偊傛丅
乮侾乯丂俀夞傆偭偰俙偑俁揰傪摼傞偲偒丄俙偲俛偺栚偺弌曽偼壗捠傝偁傞偐丅
乮俀乯嘆丂俁夞傆偭偰俙偲俛偑摨揰偵側偭偨偲偒丄俙偺摼揰偲偟偰峫偊傜傟傞悢傪偡傋偰媮傔傛丅
丂嘇丂嘆偺偲偒偺俙偲俛偺栚偺弌曽偺慻偼慡晹偱壗捠傝偁傞偐丅
乮夝乯乮侾乯丂俀夞傆偭偰俙偑俁揰傪摼傞偨傔偵偼丄侾夞栚偑偁偄偙乮栚偼俁乯偱丄俀夞栚俙偺彑偪
丂丂丂丂丂偺偲偒偱偁傞丅
丂戣堄傛傝丄侾偑彑偮悢偼丄俀丄俁丄係丄俆丂丂俀偑彑偮悢偼丄係丄俇丂丂俁偑彑偮悢偼丄俀丄係丄俇
丂丂丂丂丂丂丂俆偑彑偮悢偼丄俀丄俁丄係丄俇丂丂俇偑彑偮悢偼丄侾丄係
丂傛偭偰丄俙丄俛偺栚偺弌曽偼丄慡晹偱丄侾俆捠傝丂偁傞丅
乮俀乯嘆丂偁偄偙偺夞悢偱応崌暘偗偡傞丅
丂偁偄偙偺夞悢侽夞偍傛傃俀夞偺偲偒丄俙丄俛偑摨揰偵側傞偙偲偼側偄偐傜丄婲偙傝偊側偄丅
丂偁偄偙偺夞悢侾夞偺偲偒丄
丂丂偁偄偙侾夞栚偵弌傞偲偒丄俙丄俛偑摨揰偵側傞偨傔偵偼丄俙丄俛偺侾彑侾攕偱丄偁偄偙偺栚偼侾
丂丂偁偄偙俀夞栚偵弌傞偲偒丄俙丄俛偑摨揰偵側傞偨傔偵偼丄俙丄俛偺侾彑侾攕偱丄偁偄偙偺栚偼侾
丂丂偁偄偙俁夞栚偵弌傞偲偒丄俙丄俛偑摨揰偵側傞偨傔偵偼丄俙丄俛偺侾彑侾攕偱丄偁偄偙偺栚偼
丂壗偱傕傛偄丅
丂偁偄偙偺夞悢俁夞偺偲偒丄俙丄俛偺摼揰偼偲傕偵侽揰偵側傞丅
丂埲忋偐傜丄俙偺摼揰偲偟偰峫偊傜傟傞悢偼丄丂侽丂傑偨偼丂侾丂偱偁傞丅
嘇丂嘆偺応崌暘偗偵拲堄偟偰丄媮傔傞応崌偺悢偼丄
丂侾俆亊侾俆亊係亄侾俆亊侾俆亊俀亊俇亄俇亊俇亊俇亖俁俉侾俇乮捠傝乯
乮僐儊儞僩乯丂儖乕儖偑暋嶨偱丄撉傒崬傒偑戝曄偱偡偹丅乽侾乿偼僆乕儖儅僀僥傿乕偩偗偳乽俇乿偵
丂丂丂丂丂丂晧偗傞偲偄偆儖乕儖偼丄僩儔儞僾僎乕儉偺僫億儗僆儞偵帡偰偄傑偡偹丅
嘩丂侾曈偑侾侽們倣偺棫曽懱偑偁傞丅忋柺偺拞怱偵偼敿宎侾偺墌俙偑偁傝丄忋柺偵悅捈偵丄
丂丂昩懍侾們倣偱懳柺傑偱摦偔丅偙偺偲偒丄墌俙偑捠夁偟偨晹暘傪棫曽懱偐傜偔傝敳偄偰弌棃傞
丂丂棫懱傪峫偊傞丅師偺栤偄偵摎偊傛丅
乮侾乯丂墌俙偑摦偒巒傔偰偐傜俈昩屻偺棫懱偺懱愊傪媮傔傛丅
丂偝傜偵丄庤慜偺柺偵偼丄廲係們倣丄墶俀們倣偺挿曽宍俛偑偁傝丄壓恾偺傛偆偵側偭偰偄傞丅
丂丂丂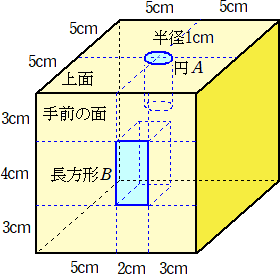
丂挿曽宍俛偼墌俙偲摨帪偵弌敪偟丄庤慜偺柺偵悅捈偵懳柺傑偱摦偔丅墌俙偑捠夁偟偨晹暘偵
壛偊偰丄挿曽宍俛偑捠夁偟偨晹暘傕棫曽懱偐傜偔傝敳偄偰弌棃傞棫懱傪峫偊傞丅偨偩偟丄墌俙
偲挿曽宍偼偍偨偑偄偵傇偮偐偭偰傕巭傑傞偙偲側偔摦偒懕偗傞傕偺偲偡傞丅
乮俀乯丂挿曽宍俛偺摦偔懍偝偼丄昩懍俀們倣偲偡傞丅墌俙偲挿曽宍俛偑摦偒巒傔偰偐傜俁昩屻偲
丂丂俆昩屻偺棫懱偺懱愊傪媮傔傛丅
乮俁乯丂挿曽宍俛偺摦偔懍偝偼丄昩懍侽丏俇俀俆們倣偲偡傞丅墌俙偲挿曽宍俛偑摦偒巒傔偰偐傜俉昩
丂丂屻偺棫懱偺懱愊傪媮傔傛丅
乮係乯丂墌俙偲挿曽宍俛偑摦偒巒傔偰偐傜俋昩屻偺棫懱偺懱愊偑丄俋俀侽丏係俀們倣3偱偁傞偲偒丄
丂丂挿曽宍俛偺摦偔懍偝傪媮傔傛丅
乮夝乯乮侾乯丂侾侽侽侽亅俈兾
丂兾亖俁丏侾係丂偲偡傟偽丄丂侾侽侽侽亅俈兾亖俋俈俉丏侽俀乮們倣3乯丂偱偁傞丅
乮俀乯丂俁昩屻偼丄
丂丂丂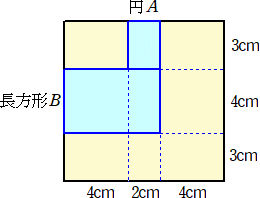
偲側傞偺偱丄媮傔傞懱愊偼丄丂侾侽侽侽亅俁兾亅係俉亖俋俆俀亅俁兾
丂兾亖俁丏侾係丂偲偡傟偽丄丂俋俆俀亅俁兾亖俋係俀丏俆俉乮們倣3乯丂偱偁傞丅
丂俆昩屻偼丄
丂丂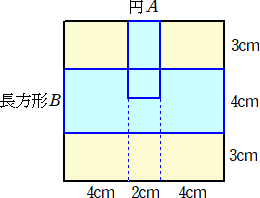
偲側傞偺偱丄媮傔傞懱愊偼丄丂侾侽侽侽亅俆兾亅俉侽亄乮兾/俀乯亊俀亖俋俀侽亅係兾
丂兾亖俁丏侾係丂偲偡傟偽丄丂俋俀侽亅係兾亖俋侽俈丏係係乮們倣3乯丂偱偁傞丅
乮俁乯丂俉昩屻偼丄
丂丂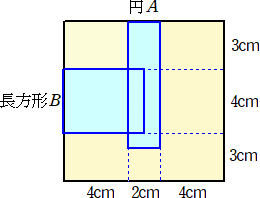
偲側傞偺偱丄媮傔傞懱愊偼丄丂侾侽侽侽亅俉兾亅係侽亄乮兾/係乯亊係亖俋俇侽亅俈兾
丂兾亖俁丏侾係丂偲偡傟偽丄丂俋俇侽亅俈兾亖俋俁俉丏侽俀乮們倣3乯丂偱偁傞丅
乮係乯丂挿曽宍俛偺摦偔懍偝傪昩懍 倶 們倣偲偡傞丅
丂挿曽宍俛傪峫偊側偄応崌丄懱愊偼丄丂侾侽侽侽亅俋兾亖俋俈侾丏俈係乮們倣3乯丂偱丄
丂丂俋俈侾丏俈係亅俋俀侽丏係俀亖俆侾丏俁俀乮們倣3乯丂偩偗懡偄丅
丂挿曽宍俛偑摦偄偰丄墌俙偑摦偄偨晹暘偵傇偮偐傞偲偒丄偦偺懱愊偼丄俁俀們倣3
丂挿曽宍俛偑摦偄偰丄墌俙偑摦偄偨晹暘傪娧捠偟偰弌傞傑偱傪峫偊傞偲丄偦偺偲偒偺懱愊偼丄
丂丂侾侽侽侽亅俋兾亅係俉亄乮兾/俀乯亊係亖俋俆俀亅俈兾亖俋俁侽丏侽俀乮們倣3乯
丂傛偭偰丄丂俋俁侽丏侽俀亅俋俀侽丏係俀亖俋丏俇乮們倣3乯丂偩偗丄挿曽宍俛傪偝傜偵摦偐偣偽傛偄丅
丂俋丏俇亐俉亖侾丏俀乮們倣乯丂傛傝丄俋昩娫偱丄挿曽宍俛偼丄俈丏俀們倣丂摦偔偺偱丄挿曽宍俛偺昩懍
偼丄丂俈丏俀亐俋亖侽丏俉乮們倣乯丂偲側傞丅丂丂乮廔乯
乮僐儊儞僩乯丂嵟屻偺乮係乯偼丄乮俁乯偺傛偆偵挿曽宍俛偑墌俙偺拞偵巭傑傞壜擻惈傕峫偊傜傟傑偟
丂丂丂丂丂丂偨偑丄偦傟偼側偄偲偄偆偙偲偱埨怱偟傑偟偨丅偦偺揰丄栤戣偑椙怱揑偱偟偨偹丅
乮捛婰乯丂椷榓俆擭俀寧侾侽擔晅偗
丂椷榓俆擭俀寧俈擔乮壩乯晅偗挬擔怴暦挬姧偵椷榓俆擭搙奐惉拞妛擖帋栤戣偑宖嵹偝傟偨丅
塡偵傛傞偲丄栤戣偑堈偟偡偓偰丄俈妱俆暘偲偭偰傕棊偪傞偐傕丏丏丏偲偺偙偲丅偳傫側栤戣偐嫽
枴偑偁傝丄偄偔偮偐柺敀偦偆側栤戣傪峫偊偰傒偨丅
侾丏丂僂僒僊偲僇儊偑嫞憟偟偨丅僇儊偼僗僞乕僩抧揰偐傜僑乕儖抧揰傑偱枅暘係倣偺懍偝偱憱傝
丂丂懕偗傞丅僂僒僊偼僗僞乕僩抧揰傪僇儊偲摨帪偵弌敪偟丄枅暘俇侽倣偺懍偝偱憱偭偰偄偨偑丄
丂丂僑乕儖抧揰傑偱巆傝侾侽侽倣偵側偭偨偲偙傠偱憱傞偺傪傗傔偰丄拫怮傪巒傔偨丅拫怮傪巒傔
丂丂偨俇侽暘屻偵栚傪妎傑偟偨僂僒僊偼丄僇儊偵捛偄敳偐傟偰偄傞偙偲偵婥偑偮偄偨丅偁傢偰偨
丂丂僂僒僊偼丄偦偙偐傜枅暘俉侽倣偺懍偝偱僑乕儖抧揰傑偱憱偭偨偑丄僂僒僊偑僑乕儖抧揰偵
丂丂拝偄偨偺偼丄僇儊偑僑乕儖抧揰偵拝偄偨帪崗偺俆昩屻偩偭偨丅偙偺偲偒丄師偺栤偄偵摎偊
丂丂傛丅
乮侾乯丂僂僒僊偑拫怮傪巒傔偰偐傜僇儊偑僑乕儖抧揰偵拝偔傑偱偺帪娫偼壗暘壗昩偐丅
乮俀乯丂僂僒僊偑拫怮傪巒傔偨偲偒丄僂僒僊偼僇儊傛傝壗倣愭偵偄偨偐丅
乮俁乯丂僗僞乕僩抧揰偐傜僑乕儖抧揰傑偱偺摴偺傝偼壗倣偐丅
丂丂
乮夝乯乮侾乯丂僂僒僊偑侾侽侽倣傪暘懍俉侽倣偱憱傞偺偵梫偡傞帪娫偼丄丂侾侽侽亐俉侽亖俆/係乮暘乯
丂丂昩偵姺嶼偟偰丄丂乮俆/係乯亊俇侽亖俈俆乮昩乯
丂傛偭偰丄僂僒僊偑拫怮偐傜栚偑妎傔憱傝巒傔偰偐傜僇儊偑僑乕儖抧揰偵拝偔傑偱偺帪娫偼丄
丂俈俆-俆亖俈侽乮昩乯丂偲側傞丅偟偨偑偭偰丄僂僒僊偑拫怮傪巒傔偰偐傜僇儊偑僑乕儖抧揰偵拝
偔傑偱偺帪娫偼丄丂俇侾暘侾侽昩丂偱偁傞偙偲偑暘偐傞丅
乮俀乯丂僇儊偼丄僂僒僊偑拫怮傪巒傔偰偐傜丄俇侾暘侾侽昩偱僑乕儖抧揰偵拝偔偺偱丄偦偺娫偺
丂摴偺傝偼丄丂乮俇侾亄侾/俇乯亊係亖俀係係亄俀/俁乮倣乯丂側偺偱丄僂僒僊偑拫怮傪巒傔偨偲偒丄
丂僂僒僊偼僇儊傛傝丄丂俀係係亄俀/俁亅侾侽侽亖侾係係亄俀/俁乮倣乯丂愭偵偄偨丅
乮俁乯丂僂僒僊偑僗僞乕僩抧揰傪弌敪偟丄拫怮傪巒傔傞傑偱偺帪娫傪 倲 暘偲偡傞偲丄
丂丂俇侽倲亖係倲亄侾係係亄俀/俁丂偡側傢偪丄丂俆俇倲亖係俁係/俁丂傛傝丄丂倲亖俁侾/侾俀乮暘乯
丂傛偭偰丄僗僞乕僩抧揰偐傜僑乕儖抧揰傑偱偺摴偺傝偼丄
丂丂侾侽侽亄俇侽亊乮俁侾/侾俀乯亖俀俆俆乮倣乯丂丂乮廔乯
乮僐儊儞僩乯丂乽僂僒僊偲僇儊乿偺偲偰傕柺敀偄栤戣偱偟偨丅
俀丏丂侾曈偺挿偝偑侾們倣偺惓榋妏宍俙俛俠俢俤俥偺廃忋偵丄師偺傛偆側揰俹丄俻偑偁傞丅
丂丒揰俹偼曈俙俥忋偵偁傝丄俙俹 丗 俹俥亖侾 丗 俀丂偱偁傞丅
丂丒揰俻偼捀揰俙傪弌敪偟丄惓榋妏宍偺廃忋傪斀帪寁夞傝偵暘懍侾們倣偱摦偔丅揰俻偼丄捀揰
丂丂俛丄俠丄俢丄俤傪偙偺弴偱捠傝丄捀揰俙傪弌敪偟偨俆暘屻偵捀揰俥偱巭傑傞丅
丂丂丂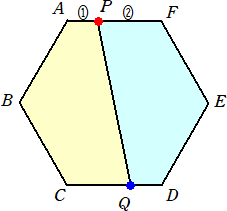
丂揰俻偑捀揰俙傗捀揰俥偵偄傞偲偒傪彍偄偰丄惓榋妏宍偼捈慄俹俻偵傛偭偰俀偮偺晹暘偵暘
偗傜傟傞丅偙偺俀偮偺晹暘偺偆偪丄堦曽偺柺愊偑懠曽偺柺愊偺俀攞偵側傞偺偼丄揰俻偑捀揰
俙傪弌敪偟偰偐傜壗暘壗昩屻偐丅
乮夝乯丂惓榋妏宍偺柺愊傪侾偲偟偰丄柺愊偑丂侾/俁丂偲丂俀/俁丂偵暘偗傞揰傪扵偣偽傛偄丅
丂惓榋妏宍傪壓恾偺傛偆偵暘妱偡傞丅
丂丂丂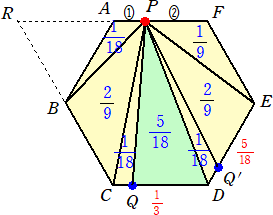
丂仮俙俛俥亖侾/俇丂側偺偱丄丂仮俹俙俛亖乮侾/俇乯亊乮侾/俁乯亖侾/侾俉
摨條偵偟偰丄丂仮俹俤俥亖乮侾/俇乯亊乮俀/俁乯亖侾/俋
丂師偵丄惓嶰妏宍俙俛俼乮柺愊亖侾/俇乯傪峫偊丄仮俹俛俠亖侾/俇亄侾/侾俉亖俀/俋
丂傑偨丄仮俹俠俢亖乮侾/俇乯亊俀亖侾/俁丂偱丄仮俹俠俻亖侾/侾俉丂偲側傞揰俻傪偲傟偽丄偪傚偆偳
丂仮俹俙俛亄仮俹俛俠亄仮俹俠俻亖侾/侾俉亄俀/俋亄侾/侾俉亖侾/俁
偲側傞丅偙偺偲偒丄揰俻偼曈俠俢傪丂侾 丗 俆丂偵撪暘偡傞揰側偺偱丄俙傪弌敪偟偰偐傜俀暘侾侽昩
屻偲側傞丅堦曽偺柺愊偑懠曽偺柺愊偺俀攞偵側傞偺偼丄傕偆侾揰偁傞丅
丂仮俹俢俤亖侾-乮侾/侾俉亄俀/俋亄侾/俁亄侾/俋乯亖俆/侾俉丂側偺偱丄仮俹俻乫俤亖俀/俋丂偲側傞揰俻乫
傪偲傟偽丄偪傚偆偳丂仮俹俤俥亄仮俹俻乫俤亖侾/俋亄俀/俋亖侾/俁丂偲側傞丅
丂偙偺偲偒丄揰俻乫偼丄曈俢俤傪丂侾 丗 係丂偵撪暘偡傞揰側偺偱丄俙傪弌敪偟偰偐傜俁暘侾俀昩屻
偲側傞丅丂丂乮廔乯
乮僐儊儞僩乯丂惓榋妏宍偺暘妱偑柺敀偐偭偨偱偡丅
俁丏丂壓恾偺傛偆偵丄侾曈偺挿偝偑侾侽們倣偺棫曽懱俙俛俠俢-俤俥俧俫偵偍偄偰丄曈俙俢丄俙俤丄
丂丂俛俠丄俛俥忋偵偦傟偧傟揰 俬丄俰丄俲丄俴傪偲傝丄俙俬亖俙俰亖俛俲亖俛俴亖俇們倣偲偡傞丅傑偨丄
丂丂曈俙俤丄俙俛丄俢俫丄俢俠忋偵偦傟偧傟揰俵丄俶丄俷丄俹偑偁傝丄俙俵亖俙俶亖俢俷亖俢俹亖俁們倣
丂丂偱偁傞丅
丂偙偺棫曽懱傪丄係揰 俬丄俰丄俲丄俴傪捠傞暯柺偲係揰俵丄俶丄俷丄俹傪捠傞暯柺偱愗抐偟偰丄係偮
偺棫懱偵愗傝暘偗傞丅捀揰俧傪娷傓彫棫懱傪倃偲偡傞丅
丂丂丂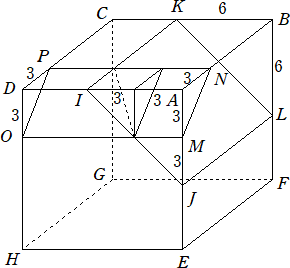
丂偙偺偲偒丄師偺栤偄偵摎偊傛丅
乮侾乯丂棫懱倃偺尒庢傝恾傪彂偗丅
乮俀乯丂棫懱倃偺懱愊傪媮傔傛丅
乮夝乯乮侾乯丂棫懱倃偺尒庢傝恾偼丄
丂丂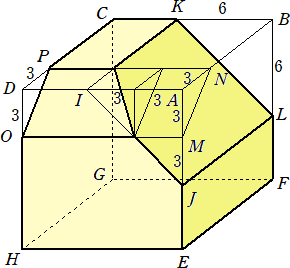
乮俀乯丂棫懱倃偺懱愊偼丄俀偮偺嶰妏悕偺懱愊傪堷偄偰丄偦偺嫟捠晹暘乮壓恾偺悈怓晹暘乯傪
丂丂壛偊傟偽傛偄丅
丂丂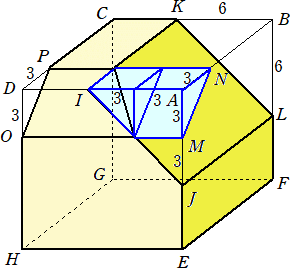
丂傛偭偰丄媮傔傞棫懱倃偺懱愊倁偼丄
倁亖侾侽侽侽亅係丏俆亊侾侽亅侾俉亊侾侽亄乮係丏俆亊俁亄俋亊俁亐俁乯亖俈俋俈丏俆乮們倣3乯
乮僐儊儞僩乯丂忋婰偺夝偱偼丄嫟捠晹暘乮忋恾偺悈怓晹暘乯偺懱愊傪嶰妏拰偲巐妏悕偵暘偗偰
丂丂丂丂丂丂媮傔偨偑丄乽棫懱恾宍偺懱愊乿偺峫偊曽傪梡偄偰丄
丂丂俁亊俁亐俀亊乮俇亄俇亄俁乯/俁亖俀俀丏俆乮們倣3乯
丂偲偟偰傕傛偄丅
係丏丂廃偺挿偝偑俇們倣偺墌偑偁傞丅偙偺墌廃傪俇摍暘偡傞応強傪弴偵俙丄俛丄俠丄俢丄俤丄俥 偲
丂丂偡傞丅偙偺墌廃忋傪枅昩侾們倣偺懍偝偱摦偔俁偮偺揰俹丄俻丄俼 偑偁傞丅
丂俁揰俹丄俻丄俼 偼偦傟偧傟俙抧揰丄俠抧揰丄俤抧揰偐傜摨帪偵摦偒巒傔偰丄俹偲俻偼斀帪寁
廃傝丄俼偼帪寁夞傝偵恑傓丅偦偺屻丄俹丄俻丄俼 偺偆偪偺俀揰偑弌夛偆偨傃偵丄弌夛偭偨俀揰
偼偦傟偧傟捈慜偺帺暘偲偼斀懳岦偒偵摨偠懍偝偱恑傓丅
丂偙偺偲偒丄師偺栤偄偵摎偊傛丅
乮侾乯丂俁揰俹丄俻丄俼 偑摦偒巒傔偰偐傜俇昩屻偵丄俹丄俻丄俼 偑偄傞抧揰偼偳偙偐丅
乮俀乯丂俁揰俹丄俻丄俼 偑摦偒巒傔偰偐傜弶傔偰丄俹丄俻丄俼 偑摨帪偵嵟弶偺埵抲偵摓払偡傞偺
丂丂偼壗昩屻偐丅
乮俁乯丂俁揰俹丄俻丄俼 偑摦偒巒傔偰偐傜侾侽侽昩屻偵丄俹丄俻丄俼 偑偄傞抧揰偼偳偙偐丅
乮係乯丂揰俹偲揰俼偑俋俋夞栚偵弌夛偆偺偼丄俁揰俹丄俻丄俼 偑摦偒巒傔偰偐傜壗昩屻偐丅
乮夝乯乮侾乯丂壓恾偺昞偱丄乽斀乿偼斀帪寁夞傝丄乽帪乿偼帪寁夞傝傪昞偡丅
| 丂 |
| 丂 |
侽 |
侾 |
俀 |
俁 |
係 |
俆 |
俇 |
俈 |
俉 |
俋 |
侾侽 |
侾侾 |
侾俀 |
| 俹斀 |
俙 |
俛 |
俠 |
俛 |
俙 |
俛 |
俠斀 |
俢 |
俠 |
俢 |
俤 |
俥 |
俤帪 |
| 俻斀 |
俠 |
俢 |
俠 |
俢 |
俤 |
俥 |
俤帪 |
俢 |
俤 |
俥 |
俙 |
俥 |
俙斀 |
| 俼帪 |
俤 |
俢 |
俤 |
俥 |
俙 |
俥 |
俙斀 |
俛 |
俠 |
俛 |
俙 |
俛 |
俠斀 |
| 丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
丂 |
| 丂 |
侾俁 |
侾係 |
侾俆 |
侾俇 |
侾俈 |
侾俉 |
| 俹 |
俢 |
俤 |
俥 |
俙 |
俥 |
俙斀 |
| 俻 |
俛 |
俠 |
俛 |
俙 |
俛 |
俠斀 |
| 俼 |
俢 |
俠 |
俢 |
俤 |
俥 |
俤帪 |
|
丂忋婰昞傛傝丄丂俹偼丄俠抧揰丄俻偼丄俤抧揰丄俼偼丄俙抧揰偵偄傞丅
乮俀乯丂俇昩偱墌廃忋傪侾俀侽亱夞揮側偺偱丄俇亊俁亖侾俉乮昩乯屻偵嵟弶偺埵抲偵摓払偡傞丅
丂丂乮偝傜偵丄夞揮偺岦偒傑偱娷傔偰尦偵栠傞偙偲偑丄忋婰偺昞偐傜傕暘偐傞乯
乮俁乯丂侾侽侽亐侾俉亖俆丂丒丒丒丂侾侽丂側偺偱丄忋婰偺昞偺侾侽昩屻偺埵抲偵偄傞偐傜丄
丂丂俹偼丄俤抧揰丄俻偲俼偼丄俙抧揰偵偄傞丅
乮係乯丂嵟弶偺侾俉昩娫偱丄揰俹偲揰俼偑弌夛偆偺偼丄係夞乮係丄俉丄侾俁丄侾俈昩屻乯偁傞偺偱丄
丂俋俋夞弌夛偆偺偼丄丂俋俋亐係亖俀係丂丒丒丒丂俁丂傛傝丄忋婰偺昞偺侾俁昩屻側偺偱丄
丂丂俀係亊侾俉亄侾俁亖係係俆乮昩屻乯丂偲側傞丅丂丂乮廔乯
乮僐儊儞僩乯丂侾俉昩娫偺廃婜惈偵婥偑偮偗偽娙扨偱偟偨丅
俆丏丂侾丄俀丄丒丒丒丄俈偺俈庬椶偺悢帤傪偄偔偮偐暲傋偰嶌傜傟傞惍悢傪俙丄俛偲偡傞丅師偺栤偄
丂丂偵摎偊傛丅
乮侾乯丂俙亄俛亖俋俇丂偲側傞俙丄俛偺慻偼壗捠傝偁傞偐丅
乮俀乯丂俙亄俛亖俋俈侾丂偲側傞俙丄俛偺慻偼壗捠傝偁傞偐丅
乮俁乯丂俙亄俛亖俋俈俀丂偲側傞俙丄俛偺慻偑壗捠傝偁傞偐丅
乮係乯丂俙亄俛亖俋俈俀俁丂偲側傞俙丄俛偺慻偼壗捠傝偁傞偐丅
乮夝乯乮侾乯丂孞傝忋偑傝偑側偄偺偱丄傑偢堦偺埵偺婲偙傝摼傞応崌偼丄
丂乮俙偺堦偺埵丆俛偺堦偺埵乯亖乮侾丆俆乯丄乮俀丆係乯丄乮俁丆俁乯丄乮係丆俀乯丄乮俆丆侾乯丂偺俆捠傝
丂偦偺侾捠傝偵懳偟偰丄廫偺埵偺婲偙傝摼傞応崌偼丄
丂乮俙偺廫偺埵丆俛偺廫偺埵乯亖乮俀丆俈乯丄乮俁丆俇乯丄乮係丆俆乯丄乮俆丆係乯丄乮俇丆俁乯丄乮俈丆俀乯丂偺俇捠傝
傛偭偰丄媮傔傞応崌偺悢偼丄丂俆亊俇亖俁侽乮捠傝乯
乮俀乯丂俋俈侾亖俋俇侽亄侾侾丂側偺偱丄懌偟偰侾侾偲側傞応崌偼丄
丂丂乮係丆俈乯丄乮俆丆俇乯丄乮俇丆俆乯丄乮俈丆係乯丂偺係捠傝偁傞偙偲偐傜丄
丂俙亄俛亖俋俈侾丂偲側傞応崌偺悢偼丄俁侽亊係亖侾俀侽乮捠傝乯
乮俁乯丂俋俈俀亖俋俇侽亄侾俀丂傑偨偼丄丂俋俈俀亖俋俈侽亄俀丂偲峫偊傞偲丄
丂丂懌偟偰侾俀偲側傞応崌偼丄丂乮俆丆俈乯丄乮俇丆俇乯丄乮俈丆俆乯丂偺俁捠傝偁傞偺偱丄
丂丂丂丂俋俇侽亄侾俀丂偲側傞応崌偺悢偼丄丂俁侽亊俁亖俋侽乮捠傝乯
丂丂懌偟偰俀偲側傞応崌偼丄乮侾丆侾乯丂偺侾捠傝
丂丂丂丂俋俈侽亄俀丂偲側傞応崌偺悢傪媮傔傞偨傔偵丄俠亄俢亖俋俈丂偵偮偄偰丄
丂乮俠偺堦偺埵丆俢偺堦偺埵乯亖乮侾丆俈乯丄乮俀丆俇乯丄乮俁丆係乯丄乮係丆俁乯丄乮俆丆俀乯丄乮俇丆侾乯丂偺俇捠傝
丂偦偺侾捠傝偵懳偟偰丄廫偺埵偺婲偙傝摼傞応崌偼丄
丂乮俠偺廫偺埵丆俢偺廫偺埵乯亖乮俀丆俈乯丄乮俁丆俇乯丄乮係丆俆乯丄乮俆丆係乯丄乮俇丆俁乯丄乮俈丆俀乯丂偺俇捠傝
傛偭偰丄俠亄俢亖俋俈丂偲側傞応崌偺悢偼丄丂俇亊俇亖俁俇乮捠傝乯
丂埲忋偐傜丄俙亄俛亖俋俈俀丂偲側傞応崌偺悢偼丄丂俋侽亄俁俇亖侾俀俇乮捠傝乯
乮係乯丂俋俈俀俁亖俋俈俀侽亄俁丂傑偨偼丄丂俋俈俀俁亖俋俈侾侽亄侾俁丂偲峫偊偰丄媮傔傞応崌偺悢偼丄
丂侾俀俇亊俀亄侾俀侽亊俀亖係俋俀乮捠傝乯
乮僐儊儞僩乯丂堈偟偄偲偼尵傢傟偰偄傑偡偑丄偦偙偦偙峫偊偝偣傞椙栤偱偡偹両廫暘妝偟傑偣偰
丂丂丂丂丂丂傕傜偄傑偟偨丅
乮捛婰乯丂椷榓俆擭係寧侾俉擔晅偗
丂拀攇戝妛晬懏拞妛乮俀侽侾係乯偺擖帋栤戣傪攓尒偡傞婡夛偑偁傝丄挧愴偟偰傒偨丅栤戣偼
夵戣偝傟偰偄傑偡丅
栤戣丂俀偮偺惍悢俙丄俛偑偁傝丄俙亜俛偱丄俙偼俛偱妱傝愗傟側偄傕偺偲偡傞丅俙偲俛偺嵟戝岞
丂丂丂栺悢丄嵟彫岞攞悢傪偦傟偧傟 俵偲俴 偲偍偔丅
丂俴亄俵亖俇俉係丂丄俴亅俵亖俇俇侽丂偺偲偒丄俙丄俛偺抣傪媮傔傛丅
乮夝乯丂戣堄傛傝丄丂俴亖俇俈俀丂丄俵亖侾俀丂偱偁傞丅俙亖侾俀倎丂丄俛亖侾俀倐丂乮倎偲倐偼屳偄偵慺乯
偲偍偗偰丄丂侾俀倎倐亖俇俈俀丂傛傝丄丂倎倐亖俆俇丂偲側傞丅
丂倎偲倐偼屳偄偵慺側偺偱丄丂乮倎丆倐乯亖乮俆俇丆侾乯丄乮俉丆俈乯丂偱偁傞偑丄俙偼俛偱妱傝愗傟側偄偙
偲偐傜丄乮倎丆倐乯亖乮俆俇丆侾乯丂偼晄揔
丂傛偭偰丄丂俙亖侾俀亊俉亖俋俇丂丄俛亖侾俀亊俈亖俉係丂丂乮廔乯
乮捛婰乯丂椷榓俇擭俀寧俆擔晅偗
丂椷榓俇擭俀寧係擔乮擔乯晅偗挬擔怴暦挬姧偵椷榓俇擭搙嶗堻拞妛擖帋栤戣偑宖嵹偝傟偨丅
偄偔偮偐柺敀偦偆側栤戣偑偁偭偨偺偱丄彫妛惗偵側偭偨偮傕傝偱峫偊偰傒偨丅
嘥丏乮俀乯丂崟偄娵仠偲敀偄娵仜傪墶俈儅僗偡傋偰偵暲傋傞丅
乮鶣乯丂暲傋曽偺寛傑傝偼師偺乮偁乯乮偄乯乮偆乯乮偊乯偱偁傞丅
乮偁乯丂嘇偲嘋偵偼摨偠怓偺娵偼暲傋側偄丅
乮偄乯丂嘇偲嘐偵偼摨偠怓偺娵傪暲傋傞丅
乮偆乯丂嘍嘐嘑偡傋偰偵摨偠怓偺娵傪暲傋傞偙偲偼偱偒側偄丅
乮偊乯丂嘋偑敀偄娵仜偺偲偒丄嘊偲嘍偺椉曽偲傕偵崟偄娵仠傪暲傋傞偙偲偼偱偒側偄丅
丂偙偺偲偒丄崟偄娵仠偲敀偄娵仜偺暲傋曽偼壗捠傝偁傞偐丅
乮鶤乯丂墶俈儅僗傪壓恾偺傛偆偵係峴暲傋傞丅
丂乮鶣乯偺暲傋曽偺寛傑傝乮偁乯乮偄乯乮偆乯乮偊乯偵師偺乮偍乯偺寛傑傝丗
乮偍乯丂奺峴偺俙丄俛丄俠丄俢偵偼丄俙偲俢偵摨偠怓偺娵丄俛偲俠偵摨偠怓偺娵傪暲傋丄俙偲俛偵偼
丂丂丂摨偠怓偺娵傪暲傋側偄丅
傪壛偊偰丄俀俉儅僗偵崟偄娵仠偲敀偄娵仜傪暲傋傞偲偒丄暲傋曽偼壗捠傝偁傞偐丅
乮夝乯乮鶣乯丂戣堄傛傝丄婲偙傝摼傞応崌偼丄俈儅僗傪暲傋偰丄
丂嘆仜嘊仠仜仜仠
丂嘆仜嘊仠仠仜仜
丂嘆仜嘊仠仠仜仠丂丂丂嘆偲嘊偼俀捠傝偢偮偁傞偺偱丄俀亊俀亊俁亖侾俀乮捠傝乯
丂嘆仠仜仜仠仠仜
丂嘆仠仠仜仜仠仜
丂嘆仠仠仜仜仠仠
丂嘆仠仜仜仜仠仜
丂嘆仠仜仜仜仠仠丂丂丂嘆偼俀捠傝偁傞偺偱丄俀亊俆亖侾侽乮捠傝乯
丂埲忋偐傜丄媮傔傞応崌偺悢偼丄丂侾俀亄侾侽亖俀俀乮捠傝乯
乮鶤乯丂乮鶣乯偺寢壥傪梡偄偰丄媮傔傞応崌偺悢偼丄
丂侾俀亊侾俀亊侾侽亊侾侽亊俀亖俀俉俉侽侽乮捠傝乯丂丂乮廔乯
嘥丏乮俁乯丂侾曈偺挿偝偑侾侽偺惓曽宍偺愜傝巻傪侾杮偺懳妏慄偱愜偭偰捈妏俀摍曈嶰妏宍傪
丂嶌傝丄偝傜偵丄係俆亱偺妏傪帩偮捀揰偑廳側傞傛偆偵愜傞丅偦偺偲偒弌棃傞捈妏俀摍曈嶰妏
丂宍傪丄捈妏偑俁摍暘偝傟傞傛偆偵愜傝丄偼傒弌偰偄傞晹暘傪僴僒儈偱愗傝庢傝丄壓恾偺傛偆
丂側俀摍曈嶰妏宍俙俛俠傪嶌傞丅
 |
丂 |
 |
丂偙偺偲偒丄師偺栤偄偵摎偊傛丅
乮鶣乯丂俀摍曈嶰妏宍俙俛俠偺愜傝巻傪峀偘傞偲偒丄偳傫側恾宍偲側傞偐丅
乮鶤乯丂俙俛亖俀丏俈 偺偲偒丄乮鶣乯偱摼傜傟偨恾宍偺柺愊傪媮傔傛丅
乮鶥乯丂壓恾偺傛偆偵丄俀摍曈嶰妏宍俙俛俠偺撪晹偐傜丄侾曈偺挿偝偑侽丏俇偺惓曽宍偲拞怱偑
丂丂曈俛俠忋偵偁傞捈宎侾偺敿墌傪愗傝庢傞丅
丂丂
丂偙偺愜傝巻傪乮鶣乯偲摨條偵峀偘傞偲偒丄巆偭偨晹暘偺恾宍偺柺愊傪媮傔傛丅
乮夝乯乮鶣乯丂柧傜偐偵丄惓廫擇妏宍偲側傞丅
乮鶤乯丂俀摍曈嶰妏宍俙俛俠偼丄傕偲偺惓曽宍偱峫偊傞偲丄壓恾偺傛偆偱偁傞丅
丂丂
丂忋恾偺仮俙俛俠偺柺愊偼丄丂俀丏俈亊俆亐俀亖俇丏俈俆丂偲側傞偺偱丄媮傔傞恾宍偺柺愊偼丄
丂俇丏俈俆亊侾俀亖俉侾
乮鶥乯丂愗傝庢傜傟傞晹暘偺柺愊偼丄
丂惓曽宍丂丒丒丒丂乮侽丏俇亊侽丏俇乯亊侾俀亖係丏俁俀
丂敿墌丂丒丒丒丂乮兾亊乮侾/俀乯2亐俀乯亊侾俀亖俁兾/俀丂丂偙偙偱丄兾亖俁丏侾係 偲偟偰丄係丏俈侾
偟偨偑偭偰丄媮傔傞恾宍偺柺愊偼丄丂俉侾亅乮係丏俁俀亄係丏俈侾乯亖俈侾丏俋俈丂丂乮廔乯
嘦丏丂摨偠戝偒偝偺偨偔偝傫偺棫曽懱偲丄惵怓偺奊偺嬶侾俀侽倣倢丄墿怓偺奊偺嬶俀侽侽倣倢丄愒
丂怓偺奊偺嬶俀侽侽倣倢偑偁傞丅偙偺奊偺嬶偼崿偤傞偲暿偺怓偑嶌傟傞丅惵怓偲墿怓傪摨偠検
丂崿偤傞偲丄椢怓偑弌棃丄愒怓偲墿怓傪摨偠検崿偤傞偲丄僆儗儞僕怓偑弌棃丄惵怓偲墿怓傪
丂侾丗俀偺妱崌偱崿偤傞偲丄墿椢怓偑弌棃傞丅
丂崱丄偙偺奊偺嬶偱棫曽懱偺俇柺傪揾傞丅偨偩偟丄奊偺嬶偼偡傋偰巊偆偲偼尷傜側偄丅偙偺奊
偺嬶偼偳偺怓傕侾侽倣倢偱棫曽懱偺俇/俆柺傪揾傞偙偲偑弌棃傞丅師偺栤偄偵摎偊傛丅
乮侾乯丂偙偺棫曽懱偺侾柺傪揾傞偺偵昁梫側奊偺嬶偺検傪媮傔傛丅
乮俀乯丂偙偺棫曽懱偺俇柺偡傋偰傪侾怓偱揾傞偲偒丄
丂乮鶣乯丂俇柺偡傋偰偑愒怓偱揾傜傟偨棫曽懱偼丄嵟戝壗屄偱偒傞偐丅
丂乮鶤乯丂俇柺偡傋偰偑墿椢怓偱揾傜傟偨棫曽懱偼丄嵟戝壗屄偱偒傞偐丅
乮俁乯丂偙偺棫曽懱偺俇柺傪俁柺偢偮摨偠怓偱揾傞丅僆儗儞僕怓偲椢怓偺俀怓偱俁柺偢偮揾傜傟
丂偨棫曽懱偼丄嵟戝壗屄偱偒傞偐丅
乮係乯丂偙偺棫曽懱偺俇柺傪侾柺偢偮惵怓丄墿怓丄愒怓丄椢怓丄僆儗儞僕怓丄墿椢怓偱揾傞丅
乮鶣乯丂偙偺傛偆側棫曽懱偼嵟戝壗屄偱偒傞偐丅
乮鶤乯丂偙偺傛偆側棫曽懱傪嵟傕懡偔偮偔偭偨偲偒丄巊傢側偐偭偨惵怓偺奊偺嬶偺検傪媮傔傛丅
乮夝乯乮侾乯丂侾侽亐俇/俆亖俀俆/俁乮倣倢乯
乮俀乯乮鶣乯丂俀侽侽亐乮俀俆/俁乯亖俀係乮柺乯偐傜丄俀係亐俇亖係乮屄乯偺棫曽懱傪揾傞偙偲偑弌棃傞丅
乮鶤乯丂惵怓侾侽侽倣倢丄墿怓俀侽侽倣倢偱丄墿椢怓俁侽侽倣倢偑弌棃傞偺偱丄
丂俁侽侽亐乮俀俆/俁乯亖俁俇乮柺乯偐傜丄俁俇亐俇亖俇乮屄乯偺棫曽懱傪揾傞偙偲偑弌棃傞丅
乮俁乯丂侾柺摉偨傝偵揾傞奊偺嬶偺検傪寁嶼偡傞丅
丂僆儗儞僕怓丂丒丒丒丂愒怓俀俆/俇倣倢丄墿怓俀俆/俇倣倢
丂椢怓丂丒丒丒丂惵怓俀俆/俇倣倢丄墿怓俀俆/俇倣倢
傛傝丄丂惵怓俀俆/俇倣倢丄愒怓俀俆/俇倣倢丄墿怓俀俆/俁倣倢丂偱棫曽懱偺俀柺偑揾傜傟傞丅
丂侾俀侽亐乮俀俆/俇乯亖侾係係/俆乮亖俀俉丏俉乯
丂俀侽侽亐乮俀俆/俇乯亖係俉
丂俀侽侽亐乮俀俆/俁乯亖俀係
傛傝丄嵟彫偺俀係柺偵拝栚偟偰丄丂俀係亐乮俇亐俀乯亖俉乮屄乯偺棫曽懱傪揾傞偙偲偑弌棃傞丅
乮係乯乮鶣乯乮俁乯偲摨條偵丄侾柺摉偨傝偵揾傞奊偺嬶偺検傪寁嶼偡傞丅
丂惵怓丂丒丒丒丂俀俆/俁倣倢
丂愒怓丂丒丒丒丂俀俆/俁倣倢
丂墿怓丂丒丒丒丂俀俆/俁倣倢
丂椢怓丂丒丒丒丂惵怓俀俆/俇倣倢丄墿怓俀俆/俇倣倢
丂僆儗儞僕怓丂丒丒丒丂愒怓俀俆/俇倣倢丄墿怓俀俆/俇倣倢
丂墿椢怓丂丒丒丒丂惵怓俀俆/俋倣倢丄墿怓俆侽/俋倣倢
傛傝丄丂惵怓俀俆/俁亄俀俆/俇亄俀俆/俋亖俀俈俆/侾俉乮倣倢乯丂偱丄
丂侾俀侽亐乮俀俈俆/侾俉乯亖係俁俀/俆俆乮亖俈丏俉俆丒丒丒乯
丂愒怓俀俆/俁亄俀俆/俇亖俈俆/俇乮倣倢乯丂偱丄
丂俀侽侽亐乮俈俆/俇乯亖侾俇
丂墿怓俀俆/俁亄俀俆/俇亄俀俆/俇亄俆侽/俋亖俀侽侽/俋乮倣倢乯丂偱丄
丂俀侽侽亐乮俀侽侽/俋乯亖俋
偱棫曽懱偑揾傜傟傞丅
丂忋婰偺寁嶼傛傝丄惵怓偺検偺惂尷偐傜丄嵟戝俈屄傑偱揾傞偙偲偑偱偒傞丅
乮鶤乯丂巊傢側偐偭偨惵怓偺奊偺嬶偺検偼丄
丂乮俀俈俆/侾俉乯亊乮係俁俀/俆俆亅俈乯亖俀俁俆/侾俉乮倣倢乯丂丂乮廔乯
嘨丏丂侾曈偑侾偺惓嶰妏宍俙俛俠偲侾曈偑俁偺惓曽宍俹俻俼俿偑偁傞丅惓嶰妏宍俙俛俠偺柺愊傪
丂俽偲偍偔丅
丂丂
乮侾乯丂惓嶰妏宍俙俛俠傪忋恾偺埵抲偐傜惓曽宍俹俻俼俿偺撪晹傪偡傋傜側偄傛偆偵夞揮偝偣偰
丂丂傕偲偺埵抲傑偱堏摦偝偣傞丅偙偺偲偒丄惓嶰妏宍俙俛俠偑捠夁偟偨晹暘偺柺愊傪俽傪梡偄偰
丂丂昞偣丅
乮俀乯丂惓嶰妏宍俙俛俠傪丄壓恾偺傛偆偵惓曽宍俹俻俼俿偺乮偄乯偺埵抲偵偍偔丅
丂丂
丂偙偺惓嶰妏宍俙俛俠傪丄惓曽宍俹俻俼俿偺撪晹傪偡傋傜側偄傛偆偵夞揮偝偣側偑傜乮偆乯偺埵抲
傑偱堏摦偝偣傞丅俹俻偵娭偟偰懳徧堏摦偟丄乮偊乯偺埵抲偵堏摦偝偣傞丅偝傜偵丄惓曽宍俹俻俼俿
偺奜晹傪偡傋傜側偄傛偆偵夞揮偝偣側偑傜乮偍乯偺埵抲傑偱堏摦偝偣傞丅崱搙偼丄俼俻偵娭偟偰
懳徧堏摦偟丄乮偐乯偺埵抲偵堏摦偝偣傞丅嵞傃丄惓曽宍俹俻俼俿偺撪晹傪偡傋傜側偄傛偆偵夞揮
偝偣側偑傜乮偒乯偺埵抲傑偱堏摦偝偣傞丅摨偠傛偆偵丄乮偔乯偺埵抲傊愜傝曉偟丄惓曽宍俹俻俼俿偺
奜晹傪偡傋傜側偄傛偆偵夞揮偝偣側偑傜乮偗乯偺埵抲傑偱堏摦偝偣傞丅
丂偙偺偲偒丄揰俠偑偊偑偄偨嬋慄偱埻傑傟偨恾宍偺柺愊傪媮傔傛丅
乮夝乯乮侾乯丂幚嵺偵夞揮偝偣偰壓恾傪摼傞丅
丂丂
丂媮傔傞柺愊偼丄惓嶰妏宍俙俛俠偑係屄暘偲侾曈偑侾偺惓曽宍係屄暘偲敿宎偑侾偱拞怱妏俁侽亱
偺愵宍俉屄暘側偺偱丄丂係俽亄係亄乮俀/俁乯兾丂丂偲側傞丅
丂兾亖俁丏侾係丂偲偟偰丄丂係俽亄係亄乮俀/俁乯兾亖係俽亄係俆俈/俈俆
乮俀乯丂幚嵺偵夞揮偝偣偰壓恾傪摼傞丅揰俠偑偊偑偄偨嬋慄偼愒慄晹暘偱偁傞丅
丂丂
丂媮傔傞柺愊偼丄墿怓偄晹暘偑憡嶦偝傟傞偙偲偵拲堄偟偰丄
丂乮侾曈偑俁偺惓曽宍偺柺愊乯
丂亅乮敿宎偑侾偱拞怱妏俁侽亱偺愵宍俀屄暘乯亄乮敿宎偑侾偱拞怱妏俀侾侽亱偺愵宍俀屄暘乯
亖乮侾曈偑俁偺惓曽宍偺柺愊乯亄乮敿宎偑侾偱拞怱妏侾俉侽亱偺愵宍俀屄暘乯
亖乮侾曈偑俁偺惓曽宍偺柺愊乯亄乮敿宎偑侾偺墌偺柺愊乯
亖俋亄兾
丂兾亖俁丏侾係丂偲偟偰丄媮傔傞柺愊偼丄丂侾俀丏侾係丂丂乮廔乯
乮僐儊儞僩乯丂挿偄暥復戣偱撉傒夝偔偺偑戝曄偱偁傞偑丄幚嵺偵奊傪昤偗偽夝偒傗偡偔側傞偩
丂丂丂丂丂傠偆丅
乮捛婰乯丂椷榓俇擭俀寧俋擔晅偗
丂椷榓俇擭俀寧俇擔乮壩乯晅偗挬擔怴暦挬姧偵椷榓俇擭搙奐惉拞妛擖帋栤戣偑宖嵹偝傟偨丅
偄偔偮偐柺敀偦偆側栤戣偑偁偭偨偺偱丄彫妛惗偵側偭偨偮傕傝偱峫偊偰傒偨丅
侾丏乮侾乯丂悢帤 侾乣俋 偲巐懃墘嶼偺婰崋 亄丄亅丄亊丄亐 偲僇僢僐偩偗傪梡偄偰丄俀侽俀係傪嶌
丂丂丂傞幃傪侾偮彂偗丅偨偩偟丄師偺巜帵偵廬偆偙偲丅
乮鶣乯丂侾偮偺悢帤傪俀屄埲忋巊偭偰偼偄偗側偄丅
乮鶤乯丂俀屄埲忋偺悢帤傪暲傋偰俀寘埲忋偺悢傪嶌偭偰偼偄偗側偄丅
乮鶥乯丂偱偒傞偩偗巊偆悢帤偺屄悢傪彮側偔偣傛丅乮巊偆悢帤偺屄悢偑彮側偄傎偳崅摼揰乯
乮夝乯丂俀侽俀係傪慺場悢暘夝偟偰丄丂俀侽俀係亖俀亊俀亊俀亊侾侾亊俀俁
丂偙傟傛傝丄俀侽俀係亖俉亊乮俀亄俋乯亊乮係亊俇亅侾乯丂偑巚偄偮偔偑丄悢帤偺屄悢偑俇屄傕偁傞丅
丂俀侽俀係亐俉亖俀俆俁丂側偺偱丄悢帤 侾乣俈丄俋 傪梡偄偰丄俀俆俁傪嶌傞偙偲傪峫偊傞偲丄
丂俀俆俁亐乮俋亊俈乯亖係丂丒丒丒丂侾丂偐傜丄丂俀俆俁亖係亊俈亊俋亄侾丂側偺偱丄
丂俀侽俀係亖俉亊乮係亊俈亊俋亄侾乯丂偲側傝丄悢帤偺屄悢偑俆屄偱嵪傓丅
傑偨丄丂俀侽俀係亖係亊侾侾亊係俇丂傛傝丄
丂俀侽俀係亖係亊乮俁亄俉乯亊乮俆亊俋亄侾乯丂偑巚偄偮偔偑丄悢帤偺屄悢偑俇屄傕偁傞丅
偙傟傕丄丂俀侽俀係亖係亊俆侽俇丂偲峫偊偰丄丄悢帤 侾乣俁丄係乣俋 傪梡偄偰丄俆侽俇傪嶌傞偙偲傪
峫偊傞偲丄丂俆侽俇亐乮俋亊俉乯亖俈丂丒丒丒丂俀丂偐傜丄丂俆侽俇亖俈亊俉亊俋亄俀丂側偺偱丄
丂俀侽俀係亖係亊乮俈亊俉亊俋亄俀乯丂偲側傝丄悢帤偺屄悢偑俆屄偱嵪傓丅
埲忋偐傜丄俀侽俀係亖俉亊乮係亊俈亊俋亄侾乯丂傗丂俀侽俀係亖係亊乮俈亊俉亊俋亄俀乯丂側偳丂丂乮廔乯
乮僐儊儞僩乯丂僷僘儖仌僋僀僘偺乽俀侽俀係擭乿傪嶲峫偵偡傞偲丄
丂亅侾亅俆亅俇亄係亊乮俀亄俁亄俈亊俉亊俋乯亖俀侽俀係丂傪偄偠偭偰丄
丂亅俁亊係亄係亊乮俆亄俈亊俉亊俋乯亖係亊乮俀亄俈亊俉亊俋乯亖俀侽俀係丂丒丒丒丂悢帤偺屄悢偑俆屄
偑摼傜傟傞丅
丂傛偍偡偗偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭俀寧侾侾擔晅偗乯
丂忋婰偺栤戣偱丄巊偆悢帤偑係屄埲壓偱 俀侽俀係傪嶌傞幃偼尒偮偐傝傑偣傫偱偟偨丅傛偭偰丄
忋婰偺忦審側傜丄嵟彮偼俆屄偱娫堘偄柍偄偲巚偄傑偡丅
侾丏乮俀乯丂俀杮偺嬥懏朹俷丄俹偑偁傝丄挿偝偼丄俹偺曽偑俷傛傝俀cm挿偔丄廳偝偼丄俀杮偲傕摨偠
丂丂偱偁傞丅挿偝侾們倣偁偨傝偺廳偝偼丄俷偼偳偙偱傕侾們倣偁偨傝侾侽倗偱偁傞偑丄俹偼丄拞娫偺
丂偁傞挿偝偺晹暘偩偗侾們倣偁偨傝侾侾倗偱丄偦傟埲奜偺晹暘偼侾們倣偁偨傝俉倗偱偁傞偲偄偆丅
丂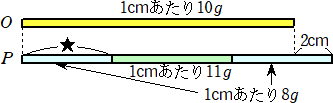
丂俀杮偺嬥懏朹傪忋恾偺嵍抂偐傜摨偠挿偝偩偗愗傝庢傞偲偒丄愗傝庢傞晹暘偺廳偝偑摍偟偔
側傞偺偼丄愗傝庢傞挿偝偑俁係丏俆們倣偺偲偒偩偗偱偁傞丅偙偺偲偒丄師偺栤偄偵摎偊傛丅
(傾)丂忋恾偺仛偺晹暘偺挿偝傪媮傔傛丅
(僀)丂嬥懏朹侾杮偺廳偝傪媮傔傛丅
乮夝乯乮傾乯丂戣堄傛傝丄俉亊仛亄侾侾亊乮俁係丏俆亅仛乯亖侾侽亊俁係丏俆丂側偺偱丄
丂俁亊仛亖俁係丏俆丂傛傝丄丂仛亖侾侾丏俆乮們倣乯
乮僀乯丂愗傝庢傞晹暘偺廳偝偑摍偟偔側傞偺偼丄愗傝庢傞挿偝偑俁係丏俆們倣偺偲偒偩偗偱偁傞偺
丂偱丄俁係丏俆們倣傛傝塃懁偱偼丄俹偼侾們倣偁偨傝俉倗偲側傞丅
丂傛偭偰丄俷偺挿偝傪俴偲偍偔偲丄戣堄傛傝丄侾侽亊乮俴亅俁係丏俆乯亖俉亊乮俴亄俀亅俁係丏俆乯丂側偺偱丄
丂俀亊乮俴亅俁係丏俆乯亖侾俇丂傛傝丄丂俀俴亖俉俆丂傛偭偰丄丂俴亖係俀丏俆乮們倣乯丂偲側傞丅
丂偟偨偑偭偰丄嬥懏朹侾杮偺廳偝偼丄丂侾侽亊係俀丏俆亖係俀俆乮倗乯丂偱偁傞丅丂丂乮廔乯
侾丏乮俁乯丂侾曈俁們倣偺惓嶰妏宍俹偵丄儅乕僋俹偑偐偐傟偰偄傞丅偙偺惓嶰妏宍俹偑偼偠傔壓偺
丂丂恾偺僗僞乕僩偺埵抲偵偁偭偰丄侾曈俋們倣偺惓嶰妏宍俻偺奜廃傪恾偺栴報偺曽岦偵偡傋傜
丂丂側偄傛偆偵揮偑偭偰丄偼偠傔偰僑乕儖偺埵抲偵偔傞傑偱摦偔丅偙偺偲偒丄師偺栤偄偵摎偊傛丅
丂丂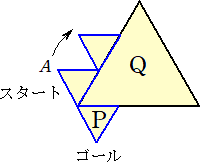
乮傾乯丂惓嶰妏宍俹偑僑乕儖偺埵抲偵拝偄偨偲偒丄儅乕僋俹偼忋偺恾偺岦偒偵側偭偰偄偨丅儅乕
丂僋俹偼丄僗僞乕僩偺埵抲偱偼偳偺岦偒偵偐偐傟偰偄偨偐丅
(僀)丂惓嶰妏宍俹偑僗僞乕僩偐傜僑乕儖傑偱摦偔偲偒丄恾偺捀揰A偑摦偔嫍棧傪媮傔傛丅
(僂)丂惓嶰妏宍俹偑僗僞乕僩偐傜僑乕儖傑偱摦偔偲偒偵捠夁偡傞晹暘偺柺愊偼丄敿宎偑俁們倣偱丄
丂拞怱妏偑俇侽亱偺偍偆偓宍偺柺愊偲丄侾曈偑俁們倣偺惓嶰妏宍偺柺愊傪偦傟偧傟壗屄暘偁
丂傢偣偨傕偺偱偁傞偐丅
乮夝乯乮傾乯丂戣堄傛傝丄壓恾傪摼傞丅
丂丂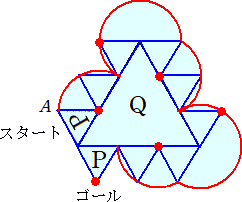
乮僀乯丂俇兾亊乮侾/俁乯亄俇兾亊乮俀/俁乯亄俇兾亊乮侾/俁乯亄俇兾亊乮俀/俁乯亄俇兾亊乮侾/俁乯
丂丂亖侾係兾丂偙偙偱丄兾亖俁丏侾係丂偲偟偰丄丂侾係兾亖係俁丏俋俇乮們倣乯
乮僂乯丂媮傔傞柺愊偼丄壓恾偺愒慄偱埻傑傟偨晹暘偺柺愊乮惓嶰妏宍俻傪彍偔乯偵摍偟偄丅
丂丂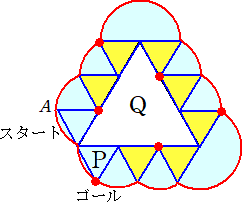
丂忋恾傛傝丄敿宎偑俁們倣偱丄拞怱妏偑俇侽亱偺偍偆偓宍偺柺愊傪侾係屄暘偲丄侾曈偑俁們倣偺惓
嶰妏宍偺柺愊傪俈屄暘偁傢偣偨傕偺偵摍偟偄丅丂丂乮廔乯
乮僐儊儞僩乯丂崱擭搙偺嶗堻拞妛偱傕摨庯巪偺栤戣偑弌戣偝傟傑偟偨丅
俀丏丂俋枃偺僇乕僪 侾丄俀丄俁丄係丄俆丄俇丄俈丄俉丄俋 偑偁傞丅偼偠傔偵丄俋枃偺僇乕僪偐傜壗枃偐
丂傪慖傃丄崿偤崌傢偣偰侾偮偺嶳偵廳偹傞丅偙偺偲偒偺僇乕僪偺暲傃曽傪乽偼偠傔偺僇乕僪偺
丂忬嫷乿偲偄偆偙偲偵偡傞丅
丂偨偲偊偽丄俆枃偺僇乕僪 侾丄俀丄俁丄係丄俆 偑忋偐傜 係丄俀丄俆丄侾丄俁 偺弴偵廳偹傜傟偰偄傞偲
偒偑丄偼偠傔偺僇乕僪偺忬嫷偱丄娙扨偵 亂係俀俆侾俁亃 偲昞偡偙偲偵偡傞丅
丂婘偲敔偑偁傞丅師偺儖乕儖偵廬偭偰丄嶳偵廳偹偨僇乕僪傪忋偐傜侾枃偢偮丄婘偺忋偐丄敔
偺拞偵摦偐偡丅
丒侾枃栚偺僇乕僪偼昁偢婘偺忋偵抲偔丅
丒俀枃栚埲崀偺僇乕僪偼丄偦偺僇乕僪偵彂偐傟偨悢偑婘偺忋偵偁傞偳偺僇乕僪偵彂偐傟偨悢
傛傝傕彫偝偄偲偒偩偗婘偺忋偵抲偒丄偦偆偱側偄偲偒偵偼敔偺拞偵擖傟傞丅
丂偨偲偊偽丄亂係俀俆侾俁亃偺偲偒丄忋婰偺憖嶌偱丄婘偺忋偵偼丄係丄俀丄侾 偺傒偑巆傞丅偙傟傪丄
僇乕僪偑抲偐傟偨弴偵乻係俀侾乼偲昞偡偙偲偵偡傞丅偙偺偲偒丄師偺栤偄偵摎偊傛丅
乮侾乯丂俈枃偺僇乕僪 侾丄俀丄俁丄係丄俆丄俇丄俈 傪巊偆応崌傪峫偊傞丅偼偠傔偺僇乕僪偺忬嫷偑
丂丂亂俈係俇俁侾俀俆亃偱偁傞偲偒偺寢壥傪摎偊傛丅
乮俀乯丂師偺偦傟偧傟偺応崌偺偼偠傔偺僇乕僪偺忬嫷偵偮偄偰摎偊傛丅
(傾)丂俁枃偺僇乕僪 侾丄俀丄俁 傪巊偆応崌傪峫偊傞丅寢壥偑乻俀侾乼偵側傞偼偠傔偺僇乕僪偺忬嫷
丂傪偡傋偰彂偒弌偣丅
(僀)丂係枃偺僇乕僪 侾丄俀丄俁丄係 傪巊偆応崌傪峫偊傞丅寢壥偑乻俀侾乼偵側傞偼偠傔偺僇乕僪偺忬
丂嫷傪偡傋偰彂偒弌偣丅
(僂)丂俆枃偺僇乕僪 侾丄俀丄俁丄係丄俆 傪巊偆応崌傪峫偊傞丅
丂乮鶣乯丂寢壥偑乻俀侾乼偵側傞偼偠傔偺僇乕僪偺忬嫷偼壗捠傝偁傞偐丅
丂乮鶤乯丂寢壥偑乻俆俀侾乼偵側傞偼偠傔偺僇乕僪偺忬嫷偼壗捠傝偁傞偐丅
(僄)丂俇枃偺僇乕僪 侾丄俀丄俁丄係丄俆丄俇 傪巊偆応崌傪峫偊傞丅寢壥偑乻俆俀侾乼偵側傞偼偠傔偺僇
丂乕僪偺忬嫷偼壗捠傝偁傞偐丅
乮俁乯丂俋枃偺僇乕僪慡晹傪巊偆応崌傪峫偊傞丅寢壥偑乻俈俆係俀侾乼偵側傞偼偠傔偺僇乕僪偺忬嫷
丂偼壗捠傝偁傞偐丅
乮夝乯乮侾乯丂柧傜偐偵丄乻俈係俁侾乼丂偲側傞丅
乮俀乯乮傾乯丂亂俀侾俁亃丄亂俀俁侾亃丂偱偁傞丅
乮僀乯丂亂俀侾俁係亃丄亂俀侾係俁亃丄亂俀俁侾係亃丄亂俀係侾俁亃丄亂俀俁係侾亃丄亂俀係俁侾亃丂偱偁傞丅
乮僂乯乮鶣乯丂俀侾***丂丄俀*侾**丂丄俀**侾*丂丄俀***侾丂偺偦傟偧傟偱丄*** 偵偼丄俁丄係丄俆 偺壗
丂傟偐偑暲傇偺偱丄媮傔傞応崌偺悢偼丄丂係亊俁両亖俀係乮捠傝乯
乮暿夝乯丂俀侾偺暲傃偵丄俁偲係傪捛壛偟偰丄婲偙傝偆傞応崌偼丄乮俀乯乮僀乯傛傝丄
丂俀侾俁係丂丄俀侾係俁丂丄俀俁侾係丂丄俀係侾俁丂丄俀俁係侾丂丄俀係俁侾
丂偦傟偧傟偵丄俆偺擖傟応強傪峫偊偰丄
丂丂俀係俁侾丂偺応崌丄丂俀俆係俁侾丂丄俀係俆俁侾丂丄俀係俁俆侾丂丄俀係俁侾俆
丂丂俀俁係侾丂偺応崌丄丂俀俆俁係侾丂丄俀俁俆係侾丂丄俀俁係俆侾丂丄俀俁係侾俆
丂丂俀俁侾係丂偺応崌丄丂俀俆俁侾係丂丄俀俁俆侾係丂丄俀俁侾俆係丂丄俀俁侾係俆
丂丂俀係侾俁丂偺応崌丄丂俀俆係侾俁丂丄俀係俆侾俁丂丄俀係侾俆俁丂丄俀係侾俁俆
丂丂俀侾係俁丂偺応崌丄丂俀俆侾係俁丂丄俀侾俆係俁丂丄俀侾係俆俁丂丄俀侾係俁俆
丂丂俀侾俁係丂偺応崌丄丂俀俆侾俁係丂丄俀侾俆俁係丂丄俀侾俁俆係丂丄俀侾俁係俆
丂傛偭偰丄媮傔傞応崌偺悢偼丄俀係捠傝偱偁傞丅丂丂乮廔乯
丂忋婰偺乮暿夝乯偼師偺傛偆偵夵椙偝傟傞丅
乮暿夝乯丂俀侾偺暲傃偱丄俁偺擖傟応強偼丄丂俀仜侾仜丂偺俀捠傝
丂偦偺侾捠傝丄椺偊偽丄俀俁侾 偵懳偟偰丄係偺擖傟応強偼丄俀仜俁仜侾仜丂偺俁捠傝
丂偦偺侾捠傝丄椺偊偽丄俀係俁侾丂偵懳偟偰丄俆偺擖傟応強偼丄俀仜係仜俁仜侾仜丂偺係捠傝
傛偭偰丄媮傔傞応崌偺悢偼丄丂俀亊俁亊係亖俀係乮捠傝乯
乮鶤乯丂俆俀侾偺暲傃偱丄俁偺擖傟応強偼丄丂俆俀仜侾仜丂偺俀捠傝
丂偦偺侾捠傝丄椺偊偽丄俆俀俁侾丂偵懳偟偰丄係偺擖傟応強偼丄俆俀仜俁仜侾仜丂偺俁捠傝
傛偭偰丄媮傔傞応崌偺悢偼丄丂俀亊俁亖俇乮捠傝乯
乮僄乯丂俆俀侾偺暲傃偱丄俁偺擖傟応強偼丄丂俆俀仜侾仜丂偺俀捠傝
丂偦偺侾捠傝丄椺偊偽丄俆俀俁侾 偵懳偟偰丄係偺擖傟応強偼丄俆俀仜俁仜侾仜丂偺俁捠傝
丂偦偺侾捠傝丄椺偊偽丄俆俀係俁侾丂偵懳偟偰丄俇偺擖傟応強偼丄俆仜俀仜係仜俁仜侾仜丂偺俆捠傝
傛偭偰丄媮傔傞応崌偺悢偼丄丂俀亊俁亊俆亖俁侽乮捠傝乯
乮俁乯丂俈俆係俀侾偺暲傃偱丄俁偺擖傟応強偼丄丂俈俆係俀仜侾仜丂偺俀捠傝
丂偦偺侾捠傝丄椺偊偽丄俈俆係俀俁侾 偵懳偟偰丄
丂丂俇偺擖傟応強偼丄俈俆仜係仜俀仜俁仜侾仜 偺俆捠傝
丂偦偺侾捠傝丄椺偊偽丄俈俆俇係俀俁侾丂偵懳偟偰丄
丂丂俉偺擖傟応強偼丄俈仜俆仜俇仜係仜俀仜俁仜侾仜丂偺俈捠傝
丂偦偺侾捠傝丄椺偊偽丄俈俉俆俇係俀俁侾丂偵懳偟偰丄
丂丂俋偺擖傟応強偼丄俈仜俉仜俆仜俇仜係仜俀仜俁仜侾仜丂偺俉捠傝
傛偭偰丄媮傔傞応崌偺悢偼丄丂俀亊俆亊俈亊俉亖俆俇侽乮捠傝乯丂丂乮廔乯
俁丏丂捈曽懱X傪俁偮偺暯柺 P丄Q丄R 偱愗抐偟偰丄偄偔偮偐偺棫懱偑偱偒傞丅偙偺偆偪偺侾偮傪
丂偲偭偰丄棫懱Y偲屇傇偙偲偵偡傞丅
丂丂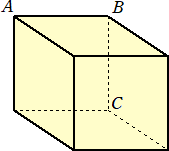
丂棫懱倄偺揥奐恾偼壓恾偺傛偆偵側傞偙偲偑暘偐偭偰偄傞丅偨偩偟丄曈(偁)丄曈(偄)偵偮偯偔柺
偑丄偦傟偧傟侾偮偢偮彂偐傟偰偄側偄丅傑偨丄捈曽懱X偺揰A丄B丄C偑丄棫懱Y偺揥奐恾偺揰
俙丄B丄C偵懳墳偡傞丅
丂丂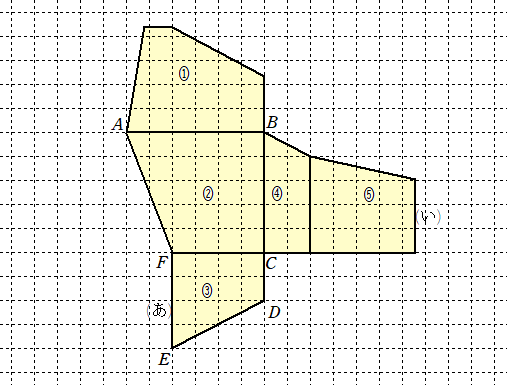
乮侾乯丂棫懱倄偺揥奐恾偺柺嘆乣嘍偺拞偱丄傕偲傕偲捈曽懱X偺柺偱偁偭偨傕偺傪偡傋偰摎偊傛丅
乮俀乯丂棫懱倄偺揥奐恾偵彂偐傟偨揰俢丄俤丄俥偵懳墳偡傞揰偼丄捈曽懱倃偺曈忋偵偁傞丅曈忋
丂偺挿偝偺斾偑側傞傋偔惓妋偵側傞傛偆偵拲懹偟偰丄揰俢丄俤丄俥偵懳墳偡傞揰傪丄捈曽懱倃偺
丂尒庢恾偵偐偒擖傟傛丅
乮俁乯丂暯柺俹偱捈曽懱X傪愗抐偟偨偲偒偺抐柺丄Q偱愗抐偟偨偲偒偺抐柺丄俼偱愗抐偟偨偲偒偺
丂抐柺偼丄偦傟偧傟偳偺傛偆側恾宍偵側傞偐丅師偺恾偺傛偆側偐偒曽偱丄捈曽懱X偺尒庢恾
丂偵侾偮偢偮彂偒擖傟傛丅
丂丂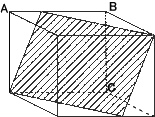
乮係乯丂棫懱倄偺揥奐恾偵丄(偁)丄(偄)偵偮偯偔柺傪丄側傞傋偔惓妋偵彂偒擖傟傛丅
乮俆乯丂揥奐恾偺傂偲栚惙傪侾們倣偲偡傞丅乮係乯偱彂偒擖傟偨柺偺偆偪丄(偄)偵偮偯偔傎偆偺柺愊傪
丂媮傔傛丅
乮夝乯乮侾乯丂捀揰俠偺廃傝偺俋侽亱偺娭學偐傜丄柧傜偐偵丄嘇丄嘊丄嘋
乮俀乯丂棫懱倄偺揥奐恾偐傜傕偲偺棫懱傪暅尦偟偰丄
丂丂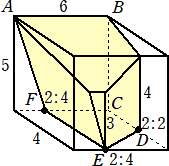
丂揰俢丄俤丄俥偵懳墳偡傞揰偼忋恾偺傛偆偵側傞丅
乮俁乯丂乮俀乯偺棫懱偐傜丄俁偮偺暯柺偱愗抐偟偨抐柺偼丄壓恾偺捠傝偲側傞丅
乮係乯丂乮俀乯偺棫懱偐傜丄(偁)丄(偄)偵偮偯偔柺傪丄彂偒擖傟傞偲丄
丂丂
乮俆乯丂(偄)偵偮偯偔恾宍偼捈妏嶰妏宍偱偁傞丅
丂丂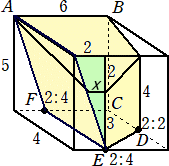
丂忋恾偐傜丄倶 偺抣偼丄丂俀 丗 倶亖俆 丗 俁丂偐傜丄丂倶亖侾丏俀
丂傛偭偰丄媮傔傞捈妏嶰妏宍偺柺愊偼丄丂侾丏俀亊俁亐俀亖侾丏俉乮們倣2乯丂丂乮廔乯
乮僐儊儞僩乯丂嬻娫攃埇偑抌偊傜傟偨栤戣偱偟偨丅
乮捛婰乯丂椷榓俇擭俀寧侾係擔晅偗
丂拀攇戝妛晬懏嬵応拞妛偺擖帋偑俀寧俁擔偵峴傢傟丄偄偔偮偐嫽枴偁傞栤戣偵挧愴偟偰傒
偨丅栤戣偼夵戣偝傟偰偄傑偡丅
[侾]丂惍悢俙偑偁傞丅俙偵懳偟偰丄惍悢俛丄俠丄俢傪師偺傛偆偵寛傔偰偄偔丅
亙寛傔曽亜丂俙傪俁俈偱妱偭偨偁傑傝偑俛丄俛傪侾俈偱妱偭偨偁傑傝偑俠丄俠傪俈偱妱偭偨偁傑傝
丂丂丂丂丂丂丂丂偑俢偱偁傞丅
丂師偺栤偄偵摎偊傛丅
乮侾乯丂俛亖俀俇丄俠亖俋丄俢亖俀偲側傞傛偆側俙偲偟偰峫偊傜傟傞悢偺偆偪丄嵟傕
丂丂彫偝偄傕偺偼俀俇偱偡偑丄俀斣栚偵彫偝偄傕偺偼壗偱偡偐丅
乮俀乯丂俢亖俀偲側傞傛偆側俙偲偟偰峫偊傜傟傞悢偺偆偪丄俀侽俀係埲壓偺傕偺偼慡晹偱壗屄偁傞偐丅
乮俁乯丂俛丄俠丄俢偑偡傋偰偪偑偆悢偲側傞傛偆側俙偲偟偰峫偊傜傟傞悢偺偆偪丄俀侽俀係埲壓偺傕偺
丂偼慡晹偱壗屄偁傞偐丅
乮夝乯乮侾乯丂戣堄傛傝丄俙亖俁俈俙乫亄俀俇丄俀俇亖侾俈丒侾亄俋丄俋亖俈丒侾亄俀丂側偺偱丄俀斣栚偵彫
丂偝偄傕偺偼丄俙乫亖侾偲偟偰丄丂俙亖俁俈亄俀俇亖俇俁
乮俀乯丂俢亖俀丂傛傝丄丂俙亖俁俈俙乫亄俛丄俛亖侾俈丒俛乫亄俠丄俠亖俈丒俠乫亄俀丂偵偍偄偰丄
丂侽亝俠亝侾俇丂傛傝丄丂侽亝俈丒俠乫亄俀亝侾俇丂偐傜丄丂俠乫亖侽丄侾丄俀
俠乫亖侽丂偺偲偒丄丂俠亖俀丂偱丄丂俛亖侾俈丒俛乫亄俀
丂偙偙偱丄丂侽亝俛亝俁俇丂傛傝丄丂侽亝侾俈丒俛乫亄俀亝俁俇丂偐傜丄丂俛乫亖侽丄侾丄俀
丂俛乫亖侽丂偺偲偒丄丂俛亖俀丂偱丄丂俙亖俁俈俙乫亄俀
丂俙亝俀侽俀係丂偐傜丄丂俁俈俙乫亄俀亝俀侽俀係丂側偺偱丄丂俙乫亖侽丄侾丄丒丒丒丄俆係
丂偡側傢偪丄丂俙亖俀丄俁俋丄丒丒丒丄俀侽侽侽丂偺俆俆屄偑奩摉偡傞丅
丂俛乫亖侾丂偺偲偒丄丂俛亖侾俋丂偱丄丂俙亖俁俈俙乫亄侾俋
丂俙亝俀侽俀係丂偐傜丄丂俁俈俙乫亄侾俋亝俀侽俀係丂側偺偱丄丂俙乫亖侽丄侾丄丒丒丒丄俆係
丂偡側傢偪丄丂俙亖侾俋丄俆俇丄丒丒丒丄俀侽侾俈丂偺俆俆屄偑奩摉偡傞丅
丂俛乫亖俀丂偺偲偒丄丂俛亖俁俇丂偱丄丂俙亖俁俈俙乫亄俁俇
丂俙亝俀侽俀係丂偐傜丄丂俁俈俙乫亄俁俇亝俀侽俀係丂側偺偱丄丂俙乫亖侽丄侾丄丒丒丒丄俆俁
丂偡側傢偪丄丂俙亖俁俇丄俈俁丄丒丒丒丄侾俋俋俈丂偺俆係屄偑奩摉偡傞丅
俠乫亖侾丂偺偲偒丄丂俠亖俋丂偱丄丂俛亖侾俈丒俛乫亄俋
丂偙偙偱丄丂侽亝俛亝俁俇丂傛傝丄丂侽亝侾俈丒俛乫亄俋亝俁俇丂偐傜丄丂俛乫亖侽丄侾
丂俛乫亖侽丂偺偲偒丄丂俛亖俋丂偱丄丂俙亖俁俈俙乫亄俋
丂俙亝俀侽俀係丂偐傜丄丂俁俈俙乫亄俋亝俀侽俀係丂側偺偱丄丂俙乫亖侽丄侾丄丒丒丒丄俆係
丂偡側傢偪丄丂俙亖俁俈丄係俇丄丒丒丒丄俀侽侽俈丂偺俆俆屄偑奩摉偡傞丅
丂俛乫亖侾丂偺偲偒丄丂俛亖俀俇丂偱丄丂俙亖俁俈俙乫亄俀俇
丂俙亝俀侽俀係丂偐傜丄丂俁俈俙乫亄俀俇亝俀侽俀係丂側偺偱丄丂俙乫亖侽丄侾丄丒丒丒丄俆係
丂偡側傢偪丄丂俙亖俀俇丄俇俁丄丒丒丒丄俀侽俀係丂偺俆俆屄偑奩摉偡傞丅
俠乫亖俀丂偺偲偒丄丂俠亖侾俇丂偱丄丂俛亖侾俈丒俛乫亄侾俇
丂偙偙偱丄丂侽亝俛亝俁俇丂傛傝丄丂侽亝侾俈丒俛乫亄侾俇亝俁俇丂偐傜丄丂俛乫亖侽丄侾
丂俛乫亖侽丂偺偲偒丄丂俛亖侾俇丂偱丄丂俙亖俁俈俙乫亄侾俇
丂俙亝俀侽俀係丂偐傜丄丂俁俈俙乫亄侾俇亝俀侽俀係丂側偺偱丄丂俙乫亖侽丄侾丄丒丒丒丄俆係
丂偡側傢偪丄丂俙亖侾俇丄俆俁丄丒丒丒丄俀侽侾係丂偺俆俆屄偑奩摉偡傞丅
丂俛乫亖侾丂偺偲偒丄丂俛亖俁俁丂偱丄丂俙亖俁俈俙乫亄俁俁
丂俙亝俀侽俀係丂偐傜丄丂俁俈俙乫亄俁俁亝俀侽俀係丂側偺偱丄丂俙乫亖侽丄侾丄丒丒丒丄俆俁
丂偡側傢偪丄丂俙亖俁俁丄俈侽丄丒丒丒丄侾俋俋係丂偺俆係屄偑奩摉偡傞丅
丂埲忋偐傜丄媮傔傞俙偼丄丂俆俆亄俆俆亄俆係亄俆俆亄俆俆亄俆俆亄俆係亖俁俉俁屄偁傞丅丂丂乮廔乯
乮暿夝乯丂忋婰偺乮夝乯傪惍棟偟偰偍偙偆丅
丂俠亖俈丒俠乫亄俀丂偐傜丄俠偺壜擻惈偼丄丂俠亖俀丄俋丄侾俇丂偺俁捠傝
丂俛亖侾俈丒俛乫亄俠丂偐傜丄俛偺壜擻惈偼丄
丂丂俛亖俀丄俋丄侾俇丄侾俋丄俀俇丄俁俁丄俁俇丂偺俈捠傝
丂傛偭偰丄俙亖俁俈俙乫亄俛丂偱丄俙亝俀侽俀係丂傪枮偨偡傕偺傪扵偡偲丄
丂[乮俀侽俀係亅俛乯/俁俈]亖俆係丄俆係丄俆係丄俆係丄俆係丄俆俁丄俆俁
側偺偱丄奩摉偡傞俙偼丄丂俆俆亊俆亄俆係亊俀亖俁俉俁乮屄乯丂丂乮廔乯
乮僐儊儞僩乯丂偩偄傇夝摎偑弅栺偱偒偨両
乮俁乯丂戣堄傛傝丄俙亖俁俈俙乫亄俛丄俛亖侾俈丒俛乫亄俠丄俠亖俈丒俠乫亄俢丂偵偍偄偰丄
丂侽亝俛亝俁俇丂丄侽亝俠亝侾俇丂丄侽亝俢亝俇丂偱偁傞丅
丂俁俇亝俛亝俁係丂偲偡傞偲丄俠亖俢丂偲側傝丄偙傟偼丄晄揔
丂俛亖俁俁丂偲偡傞偲丄俠亖侾俇丂丄俢亖俀丂偙傟偼丄揔
丂俛亖俁俀丂偲偡傞偲丄俠亖侾俆丂丄俢亖侾丂偙傟偼丄揔
丂俛亖俁侾丂偲偡傞偲丄俠亖侾係丂丄俢亖侽丂偙傟偼丄揔
丂俛亖俁侽丂偲偡傞偲丄俠亖侾俁丂丄俢亖俇丂偙傟偼丄揔
丂俛亖俀俋丂偲偡傞偲丄俠亖侾俀丂丄俢亖俆丂偙傟偼丄揔
丂俛亖俀俉丂偲偡傞偲丄俠亖侾侾丂丄俢亖係丂偙傟偼丄揔
丂俛亖俀俈丂偲偡傞偲丄俠亖侾侽丂丄俢亖俁丂偙傟偼丄揔
丂俛亖俀俇丂偲偡傞偲丄俠亖俋丂丄俢亖俀丂偙傟偼丄揔
丂俛亖俀俆丂偲偡傞偲丄俠亖俉丂丄俢亖侾丂偙傟偼丄揔
丂俛亖俀係丂偲偡傞偲丄俠亖俈丂丄俢亖侽丂偙傟偼丄揔
丂侾俈亝俛亝俀俁丂偲偡傞偲丄俠亖俢丂偲偁傝丄偙傟偼丄晄揔
丂侽亝俛亝侾俇丂偲偡傞偲丄俛亖俠丂偲側傝丄偙傟偼丄晄揔
丂埲忋偐傜丄奩摉偡傞俙偼丄
丂俙亖俁俈俙乫亄俛丂乮俛亖俀係丄俀俆丄俀俇丄俀俈丄俀俉丄俀俋丄俁侽丄俁侾丄俁俀丄俁俁乯
偙偺偲偒丄丂[乮俀侽俀係亅俛乯/俁俈]亖俆係丄俆係丄俆係丄俆俁丄俆俁丄俆俁丄俆俁丄俆俁丄俆俁丄俆俁丂側偺偱丄
奩摉偡傞俙偺屄悢偼丄丂俆俆亊俁亄俆係亊俈亖俆係俁乮屄乯
乮僐儊儞僩乯丂婥偑墦偔側傞傛偆側応崌暘偗偱偟偨偑丄懡彮夝摎傪弅栺偡傞偙偲偑偱偒傑偟偨両
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭俀寧侾俈擔晅偗乯
丂乮俁乯傕丄乮俀乯偺夵椙屻偺夝朄偲摨條偵偡傟偽丄偙傫側応崌暘偗偟側偔偰傕嵪傓偺偱偼側偄偐
偲巚偄傑偡丅
丂D 偑 C 偲摍偟偔側傞 C 偺斖埻偼 0亝C亝6 偱丄C 偼傕偲傕偲 0亝C亝16 偩偐傜丄D 偑 C 偲
堎側傞傛偆側斖埻偼 7亝C亝16
丂C 偑 B 偲摍偟偔側傞 B 偺斖埻偼 0亝B亝16 偱丄B 偼傕偲傕偲 0亝B亝36 偩偐傜丄D 偑 C 偲
堎側傞傛偆側斖埻偼 17亝B亝36丂偦偺偆偪丄7亝C亝16 偲側傞斖埻偼 24亝B亝33
丂埲壓丄忋婰夝摎偲摨偠丅
[俀]丂僒僀僐儘偼丄岦偐偄崌偆柺偺栚偺悢偺榓偑俈偵側偭偰偄傞丅偄偔偮偐偺僒僀僐儘傪丄偦偺
丂柺摨巑偑挌搙廳側傞傛偆偵揬傝崌傢偣偰偱偒偨棫懱偱丄廳側偭偰塀傟偨柺偺栚偺悢偺崌寁
丂傪乽僂儔偺榓乿丄塀傟偰偄側偄柺偺栚偺悢偺崌寁傪乽僆儌僥偺榓乿偲偄偆偙偲偵偡傞丅
乮侾乯丂俁屄偺僒僀僐儘傪壓恾偺傛偆偵揬傝崌傢偣傞丅
丂丂
丂乽僆儌僥偺榓乿偲偟偰峫偊傜傟傞傕偺偺偆偪丄傕偭偲傕戝偒偄悢偲傕偭偲傕彫偝偄悢傪偦傟偧傟
摎偊傛丅
乮俀乯丂俁屄偺僒僀僐儘傪壓恾偺傛偆偵揬傝崌傢偣傞丅
丂丂
丂偙偺偲偒丄乽僆儌僥偺榓乿偑乽僂儔偺榓乿偱傢傝愗傟傞偙偲偑偁傞丅偙偺傛偆側乽僆儌僥偺榓乿偲
偟偰丄峫偊傜傟傞傕偺傪偡傋偰摎偊傛丅
乮俁乯丂係屄偺僒僀僐儘傪壓恾偺傛偆偵揬傝崌傢偣傞丅
丂丂
丂偙偺偲偒丄乽僆儌僥偺榓乿偑乽僂儔偺榓乿偱傢傝愗傟傞偙偲偑偁傞丅偙偺傛偆側乽僆儌僥偺榓乿偲
偟偰丄峫偊傜傟傞傕偺傪偡傋偰摎偊傛丅
乮係乯丂係屄偺僒僀僐儘傪揬傝崌傢偣傞偲偒丄乽僆儌僥偺榓乿偲偟偰峫偊傜傟傞傕偺偺偆偪丄傕偭偲
丂傕戝偒偄悢偲傕偭偲傕彫偝偄悢傪偦傟偧傟摎偊傛丅
乮夝乯乮侾乯丂堦偮偺僒僀僐儘偺栚偺憤榓偼丄丂侾亄俀亄俁亄係亄俆亄俇亖俇亊俈亐俀亖俀侾
丂俁屄偺僒僀僐儘傪揬傝崌傢偣傞偲偒丄丂俀侾亊俁亅乽僂儔偺榓乿亖乽僆儌僥偺榓乿丂偑惉傝棫偮丅
丂偙偺偲偒丄丂乽僂儔偺榓乿偺壜擻惈偼丄丂俈亄俀丄俈亄俁丄丒丒丒丄俈亄侾俀丂偡側傢偪丄
丂俋丄侾侽丄丒丒丒丄侾俋丂偱偁傞丅傛偭偰丄乽僆儌僥偺榓乿丂偺壜擻惈偼丄丂俆係丄俆俁丄丒丒丒丄係係
丂傛偭偰丄傕偭偲傕戝偒偄悢偼丄俆係丂丄傕偭偲傕彫偝偄悢偼丄係係丂偱偁傞丅
乮俀乯丂俁屄偺僒僀僐儘偺揬傝崌傢偣傛傝丄丂俇俁亅乽僂儔偺榓乿亖乽僆儌僥偺榓乿丂偡側傢偪丄
丂俇俁亖乽僂儔偺榓乿亄乽僆儌僥偺榓乿丂偑惉傝棫偮偺偱丄
丂乽僆儌僥偺榓乿偑乽僂儔偺榓乿偱傢傝愗傟傞偲偒丄丂俇俁偼乽僂儔偺榓乿偱傢傝愗傟傞丅
丂乽僂儔偺榓乿偺壜擻惈偼丄丂俀亄俁丄丒丒丒丄侾俀亄侾侾丂偡側傢偪丄俆丄俇丄丒丒丒丄俀俁
丂偙偺拞偱俇俁偺栺悢偼丄丂俀侾丄俋丄俈丂側偺偱丄乽僆儌僥偺榓乿亖俇俁亅乽僂儔偺榓乿丂傛傝丄
丂乽僆儌僥偺榓乿偲偟偰峫偊傜傟傞傕偺偼丄丂係俀丄俆係丄俆俇丂偱偁傞丅
乮俁乯丂係屄偺僒僀僐儘偺揬傝崌傢偣傛傝丄丂俉係亅乽僂儔偺榓乿亖乽僆儌僥偺榓乿丂偡側傢偪丄
丂俉係亖乽僂儔偺榓乿亄乽僆儌僥偺榓乿丂偑惉傝棫偮偺偱丄
丂乽僆儌僥偺榓乿偑乽僂儔偺榓乿偱傢傝愗傟傞偲偒丄丂俉係偼乽僂儔偺榓乿偱傢傝愗傟傞丅
丂乽僂儔偺榓乿偺壜擻惈偼丄丂俀亄俈亄俁丄丒丒丒丄侾俀亄俈亄侾侾丂偡側傢偪丄侾俀丄侾係丄丒丒丒丄俁侽
丂偙偺拞偱俉係亖俀2丒俁丒俈 偺栺悢偼丄丂侾俀丄侾係丄俀侾丄俀俉丂側偺偱丄
丂乽僆儌僥偺榓乿亖俉係亅乽僂儔偺榓乿丂傛傝丄
丂乽僆儌僥偺榓乿偲偟偰峫偊傜傟傞傕偺偼丄丂俈俀丄俈侽丄俇俁丄俆俇丂偱偁傞丅
乮係乯丂係屄偺僒僀僐儘偺揬傝崌傢偣傛傝丄丂俉係亅乽僂儔偺榓乿亖乽僆儌僥偺榓乿丂偑惉傝棫偮丅
丂乽僂儔偺榓乿偺嵟戝抣偼丄俆偲俇偱係柺偑揬傝崌傢偝傟傞偲偒偱丄丂侾侾亊係亖係係
丂嵟彫抣偼丄侾偲侾丄俀偲侾丄俀偲侾丂偱俁柺偑揬傝崌傢偝傟傞偲偒偱丄俀亄俁亄俁亖俉
側偺偱丄乽僆儌僥偺榓乿偲偟偰峫偊傜傟傞嵟彫抣偼丄俉係亅係係亖係侽
丂乽僆儌僥偺榓乿偲偟偰峫偊傜傟傞嵟戝抣偼丄俉係亅俉亖俈俇丂丂乮廔乯
[俁]丂堦曈偺挿偝偑侾俀cm偺惓榋妏宍ABCDEF偑偁傞丅捈慄AD忋偵揰G丄捈慄CF忋偵揰H
丂丂偑偁傞丅仮AGF偺妏G丄仮CHD偺妏H偼丄偳偪傜傕捈妏偱偁傞丅
丂揰P偼捀揰A傪弌敪偟丄惓榋妏宍偺曈忋傪枅昩侾cm偺懍偝偱 A仺B仺C仺D仺E仺F仺A 偺
弴偵堦廃偟丄摦偒巒傔偰偐傜俈俀昩屻偵A偱巭傑傞丅
丂丂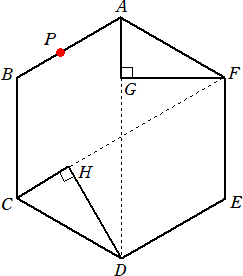
丂P偲G丄G偲H丄H偲P傪傑偭偡偖側慄偱寢傫偱嶌偭偨恾宍PGH傪峫偊傞丅師偺栤偄偵摎偊傛丅
乮侾乯丂恾宍PGH偑嶰妏宍偵側傜側偄偺偼丄P偑摦偒巒傔偰偐傜壗昩屻偱偡偐丅
乮俀乯丂恾宍PGH偑嶰妏宍偵側傝丄仮PGH偺柺愊偑仮AGF偺柺愊偲摍偟偔側傞偺偼丄P偑摦偒
丂巒傔偰偐傜壗昩屻偱偡偐丅
乮俁乯丂P偲B丄B偲H丄H偲P傪傑偭偡偖側慄偱寢傫偱嶌偭偨恾宍PBH傪峫偊傞丅偨偩偟丄P偑B偵廳
丂側傞応崌偼峫偊側偄傕偺偲偡傞丅
丂恾宍PGH丄恾宍PBH偑偳偪傜傕嶰妏宍偵側傝丄仮PGH偺柺愊偑仮PBH偺柺愊偲摍偟偔側傞
丂偺偼丄P偑摥偒巒傔偰偐傜壗昩屻偱偡偐丅
乮夝乯乮侾乯丂恾宍PGH偑嶰妏宍偵側傜側偄偺偼丄揰俹偑壓恾偺埵抲偵偁傞偲偒偱偁傞丅
丂丂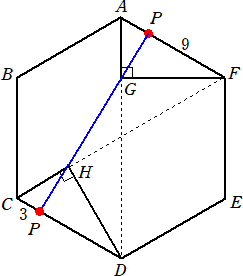
丂傛偭偰丄丂侾俀亊俀亄俁亖俀俈丂丄侾俀亊俆亄俋亖俇俋乮昩屻乯丂偱偁傞丅
乮俀乯丂仮PGH偺柺愊偑仮AGF偺柺愊偲摍偟偔側傞偺偼丄揰俹偑壓恾偺埵抲偵偁傞偲偒偱偁傞丅
丂丂
丂傛偭偰丄俇丄侾俀亄俇亖侾俉丄侾俀亊俀亄俋亖俁俁丄侾俀亊俆亄俁亖俇俁乮昩屻乯丂偱偁傞丅
乮俁乯丂仮PGH偺柺愊偑仮PBH偺柺愊偲摍偟偔側傞偺偼丄揰俹偑壓恾偺埵抲偵偁傞偲偒偱偁傞丅
丂丂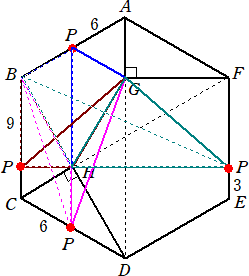
丂傛偭偰丄俇丄侾俀亄俋亖俀侾丄侾俀亊俀亄俇亖俁侽丄侾俀亊係亄俁亖俆侾乮昩屻乯丂偱偁傞丅丂丂乮廔乯
乮僐儊儞僩乯丂摍愊曄宍偑抌偊傜傟傑偟偨両
[係]丂堦曈偺挿偝偑侾侽cm偺棫曽懱偺柺偳偆偟傪偪傚偆偳廳側傞傛偆偵慻傒崌傢偣偰偮偔偭偨
丂僽儘僢僋A丄B丄C偑偁傞丅僽儘僢僋A偼棫曽懱俇屄丄僽儘僢僋B偼棫曽懱俀屄丄僽儘僢僋C偼棫
丂曽懱俁屄傪慻傒崌傢偣偨傕偺偱偁傞丅
丂僽儘僢僋俙丄僽儘僢僋俛丄僽儘僢僋俠傪丄棫曽懱偺柺偳偆偟偑偪傚偆偳廳側傞傛偆偵丄偝傜偵慻傒
崌傢偣傞偙偲傪峫偊傞丅偨偩偟丄暆丄墱峴偒丄崅偝偼偳傟傕俁侽cm埲壓偲側傞傛偆偵偡傞丅
丂堦曈偺挿偝偑俁侽cm偺棫曽懱偺宍偺悈偦偆偑偁傞丅悈暯偵抲偐傟偨嬻偺悈偦偆偵僽儘僢僋
傪抲偒丄侾俀侽侽侽們倣3偺悈傪擖傟偰悈柺偺崅偝傪挷傋傞丅師偺栤偄偵摎偊傛丅
乮侾乯丂僽儘僢僋A傪侾屄丄悈偦偆偵抲偄偨偲偙傠丄壓恾偺傛偆偵側偭偨丅悈傪擖傟偨偁偲偺悈柺
丂丂偺崅偝偼丄悈偦偆偺彴偐傜壗cm偵側傞偐丅
丂丂
乮俀乯丂僽儘僢僋A偲僽儘僢僋B傪侾屄偢偮慻傒崌傢偣偨傕偺傪悈偦偆偵抲偄偨偲偙傠丄恀忋偐傜
丂尒偨傜丄壓恾偺傛偆偵側偭偨丅偨偩偟丄僽儘僢僋A偺埵抲傗岦偒偼乮侾乯偲曄傢傜側偄傕偺偲偡
丂傞丅悈傪擖傟偨偁偲偺悈柺偺崅偝偼丄悈偦偆偺彴偐傜壗cm偵側傞丄峫偊傜傟傞傕偺傪偡傋
丂偰摎偊傛丅
丂丂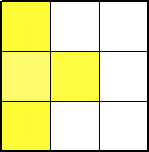
乮俁乯丂僽儘僢僋A丄僽儘僢僋B丄僽儘僢僋C傪侾屄偢偮慻傒崌傢偣偨傕偺傪悈偦偆偵抲偄偨偲偙傠丄
丂恀忋偐傜尒偨傜壓恾偺傛偆偵側偭偨丅偨偩偟丄僽儘僣僋A偺埵抲傗岦偒偼乮侾乯偲曄傢傜側偄
丂傕偺偲偡傞丅悈傪擖傟偨偁偲偺悈柺偺崅偝偼丄悈偦偆偺彴偐傜壗cm偵側傞偐丄峫偊傜傟傞
丂傕偺傪偡傋偰摎偊傛丅
丂丂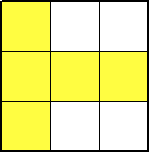
乮夝乯乮侾乯丂堦曈偺挿偝偑侾侽cm偺棫曽懱偺懱愊偼丄侾侽侽侽們倣3丂偱偁傞丅
丂僽儘僢僋俙傪彍偄偨嬻偒僗儁乕僗偼丄侾抜栚丒丒丒棫曽懱俇屄暘丄俀抜栚丒丒丒棫曽懱俈屄暘
丂偟偨偑偭偰丄悈柺偺崅偝偼丄侾抜栚偲俀抜栚偺娫偵偁傞丅
丂傛偭偰丄悈柺偺崅偝偼丄丂侾侽亄乮侾俀侽侽侽亅俇侽侽侽乯亐俈侽侽亖侾侽亄俇侽/俈亖侾俁侽/俈乮們倣乯
乮俀乯丂峫偊傜傟傞応崌偼丄師偺俁捠傝偱偁傞丅
乮傾乯丂丂僽儘僢僋俙丄俛傪彍偄偨嬻偒僗儁乕僗偼丄
丂侾抜栚丒丒丒棫曽懱俆屄暘丄俀抜栚丒丒丒棫曽懱俇屄暘丄俁抜栚丒丒丒棫曽懱俉屄暘
丂偟偨偑偭偰丄悈柺偺崅偝偼丄俀抜栚偲俁抜栚偺娫偵偁傞丅
丂傛偭偰丄悈柺偺崅偝偼丄丂俀侽亄乮侾俀侽侽侽亅侾侾侽侽侽乯亐俉侽侽亖俀侽亄俆/係亖俉俆/係乮們倣乯
乮僀乯丂丂僽儘僢僋俙丄俛傪彍偄偨嬻偒僗儁乕僗偼丄
丂侾抜栚丒丒丒棫曽懱俇屄暘丄俀抜栚丒丒丒棫曽懱俇屄暘
丂偟偨偑偭偰丄悈柺偺崅偝偼丄俀抜栚偺崅偝偵摍偟偄偺偱丄悈柺偺崅偝偼丄丂俀侽乮們倣乯
乮僂乯丂丂僽儘僢僋俙丄俛傪彍偄偨嬻偒僗儁乕僗偼丄
丂侾抜栚丒丒丒棫曽懱俇屄暘丄俀抜栚丒丒丒棫曽懱俈屄暘
丂偟偨偑偭偰丄悈柺偺崅偝偼丄侾抜栚偲俀抜栚偺娫偵偁傞丅
丂傛偭偰丄悈柺偺崅偝偼丄丂侾侽亄乮侾俀侽侽侽亅俇侽侽侽乯亐俈侽侽亖侾侽亄俇侽/俈亖侾俁侽/俈乮們倣乯
乮俁乯丂峫偊傜傟傞応崌偼丄師偺係捠傝偱偁傞丅
乮傾乯丂丂僽儘僢僋俙丄俛丄俠傪彍偄偨嬻偒僗儁乕僗偼丄
丂侾抜栚丒丒丒棫曽懱係屄暘丄俀抜栚丒丒丒棫曽懱俆屄暘丄俁抜栚丒丒丒棫曽懱俈屄暘
丂偟偨偑偭偰丄悈柺偺崅偝偼丄俀抜栚偲俁抜栚偺娫偵偁傞丅
丂傛偭偰丄悈柺偺崅偝偼丄丂俀侽亄乮侾俀侽侽侽亅俋侽侽侽乯亐俈侽侽亖俀侽亄俁侽/俈亖侾俈侽/俈乮們倣乯
乮僀乯丂丂僽儘僢僋俙丄俛丄俠傪彍偄偨嬻偒僗儁乕僗偼丄
丂侾抜栚丒丒丒棫曽懱俆屄暘丄俀抜栚丒丒丒棫曽懱俆屄暘丄俁抜栚丒丒丒棫曽懱俇屄暘
丂偟偨偑偭偰丄悈柺偺崅偝偼丄俀抜栚偲俁抜栚偺娫偵偁傞丅
丂傛偭偰丄悈柺偺崅偝偼丄丂俀侽亄乮侾俀侽侽侽亅侾侽侽侽侽乯亐俇侽侽亖俀侽亄侾侽/俁亖俈侽/俁乮們倣乯
乮僂乯丂丂僽儘僢僋俙丄俛丄俠傪彍偄偨嬻偒僗儁乕僗偼丄
丂侾抜栚丒丒丒棫曽懱俆屄暘丄俀抜栚丒丒丒棫曽懱俇屄暘丄俁抜栚丒丒丒棫曽懱俆屄暘
丂偟偨偑偭偰丄悈柺偺崅偝偼丄俀抜栚偲俁抜栚偺娫偵偁傞丅
丂傛偭偰丄悈柺偺崅偝偼丄丂俀侽亄乮侾俀侽侽侽亅侾侾侽侽侽乯亐俆侽侽亖俀俀乮們倣乯
乮僄乯丂丂僽儘僢僋俙丄俛丄俠傪彍偄偨嬻偒僗儁乕僗偼丄
丂侾抜栚丒丒丒棫曽懱俇屄暘丄俀抜栚丒丒丒棫曽懱俇屄暘
丂偟偨偑偭偰丄悈柺偺崅偝偼丄俀抜栚偺崅偝偵摍偟偄偺偱丄悈柺偺崅偝偼丄俀侽乮們倣乯丂丂乮廔乯
乮僐儊儞僩乯丂廫暘妝偟傔偨栤戣偱偡偑丄帋尡帪娫撪偱夝偒偒傞帺怣偼慡偔偁傝傑偣傫偹両
丂丂埲壓丄岺帠拞両


 丂丂丂佢俙俷俛亖150亱偐傜丄
丂丂丂佢俙俷俛亖150亱偐傜丄




 丂丂乮鶣乯丂傾亄働亄僆亖俀係侾 偲側傞惍悢偼乮丂丂乯偱偡丅
丂丂乮鶣乯丂傾亄働亄僆亖俀係侾 偲側傞惍悢偼乮丂丂乯偱偡丅

































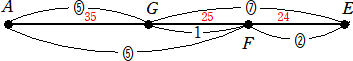











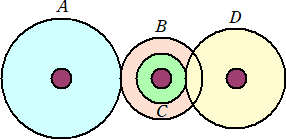



























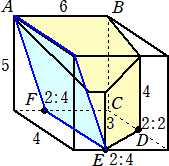 丂丂
丂丂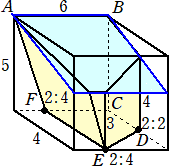 丂丂
丂丂