約数の積　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　戻る

　自然数 ６ の約数は、　１　、　２　、　３　、　６　　の４個ある。この約数の総和を求める
と、１２で、これは、もとの数の２倍に等しい。このような着眼が、完全数の話題であった。
（→　参考　：　「完全数」、「図形の完全数？」）

　これに対して、約数の全ての積を考えたら、どんな性質が成り立つのか？この問いかけ
を、当ＨＰがいつもお世話になっている加俊さんが考えられた。

　当ＨＰの掲示板「出会いの泉」に、４月１日付けで、加俊さんから、数論における一つの
面白い性質を発見した旨の報告があった。

　この報告に対して、当ＨＰがいつもお世話になっている、らすかるさん、ｚｋ４３さんから証
明を与えていただいた。このページでは、これらを整理した形でまとめていこうと思う。

　２以上の自然数 ｎ に対し、その正の約数を全て掛け合わせたものを　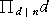　と表す。

例　２の約数は、１と２なので、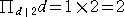　

　　以下同様にして、

　　　　　　、　　、　　、

　　　　　

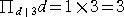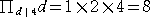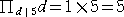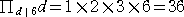
　と求められる。

　　　このとき、　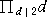 ≡ １　（ｍｏｄ　１）　・・・　本来は、０ であるが、便宜上 １ としておく。

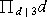　　　　　　　　　　 ≡ １　（ｍｏｄ　２）

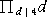　　　　　　　　　　 ≡ ２　（ｍｏｄ　３）　・・・　２ は、４ の平方根の．．．予感？

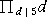　　　　　　　　　　 ≡ １　（ｍｏｄ　４）

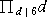　　　　　　　　　　 ≡ １　（ｍｏｄ　５）

　である。　加俊さんは、これらの計算から、次の性質を証明されたとのことである。

　　　　　　ｎ が平方数のとき、　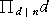 ≡ 　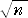（ｍｏｄ　ｎ−１）

　　　　　　ｎ が平方数でないとき、　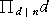 ≡ １　（ｍｏｄ　ｎ−１）

　このことから、

　　　　　　任意の非負整数 ａ に対して、ある自然数 ｎ が存在して、

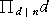　　　　　　　　　　　　 ≡ ａ　（ｍｏｄ　ｎ−１）

　　　　　で、これを満たす ｎ は、 a ＝ １ を除き、ただ一通りに定まる。

　これを証明するには、次の定理が本質的な役割を果たす。

定　理　　自然数 ｎ の約数（ １ と ｎ を含む）の個数を、τ（ｎ） とすると、

　　　　　　　　　　

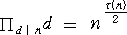
　　　　　が成り立つ。

　この定理は、よく知られていて、

　　　高木貞治　著　　初等整数論講義　　（岩波書店）
　　　北村泰一　著　　数論入門　　（槙書店）

などに、定理や問題として提示されている。

（証明）　ｎ の約数の一つを、ｄ とすると、　ｄ×ｄ’＝ｎ　となる ｄ’が存在する。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（この ｄ、ｄ’を互いに余約数という。）
　　　　このとき、明らかに、
　　　　　　　　　　　　　　　　　　

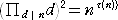
　　　が成り立つので、定理は成り立つ。　（証終）

　また、自然数 ｋ に対して、　ｎｋ−１＝（ｎ−１）（ｎｋ−1＋ｎｋ−2＋・・・＋ｎ＋１）　と因数分

解できるので、　　ｎｋ ≡ １　（ｍｏｄ　ｎ−１）　が成り立つ。

　これらを利用して、加俊さんの導かれた事実が容易に証明される。

（証明）　ｎ が平方数のとき、　τ（ｎ） は奇数なので、

　　　　

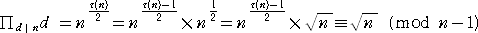
　　　　　ｎ が平方数でないとき、　τ（ｎ） は偶数なので、

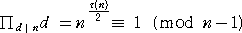　　　　　　（証終）

(コメント）　加俊さんが導かれたことは、

　　　　　　　　　　　

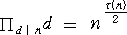
　　　　という事実を、さらに詳しく計算したということでしょうか。「ｍｏｄ　ｎ−１」という発想
　　　　が素晴らしいですね！上記をまとめるにあたり、加俊さん、らすかるさん、ｚｋ４３さん
　　　　のお助けをお借りしました。ここに感謝いたします。

（追記）　平成２０年４月５日付け

　完全数を意識して、ｚｋ４３さんは、

　　自分自身を除く約数の積が自分自身に等しいものはどんなものか？

ということを考えてみたという。（当ＨＰ掲示板「出会いの泉」　４月４日付け）

　ｚｋ４３さんの計算によれば、そのような性質を持つ数 ｎ の約数は、

　　　　　　　　１　、　ｄ　、　ｎ/ｄ　、　ｎ

の４個の場合に限るという。したがって、そのような数 ｎ は、

　　　　　　　　ｐｑ　　または　　ｐ3

と書けることになる。ただし、ｐ、ｑ は異なる素数とする。

　よって、条件を満たす自然数 ｎ は、無数に存在する。

　そこで、ｚｋ４３さんからの問題：

　　　このような数の逆数和は発散するか？収束するか？

　この問題に対して、らすかるさんが証明を与えられた。（平成２０年４月５日付け）

（証明）
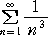　　　 　 　は収束するので、明らかに、 　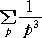 　も収束する。
　　　しかるに、 　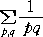 　について、ｐ＝２ と固定した部分の和 　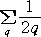 　について、
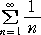　　　　 　が発散するのと同様に、発散する。
　　　したがって、 　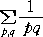 　は発散する。

　以上から、上記の性質を満たす数の逆数和は発散する。　（証終）

（コメント）　当初、「収束かな？」と思いきや、らすかるさんの証明を見ると、本当に自然な
　　　　　　証明で、思わず「ガッテン！」してしまいました。らすかるさんに感謝いたします。

　　　　　　　なお、出題者のｚｋ４３さんの当初想定した解答は、

　　　　　　　　　　

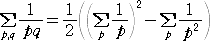
　　　　　　を利用するものだそうで、右辺の級数の形から発散が示されるとのことである。

（追記）　平成２０年４月１１日付け

　　加俊さんからの情報によれば、積版の完全数を積完全というらしい。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（正式かどうかは不明とのこと）

（追記）　平成２０年６月１５日付け

　ｚｋ４３ さんからの問題 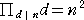： を満たす自然数 ｎ の逆数和は発散する

に関連して、加俊さんは、次の事実を示された。（当ＨＰ掲示板：平成２０年６月８日付け）

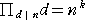　　 を満たす自然数 ｎ の逆数和は発散する

　ただし、 ｋ は ２ 以上の自然数とする。

（このような自然数 ｎ を、ｋ次の積完全と呼ぶことにする。）

（証明）　条件より、　τ（ｎ）＝２ｋ　となる。したがって、そのような数 ｎ の一つとして、

　　　　ｐｋ-1ｑ　（ｐ、ｑ は異なる素数） の形のものが存在する。

　　　このとき、 ｐ＝２ と固定した部分の和 　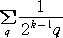 　は発散する。

　よって、上記の性質を満たす数の逆数和は発散する。　（証終）

　加俊さんは、「どんな ｋ次の積完全でも発散するという点が興味深い」と述べられている。
確かに、 　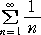 　は発散するという性質を持っているので、問題の級数も発散することは
予想されるが、発散するほど条件を満たす自然数が無数にあるということなんでしょうね！

　さらに、加俊さんは、次のような問題を提示された。

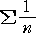　 　において、ｎ の値を順に、　１、２、３、・・・　と変化させれば、発散するが、

ｎ の値を順に、　１、２、４、８、１６、・・・　（初項 １ 公比 ２ の等比数列）と変化させれば、

和 ２ に収束する。そこで、

　自然数 ｎ の値を順に、どのような頻度で選んだときに、収束・発散の分かれ目が
見いだされるのだろうか？

　初項 １ 公比 ２ の等比数列は、あまりに「まばら」過ぎるので収束なんだろうが、ちょっと
油断して、自然数 ｎ の取り得る値として素数全体としてしまうと途端に発散してしまう。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（１７３７年　オイラー）

　自然数 ｎ の取り得る値として平方数全体とすると、この場合は収束する。ということは、
平方数の分布の仕方は、素数よりも「まばら」だということですね！

　この話題について、らすかるさんから、６月９日付けで

　　素数なら発散で、双子素数なら収束なので、その間ですね。

とご教示いただきました。らすかるさんに感謝いたします。

　双子素数とは、差が２の２つの素数の組のことで、たとえば、

　　３ と ５　、５ と ７ 、１１ と １３　、１７ と １９　、２９ と ３１　、４１ と ４３　、５９ と ６１　、

　７１ と ７３　、１０１ と １０３　、１０７ と １０９　、１３７ と １３９　、１４９ と １５１　、・・・

などである。

　「双子素数は無限個あるだろう」と予想されているが、まだ証明されていないとか？

　　（追記）　平成２５年８月９日付け

　　　　長らく未解決だったこの問題も、２０１３年５月にアメリカのニューハンプシャー大学の
　　　イータン・チャン氏により突破口が開かれた。すなわち、

　　　　　次の素数までの間隔が７０００万未満のペアなら無限にある

　　　ということが証明された。この７０００万という数字はかなり余裕をみて計算した結果と
　　　のことで、その後世界中の数学者が参戦し、７月には「約５０００」まで間隔が縮められ
　　　たらしい。

　　　　この間隔が「２」まで引き下げられれば、双子素数の予想は証明されるのだが、今は
　　　まだ無理のようだ。

　　　（参考文献：平成２５年８月５日付け　朝日新聞「科学」）


　ただ、驚くべきことに、双子素数の逆数和

　　　　　　　

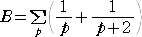
が収束することは、１９１９年にオランダの数学者のブルン（Ｂｒｕｎ）により証明されている。

　２００５年現在で、その和は、

　　　　　　　　１．９０２１６０５８３１０４・・・　　（この数値は、Ｓｅｂａｈ（２００２）による）

となることが知られている。

　多分、加俊さんが考えられたことは、数学の論文が書けるほどの難問ですね！