・　図形の完全数？　　　　 　　　　　　　　　　　　Ｓ．Ｈ氏

　ある数の約数（但し、自分自身は除く）の総和がある数自身に等しいとき、その数のこと
を、完全数という。完全数で一番有名な数は、６ である。

　実際に、６ の約数は、１、２、３ なので、１＋２＋３＝６ が成り立っている。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（→参考：完全数）

　このことと同様のことが正多角形においても起こるということを最近知ることができた。

　正多角形において、その頂点を結んでできる図形が正多角形のとき、その図形は元の
図形の「約数」と考える。

例　正６角形において、頂点を一つおきに結んでできる図形は正三角形で、正６角形の
　　「約数」となる。自分自身も「約数」で、約数は全部で、３個ある。

　正Ｎ角形において、その約数の総数が、Ｎ に等しいとき、正Ｎ角形のことを、「図形の
完全数」ということにしよう。

例　正６角形は、「図形の完全数」ではない。

例　正２４角形は、「図形の完全数」である。

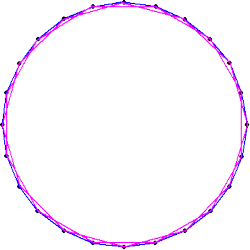
　正２４角形を、図形描画ソフトに描いてもらうと、ほぼ「円」に近い！

　　　　　　　　　

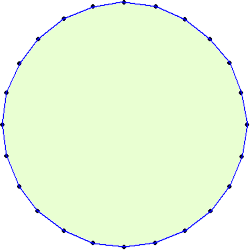
正３角形は、下図のように、８個ある。		正４角形は、下図のように、６個ある。
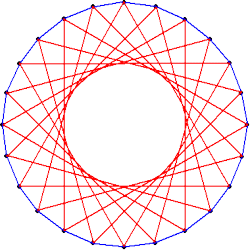
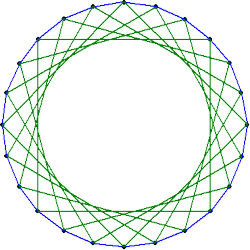
正６角形は、下図のように、４個ある。		正８角形は、下図のように、３個ある。
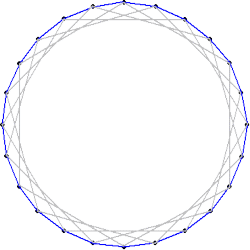
正１２角形は、下図のように、２個ある。

　以上から、「約数」の総数は、自分自身も含めて、　８＋６＋４＋３＋２＋１＝２４　で、
Ｎ＝２４　と一致する。したがって、正２４角形は、「図形の完全数」である。


　上記では図形を実際に描いて求めたが、直接計算によっても求めることができる。

　Ｎ＝２４　の約数は、　１、２、３、４、６、８、１２、２４　であるが、正 ｎ 角形において、ｎ≧３
なので、１ と ２ は除外して考える。
このとき、　正３角形の個数は、　２４÷３＝８（個）
　 　　　　　　正４角形の個数は、　２４÷４＝６（個）
　 　　　　　　正６角形の個数は、　２４÷６＝４（個）
　 　　　　　　正８角形の個数は、　２４÷８＝３（個）
　 　　　　　　正１２角形の個数は、　２４÷１２＝２（個）
と簡単に求められる。

　正Ｎ角形の「約数」の総数は、

　　　　　　Ｎが奇数のとき、　（Ｎの約数の総和）−Ｎ

　 　　　　Ｎが偶数のとき、　（Ｎの約数の総和）−（3/2）Ｎ

で求められる。

例　Ｎ＝２４＝２³・３　のとき、　Ｎ の約数の総和は、

　　　　　　（１＋２＋２²＋２³）（１＋３）＝１５×４＝６０

　　したがって、　正２４角形の「約数」の総数は、　６０−（3/2）・２４＝６０−３６＝２４


（コメント）　正２４角形以外に「図形の完全数」は存在するのだろうか？ちょっとプログラム
　　　　　　を組んで計算を試みたが発見することができなかった。数の完全数と同様に開
　　　　　　放型の問題であるので少し発見が難しい。新しい「図形の完全数」を発見された
　　　　　　方、是非こちらまでご教示ください。

（追記）　平成１８年４月１７日当ＨＰがいつもお世話になっているらすかるさんから、第２、
　　　　　第３の「図形の完全数」を発見した旨メールをいただいた。

　　Ｎ＝２４　以外の「図形の完全数」

　　　　　９１９６３６４８＝２⁸×７×１９×３７×７３

　　　　　１０２００２３６０３２＝２¹⁴×７×１９×３１×１５１


　　　この ９１９６３６４８ の全ての約数の和を計算してみると、

　　　　　（２⁹−１）（１＋７）（１＋１９）（１＋３７）（１＋７３）＝２２９９０９１２０

　　なので、これを元の数９１９６３６４８ で割ってみると、

　　　　　２２９９０９１２０÷９１９６３６４８＝２．５

　　となる。ちなみに、　２４＝２³・３ についても計算してみると、

　　　　　全ての約数の和＝（２⁴−１）（１＋３）＝６０

　　　より、　　６０÷２４＝２．５　で、９１９６３６４８ の場合と同じ値になっている。

　このような性質を持つ数同士を、Ｆｒｉｅｎｄｌｙ　Ｐａｉｒ と言うらしい。

（コメント）　最近映画でも話題になった「友愛数」のような雰囲気で、大変面白い性質です
　　　　　　ね！らすかるさんの計算結果にはいつも感服しております。らすかるさんに感謝
　　　　　　いたします。

（追々記）　平成１８年４月２１日当ＨＰがいつもお世話になっているらすかるさんから、最終
　　　　　　報告という形で「図形の完全数」についてのメールをいただいた。

　出来るだけ原文に近い形で以下に整理したいと思う。（私の誤解が入るといけないので）

　一般に信じられている“予想”や調査などによる数々の状況証拠からの“予想”であるが、

　　図形の完全数は、 ２４　、９１９６３６４８　、１０２００２３６０３２　の3つしかない

というのが結論である。

　以下、次の(一般に使用されている)用語を使用することにする。

　　　　σ（ｎ）： ｎ の約数の総和　　　σ（ｎ）/ｎ＝ｋ である数： ｋ 倍完全数

　完全数については多くの人の研究があるが、いろいろな予想の証明は難しいらしく、ちゃ
んと証明されていない予想が数多くある。その中で、

　　「奇数の完全数は存在しない」　　　「３倍完全数は６個だけである」

という予想をとりあえず正しいものと仮定する。

　図形の完全数は、ｎ が奇数の場合は、

　　　　（ ｎ の約数の総和）− ｎ ＝ ｎ

から、　σ（ｎ）/ｎ＝２　で、(２倍)完全数を求めることに等しく、偶数の場合は、

　　　　（ ｎ の約数の総和）−（3/2）ｎ ＝ ｎ

から、　σ（ｎ）/ｎ＝５/２　で、(２．５倍)完全数を求めることに等しいが、まず奇数の完全数
は存在しないので、奇数は除外して考えることにする。

　偶数の２．５倍完全数 ｎ が素因数５を持たない場合、σ(５ｎ)＝（１＋５）σ(ｎ)＝６σ(ｎ)　が
成り立つので、
　　　　　σ（５ｎ）/（５ｎ）＝６σ（ｎ）/（５ｎ）＝（６/５）σ（ｎ）/ｎ＝（６/５）（５/２）＝３

となり、５ｎは、３倍完全数となる。このことから、素因数５を１個だけ含むような３倍完全数
の １/５ 倍の数が、２．５倍完全数となる。

３倍完全数は、以下の６個である。

　１２０　（＝２³×３×５）　、６７２　（＝２⁵×３×７）　、５２３７７６　（＝２⁹×３×１１×３１）

　４５９８１８２４０　（＝２⁸×５×７×１９×３７×７３）

　１４７６３０４８９６　（＝２¹³×３×１１×４３×１２７）

　５１００１１８０１６０　（＝２¹⁴×５×７×１９×３１×１５１）


　この中で素因数５を１個だけ含むものは、　１２０、４５９８１８２４０、５１００１１８０１６０　の
３個であるが、これをそれぞれ １/５ 倍すると、

　　　２４　、９１９６３６４８　、１０２００２３６０３２

となり、ちょうど検索で見つけた３個の２．５倍完全数となる。

　これにより、素因数５を持たない２．５倍完全数は上記の３個だけということになる。

　したがって、もし上記の他に２．５倍完全数があるとすれば、それは５の倍数となる。

　これをさらに場合分けすると、検索量を大幅に減らすことが出来る。ｎ が２．５倍完全数な
らば、 ２σ(ｎ)＝５ｎ ということを考慮して素因数で場合分けをする。

　ここで、ｎ の素因数に５を持てば、σ(ｎ)は、６で割り切れ、ｎ は１２で割り切れる。すなわち
ｎ は、３で必ず割り切れることになり、ｎ は素因数として、３ を必ず含む。このことに注意して
場合分けを行う。

　ｎ の素因数に、３ と ５ を１個ずつ含むとき・・・　σ(ｎ)が、(１＋３)(１＋５)で割り切れるので、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　２σ(ｎ)は、２×４×６＝４８ で割り切れ、よっ
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　て、ｎ も４８で割り切れる。ｎ は５でも割り切
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　れるので、ｎ は、２４０の倍数となる。

　ｎ の素因数に、３ を２個、５ を１個含むとき・・・　σ(ｎ)が、(１＋３＋３²)(１＋５)で割り切れる
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ので、２σ(ｎ)は、２×１３×６＝１５６ で割り切
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　れ、よって、ｎ も１５６で割り切れる。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ｎ は３²×５＝４５でも割り切れるので、ｎ は、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　２３４０の倍数となる。

　ｎ の素因数に、３ を３個、５ を１個含むとき・・・　σ(ｎ)が、(１＋３＋３²＋３³)(１＋５)で割り切
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　れるので、２σ(ｎ)は、２×４０×６＝４８０ で割
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　り切れ、よって、ｎ は９６で割り切れる。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ｎ は３³×５＝１３５でも割り切れるので、ｎ は、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　４３２０の倍数となる。

　ｎ の素因数に、３ を４個以上、５ を１個含むとき・・・　σ(ｎ)は、６で割り切れるので、２σ(ｎ)は、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　１２で割り切れ、よって、ｎ は１２で割り切
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　れる。 ｎ は３⁴×５＝４０５でも割り切れる
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ので、ｎ は、１６２０の倍数となる。

　ｎ の素因数に、 ５ を２個含むとき・・・　σ(ｎ)が、１＋５＋５² ＝３１で割り切れるので、２σ(ｎ)
　　　　　　　　　　　　　　　　　　　　　　　は、２×３１＝６２ で割り切れ、よって、ｎ も６２で割り切
　　　　　　　　　　　　　　　　　　　　　　　れる。ｎ は５²＝２５でも割り切れるので、ｎ は、１５５０の
　　　　　　　　　　　　　　　　　　　　　　　倍数となる。

　ｎ の素因数に、 ５ を３個含むとき・・・　σ(ｎ)が、１＋５＋５²＋５³ ＝１５６で割り切れるので、
　　　　　　　　　　　　　　　　　　　　　　　２σ(ｎ)は、２×１５６＝３１２ で割り切れ、よって、ｎ も
　　　　　　　　　　　　　　　　　　　　　　　３１２で割り切れる。ｎ は５³＝１２５でも割り切れるので、
　　　　　　　　　　　　　　　　　　　　　　　ｎ は、３９０００の倍数となる。

　ｎ の素因数に、 ５ を４個以上含むとき・・・　ｎ は２で割り切れ、かつ、５⁴＝６２５で割り切れ
　　　　　　　　　　　　　　　　　　　　　　　　　　るので、ｎ は、１２５０の倍数となる。

　以上により、
　　　　　　　　　　２４０　、１２５０　、１５５０　、１６２０　、２３４０　、４３２０　、　３９０００
の倍数を調べれば十分であることが分かった。

　調査は以下のように行った。

（１） ４〜３３２億までは偶数を全て調査

　　　　この結果発見されたものが、

　　　　　　　　２４　、９１９６３６４８　、１０２００２３６０３２

　　　の３つである。

（２）３３２億〜１兆までは、

　　　　２４０　、１２５０　、１５５０　、１６２０　、２３４０　、４３２０　、　３９０００

　　の倍数を全て調査

　　　　この結果、２．５倍完全数は存在しなかった。

（３） １兆〜３００兆までは、２¹²×５＝２０４８０ の倍数を全て調査

　　（補足）　２倍完全数〜５倍完全数を素因数分解して調べると、値が大きくなるほど、ほぼ
　　　　　　対数的に比例して２の指数が大きくなる。
　　　　　　　　　　１０２００２３６０３２(約１００億)＝２¹⁴×７×１９×３１×１５１
　　　　　　であることから考えて、１兆以上の数で素因数２の指数が１２未満である２．５倍完
　　　　　　全数が存在する可能性はかなり低いと考えられるので、２¹²の倍数に限定して３００
　　　　　　兆までを検索した。

　　　　この結果、２．５倍完全数は存在しなかった。

　また、ｋ≧３　の時、ｋ倍完全数は有限個と予想されており、最大の３倍完全数〜６倍完全
数は
　　　　３倍完全数　 ５．１×１０¹⁰
　　　　４倍完全数　 １．４×１０³³
　　　　５倍完全数　 ５．５×１０⁷⁶
　　　　６倍完全数　 １．７×１０¹²⁶
とされている。

　この傾向から考えて、２．５倍完全数は、１兆=１０¹²　までに３つ以外は存在せず、３００兆
＝３×１０¹⁴　までにほぼ存在しないことから、２．５倍完全数は見つかった３個で終わりだろ
う、という結論に達したものである。

　ただ、２倍完全数すなわち普通の完全数がとてつもなく大きい値まで見つかっていることを
考えると、必ずしも２．５倍完全数も上記の傾向に従うとは言えないし、「奇数の完全数は存
在しない」「３倍完全数が有限個」というのも証明されていないので、より大きい「図形の完全
数」が存在する可能性は否定出来ない。

　しかし、もし存在するとしても探索で見つけられそうにないので、「３個しか存在しない」を私
の結論にしたいと思う。


（コメント）　らすかるさんの検索結果を読んでいて、大変感動しました。まだ確定ではありま
　　　　　　せんが、「３個しか存在しない」ということを私も信じたい気持ちで一杯です。