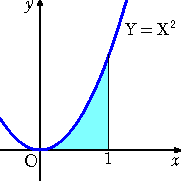
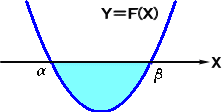
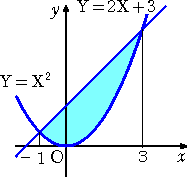丂偙偺儁乕僕偱偼丄尩枾惈傪柍帇偟偰丄弶摍揑側旝暘愊暘傪堦朷偟傛偆偲巚偆丅嬌尷偺掕媊偐
傜巒傑傞偺偑晛捠偩偑丄偙偙偱偼堦愗妱垽偟偨丅旝暘愊暘偵懳偡傞張偟曽偲墳梡偺巇曽偑暘
偐傞偙偲傪栚昗偲偟偨丅懡暘俁帪娫傎偳偱丄旝暘愊暘偺偁傜傑偟偑棟夝偝傟傞傕偺偲巚偆丅
侾丏娭悢偵偮偄偰
丂偙偺儁乕僕偱埖偆娭悢偼丄倎倃
2亄倐倃亄們丂偺傛偆側懡崁幃娭悢偵尷掕偡傞丅娭悢偼丄
俥(X) 亖 倎倃
2亄倐倃亄們丂偺傛偆偵丄婰崋丂
俥(X)丂傪梡偄偰昞偝傟傞丅
俀丏娭悢偺抣偺寁嶼
丂娭悢 俥(X) 偵懳偟偰丄倃亖倎 偺偲偒偺娭悢偺抣傪丄
俥(倎) 偲昞偡丅
乮椺乯丂俥(X) 亖俀 偵懳偟偰偼丄俥(侽) 亖俀丂偲側傞丅
丂丂丂丂俥(X) 亖俀倃亄俁 偵懳偟偰偼丄俥(侽) 亖俀丒侽亄俁亖俁丂偲側傞丅
俁丏摫娭悢偲尨巒娭悢
丂娭悢 俧(X) 亖 倃
値 偵懳偟偰丄娭悢 俥(X) 亖 値倃
値亅侾 傪丄俧(X) 偺
摫娭悢偲偄偄丄俧(X) 偵懳偟
偰丄俥(X) 傪媮傔傞偙偲傪丄乽
旝暘偡傞乿偲偄偆丅摫娭悢 俥(X) 偼 俧乫(X) 偲傕昞偝傟傞丅
丂媡偵丄俧乫(X) 亖 俥(X) 偲側傞娭悢 俧(X) 傪丄娭悢 俥(X) 偺
尨巒娭悢偲偄偄丄俥(X) 偵懳偟偰丄
俧(X) 傪媮傔傞偙偲傪丄乽
愊暘偡傞乿偲偄偆丅尨巒娭悢 俧(X) 偼
晄掕愊暘偲傕偄傢傟丄
丂丂
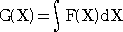
偲昞偝傟傞丅
乮椺乯丂
乮侾乯乫亖侽丂丄丂乮倃乯乫亖侾丂丄丂乮倃2乯乫亖俀倃丂丄丂乮倃3乯乫亖俁倃2
丂
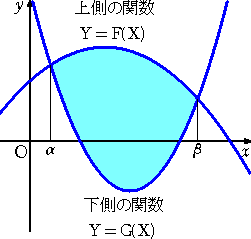
 係丏摫娭悢偲尨巒娭悢偺慄宍惈
係丏摫娭悢偲尨巒娭悢偺慄宍惈
丂
榓乮嵎乯偺旝暘偼丄旝暘偺榓乮嵎乯偵摍偟偔丄幚悢攞偺旝暘偼丄旝暘偺幚悢攞偵摍偟偄丅
丂榓乮嵎乯偺愊暘偼丄愊暘偺榓乮嵎乯偵摍偟偔丄幚悢攞偺愊暘偼丄愊暘偺幚悢攞偵摍偟偄丅
偙偺惈幙偐傜丄師偺傛偆側旝暘愊暘偺寁嶼偑壜擻偲側傞丅
乮椺乯丂
乮俀倃亄俁乯乫亖乮俀倃乯乫亄乮俁乯乫亖俀乮倃乯乫亄俁乮侾乯乫亖俀丒侾亄俁丒侽亖俀
丂
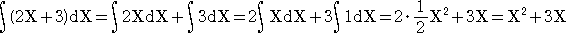 俆丏旝暘學悢偺寁嶼
俆丏旝暘學悢偺寁嶼
丂娭悢 俥(X) 偵懳偟偰丄偦偺摫娭悢 俥乫(X) 偺 倃亖倎 偺偲偒偺抣
俥乫(倎) 傪丄旝暘學悢偲偄偆丅
乮椺乯丂娭悢 俥(X)亖倃
3亅俀倃 偵懳偟偰丄旝暘學悢 俥乫乮亅侾乯偼丄師偺庤弴偱媮傔傜傟傞丅
丂娭悢 俥(X) 傪旝暘偟偰丄摫娭悢 俥乫(X) 偼丄俥乫(X)亖俁倃
2亅俀
丂偙偺 倃 偵 亅侾 傪戙擖偟偰丄俥乫(亅侾)亖俁乮亅侾乯
2亅俀 亖俁亅俀 亖侾
俇丏旝暘學悢偺婔壗妛揑堄枴
丂娭悢 俥(X) 偵懳偟偰丄旝暘學悢 俥乫乮倎乯 偼丄
嬋慄丂倄亖 俥(X) 偺丄倃亖倎 偵偍偗傞愙慄偺孹偒
傪昞偡丅
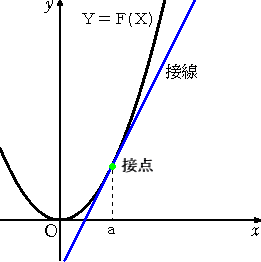
乮椺乯丂曻暔慄 倄亖倃2 偺僌儔僼偲丄俁杮偺捈慄
丂丂丂乮侾乯丂倄亖俀倃
丂丂丂乮俀乯丂倄亖俀倃亅侾
丂丂丂乮俁乯丂倄亖俀倃亅俀 |
|
 |
偺偦傟偧傟偲偺埵抲娭學偐傜丄愙偡傞忬懺偲偄偆傕偺傪棟夝偟傛偆丅 |
丂丂
 |
丂丂倄亖倃2 偺僌儔僼偲捈慄 倄亖俀倃 偼丄
丂丂倃2亖俀倃 偐傜丄倃亖侽丄俀丂側偺偱丄
丂丂堎側傞俀揰偱岎傢傞丅
丂丂倄亖倃2 偺僌儔僼偲捈慄 倄亖俀倃亅侾 偼丄
丂丂倃2亖俀倃亅侾 偐傜丄倃亖侾丂側偺偱丄
丂丂侾揰偱愙偡傞丅
丂丂倄亖倃2 偺僌儔僼偲捈慄 倄亖俀倃亅俀 偼丄
丂丂倃2亖俀倃亅俀 傪枮偨偡幚悢偼側偄偺偱丄
丂丂岎傢傜側偄丅
丂埲忋偐傜丄
曻暔慄 倄亖倃2 偺僌儔僼偲捈慄 倄亖俀倃亅侾丂偼丄
揰乮侾丆侾乯偱愙偟丄 倄亖俀倃亅侾丂偑愙慄偲側傞丅
丂偲偙傠偱丄俥乮倃乯亖倃2 偲偍偔偲丄俥乫乮侾乯亖俀丂偱
偁傞丅偙傟偼丄愙慄 倄亖俀倃亅侾 偺孹偒偵摍偟偄丅 |
丂愙慄偼丄愙揰晅嬤偵偍偗傞嬋慄偺忬懺傪丄捈慄偲偟偰嬤帡偡傞偲偄偆堄枴偵偍偄偰丄戝愗側
峫偊曽偱偁傞丅旝暘傪妛廗偡傞慜偺抜奒偱偼丄曻暔慄偺愙慄偼丄敾暿幃傪妶梡偟偰媮傔傞偺
偑晛捠偱偁傞偑丄堦搙旝暘傪妛廗偡傞偲丄愙慄偼丄旝暘學悢偺婔壗妛揑堄枴傪棙梡偟偰丄娙
扨偵媮傔傜傟傞傛偆偵側傞丅
乮椺乯丂曻暔慄 倄亖倃
2亅俀倃亅侾 忋偺揰乮俁丆俀乯偵偍偗傞愙慄偺曽掱幃傪媮傔傛丅
丂倄乫亖俀倃亅俀丂側偺偱丄倃亖俁丂偺偲偒丄倄乫亖俀丒俁亅俀亖係
傛偭偰丄孹偒 係 偱丄揰乮俁丆俀乯傪捠傞捈慄偺曽掱幃偼丄倄亖係乮倃亅俁乯亄俀亖係倃亅侾侽
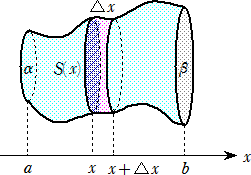
俈丏娭悢偺憹尭
丂愙慄偼丄愙揰晅嬤偵偍偗傞嬋慄偺忬懺傪丄捈慄偲偟偰嬤帡偟偰偄傞偺偱丄愙慄偺孹偒傪昞偡
旝暘學悢 俥乫乮倎乯 偺惓晧偺晞崋偐傜丄 倃亖倎 偵偍偗傞娭悢 俥(X) 偺憹尭偺忬懺傪抦傞偙偲偑
偱偒傞丅偡側傢偪丄
丂俥乫乮倎乯亜侽丂側傜偽丄倃亖倎 偺嬤偔偱丄娭悢 俥(X) 偼憹壛偺忬懺
丂俥乫乮倎乯亙侽丂側傜偽丄倃亖倎 偺嬤偔偱丄娭悢 俥(X) 偼尭彮偺忬懺
乮椺乯丂俥乮倃乯亖倃
2丂偵偍偄偰丄俥乫乮倃乯亖俀倃
丂倃亜侽丂偱偼丄偄偮傕丂俥乫乮倃乯亖俀倃亜侽丂側偺偱丄倃亜侽丂偵偍偄偰丄俥乮倃乯偼憹壛娭悢
丂倃亙侽丂偱偼丄偄偮傕丂俥乫乮倃乯亖俀倃亙侽丂側偺偱丄倃亙侽丂偵偍偄偰丄俥乮倃乯偼尭彮娭悢
丂摫娭悢偺晞崋傪挷傋傞偙偲偵傛傝丄娭悢偺憹尭偺忬懺偑暘偐傞偲偄偆偙偲偼丄夋婜揑側偙偲
偱偁傞丅偙偺応崌丄憹尭偺曄傢傝栚偺寁嶼偑億僀儞僩偵側傞丅
丂忋偺乮椺乯偐傜傕暘偐傞傛偆偵丄倃亖侽丂偱丄尭彮偐傜憹壛偵忬懺偑曄壔偟偰偄傞丅偙偺憹尭
偺曄傢傝栚 倃亖侽丂偼丄摫娭悢 俥乫乮倃乯亖俀倃
亖侽丂偲偡傞偙偲偵傛傝丄媮傔傜傟傞丅乮幚嵺偵丄
憹尭偑曄壔偟偰偄傞偐偳偆偐偼丄廃傝偺抣偺曄壔傪挷傋傞昁梫偑偁傞丅乯
乮椺乯丂娭悢 俥乮倃乯亖倃
3亅俁倃 偺憹尭傪挷傋傛丅
丂俥乫乮倃乯亖俁倃
2亅俁亖俁乮倃亄侾)(倃亅侾乯亖侽丂傛傝丄倃亖亅侾丄侾
俥乫乮倃乯亜侽丂傪夝偄偰丄倃亙亅侾丄侾亙倃丂丂丂丂丂俥乫乮倃乯亙侽丂傪夝偄偰丄亅侾亙倃亙侾
傛偭偰丄倃亙亅侾丄侾亙倃丂偺偲偒丄俥乫乮倃乯亜侽丂偐傜丄俥乮倃乯偼憹壛娭悢
丂亅侾亙倃亙侾丂偺偲偒丄俥乫乮倃乯亙侽丂偐傜丄俥乮倃乯偼尭彮娭悢
丂埲忋偺娭悢偺憹尭偺忬懺偼丄師偺傛偆側
憹尭昞偵傑偲傔傜傟傞丅
丂丂

丂憹尭昞偵偍偄偰丄倃亖亅侾 偺慜屻偱丄憹壛偐傜尭彮偵曄壔偟偰偄傞丅偙偺傛偆側偲偒丄
倃亖亅侾 偱丄娭悢 俥乮倃乯偼
嬌戝偱偁傞偲偄偄丄
嬌戝抣偼丄俀丂偲側傞丅
摨條偵丄倃亖侾 偺慜屻偱丄尭彮偐傜憹壛偵曄壔偟偰偄傞丅偙偺傛偆側偲偒丄
倃亖侾 偱丄娭悢 俥乮倃乯偼
嬌彫偱偁傞偲偄偄丄
嬌彫抣偼丄亅俀丂偲側傞丅
丂嬌戝抣丒嬌彫抣偼丄嬊強揑側堄枴偱偺嵟戝抣丒嵟彫抣偺偙偲偱偁傞丅嬌戝抣丒嬌彫抣偼丄
傑偲傔偰丄
嬌抣偲偄傢傟傞丅
乮捛婰乯丂椷榓俇擭侾侾寧俀俇擔晅偗
丂師偺搶杒戝妛丂暥宯乮侾俋俉俇乯偺栤戣偼丄嬌彫抣偺寁嶼偱偁傞丅
栤戣丂丂倎 偼幚悢偲偟丄俥乮倶乯亖倎乮倶亅侾乯
2乮倶亄侾乯亄倶 偲偡傞丅倎 偺娭悢
丂丂 俧乮倎乯亖佺
-11 乷俥乫乮倶乯乸
3倓倶 偺嬌彫抣傪媮傔傛丅
乮夝乯丂俥乮倶乯亖倎倶
3亅倎倶
2亄乮侾亅倎乯倶亄倎丂傛傝丄俥乫乮倶乯亖俁倎倶
2亅俀倎倶亄乮侾亅倎乯
乷俥乫乮倶乯乸
3亖乮俁倎倶
2亅俀倎倶乯
3亄俁乮侾亅倎乯乮俁倎倶
2亅俀倎倶乯
2亄俁乮侾亅倎乯
2乮俁倎倶
2亅俀倎倶乯亄乮侾亅倎乯
3
佺
-11 乷俥乫乮倶乯乸
3倓倶 偺寁嶼偱丄佺
-11 乮倶 偺婏悢師偺崁乯倓倶 亖侽丂側偺偱丄乷俥乫乮倶乯乸
3 偺嬼
悢師偺崁偩偗偵拲栚偡傟偽傛偄丅
丂俀俈倎
3倶
6亄俁俇倎
3倶
4亄俀俈倎
2乮侾亅倎乯倶
4亄侾俀倎
2乮侾亅倎乯倶
2亄俋倎乮侾亅倎乯
2倶
2亄乮侾亅倎乯
3
傛傝丄
俧乮倎乯亖俀佺
01 乷俀俈倎
3倶
6亄俁俇倎
3倶
4亄俀俈倎
2乮侾亅倎乯倶
4亄侾俀倎
2乮侾亅倎乯倶
2亄俋倎乮侾亅倎乯
2倶
2亄乮侾亅倎乯
3乸倓倶
亖俀乮俀俈倎
3/俈亄俁俇倎
3/俆亄俀俈倎
2乮侾亅倎乯/俆亄係倎
2乮侾亅倎乯亄俁倎乮侾亅倎乯
2亄乮侾亅倎乯
3乯
亖乮俀俆俇/俁俆乯倎
3亄乮俇係/俆乯倎
2亄俀
俧乫乮倎乯亖乮俈俇俉/俁俆乯倎
2亄乮侾俀俉/俆乯倎亖乮俈俇俉/俁俆乯倎乮倎亄俈/俇乯亖侽丂傛傝丄倎亖亅俈/俇丄侽
俧乮倎乯偼丄倎亖侽丂偱嬌彫偱丄嬌彫抣偼丄俧乮侽乯亖俀丂偱偁傞丅丂丂乮廔乯
乮僐儊儞僩乯丂寁嶼偺曽恓偼丄扨弮柧夣偱偁傞偑丄寁嶼偦偺傕偺偑彮偟戝曄偱偁傞丅
俉丏娭悢偺僌儔僼
丂憹尭昞傪棙梡偟偰丄娭悢偺僌儔僼傪昤偔偙偲偑偱偒傞丅
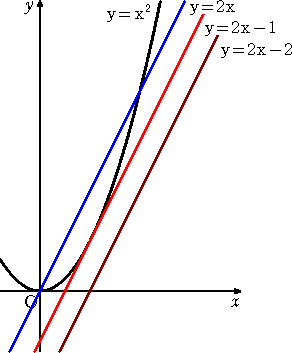
乮椺乯丂娭悢 俥乮倃乯亖倃3亅俁倃2亄俀丂偺僌儔僼傪偐偗丅
丂俥乫(倃乯亖俁倃2亅俇倃 亖俁倃乮倃亅俀乯亖侽丂傛傝丄
丂丂丂丂丂丂丂倃亖侽丄俀
傛偭偰丄師偺憹尭昞傪摼傞丅
丂丂
偟偨偑偭偰丄媮傔傞僌儔僼偼塃忋恾偲側傞丅 |
|
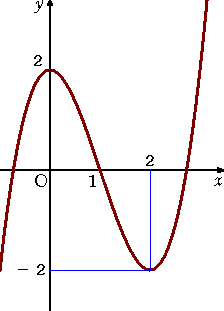 |
乮捛婰乯丂椷榓俈擭俆寧俀係擔晅偗
丂師偺搶杒戝妛丂屻婜暥宯乮侾俋俋俁乯偺栤戣偼丄嬌戝抣丒嬌彫抣偺寁嶼偱偁傞丅
栤戣丂丂娭悢 俥乮倶乯亖佺
xx+1 俁倲
2乮倲亄侾乯乮倲亅侾乯倓倲 偺嬌戝抣丄嬌彫抣傪偟傜傋丄倷亖俥乮倶乯偺
丂丂僌儔僼偺奣宍傪偐偗丅
乮夝乯丂俥乮倶乯亖佺
xx+1 乮俁倲
4亅俁倲
2乯倓倲亖[乮俁/俆乯倲
5亅倲
3]
xx+1
丂亖乮俁/俆乯乮乮倶亄侾乯
5亅倶
5乯亅乮倶亄侾乯
3亄倶
3丂傛傝丄
丂俥乫乮倶乯亖俁乮乮倶亄侾乯
4亅倶
4亅乮倶亄侾乯
2亄倶
2乯亖俇倶乮倶亄侾乯乮俀倶亄侾乯亖侽丂偲偍偔偲丄
丂倶亖亅侾丄亅侾/俀丄侽
傛偭偰丄憹尭昞偼丄
丂丂

倶亖亅侾偺偲偒嬌彫偱丄嬌彫抣丂俥乮亅侾乯亖俁/俆亅侾亖亅俀/俆
倶亖侽偺偲偒嬌彫偱丄嬌彫抣丂俥乮侽乯亖俁/俆亅侾亖亅俀/俆
倶亖亅侾/俀偺偲偒嬌戝偱丄嬌戝抣
丂俥乮亅侾/俀乯亖乮俁/俆乯乮侾/俁俀亄侾/俁俀乯亅侾/俉亅侾/俉亖亅侾俈/俉侽
埲忋偐傜丄倷亖俥乮倶乯偺僌儔僼偺奣宍偼丄
丂丂
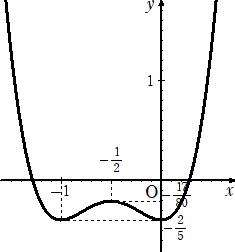
丂丂乮廔乯
俋丏柺愊偲掕愊暘
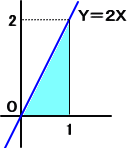 |
丂丂丂嵍恾偺嶰妏宍偺柺愊偼丄乮掙曈乯亊乮崅偝乯亐俀亖侾亊俀亐俀亖侾
丂丂偱偁傞丅
丂丂丂偲偙傠偱丄倄亖俀倃 偺尨巒娭悢 俧乮倃乯 偼丄俧乮倃乯亖倃2
丂丂偙偺偲偒丄俧乮侽乯亖侽丄俧乮侾乯亖侾丂側偺偱丄俧乮侾乯亅俧乮侽乯亖侾
丂丂丂偙偺俀偮偺寁嶼寢壥偑摍偟偄偙偲偵拲堄偡傞丅
丂丂丂忋婰偺寁嶼偑帵嵈偡傞傛偆偵丄愊暘偵傛傞柺愊偺寁嶼偑壜擻偲
丂丂側傞丅乮傕偆彮偟堦斒揑側応崌偼丄偙偪傜傪嶲徠乯 |
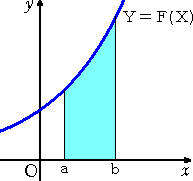 |
丂丂偮傑傝丄嵍恾偺傛偆側恾宍偺柺愊偼丄
丂丂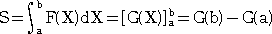
丂偵傛傝媮傔傜傟傞丅偨偩偟丄俧(倃) 偼丄俥(倃) 偺尨巒娭悢偲
丂偡傞丅
丂丂偙偙偱丄俽偺幃偵偍偗傞愊暘寁嶼傪丄掕愊暘偺寁嶼偲
丂偄偆丅
|
乮椺乯丂塃恾偺傛偆側恾宍偺柺愊傪媮傔傛丅
丂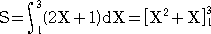
丂丂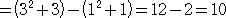
乮拲乯丂塃恾偺恾宍偼戜宍側偺偱丄柺愊偼丄丂丂
丂丂丂俽亖乮俁亄俈乯亊俀亐俀亖侾侽丂偱偁傞丅
乮椺乯丂壓恾偺傛偆側恾宍偺柺愊傪媮傔傛丅
|
|
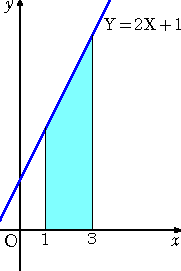 |
乮暿夝乯丂嬫暘媮愊朄揑側曽朄偱峫偊傞丅
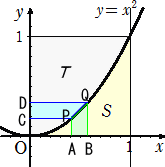 |
丂丂嵍恾偵偍偄偰丄曻暔慄 倷亖倶2 忋偺揰俹乮倶丆倶2乯偲偪傚偭偲偢傜
丂丂偟偨曻暔慄忋偺揰俻乮倶亄儮丆乮倶亄儮乯2乯傪偲傞丅
丂丂戜宍ABQP偺柺愊俲偼丄
丂丂儮乮倶2亄乮倶亄儮乯2乯/俀亖儮乮俀倶2亄俀儮倶亄儮2乯/俀
丂丂戜宍CPQD偺柺愊俫偼丄
丂丂乮乮倶亄儮乯2亅倶2乯乮倶亄乮倶亄儮乯乯/俀亖儮乮俀倶亄儮乯2/俀 |
丂偦偙偱丄丂俫/俲亖乮俀倶亄儮乯
2/乮俀倶
2亄俀儮倶亄儮
2乯丂偵偍偄偰丄儮佮侽偲偡傞偲丄俫/俲佮俀
丂偙偺偙偲偐傜丄丂俿 丗 俽 亖 俀 丗 侾丂偡側傢偪丄丂俽亖侾/俁丂偑惉傝棫偮偙偲偑暘偐傞丅丂乮廔乯
乮僐儊儞僩乯丂偙偺暿夝偺峫偊曽傕崻掙偵偼
僇償傽儕僄儕偺尨棟偑懚嵼偡傞丅
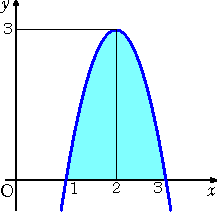
侾侽丏掕愊暘偺寁嶼
丂娭悢 俥乮倃乯偵偍偄偰丄俥乮倃乯亞侽 偺偲偒丄掕愊暘偺寁嶼偼丄柺愊偺寁嶼偲偄偆堄枴傪帩偭偨
偑丄掕愊暘偺寁嶼偼丄堦斒偺娭悢偵懳偟偰傕丄峴偆偙偲偑偱偒傞丅偨偩偟丄偦偺寁嶼寢壥偼丄
柺愊偲偄偆堄枴傪帩偨側偄偙偲偵拲堄偡傞丅
乮椺乯
丂丂丂丂
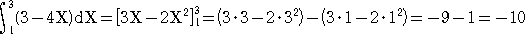 侾侾丏柺愊偺寁嶼
侾侾丏柺愊偺寁嶼
丂偙偙偱偼丄偄偔偮偐偺柺愊偺岞幃傪徯夘偡傞丅
乮侾乯
 |
丂丂丂嵍恾偺傛偆側丄曻暔慄偲倃幉偑埻傓恾宍偺柺愊偼丄
丂丂丂丂 |
丂丂偙偺柺愊偼丄忋恾偺挿曽宍偺柺愊偺俀/俁攞偱傕偁傞丅
丂偙偺榖戣偑丄
搶杒戝妛暥宯乮侾俋俈俆乯偱弌戣偝傟偨丅
丂偙偺柺愊偺岞幃傪梡偄傞偲丄壓恾偺傛偆側恾宍偺柺愊偼丄埫嶼偱媮傔傜傟傞丅
 |
丂丂丂媮傔傞柺愊偼丄
丂丂丂丂丂俽亖乮俁亅侾乯亊俁亊(俀/俁) 亖係
|
乮俀乯
 |
丂丂嵍恾偺傛偆側応崌丄媮傔傞柺愊偼丄
丂丂丂丂丂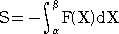 |
丂傑偨丄偙偺寁嶼偼丄師偺傛偆偵夝庍偝傟傞丅
丂丂丂

 |
丂丂丂丂堦斒偵丄嵍恾偺傛偆側恾宍偵懳偟偰丄
丂丂丂媮傔傞柺愊偼丄
丂丂丂丂丂丂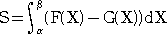
丂丂丂偱梌偊傜傟傞丅 |
乮椺乯
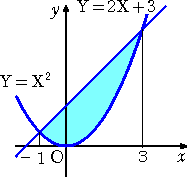 |
丂曻暔慄 倄亖倃2 偲捈慄 倄亖俀倃亄俁 偑埻傓恾宍偺柺愊傪
丂丂丂媮傔傛丅
丂倃2 亖俀倃亄俁丂傛傝丄乮倃亅俁)(倃亄侾乯亖侽丂傛偭偰丄倃亖俁丄亅侾
丂偟偨偑偭偰丄媮傔傞柺愊偼丄 |
丂丂丂
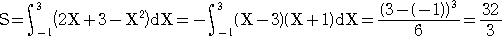 侾俀丏懖嬈帋尡栤戣
侾俀丏懖嬈帋尡栤戣
丂丂嬋慄 倄亖倃
3 偵偮偄偰丄師偺栤偵摎偊傛丅
乮侾乯丂嬋慄忋偺揰乮侾丆侾乯偵偍偗傞愙慄偺曽掱幃傪媮傔傛丅
乮俀乯丂嬋慄偲乮侾乯偺愙慄偲偺岎揰偺倃嵗昗傪媮傔傛丅
乮俁乯丂嬋慄偲愙慄偱埻傑傟偨恾宍偺柺愊傪媮傔傛丅
乮摎乯丂乮侾乯丂倄亖俁倃亅俀丂乮俀乯丂倃亖亅俀丄侾丂乮俁乯丂27/係
丂傒側偝傫丄柍帠偵懖嬈偱偒偨偱偟傚偆偐丠
乮偍婅偄乯丂偙偺儁乕僕偺僞僀僩儖捠傝丄旝暘愊暘偑俁帪娫偱儅僗僞乕偱偒偨偐偳偆偐偵偮偄偰丄
丂丂傾儞働乕僩傪庢傝偨偄偲巚偄傑偡丅強梫帪娫傪丄
偙偪傜傑偱儊乕儖偱偍婅偄偟傑偡丅傾儞働
丂丂乕僩偺寢壥偵傛偭偰偼丄傕偟偐偟偨傜僞僀僩儖偑曄峏偵側傞偐傕偟傟傑偣傫丏丏丏丏丏
f(^_^)丂丅
乮捛婰乯丂俫俶乽僐儖儉乿偝傫偐傜丄旝暘愊暘偵偮偄偰丄乽懱愊乿偑側偄傛丄偲偺偛巜揈傪捀偄偨丅
丂丂丂丂埲壓丄僐儖儉偝傫偵傛傞傕偺偱偡丅乮堦晹暥尵摍傪廋惓偝偣偰偄偨偩偒傑偟偨丅乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮暯惉俀俈擭侾俀寧侾擔晅偗乯
丂埲壓偺婰弎偼丄捈姶揑側棟夝傪彆偗傞傕偺偱偁偭偰尩枾側愢柧偱偼側偄偙偲傪梊傔偍抐傝
偟偰偍偒傑偡丅
侾俁丏懱愊
丂倶幉偵悅捈側俀暯柺兛丄兝偵嫴傑傟偨棫懱偺懱愊傪V偲偡傞丅俀暯柺兛丄兝偲倶幉偲偺岎揰
偺嵗昗傪偦傟偧傟倎丄倐偲偡傞丅偨偩偟丄倎亙倐偲偡傞丅嵗昗偑倶偱偁傞揰傪捠傝丄倶幉偵悅捈側
暯柺偱偺棫懱偺愗傝岥偺柺愊傪俽乮倶乯偲偡傞丅倶偺憹暘嚈倶偵懳偡傞V偺憹暘傪嚈V偲偡傞丅
丂
丂嚈倶偑廫暘彫偝偄偲偒偼丄嚈V佮S(x)嚈倶丂側偺偱丄嬫暘媮愊朄偺峫偊偵傛傝
丂丂倁亖lim
嚈倶仺侽 儼S(x)嚈倶亖佺
ab S乮x)倓倶
偲峫偊傜傟傞丅
椺丂掙柺偺敿宎 倰 丄崅偝 倛 偺捈墌悕偺懱愊傪媮傔傛丅
丂捈墌悕偺捀揰傪尨揰偲偟丄捀揰偐傜捈墌悕偺掙柺偺拞怱偵岦偐偆捈慄傪 倶 幉偲偡傞丅
丂暯柺 倶亖倲 偱愗抐偟偨愗傝岥偺恾宍偼墌偱丄偦偺柺愊偼丄丂S(倲)亖兾乮倰/倛乯
2倲
2
丂傛偭偰丄媮傔傞棫懱偺懱愊偼丄
丂丂佺
0h S乮x)倓倶亖佺
0h 兾乮倰/倛乯
2倲
2倓倶亖兾乮倰/倛乯
2丒乮倛
3/俁乯亖兾倰
2倛/俁
偲側傝丄傛偔抦傜傟偨岞幃傪摼傞丅
乮捛婰乯丂椷榓俈擭侾寧侾俀擔晅偗
侾係丏懍偝丒摴偺傝偺栤戣
丂師偺搶杒戝妛丂棟宯乮侾俋俉俋乯偺栤戣偼丄暔棟傊偺墳梡栤戣偱偁傞丅
栤戣俁丂丂嬋慄 倶亖俥乮倷乯 乮侽亝倷亝俁侽乯 傪倷幉偺傑傢傝偵夞揮偟偰偱偒傞掙偺暯傜側嬻偺梕
丂丂婍偑偁傞丅埲壓丄挿偝偺扨埵傪侾們倣偲偡傞丅偙偺梕婍偵枅昩 倎 們倣
3偺妱崌偱悈傪擖傟
丂丂傞偲偒丄偁傆傟弌偡傑偱偼 倲 昩屻偺悈柺偺忋徃懍搙偑 侾/併乮侾亄倲乯 們倣/昩偱偁傞偲偡
丂丂傞丅
乮侾乯丂壗昩屻偵悈柺偺崅偝偑侾俉們倣偵側傞偐丅
乮俀乯丂娭悢俥乮倷乯傪媮傔傛丅偨偩偟丄俥乮倷乯偼惓偺抣傪偲傞傕偺偲偡傞丅
乮夝乯乮侾乯丂倲 昩屻偺悈柺偺崅偝傪 倷乮們倣乯偲偍偔偲丄丂戣堄傛傝丄丂倓倷/倓倲亖侾/併乮侾亄倲乯
偙偺偲偒丄丂倷亖俀併乮侾亄倲乯亄俠丂乮俠偼愊暘掕悢乯
倲亖侽丂偺偲偒丄倷亖侽丂側偺偱丄丂俠亖亅俀丂傛傝丄丂倷亖俀併乮侾亄倲乯亅俀
倷亖侾俉丂偺偲偒丄丂俀併乮侾亄倲乯亅俀亖侾俉丂傛傝丄丂侾亄倲亖侾侽侽丂偡側傢偪丄丂倲亖俋俋乮昩屻乯
乮俀乯丂倲 昩屻偺梕婍偺懱愊傪倁偲偍偔偲丄丂倁亖兾佺
0y 倶
2倓倷亖兾佺
0y 俥
2乮倷乯倓倷
傛偭偰丄丂倓倁/倓倲亖乮倓倁/倓倷乯丒乮倓倷/倓倲乯亖兾俥
2乮倷乯丒侾/併乮侾亄倲乯亖倎丂傛傝丄
丂俥
2乮倷乯亖乷倎併乮侾亄倲乯乸/兾亖倎乮倷亄俀乯/乮俀兾乯
偟偨偑偭偰丄丂俥乮倷乯亖併乷倎乮倷亄俀乯/乮俀兾乯乸丂丂乮廔乯
丂丂
埲壓丄岺帠拞両







 丂丂乮廔乯
丂丂乮廔乯