△ＡＢＣの内部の点Ｘに対して、次の事実が知られている。
定 理 △ＡＢＣの内部の点Ｘに対して、∠ＸＡＢ、∠ＸＢＣ、∠ＸＣＡのうち、３０°以下
のものが存在する。
定理を見て至極当然のような気もする。そのような点Ｘは必ず存在するような．．．雰囲気！
どんな三角形でも言えるよ、という点が大切なのだろう。
この定理を示すために、ブロカール点という概念が活躍する。
（第一）ブロカール（Brocard）点とは、△ＡＢＣに対して、∠ＰＡＢ＝∠ＰＢＣ＝∠ＰＣＡ を
満たす点をいう。この点は確かに存在することが次の図を見れば了解されるだろう。
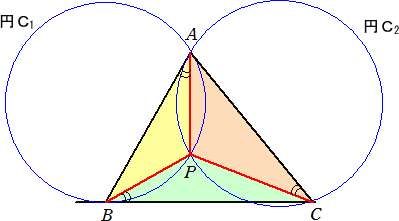
円Ｃ1 は、点Ｂで辺ＢＣに
接し、円Ｃ2は、点Ａで辺ＡＢ
に接する。
接弦定理により、
∠ＰＡＢ＝∠ＰＢＣ＝∠ＰＣＡ
が成り立つ。
同様に、△ＡＢＣに対して、∠ＰＢＡ＝∠ＰＣＢ＝∠ＰＡＣ を満たす点を（第二）ブロカール
点という。
ブロカール点という言葉を初めて知ったのは、平成２５年１１月２３日（祝）に、筑波大学付
属駒場高校で行われた研究集会においてであった。
数学の控室として利用された５０周年記念会館に、「ブロカール点の応用」と題した、筑波
大学付属駒場高校 富士晃成さんのパネルが掲示されていた。このパネルは、「身の回り
の現象を数理の目で見る！」というテーマのもとに開催されている、高校生による研究発表
会：「第3回 高校生によるMIMS現象数理学研究発表会」（平成25年10月13日 明治大学中
野キャンパス）に展示されたものらしい。
パネルに書かれている推論が少し不明確に感じたので、厳密に示したいという思いが、こ
のページを起こしたきっかけである。
上記の定理を示すには、点Ｘをブロカール点と考えて示せば十分である。即ち、
△ＡＢＣにおいて、ＢＣ＝ａ、ＣＡ＝ｂ、ＡＢ＝ｃ とおく。△ＡＢＣのブロカール点Ｘに対して、
ＸＡ＝ｐ、ＸＢ＝ｑ、ＸＣ＝ｒ とおく。∠ＸＡＢ＝∠ＸＢＣ＝∠ＸＣＡ＝θとし、△ＡＢＣの面積をＳと
おく。
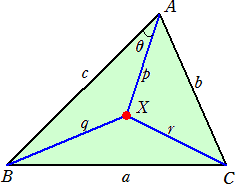
このとき、次の補題が成り立つ。
補 題 ｃｏｔθ＝（ａ2＋ｂ2＋ｃ2）/(４Ｓ)＝ｃｏｔＡ＋ｃｏｔＢ＋ｃｏｔＣ
（証明） △ＸＡＢ＝ｐｑｃ/（４Ｒ’） （Ｒ’は△ＸＡＢの外接円の半径） より、
４△ＸＡＢ＝ｐｑｃ/Ｒ’＝２ｐｃｓｉｎθ＝２ｐｃｃｏｓθ/ｃｏｔθ＝（ｐ2＋ｃ2−ｑ2）/ｃｏｔθ
同様にして、 ４△ＸＢＣ＝（ｑ2＋ａ2−ｒ2）/ｃｏｔθ 、４△ＸＣＡ＝（ｒ2＋ｂ2−ｐ2）/ｃｏｔθ
辺々加えて、４Ｓ＝（ａ2＋ｂ2＋ｃ2）/ｃｏｔθ 即ち、ｃｏｔθ＝（ａ2＋ｂ2＋ｃ2）/(４Ｓ) が成り立つ。
また、ＡからＢＣに下ろした垂線の足をＤとすると、
ｃｏｔＢ＋ｃｏｔＣ＝ＢＤ/ＡＤ＋ＤＣ/ＡＤ＝ＢＣ/ＡＤ
ここで、Ｓ＝ＢＣ・ＡＤ/２ より、ＡＤ＝２Ｓ/ＢＣ なので、
ｃｏｔＢ＋ｃｏｔＣ＝ＢＣ2/（２Ｓ）＝ａ2/（２Ｓ）
同様にして、 ｃｏｔＣ＋ｃｏｔＡ＝ｂ2/（２Ｓ） 、ｃｏｔＡ＋ｃｏｔＢ＝ｃ2/（２Ｓ）
辺々加えて、 ２（ｃｏｔＡ＋ｃｏｔＢ＋ｃｏｔＣ）＝（ａ2＋ｂ2＋ｃ2）/（２Ｓ）
よって、 ｃｏｔＡ＋ｃｏｔＢ＋ｃｏｔＣ＝（ａ2＋ｂ2＋ｃ2）/（４Ｓ） が成り立つ。
以上から、 ｃｏｔθ＝（ａ2＋ｂ2＋ｃ2）/(４Ｓ)＝ｃｏｔＡ＋ｃｏｔＢ＋ｃｏｔＣ が成り立つ。 （証終）
いよいよ定理を証明する準備ができた。
（証明） ここで、Ｃ≦Ｂ≦Ａ としても一般性は失われない。さらに、ＡからＢＣへ下ろした垂
線の足をＤとし、ＡＤ＝１、ＢＤ＝ｘ とおく。このとき、ｃｏｔＢ＝ｘ 、ｃｏｔＣ＝ａ−ｘ より、
ｃｏｔＢ＋ｃｏｔＣ＝ａ である。このとき、
ｃｏｔＡ＋ｃｏｔＢ＋ｃｏｔＣ＝ｃｏｔ（１８０°−（Ｂ＋Ｃ））＋ｃｏｔＢ＋ｃｏｔＣ
＝ｃｏｔＢ＋ｃｏｔＣ−ｃｏｔ（Ｂ＋Ｃ）
＝ｃｏｔＢ＋ｃｏｔＣ−（ｃｏｔＢｃｏｔＣ−１）/（ｃｏｔＢ＋ｃｏｔＣ）
＝ａ−｛ｘ（ａ−ｘ）−１｝/ａ
＝（ｘ2−ａｘ＋ａ2＋１）/ａ
＝｛（ｘ−ａ/２）2＋（
ａ/２−１）2＋ａ｝/ａ≧よって、ｃｏｔθ＝ｃｏｔＡ＋ｃｏｔＢ＋ｃｏｔＣ≧
より、 ｔａｎθ≦１/したがって、θ≦３０°が成り立つ。等号成立は、△ＡＢＣが正三角形のとき。 （証終）
上記証明の別証明を、当ＨＰがいつもお世話になっているＨＮ「Ｋ．Ｓ．」さんより、メールで
頂いた。（平成２６年１月２日付け）
△ＡＢＣの辺をａ、ｂ、ｃ、角をＡ、Ｂ、Ｃとする。
（ａ2＋ｂ2＋ｃ2）/(４Ｓ)＝ｃｏｔＡ＋ｃｏｔＢ＋ｃｏｔＣ≧
の別証明（証明） 余弦定理より、
ａ2＝ｂ2＋ｃ2−２ｂｃ・ｃｏｓＡ 、ｂ2＝ｃ2＋ａ2−２ｃａ・ｃｏｓＢ 、ｃ2＝ａ2＋ｂ2−２ａｂ・ｃｏｓＣ
辺々足して、
ａ2＋ｂ2＋ｃ2＝２ｂｃ・ｃｏｓＡ＋２ｃａ・ｃｏｓＢ＋２ａｂ・ｃｏｓＣ
＝４｛（1/2）ｂｃｓｉｎＡ・ｃｏｔＡ＋（1/2）ｃａｓｉｎＢ・ｃｏｔＢ＋（1/2）ａｂｓｉｎＣ・ｃｏｔＣ｝
＝４Ｓ（ｃｏｔＡ＋ｃｏｔＢ＋ｃｏｔＣ）
（ａ2＋ｂ2＋ｃ2）/（４Ｓ）≧
⇔ （ａ2＋ｂ2＋ｃ2）2/（４Ｓ）2≧３ ⇔ （ａ2＋ｂ2＋ｃ2）2≧３・１６Ｓ2⇔ （ａ2＋ｂ2＋ｃ2）2≧３・（ａ＋ｂ＋ｃ）（−ａ＋ｂ＋ｃ）（ａ−ｂ＋ｃ）（ａ＋ｂ−ｃ）
⇔ ４（ａ4＋ｂ4＋ｃ4−ａ2ｂ2−ｂ2ｃ2−ｃ2ａ2）≧０
⇔ ２｛（ａ2−ｂ2)2＋（ｂ2−ｃ2)2＋（ｃ2−ａ2)2）≧０ （証終）
（追記） 平成２６年１月１８日付け
Ｋ．Ｓ．さんが与えられた証明は、筑波大学付属駒場高校５０周年記念会館に掲示されて
いた、富士晃成さんのパネルで示されていた証明とほとんど同じである。うろ覚えであるが、
次のように論証が進められていたように思う。
（パネルを撮影したが保存するのを忘れてしまい画像が消失してしまった！残念．．(T_T) ）
（別証） この定理を示すには、ブロカール点Ｐに対して、∠ＰＡＢ≦３０°を示せばよい。
三角形の内角の和は、１８０°なので、 ０°≦∠ＰＡＢ≦６０°は明らかだろう。
ここで、△ＡＢＣの面積をＳ、３辺の長さを ＢＣ＝ａ、ＣＡ＝ｂ、ＡＢ＝ｃ とし、∠ＰＡＢ＝θと
おくと、
ｔａｎθ＝４Ｓ/（ａ2＋ｂ2＋ｃ2）
が成り立つ。実際に、余弦定理より、
ＰＢ2＝ＰＡ2＋ＡＢ2−２ＰＡ・ＡＢｃｏｓθ
ＰＣ2＝ＰＢ2＋ＢＣ2−２ＰＢ・ＢＣｃｏｓθ
ＰＡ2＝ＰＣ2＋ＣＡ2−２ＰＣ・ＣＡｃｏｓθ
これらを辺々加えて、 ａ2＋ｂ2＋ｃ2＝２（ＰＢ・ａ＋ＰＣ・ｂ＋ＰＡ・ｃ）ｃｏｓθ
＝２（ＰＢ・ａ＋ＰＣ・ｂ＋ＰＡ・ｃ）ｓｉｎθ/ｔａｎθ
＝４Ｓ/ｔａｎθ
よって、 ｔａｎθ＝４Ｓ/（ａ2＋ｂ2＋ｃ2） が成り立つ。
ヘロンの公式より、 ２ｓ＝ａ＋ｂ＋ｃ に対して、
１６Ｓ2＝２ｓ（２ｓ−２ａ）（２ｓ−２ｂ）（２ｓ−２ｃ）
＝（ａ＋ｂ＋ｃ）（−ａ＋ｂ＋ｃ）（ａ−ｂ＋ｃ）（ａ＋ｂ−ｃ）
＝｛（ｂ＋ｃ）2−ａ2｝｛ａ2−（ｂ−ｃ）2｝
＝−ａ4＋｛（ｂ＋ｃ）2＋（ｂ−ｃ）2｝ａ2−（ｂ＋ｃ）2（ｂ−ｃ）2
＝−ａ4＋２（ｂ2＋ｃ2）ａ2−ｂ4＋２ｂ2ｃ2−ｃ4
＝−ａ4−ｂ4−ｃ4＋２ａ2ｂ2＋＋２ｂ2ｃ2＋２ｃ2ａ2
＝（ａ2＋ｂ2＋ｃ2）2−２（ａ4＋ｂ4＋ｃ4）
ｔａｎθ＝４Ｓ/（ａ2＋ｂ2＋ｃ2）≦１/
を示すためには、４８Ｓ2≦（ａ2＋ｂ2＋ｃ2）2 を示せばよい。
ヘロンの公式 １６Ｓ2＝（ａ2＋ｂ2＋ｃ2）2−２（ａ4＋ｂ4＋ｃ4） を代入して、
３｛（ａ2＋ｂ2＋ｃ2）2−２（ａ4＋ｂ4＋ｃ4）｝≦（ａ2＋ｂ2＋ｃ2）2 が言えればよい。
よって、 （ａ2＋ｂ2＋ｃ2）2≦３（ａ4＋ｂ4＋ｃ4） が言えればよいが、この不等式は、
ａ2ｂ2＋ｂ2ｃ2＋ｃ2ａ2≦ａ4＋ｂ4＋ｃ4
が言えることから成り立つ。 （別証終）
（コメント） いつも見慣れた形のヘロンの公式ではなく、新しい視点から見たヘロンの公式も
魅力的ですね！
（追記） 平成２６年１１月２２日付け
１年ぶりに筑波大学附属駒場高校を訪れた。校内を歩いていると、廊下に展示してあるパ
ネルが目に留まった。
「防犯カメラの設置問題」 （２年 富士晃成）
以前、富士晃成さんの展示パネルから、この頁を起こし紹介した。今回の展示パネルは、
平成２６年８月２３日にエルおおさかで行われたマスフェスタ（全国数学生徒研究発表会」で
発表されたもののようだ。
問 題
視界の角度がｘ°の防犯カメラ３台を三角形の各頂点に配置する。ただし、視界の境界の
一方を各辺に一致させるものとする。
任意の鋭角三角形に対して、その三角形の内部をすべて監視できるようにしたいとき、ｘ
はどこまで小さくできるか？
問題の趣旨は何となく「ブロカール点」と同じような匂いを感じる。
（解） 円Ｃ1 は、点Ｂで辺ＢＣに接し、円Ｃ2は、点Ａで辺ＡＢに接する。このとき、
接弦定理により、 ∠ＰＡＢ＝∠ＰＢＣ＝∠ＰＣＡ が成り立つ。
△ＡＢＣに対して、∠ＰＡＢ＝∠ＰＢＣ＝∠ＰＣＡ を満たす点が、ブロカール点であり、上
図から、この点は確かに存在する。
∠ＰＡＢ＝θ とおくと、題意を満たすためには、「θ≦ｘ」であることが必要十分である。
ブロカール点の性質から、θ≦３０°なので、防犯カメラの視界 ｘ は、３０°以上である。
（終）
展示パネルにある「θ≦３０°」の証明を見ると、１年前に見た証明の危うさを解消されて
いて改良されたように感じる。
左図において、点Ｘはブロカール点である。
θ≦３０°が成り立つことを示す。
（証明） △ＡＢＣにおいて、ＢＣ＝ａ、ＣＡ＝ｂ、ＡＢ＝ｃ とおく。さらに、ＸＡ＝ｐ、ＸＢ＝ｑ、
ＸＣ＝ｒ とおく。∠ＸＡＢ＝∠ＸＢＣ＝∠ＸＣＡ＝θとし、△ＡＢＣの面積をＳとおく。
余弦定理より、
ＰＢ2＝ＰＡ2＋ＡＢ2−２ＰＡ・ＡＢｃｏｓθ
ＰＣ2＝ＰＢ2＋ＢＣ2−２ＰＢ・ＢＣｃｏｓθ
ＰＡ2＝ＰＣ2＋ＣＡ2−２ＰＣ・ＣＡｃｏｓθ
これらを辺々加えて、 ａ2＋ｂ2＋ｃ2＝２（ＰＢ・ａ＋ＰＣ・ｂ＋ＰＡ・ｃ）ｃｏｓθ
＝２（ＰＢ・ａ＋ＰＣ・ｂ＋ＰＡ・ｃ）ｓｉｎθ/ｔａｎθ
＝４Ｓ/ｔａｎθ
よって、 ｔａｎθ・（ａ2＋ｂ2＋ｃ2）＝４Ｓ が成り立つ。
イェンゼンの不等式より、 （ａ2＋ｂ2＋ｃ2）/３≧｛（ａ＋ｂ＋ｃ）/３｝2 が成り立つ。
また、周長一定の三角形で面積が最大のものは正三角形なので、（→ 参考）
Ｓ≦（
/４）｛（ａ＋ｂ＋ｃ）/３｝2以上から、 ｔａｎθ＝４Ｓ/（ａ2＋ｂ2＋ｃ2）≦１/
より、 θ≦３０° （終）（コメント） 証明が本当にスッキリしましたね！
以下、工事中！