１．整数論の基礎知識 
（１） ガウスの整数
中学・高校で、 ・・・、−２、−１、０、１、２、・・・ を整数と言ってきたが、ここでは、有理
整数と言い換え、
複素数 ａ＋ｂ・ｉ （ａ、ｂ は有理整数 、ｉ は虚数単位）
の形の数を、整数（ガウスの整数）と呼ぶことにする。
この整数は、和・差・積の演算について閉じているが、商については閉じていない。
２つの整数 ｚ 、ｗ （ｗ≠０）について、ある整数 α が存在して、
ｚ＝α・ｗ
が成り立つとき、 ｚ は、ｗ の倍数（ｗ は、ｚ の約数）または、ｚ は ｗ で割り切れるという。
ｗ｜ｚ とも記される。
例 ０＝０・ｗ なので、０ は全ての整数の倍数である。
（１＋２・ｉ）・（３＋４・ｉ）＝−５＋１０・ｉ なので、−５＋１０・ｉ
は、３＋４・ｉ の倍数
複素数では、絶対値 ｜ａ＋ｂ・ｉ｜＝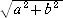
が大活躍するが、整数論では、
Ｎ（ａ＋ｂ・ｉ）＝（ａ＋ｂ・ｉ）・（ａ−ｂ・ｉ）＝ａ2＋ｂ2
が用いられる。これを、整数 ａ＋ｂ・ｉ のノルム（Norm）という。
ｚ＝ａ＋ｂ・ｉ の共役を、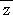
＝ａ−ｂ・ｉ で表せば、 Ｎ（ｚ）＝ｚ・ 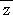＝｜ｚ｜2 なので、ノルム
は、絶対値とほぼ同じ概念といえる。
ノルムＮ（ｚ）は、０以上の整数で、Ｎ（ｚｗ）＝Ｎ（ｚ）・Ｎ（ｗ） 、Ｎ（ｚ/ｗ）＝Ｎ（ｚ）/Ｎ（ｗ）
整数論で絶対値を用いない理由は、多分、根号が煩わしいからだろう。（個人的予想！）
根号を使わないので、
整数 ｚ のノルム Ｎ（ｚ）は、整数 ｚ の倍数
であることが分かる。
このノルムを用いて、最大公約数、最小公倍数が定義される。
最大公約数 ・・・・・ 公約数のうちで、ノルムが最大のもの
最小公倍数 ・・・・・ 公倍数のうちで、ノルムが最小のもの
例 ２ と ２ｉ の最大公約数・最小公倍数を求めよ。
２＝（１＋ｉ）・（１−ｉ） 、２ｉ ＝（１＋ｉ）2 なので、
最大公約数は、１＋ｉ で、最小公倍数は、（１＋ｉ）2・（１−ｉ）＝２＋２・ｉ
ノルムと同様にして、シュプール（Ｓｐｕｒ）（または、トレース（trace））が定義される。
Ｓ（ｚ）＝ｚ＋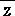
シュプールＳ（ｚ）は、偶数で、Ｓ（ｚ＋ｗ）＝Ｓ（ｚ）＋Ｓ（ｗ）
例 ｚ＝３＋２ｉ のノルム Ｎ（ｚ）＝（３＋２ｉ）・（３−２ｉ）＝１３
シュプール Ｓ（ｚ）＝（３＋２ｉ）＋（３−２ｉ）＝６
有理整数では、「１」という数が重要であった。有理整数の群としては単位元であったし、数
直線では、数０と数１の間の長さを単位として、他の数の配置を求めたりもした。
また、有理整数 １ は、全ての有理整数の約数という性質も持っていた。ここでは、この性
質に注目して、単数という概念が理解される。
全ての整数の約数となる整数を、単数という。
１＝１＋０・ｉ も整数なので、明らかに、単数 ε は、１ の約数である。よって、ある整数 δ
が存在して、１＝ε・δ が成り立つ。
よって、 Ｎ（ε・δ）＝Ｎ（ε）・Ｎ（δ）＝Ｎ（１）＝１ より、 Ｎ（ε）＝１
したがって、 ε＝ａ＋ｂ・ｉ とおくと、 ａ2＋ｂ2＝１ なので、
（ａ ， ｂ）＝（１ ， ０）、（−１ ， ０）、（０ ， １）、（０ ， −１）
以上から、ガウスの整数における単数は、１、−１、ｉ 、−ｉ の４個であることが分かる。
これらは丁度、ガウス平面において、原点中心、半径 １ の円と各軸との交点である。
有理整数では、素数という概念が重要であった。素因数分解により、有理整数の構造・
性質が明らかとなった。ガウスの整数においても、同様の議論が可能である。そのために、
ガウスの整数における素数を定義しなければならない。
整数 ｚ に対して、単数 １、−１、ｉ、−ｉ および、ｚ、−ｚ、ｉｚ、−ｉｚ
は、自明な約数で、有理
整数における、１と−１ と同様に因数としては、度外視して考えるものとする。
例 ６＝１・６ とは普通考えない。 ６＝２・３ と因数に分解する方が自然であろう。
整数 ｚ に対して、自明でない約数を、真の約数という。
このとき、整数 ｚ が、０でも単数でもなく、かつ、真の約数を持たないとき、素数であると
いう。
例 ２ は素数でない。 実際に、２＝（１＋ｉ）・（１−ｉ） で、真の約数 １＋ｉ 、１−ｉ を持つ。
例 ３ は素数である。
実際に、３ が素数でないとすると、真の約数 ｚ 、ｗ が存在して、３＝ｚ・ｗ と書ける。
このとき、Ｎ（３）＝Ｎ（ｚ）Ｎ（ｗ） より、Ｎ（ｚ）Ｎ（ｗ）＝９ である。Ｎ（ｚ）、Ｎ（ｗ）＞１ なので、
Ｎ（ｚ）＝Ｎ（ｗ）＝３ となる。ところが、この式を満たす整数 ｚ は存在しない。
もし、ｚ＝ａ＋ｂ・ｉ （ａ、ｂ は有理整数）が存在するとすると、ａ2＋ｂ2＝３ とならなければな
らないが、それは不可能。
なぜなら、 ａ2＋ｂ2≡３ （ｍｏｄ ４） において、左辺は、０，１，２ の場合しかないので、
矛盾である。
よって、３ は素数である。
有理整数の世界で素数であったものが、素数だったり、そうでなかったりと、ガウスの整
数の世界は、今までの有理整数の世界とは若干違うようである。そこがまた数学の面白さ
なのだろう。
整数が素数かどうかを判断する公式として、次の定理が知られている。
定理 整数 ｚ のノルム Ｎ（ｚ） が素数ならば、整数 ｚ は素数である。
（証明） 整数 ｚ が素数でないとすると、真の約数 α 、β が存在して、ｚ＝α・β と書ける。
このとき、Ｎ（ｚ）＝Ｎ（α）Ｎ（β） が素数より、Ｎ（α） または Ｎ（β） の何れかが １ である。
しかるに、α 、β は、真の約数なので、Ｎ（ｚ）、Ｎ（ｗ）＞１ でなければならない。
これは矛盾である。よって、整数 ｚ は素数である。 （証終）
（注） Ｎ（３）＝９ が素数でないのに、３が素数であるように、上記の定理の逆は成立しない。
ガウスの整数で、素数といわれるものをいくつか調べておこう。
例 １＋ｉ ・・・ Ｎ（１＋ｉ）＝２ は素数より。
１−ｉ は、１−ｉ ＝（−ｉ）・（１＋ｉ） により得られる。
一般に、単数 ε を用いて、ｚ＝ε・ｗ と書けるとき、ｚ と ｗ は同伴数であるという。
整除の問題（割り切れる・割り切れない）において、整数を同伴数に置き換えても何ら影響
はないので、同伴数を同一の因数とみなしてもよい。
したがって、２＝（１＋ｉ）・（１−ｉ）＝（−ｉ）・（１＋ｉ）2 において、２ という数は、２つの方法で
素因数分解できるように見えるが、この約束により、２ という数は、素数 １＋ｉ の２乗に素因
数分解されることが分かる。
ａ 、ｂ＞０ のとき、
ａ−ｂ・ｉ ＝（−ｉ）・（ｂ＋ａ・ｉ）、−ａ＋ｂ・ｉ ＝ｉ・（ｂ＋ａ・ｉ）、−ａ−ｂ・ｉ ＝（−１）・（ａ＋ｂ・ｉ）
なので、以下では、 ａ＋ｂ・ｉ （ａ 、ｂ＞０） の形の整数について調べることにする。
例 ２＋ｉ ・・・ Ｎ（２＋ｉ）＝５ は素数より。
例 ３＋２・ｉ ・・・ Ｎ（３＋２・ｉ）＝１３ は素数より。
３＋ｉ は素数でない。実際に、３＋ｉ ＝（１＋ｉ）・（２−ｉ）より。
例 ４＋ｉ ・・・ Ｎ（４＋ｉ）＝１７ は素数より。
４＋２・ｉ は素数でない。実際に、４＋２・ｉ ＝２・（２＋ｉ）より。
４＋３・ｉ は素数でない。実際に、４＋３・ｉ ＝（１＋２・ｉ）・（２−ｉ）より。
例 ５＋２・ｉ ・・・ Ｎ（５＋２・ｉ）＝２９ は素数より。
５＋ｉ は素数でない。実際に、５＋ｉ ＝（１＋ｉ）・（３−２・ｉ）より。
５＋３・ｉ は素数でない。実際に、５＋３・ｉ ＝（１＋ｉ）・（４−ｉ）より。
例 ５＋４・ｉ ・・・ Ｎ（５＋４・ｉ）＝４１ は素数より。
素数の分布の様子を図示すれば下図のようになる。（同色は、同伴数）
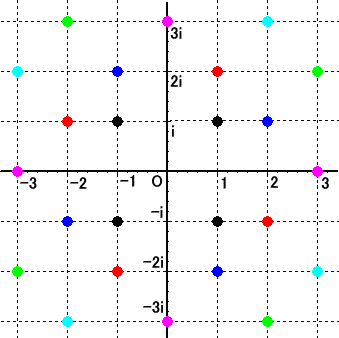
（参考） 西山 豊 著 人とヒトデとサッカーボール （三省堂）の１９７頁に、この素数の分布
の様子を表した図が掲載されている。上図では分かりにくいが、きれいな幾何学模様で、
１９８８年ハンガリーで開催されたＩＣＭＥ（国際数学教育研究会）で、イギリスのグループ
が素数の分布を表す模様のスカーフを展示したそうである。
整数 ｚ に対して、素数 α 、β 、・・・ があって、 ｚ＝α×β×・・・ と積の形にかけるとき、
整数 ｚ は、素因数に分解されるという。
ここで、素因数は有限個しかない。
実際に、整数 Ｎ（α）、Ｎ（β）、・・・ は、１ より大きい整数で、Ｎ（ｚ） は有限の値より明らか。
今までの話から、整数 ｚ がいくつかの素因数に必ず分解できるということは理解できるだ
ろう。しかし、素因数分解において、大切なことは、その分解の一意性にある。もし、一意性
が成立すれば、有理整数における性質が、ガウスの整数においても同様に成り立つことに
なる。
一意性を証明するためには、いくつかの準備が必要となる。まずは、整除の定理から。
定理 任意の整数 ｚ 、ｗ （ｗ≠０） に対して、
ｚ ＝ ｗ・α＋β （ Ｎ（β）＜Ｎ（ｗ） ） を満たす整数 α 、β が存在する。
（証明） 任意の整数 ｚ 、ｗ （ｗ≠０） に対して、複素数 ξ＝ｚ/ｗ が定義される。
 |
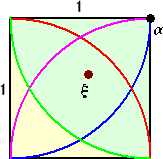ガウス平面（複素数平面）において、左図からも明らかなよう
に、ある整数 α が存在して、 Ｎ（ξ−α）＜１ とできる。
そこで、 β＝ｚ−ｗ・α とおくと、β は整数で、
Ｎ（β）＝Ｎ（ｚ−ｗ・α）＝Ｎ（ｗ・（ξ−α））
＝Ｎ（ｗ）・Ｎ（ξ−α）＜Ｎ（ｗ）
|
| 以上から、ｚ ＝ ｗ・α＋β （Ｎ（β）＜Ｎ（ｗ） ） を満たす整数 α 、β が存在する。 （証終） |
この定理により、ガウスの整数においても、ユークリッドの互除法を行うことができる。
任意の整数 ｚ 、ｗ （ｗ≠０） に対して、ｚ ＝ ｗ・α＋β （ Ｎ（β）＜Ｎ（ｗ） ）を満たす整数
α 、β が存在する。 もし、β ＝ ０ なら、ｚ は、ｗ で割り切れる。
β ≠ ０ のとき、ｗ ＝ β・γ’＋γ （Ｎ（γ）＜Ｎ（β） ）を満たす整数 γ 、γ’ が存在する。
このような操作を続けると、ノルムは、０ 以上の整数なので、結局最後は、δ ＝ ε・ζ’
を満たす整数 ζ’ が存在する。（つまり、ζ＝０ で最後は割り切れる！）
このとき、ε は、整数 ｚ 、ｗ の公約数である。逆に、整数 ｚ 、ｗ の公約数は、ε の約数
でもあるので、ε は、整数 ｚ 、ｗ の最大公約数であるといえる。
通常、最大公約数 ε は、整数 ｚ 、ｗ を用いて、 ε ＝ （ ｚ ， ｗ ） と書かれる。
以上の話を整理すると、有理整数の場合と同様に、次の定理が成り立つ。
定理 任意の整数 ｚ 、ｗ （ｗ≠０） に対して、 α・ｚ ＋ β・ｗ ＝ （ ｚ ，
ｗ ）
を満たす整数 α 、β が存在する。
（証明） ユークリッドの互除法から明らか。 （証終）
例 ２つの整数 ７＋４・ｉ 、９＋２・ｉ の最大公約数を求めてみよう。
９＋２・ｉ ＝ （７＋４・ｉ）・１＋２−２・ｉ 、７＋４・ｉ ＝ （２−２・ｉ）・（１＋３・ｉ）−1
２−２・ｉ ＝ （−1）・（−２＋２・ｉ）
よって、最大公約数は、−1 である。
このように、単数が最大公約数であるとき、２つの整数は、互いに素であるという。
例 ２つの整数 ３−ｉ 、４−３・ｉ の最大公約数を求めてみよう。
４−３・ｉ ＝ （３−ｉ）・１＋１−２・ｉ 、３−ｉ ＝ （１−２・ｉ）・（１＋ｉ）
よって、最大公約数は、１−２・ｉ である。
＃このとき、１・［ ４−３・ｉ ］＋（−1）・［ ３−ｉ ］ ＝ １−２・ｉ が成り立つ。
いよいよ、素因数分解の一意性を証明する準備ができたようだ。
補題 整数 ｚ 、ｗ が互いに素であるとき、
ｚ・α が ｗ で割り切れれば、α は、ｗ で割り切れる。
（証明） 整数 ｚ 、ｗ が互いに素なので、ｘ・ｚ ＋ ｙ・ｗ ＝ ε （ε は単数） となる整数
ｘ 、ｙ が存在する。このとき、ε・α ＝ ｘ・ｚ・α ＋ ｙ・ｗ・α は、ｗ で割り切れる。
すなわち、α は、ｗ で割り切れる。 （証終）
定理 任意の整数 ｚ は、一意に素因数分解される。
（証明） 整数 ｚ が、２通りに素因数分解されるものと仮定する。
ｚ ＝ α1×α2× ・・・＝β1×β2× ・・・
このとき、補題により、単数 ε1 、ε2 、・・・ として、
α1×α2× ・・・ ＝ （ε1×ε2×・・・）・（β1×β2× ・・・）
と書ける。
よって、２通りの素因数分解は、単数の差しかないので、一意であるとしてよい。 （証終）
上記で、ガウスの整数における素数の例をいくつか挙げたが、一般に、素数は、どのよう
な形をしているのだろうか？これも、大いに興味のあるところである。
以下で、ガウスの整数における素数と区別するために、有理整数における素数を、有理
素数と呼ぶことにする。
いま、整数 ｚ を素数として、その性質を見ていこう。
ｚ で割り切れる正の有理整数のうちで最小のものを、ｐ とする。このような
ｐ は必ず存在
する。（例えば、Ｎ（ｚ）は、ｚ で割り切れる。）
このとき、 ｐ は、有理素数である。
実際に、 ｚ は素数で単数ではないから、ｐ ＞ １ で、ｐ が有理素数でないとすると、
ｐ ＝ α・β （ ｐ＞α＞１ 、ｐ＞β＞１ ） となる有理整数 α 、β が存在し、
α または β は、ｚ で割り切れる。
これは、ｐ の最小性に矛盾する。 よって、 ｐ は、有理素数である。
したがって、素数 ｚ は、有理素数 ｐ の約数となる。そこで、 ｐ ＝ ｚ・γ とおける。
このとき、 Ｎ（ｐ）＝Ｎ（ｚ）・Ｎ（γ） で、Ｎ（ｐ）＝ｐ2 なので、Ｎ（ｚ）＝ｐ または Ｎ（ｚ）＝ｐ2
となる。 Ｎ（ｚ）＝ｐ のとき、 ｚ＝ａ＋ｂ・ｉ とおくと、 ａ2＋ｂ2＝ｐ より、 ｐ＝ｚ・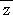
Ｎ（ｚ）＝ｐ2 のとき、 Ｎ（γ）＝１ で、γ は単数で、ｚ は、ｐ と同伴数となる。
このとき、ｐ は、ガウスの整数としても素数となり、Ｎ（ｚ）＝ｐ のときのような ｐ の分解は
不可能である。
以上から、
素数 ｚ＝ａ＋ｂ・ｉ と有理素数 ｐ について、
Ｎ（ｚ）＝ｐ のとき、 ｐ は素数でなく、 ｐ＝ｚ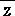＝ａ2＋ｂ2 と分解される。（→参考）
Ｎ（ｚ）＝ｐ2 のとき、 ｐ は素数で、ａ2＋ｂ2＝ｐ を満たす ａ 、ｂ は存在しない。
したがって、有理素数 ｐ について、方程式 ｘ2＋ｙ2＝ｐ の解を吟味することにより、素
数が求められる。
例 ｐ＝２ のとき、 方程式 ｘ2＋ｙ2 ＝ ２ の解は、
（ ｘ ， ｙ ）＝（ １ ， １ ）（ １ ， −１ ）（ −１ ， １ ）（ −１ ， −１ ）
よって、 ｐ＝２ は素数でなく、素数 ｚ は、１＋ｉ 、１−ｉ 、−１＋ｉ 、−１−ｉ となる。
このうち、１−ｉ 、−１＋ｉ 、−１−ｉ は、すべて １＋ｉ の同伴数である。
実際に、 １−ｉ ＝ （−ｉ）・（１＋ｉ）、−１＋ｉ ＝ ｉ ・（１＋ｉ）、−１−ｉ ＝ （−１）・(１＋ｉ）
方程式 ｘ2＋ｙ2 ＝ ｐ （ｐ≠２）の解があるとする。 ｐ は、奇数なので、ｘ または ｙ のうち
一方は偶数、他方は奇数である。このとき、ｐ は、４で割って、１余る数である。
このことは、４で割って、３余る有理素数 ｐ に対して、ａ2＋ｂ2＝ｐ を満たす ａ、ｂ が存在
しないことを意味し、
４で割って３余る有理素数 ｐ は、ガウスの整数としても素数
となる。
例 有理素数 ３ は、素数である。（→ 参考）
例 有理素数 ７ は、素数である。
例 有理素数 １１ は、素数である。
ｐ が、４で割って、１余る数のとき、方程式 ｘ2＋ｙ2 ＝ ｐ は、どのような解を持つのだろう
か？（→ Ｌｅｇｅｎｄｒｅ の記号、指数等について既に理解されている方は、こちらへジャンプ）
ここで、整数論では大切な記号 Ｌｅｇｅｎｄｒｅ の記号を復習しておこう。
例 方程式 Ｘ2≡１ （ｍｏｄ ３） は、Ｘ＝３ｎ±１ （ｎ は整数）という形の解を持つが、
方程式 Ｘ2≡２ （ｍｏｄ ３） は、決して解を持たない。
一般に、ｐ を２以外の素数として、方程式 Ｘ2≡ａ （ｍｏｄ ｐ） が
解を持つとき、 ａ を ｐ の平方剰余
解を持たないとき、ａ を ｐ の平方非剰余
という。
例 ３で割った余りは、０、１、２ であるが、その余りを平方したものを３で割った余りは、０、
１ の場合しか起こらない。
このとき、０ と １ は、３ の平方剰余となり、２ は、３ の平方非剰余となる。
例 ７で割った余りは、０、１、２、３、４、５、６ であるが、その余りを平方したものを７で割った
余りは、０、１、２、４ の場合しか起こらない。
このとき、０ と １ と ２ と ４ は、７ の平方剰余となり、３ と ５ と ６ は、７ の平方非剰余と
なる。
０2≡０ （ｍｏｄ ７） 、１2≡６2≡１ （ｍｏｄ ７） 、３2≡４2≡２ （ｍｏｄ ７）、
２2≡５2≡４ （ｍｏｄ ７）
ａ が、ｐ で割り切れないとき、ａ が平方剰余であるか、平方非剰余であるかを次のような
記号を使って表す。
|
平方剰余のときは、 |
 |
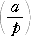＝１ |
|
平方非剰余のときは、 |
|
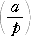＝−1 |
この記号を、Ｌｅｇｅｎｄｒｅ の記号という。
紙面の都合上、以下では、Ｌｅｇｅｎｄｒｅ の記号を、（ａ/ｐ） で表すことにする。
例 （１/３）＝１ 、（２/３）＝−1
ＧＡＩ さんからのコメントです。（平成２４年３月８日付け）
平方剰余の法則と言って、なにやら直感では何を言おうとしているのか掴み難い式で表現
されているのを見ることがあり、よく分からないと言うのが実感です。ある本で、この法則を次
のような表現で解説してある文章があったので、メモしていました。このことと、なにか関係が
ありますか？
表現：
ｐとｑが奇素数で、どちらでも 4ｋ-1 という形でなければ、ｑ≡ｙ2 (ｍｏｄ ｐ) が解を持つと
きに限って、方程式 ｐ≡ｘ2 (ｍｏｄ ｐ) は解を持つ。
また、ｐとｑのどちらかが、4ｋ-1という形であれば、どちらか一方の方程式は解を持ち、もう
一方の方程式は解を持たない。
これでもややこしい解説ではあるのですが、ただ数式で書いてあるよりはイメージが取り易
い気はします。平方剰余の解釈として、これでいいのでしょうか？
空舟さんからのコメントです。（平成２４年３月８日付け）
まさにそれです。個人的には「平方剰余の相互法則」のバニラとチョコレートの解説がすご
く具体的だと思います。
ただし、その表現だとちょっと違いますね。どちらかがバニラ 4N+1 型のとき、解を持つかど
うか一致、両方がチョコレート 4N+3 型の時、不一致 です。
さて、指数という概念を理解するために、フェルマーの定理を確認しておく。
フェルマーの定理 ｐ が有理素数で、ａ が ｐ とは互いに素な自然数とするとき、
ａｐ−1 ≡ １ （ｍｏｄ ｐ）
（証明） ２項定理より、 （ｍ＋ｎ）ｐ≡ｍｐ＋ｎｐ （ｍｏｄ ｐ） は明らかであろう。
これを一般化して、 （ｍ＋・・・＋ｎ）ｐ≡ｍｐ＋・・・＋ｎｐ （ｍｏｄ ｐ） が成り立つ。
ｍ＝・・・＝ｎ＝１ （ａ 個）とすれば、 ａｐ≡ａ （ｍｏｄ ｐ） である。
ここで、 ａ は ｐ とは互いに素な自然数なので、 ａｐ−1≡１ （ｍｏｄ ｐ） （証終）
（追記） 平成２２年３月２２日付け
２０１０年度入試の大阪大学 後期 理系 で、上記のフェルマーの定理の証明を問う問題
が出題された。
ｐ は素数、ｒ は正の整数とする。以下の問いに答えよ。
（１） ｘ1、ｘ2、・・・、ｘｒ についての式 （ｘ1＋ｘ2＋・・・＋ｘｒ）ｐ を展開したときの単項式
ｘ1ｐ1ｘ2ｐ2・・・ｘｒｐｒ の係数を求めよ。ここで、ｐ1、ｐ2、・・・、ｐｒ は、０または正の整数で、
ｐ1＋ｐ2＋・・・＋ｐｒ＝ｐ を満たすとする。
（２） ｘ1、ｘ2、・・・、ｘｒ が正の整数のとき、（ｘ1＋ｘ2＋・・・＋ｘｒ）ｐ−（ｘ1ｐ＋ｘ2ｐ＋・・・＋ｘｒｐ）
は、ｐ で割り切れることを示せ。
（３） ｒ は、ｐ で割り切れないとする。このとき、 ｒｐ-1−１ は、ｐ で割り切れることを示せ。
（コメント） （１）（２）については、多項定理から明らかだろう。上記の証明に倣う形で、小問
（１）（２）が配置されている。したがって、（３）については、上記の証明と同様に、
ｘ1＝ｘ2＝・・・＝ｘｒ＝１ とすればよい。
フェルマーの定理より、方程式 ａｘ≡１ （ｍｏｄ ｐ）を満たす自然数解が存在するので、
そのうちの最小の自然数解を、ｅ とすると、 ｐ−1 は、ｅ で割り切れる。
さらに、ｅ の最小性から、 ａ0 、ａ1 、ａ2 、・・・、ａｅ−1 は、ｐ を法として合同にはなり
えない。
特に、ｅ＝ｐ−１ のとき、 ａ を ｐ を法としての原始根（または、ｐ の原始根）という。
例 ｐ＝７ のとき、
１ に対する ｅ ＝ １ 、２ に対する ｅ ＝ ３ 、３ に対する ｅ ＝ ６ 、
４ に対する ｅ ＝ ３ 、５ に対する ｅ ＝ ６ 、６ に対する ｅ ＝ ２
以上から、７の原始根は、２個あり、 ３ と ５ である。
ここで、自然数 １、２、３、・・・、ｎ の中で、ｎ と互いに素な数の個数は、φ（ｎ）で表される。
この関数を、オイラーの関数という。
例 φ（１）＝１、φ（２）＝１、φ（３）＝２、φ（４）＝２、φ（５）＝４、φ（６）＝２、φ（７）＝６
オイラーの関数について、次の性質が成り立つ。
（１） 有理素数 ｐ に対して、 φ（ｐ）＝ｐ−１ 特に、φ（ｐｎ）＝ｐｎ−ｐｎ−1
（２） ａ と ｂ が互いに素ならば、 φ（ａｂ）＝φ（ａ）φ（ｂ）
（証明） （１）は、明らかであろう。
（２）は、次のように示される。
ａ より小さい数で、ａ と互いに素な数は、φ（ａ）個あり、その一つを、α とおく。
このとき、 ｂ 個の数 α、α＋ａ、α＋２ａ、・・・、α＋（ｂ−1）ａ を考える。
これらは、何れも ｂ を法として合同でない。
したがって、ａｂ と互いに素な数は全部で、φ（ａ）×φ（ｂ）個あるので、φ（ａｂ）＝φ（ａ）φ（ｂ）
が成り立つ。 （証終）
例 φ（２）＝２−１＝１ 、φ（３）＝３−１＝２ 、φ（４）＝φ（２2）＝４−２＝２、
φ（６）＝φ（２）φ（３）＝１×２＝２
オイラーの関数 φ（ｎ） を用いると、上記で述べたことは、次のようにも言い換えることが
できる。
ｐ が有理素数で、ａ が ｐ とは互いに素な自然数とするとき、
ａφ（ｐ） ≡ １ （ｍｏｄ ｐ）
この合同式を満たすφ（ｎ）が最小のものであるとき、ａ を、ｐ の原始根という。
もし、原始根が存在すれば、それは、φ（ｐ−1）個存在する。
原始根の一つを、ｇ （ｇ≠１）とすれば、１、ｇ、ｇ2、ｇ3、・・・、ｇｐ−2 は、互いに合同で
ない ｐ−１ 個の数で、いずれも ｐ では割り切れない。
いま、ａ を ｐ とは互いに素な任意の自然数とするとき、上記のことから、
ｇｅ ≡ ａ （ｍｏｄ ｐ） となる ｅ （０≦ ｅ ＜ｐ−1 ）がただ一つ存在する。このとき、
ｅ ＝ ｉｎｄｇ（ａ）
で表し、原始根 ｇ を底とする ａ の指数（ｉｎｄｅｘ）という。
（注） ｇｅ ≡ ａ （ｍｏｄ ｐ）、ｇｆ ≡ ａ （ｍｏｄ ｐ）ならば、ｇｅ−ｆ ≡ １ （ｍｏｄ ｐ）
よって、ｅ−ｆ は、ｐ−１で割り切れるので、 ｅ ≡ f （ｍｏｄ ｐ−１）
したがって、上記では、０≦ ｅ ＜ｐ−1 と限定したが、ｐ−１ を法として考えれば、
ａ の指数は、一定であるといえる。故に、
ａ ≡ ｂ （ｍｏｄ ｐ） ⇔ ｉｎｄｇ（ａ） ≡ ｉｎｄｇ（ｂ） （ｍｏｄ ｐ−１）
が成り立つ。
例 ７ の原始根の一つ ３ について、３ を底とする指数表を作ってみよう。
３0 ≡ １ （ｍｏｄ ７）、３1 ≡ ３ （ｍｏｄ ７）、３2 ≡ ２ （ｍｏｄ ７）、
３3 ≡ ６ （ｍｏｄ ７）、３4 ≡ ４ （ｍｏｄ ７）、３5 ≡ ５ （ｍｏｄ ７）
以上から、
|
| ａ |
１ |
２ |
３ |
４ |
５ |
６ |
| 指数 |
０ |
２ |
１ |
４ |
５ |
３ |
|
また、上記指数表を眺めていると、
ａ の値における「 ２ かける ３ ＝ ６ 」が、指数では、「 ２＋１ ＝ ６」が対応し、
ａ の値における「 ４ かける ５ ＝ ２０ 」が、指数では、「 ４＋５ ≡ ３（ｍｏｄ ６）」が対応
していることが分かる。
このことから、指数には、対数に似た性質があることに気づかされる。すなわち、
ｐ−１ を法として、ｉｎｄｇ（ａ×ｂ） ≡ ｉｎｄｇ（ａ） ＋ ｉｎｄｇ（ｂ）
ｉｎｄｇ（ａｎ） ≡ ｎ×ｉｎｄｇ（ａ）
証明は、明らかであろう。
上記の指数表を用いて、いろいろ計算してみよう。
（１） 指数計算・・・・・
２０ ≡ ６ （ｍｏｄ ７） なので、ｉｎｄ3（２０） ≡ ｉｎｄ3（６） ＝ ３ （ｍｏｄ ６）
（２） 指数方程式・・・・・
ｉｎｄ3（Ｘ）≡ ２ （ｍｏｄ ６） とすれば、上記表より、ｉｎｄ3（Ｘ） ≡ ｉｎｄ3（２） （ｍｏｄ ６）
よって、 Ｘ ≡ ２ （ｍｏｄ ７）
（３） １次方程式・・・・・・
４Ｘ ≡ ３ （ｍｏｄ ７） において、ｉｎｄ3（４Ｘ） ≡ ｉｎｄ3（３） （ｍｏｄ ６） より、
ｉｎｄ3（４） ＋ ｉｎｄ3（Ｘ） ≡ ｉｎｄ3（３） （ｍｏｄ ６）
よって、 ４ ＋ ｉｎｄ3（Ｘ） ≡ １ （ｍｏｄ ６） なので、ｉｎｄ3（Ｘ） ≡ −３ ≡ ３ （ｍｏｄ ６）
したがって、 Ｘ ≡ ６ （ｍｏｄ ７）
（４） 方程式・・・・・・
Ｘ3 ≡ ４ （ｍｏｄ ７）において、ｉｎｄ3（Ｘ3） ≡ ｉｎｄ3（４） （ｍｏｄ ６）
よって、 ３×ｉｎｄ3（Ｘ） ≡ ４ （ｍｏｄ ６）
上式を満たす ｉｎｄ3（Ｘ） の値はないので、解なし。
上記の（４）に関連して、次の定理が知られている。
定理Ａ ｐ は有理素数とし、ａ は ｐ で割り切れないものとする。
Ｘｎ ≡ ａ （ｍｏｄ ｐ） が解を持つための必要十分条件は、
（ｎ ，ｐ−１）＝ｄ として、 ｉｎｄｇ（ａ） ≡ ０ （ｍｏｄ ｄ）
（証明） ｉｎｄｇ（Ｘｎ） ≡ ｉｎｄｇ（ａ） （ｍｏｄ ｐ−１） より、
ｎ × ｉｎｄｇ（Ｘ） ≡ ｉｎｄｇ（ａ） （ｍｏｄ ｐ−１）
この式を言い換えれば、解 ｉｎｄｇ（Ｘ） が存在するためには、不定方程式
ｎ × Ｍ ＋ （ｐ−１） × Ｎ ＝ ｉｎｄｇ（ａ）
を満たす整数 Ｍ（＝ ｉｎｄｇ（Ｘ））、Ｎ が存在することが必要十分である。
そのためには、互除法の理論により、 ｎ と ｐ−１ の最大公約数 ｄ により
ｉｎｄｇ（ａ） が割り切れることが必要十分である。
よって、ｉｎｄｇ（ａ） ≡ ０ （ｍｏｄ ｄ） でなければならない。 （証終）
（コメント） 上記の定理に照らせば、（４）では、ｉｎｄ3（４） ＝ ４ で、（３ ，６）＝３ から
ｉｎｄ3（４） ≡ ０ （ｍｏｄ ３）が成り立たないので、解は存在し得ないことが分かる。
・・・空舟さんより誤りの指摘を受け、修正済み（Ｈ24.2.29）
（５） ２次方程式・・・・・
２Ｘ2−３Ｘ＋５ ≡ ０ （ｍｏｄ ７）において、両辺を４倍して、８Ｘ2−１２Ｘ＋２０ ≡ ０ （ｍｏｄ ７）
すなわち、Ｘ2＋２Ｘ−１ ≡ ０ （ｍｏｄ ７） となる。このとき、（Ｘ＋１）2 ≡ ２ （ｍｏｄ ７）
ここで、（２ ，６）＝２ で、ｉｎｄ3（２） ≡ ０ （ｍｏｄ ２）なので、解が存在する。
ｉｎｄ3（（Ｘ＋１）2） ≡ ｉｎｄ3（２） （ｍｏｄ ６） より、２・ｉｎｄ3（Ｘ＋１） ≡ ２ （ｍｏｄ ６）
上式を満たす ｉｎｄ3（Ｘ＋１） の値は、ｉｎｄ3（Ｘ＋１） ≡ １ 、４ （ｍｏｄ ６）
したがって、 Ｘ＋１ ≡ ３ 、４ （ｍｏｄ ７） すなわち、Ｘ ≡ ２ 、３ （ｍｏｄ ７）
（６） 累乗計算・・・・・
Ｘ ≡ ３100 （ｍｏｄ ７）において、
ｉｎｄ3（Ｘ） ≡ ｉｎｄ3（３100）≡ １００×ｉｎｄ3（３） ≡ １００ ≡ ４ （ｍｏｄ ６）
よって、 Ｘ ≡ ４ （ｍｏｄ ７）
（７） 指数方程式・・・・・
４ｘ ≡ ３ （ｍｏｄ ７）において、ｉｎｄ3（４ｘ） ≡ ｉｎｄ3（３） （ｍｏｄ ６） すなわち、
Ｘ・ｉｎｄ3（４） ≡ ｉｎｄ3（３） （ｍｏｄ ６） より、４・Ｘ ≡ １ （ｍｏｄ ６）
ところが、（４ ，６）＝２ で、１を割れないから、この方程式、すなわち、元の方程式には解
は存在しない。
４ｘ ≡ １ （ｍｏｄ ７）において、ｉｎｄ3（４ｘ） ≡ ｉｎｄ3（１） （ｍｏｄ ６） すなわち、
Ｘ・ｉｎｄ3（４） ≡ ｉｎｄ3（１） （ｍｏｄ ６） より、４・Ｘ ≡ ０ （ｍｏｄ ６）
よって、 Ｘ ≡ ３ （ｍｏｄ ６）
（この２つの例からも分かるように、指数方程式は解を持つ場合と持たない場合があるので
要注意である。）
指数に関して、次の事実が知られている。
定理 有理素数 ｐ は、ｐ≠２ とする。このとき、任意の原始根 ｇ に対して、
ｉｎｄｇ（−１） ≡ （ｐ−１）/２ （ｍｏｄ ｐ−１）
（証明） 原始根 ｇ の定義より、 ｇｐ−1 ≡ １ （ｍｏｄ ｐ） が成り立つ。このとき、
ｇｐ−1−１ ≡ (ｇ(ｐ−１)/2−１)(ｇ(ｐ−１)/2＋１) ≡ ０ （ｍｏｄ ｐ） において、
ｇ(ｐ−１)/2−１ ≡ ０ （ｍｏｄ ｐ）とはなり得ないので、
ｇ(ｐ−１)/2＋１ ≡ ０ （ｍｏｄ ｐ） より、 ｇ(ｐ−１)/2 ≡ −１ （ｍｏｄ ｐ）
したがって、 ｉｎｄｇ（−１） ≡ （ｐ−１）/２ （ｍｏｄ ｐ−１） が成り立つ。 （証終）
例 指数表で、ｉｎｄ3（６） ≡ ３ （ｍｏｄ ６） であるが、６ ≡ −１ （ｍｏｄ ７）なので、
確かに、 ｉｎｄ3（−１） ≡ （７−１）/２ （ｍｏｄ ６） が成り立っている。
この定理を用いると、次の定理が得られる。
定理（ウィルソン） 有理素数 ｐ に対して、 （ｐ−１）！≡ −１ （ｍｏｄ ｐ）
（証明） ｐ＝２ のときは、明らかに成り立つので、以下では、ｐ＞２ とする。
原始根 ｇ を用いて、（ｐ−１）！ ≡ ｇ0+1+2+・・・+(p-2) ≡ ｇ(p-2)(p-1)/2 （ｍｏｄ ｐ）
と書ける。上記の定理より、 ｇ(ｐ−１)/2 ≡ −１ （ｍｏｄ ｐ） なので、ｐ＞２ より、
（ｐ−１）！ ≡ （−１）(p-2)≡ （−１）p≡ −１ （ｍｏｄ ｐ） （証終）
単に、この定理を証明するだけだったら、次のようにした方が分かりやすいだろう。
（平成１８年１２月２９日付け 加俊さんに質問されて見直しました！）
（別証） 素数 ｐ が ２ の場合は、明らかに成り立つ。
奇素数 ｐ に対して、フェルマーの定理より、１≦ｋ≦ｐ−１となる任意の整数 ｋ に対して、
ｋｐ−１≡１ （ｍｏｄ ｐ） が成り立つ。
したがって、多項式Ｆ（Ｘ）＝Ｘｐ−１−１ において、
Ｆ（１）≡０ 、 Ｆ（２）≡０ 、・・・、 Ｆ（ｐ−１）≡０ （ｍｏｄ ｐ）
よって、 Ｆ（Ｘ）≡(Ｘ−１)(Ｘ−２)・・・(Ｘ−ｐ＋１) （ｍｏｄ ｐ） と因数分解される。
そこで、Ｘ＝０ を代入すると、 （−１）ｐ−１・（ｐ−１）！≡−１ （ｍｏｄ ｐ）
ｐ は奇数なので、 （−１）ｐ−１＝１
よって、（ｐ−１）！≡−１ （ｍｏｄ ｐ） が成り立つ。 （別証終）
（コメント） ウィルソンの定理は逆も成り立つ。 すなわち、
ウィルソンの定理の逆 （ｐ−１）！ ≡ −１ （ｍｏｄ ｐ） ならば、ｐ は有理素数
（証明） ｐ が有理素数でないとすると、２つの自然数 ｍ 、ｎ （２ ≦ ｍ
、ｎ ＜ ｐ）を用いて、
ｐ ＝ ｍｎ と書ける。このとき、ｍ は（ｐ−１）！ の約数で、（ｐ−１）！ ＋１ の約数にはなり
得ないので、ｐ は、（ｐ−１）！ ＋１ の約数になり得ない。
これは、条件に矛盾する。 よって、ｐ は素数でなければならない。 （証終）
（追記） 令和４年６月２５日付け
例 ｐ＝７ のとき、 （ｐ−１）！＝６！＝７２０ ＝１０３×７−１ ≡ −１ （ｍｏｄ ７）
よって、７は有理素数である。
上記の対偶は、
ｐ は有理素数でなければ、（ｐ-1）！≡-1 （ｍｏｄ ｐ） は成り立たない
例 合成数の ｐ＝６ に対して、 （６-1）！＝１２０≡０ （ｍｏｄ ６） である。
合成数の ｐ＝４ に対して、 （４-1）！＝６≡２ （ｍｏｄ ４） である。
合成数の ｐ＝８ に対して、 （８-1）！＝５０４０≡０ （ｍｏｄ ８） である。
上記のように、ウィルソンの定理を考えると、定理そのものが難しく思えるが、次のように
考えれば、ウィルソンの定理自体はごく単純なものである。
例えば、ｍｏｄ １１ において、
２×３×４×５×６×７×８×９
＝（２×６）×（３×４）×（５×９）×（７×８）≡１×１×１×１＝１
なので、 １×２×３×４×５×６×７×８×９×１０≡１０≡−１ となる。
上記では、 ２×６≡１ 、３×４≡１ 、５×９≡１ 、７×８≡１ であることが核心である。
ここで、１１を法とする乗法表を考えてみる。
| |
| ＼ |
１ |
２ |
３ |
４ |
５ |
６ |
７ |
８ |
９ |
１０ |
| １ |
１ |
２ |
３ |
４ |
５ |
６ |
７ |
８ |
９ |
１０ |
| ２ |
２ |
４ |
６ |
８ |
１０ |
１ |
３ |
５ |
７ |
９ |
| ３ |
３ |
６ |
９ |
１ |
４ |
７ |
１０ |
２ |
５ |
８ |
| ４ |
４ |
８ |
１ |
５ |
９ |
２ |
６ |
１０ |
３ |
７ |
| ５ |
５ |
１０ |
４ |
９ |
３ |
８ |
２ |
７ |
１ |
６ |
| ６ |
６ |
１ |
７ |
２ |
８ |
３ |
９ |
４ |
１０ |
５ |
| ７ |
７ |
３ |
１０ |
６ |
２ |
９ |
５ |
１ |
８ |
４ |
| ８ |
８ |
５ |
２ |
１０ |
７ |
４ |
１ |
９ |
６ |
３ |
| ９ |
９ |
７ |
５ |
３ |
１ |
１０ |
８ |
６ |
４ |
２ |
| １０ |
１０ |
９ |
８ |
７ |
６ |
５ |
４ |
３ |
２ |
１ |
|
上記の表には、１〜１０までの数が何らかの順序で並んでいる。特に注意すべきは、全て
の行には必ず１が含まれているという点である。この表から、積が１となる２つの数を必ず見
いだすことが出来る。また、すべての行と列には、１１より小さい数が丁度１回ずつ出現して
もいる。
さらに、１×１と１０×１０を結ぶ対角線上に、１が２度出現するが、それは対角線の両端に
おいてである。
このような性質は、一般の素数 ｐ においても成り立つ。
合成数 ｐ では、このようなことは必ずしも言えない。
例えば、ｐ＝６ のとき、ｐ＝１１ の場合と明らかに異なる様相を示す。
| |
| ＼ |
１ |
２ |
３ |
４ |
５ |
| １ |
１ |
２ |
３ |
４ |
５ |
| ２ |
２ |
４ |
０ |
２ |
４ |
| ３ |
３ |
０ |
３ |
０ |
３ |
| ４ |
４ |
２ |
０ |
４ |
２ |
| ５ |
５ |
４ |
３ |
２ |
１ |
|
このように考えると、ウィルソンの定理は、素数 ｐ の乗算表からごく自然に導かれる結果
であると言える。
ウィルソンの定理は、１７７０年に英国の数学者・法律家のジョン・ウィルソン（1741〜1793）
により発表された。具体例を調べて、正しいことは確信していたが、証明は出来なかった。
証明は、仏の数学者ジョゼフ・ルイス・ラグランジュにより、発表されてまもなくなされた。
ライプニッツは、１００年以上も前に、ウィルソンの定理を知っていたとも言われる。
定理（ライプニッツ） 有理素数 ｐ に対して、 （ｐ−２）！≡ １ （ｍｏｄ ｐ）
（証明） ウィルソンの定理より、
（ｐ−１）！ ≡ （ｐ−１）（ｐ−２）！≡−（ｐ−２）！≡−１ （ｍｏｄ ｐ）
なので、 （ｐ−２）！≡ １ （ｍｏｄ ｐ） が成り立つ。 （証終）
先の定理Ａ において、合同式が解を持つための条件を提示したが、原始根を用いてい
る点が気持ちが悪い。
定理Ａは、次のように言い換えることが出来る。
定理Ｂ ｐ は有理素数とし、ａ は ｐ で割り切れないものとする。
Ｘｎ ≡ ａ （ｍｏｄ ｐ） が解を持つための必要十分条件は、
（ｎ ，ｐ−１）＝ｄ、（ｐ−１）/ｄ＝ｆ として、 ａｆ ≡ １ （ｍｏｄ ｐ）
（証明） 定理Ａ より、 解を持つための必要十分条件は、ｉｎｄｇ（ａ） ≡ ０ （ｍｏｄ ｄ）
よって、 ｉｎｄｇ（ａ） ＝ｄｋ （ｋ は自然数） と書ける。 このとき、定義より、
ｇｄｋ ≡ ａ （ｍｏｄ ｐ） となる。
ここで、両辺を ｆ 乗すれば、 ａｆ ≡ ｇ(p-1)ｋ ≡ １ （ｍｏｄ ｐ）
逆に、ａｆ ≡ １ （ｍｏｄ ｐ）が成り立つとすると、原始根を ｇ として、
ｉｎｄｇ（ａｆ） ≡ ｉｎｄｇ（１） （ｍｏｄ ｐ−１） すなわち、 ｆ ×ｉｎｄｇ（ａ） ≡ ０ （ｍｏｄ ｐ−１）
ここで、 （ｎ ，ｐ−１）＝ｄ なので、 ｐ−１＝ｄｈ とおくと、ｈ×ｉｎｄｇ（ａ） ≡ ０ （ｍｏｄ ｄｈ）
よって、ｉｎｄｇ（ａ） ≡ ０ （ｍｏｄ ｄ） が得られる。 （証終）
方程式 Ｘｎ≡ａ （ｍｏｄ ｐ） が
解を持つとき、 ａ を ｐ の ｎ 巾剰余
解を持たないとき、ａ を ｐ の ｎ 巾非剰余
という。 特に、ｎ＝２ のとき、平方剰余または平方非剰余といわれる。
（あっ！、やっと、これで前に述べた Ｌｅｇｅｎｄｒｅ の記号 と話がつながった！）
以上の話をまとめると、方程式 Ｘｎ≡ａ （ｍｏｄ ｐ） 、（ｎ ，ｐ−１）＝ｄ において、
ａ が ｐ で割り切れないとき、
ｄ＝１ ならば、 ａ は必ず、ｎ 巾剰余
ｄ＞１ ならば、 ｉｎｄｇ（ａ） が ｄ で割り切れる ａ は、ｎ 巾剰余で、その個数は、
（ｐ−１）/ｄ 個ある。
素数 ｐ と互いに素な自然数の個数は、オイラーの関数 φ（ｎ） で表されるが、上記の事実は、
φ（ｎ） 個のうち丁度 １/ｄ が、ｎ 巾剰余になる
ことを示している。特に、ｎ＝２ のときは、ｄ＝２ なので、丁度半分ということになる。
空舟さんからのコメントです。（平成２４年２月２９日付け）
素数ｐに対する原始根を求めるのは、私の認識では、適当な数ａをとって、ａ、ａ2、・・・を計
算してみて、もし原始根でなければ、そこに現れない他の数ｂで試して・・・という風にしらみつ
ぶしするしかないと認識しています。
砧 文夫 著『初等代数学』（1993）によると、原始根を具体的に求める一般的な方法はない
とのことで、ただ、1つさえ見つかれば、それを s として、ｐ-1 と素な数ｑに対して、sq も原始
根という風に残りは得られます。
空舟さんからのコメントです。（平成２４年２月２９日付け）
「適当な数ａをとって、ａ、ａ2、・・・を計算してみて・・・」と書きましたが、法997では、位数は
996の約数になるので、ａが、997の原始根であることを確かめるには、996=2・2・3・83
に注
意して、ａ498≠1、ａ332≠1、ａ12≠1 かどうかを調べれば十分。ａ249≠±1、ａ166≠±1、
ａ6≠±1でも良い。
具体的な計算としては、ａ6、ａ83を計算して、それらに±1があれば終了。(ａ83)2、(ａ83)3 も
計算して、それらも±1でなければ、ａは原始根。という風にすればだいぶ労力は減るでしょ
う。
せっかくなので、違う数 2・2・3・41+1＝493 の原始根を考えてみます。493は実は素数で
はないことが判明し、17・29 ということは、493は原始根を持たないので、考察終わり。
さて、話を、もとの Ｌｅｇｅｎｄｒｅ の記号 （ａ/ｐ） に戻そう。
有理素数 ｐ （ｐ≠２）と、ｐ で割り切れない整数 ａ において、上記の事実から、
|
|
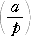＝（−１）ｉｎｄｇ（ａ） |
が成り立つ。
例 ｐ＝７ のとき、
|
| ａ |
１ |
２ |
３ |
４ |
５ |
６ |
| 指数 |
０ |
２ |
１ |
４ |
５ |
３ |
|
なので、
（１/７）＝１ 、（２/７）＝１ 、（３/７）＝−１ 、（４/７）＝１ 、（５/７）＝−１ 、（６/７）＝−１
より、 １ 、２ 、４ が平方剰余、 ３ 、５ 、７ が平方非剰余である。
または、上記の公式を用いないで、
１2≡１ （ｍｏｄ ７） 、 ３2≡２ （ｍｏｄ ７） 、 ５2≡４ （ｍｏｄ ７）
からも分かる。
Ｌｅｇｅｎｄｒｅ の記号 （ａ/ｐ） の性質
（１） ａ ≡ ｂ （ｍｏｄ ｐ） ならば、 （ａ/ｐ）≡（ｂ/ｐ）
（証明） ａ ≡ ｂ （ｍｏｄ ｐ） ⇔ ｉｎｄｇ（ａ） ≡ ｉｎｄｇ（ｂ） （ｍｏｄ ｐ−１） と
|
|
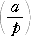＝ （−１）ｉｎｄｇ（ａ） |
の２つの事実から明らかであろう。 （証終）
（２） （ａｂｃ・・・/ｐ）＝（ａ/ｐ）（ｂ/ｐ）（ｃ/ｐ）・・・
（証明） ｉｎｄｇ（ａ×ｂ） ≡ ｉｎｄｇ（ａ） ＋ ｉｎｄｇ（ｂ） （ｍｏｄ ｐ−１） と
|
|
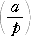＝ （−１）ｉｎｄｇ（ａ） |
の２つの事実から明らかであろう。 （証終）
定理（Ｅｕｌｅｒ の規準）
|
|
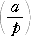≡ ａ(p-1)/2 （ｍｏｄ ｐ） |
（証明） 上記で示した定理Ｂにより、Ｘ2 ≡ ａ （ｍｏｄ ｐ） が解を持つための必要十分条
件は、 ａ(p - 1)/2 ≡ １ （ｍｏｄ ｐ） なので、
（ａ/ｐ）＝１ ならば、 ａ(p - 1)/2 ≡ １ （ｍｏｄ ｐ）
また、 （ａ/ｐ）＝−１ ならば、 ａp - 1 ≡ １ （ｍｏｄ ｐ） において、
ａ(p - 1)/2 −１ は、ｐ で割り切れないので、ａ(p - 1)/2 ＋１ が、ｐ で割り切れる。
すなわち、 （ａ/ｐ）＝−１ ならば、 ａ(p - 1)/2 ≡ −１ （ｍｏｄ ｐ）
以上から、定理が成り立つ。 （証終）
例 前述の例で、
（１/７）＝１ 、（２/７）＝１ 、（３/７）＝−１ 、（４/７）＝１ 、（５/７）＝−１ 、（６/７）＝−１
であることを、指数表を活用して求めたが、上記の定理によれば、次のようにしても求める
ことが出来る。
１3 ≡ １ （ｍｏｄ ７）、 ２3 ≡ １ （ｍｏｄ ７）、 ３3 ≡ −１ （ｍｏｄ ７）
４3 ≡ １ （ｍｏｄ ７）、 ５3 ≡ −１ （ｍｏｄ ７）、 ６3 ≡ −１ （ｍｏｄ ７）
（コメント） ７ で割った余りは、０、１、２、３、４、５、６ で、その平方を７で割った余りは、そ
れぞれ ０、１、４、２、２、４、１ となるので、０、１、２、４
の場合のみが平方剰余
となる。指数というものを用いて、（ａ/ｐ）を考えてきたが、何やら遠回りをしている
ような．．．？多分もっと素晴らしい応用があるのだろう。それを信じて先に進もう！
さて、当面の問題：
有理素数 ｐ が、４で割って１余る数のとき、方程式 ｘ2＋ｙ2 ＝ ｐ は、どのような解を持つ
のか？
に、ここで話を戻そう。
例 ４で割って１余る有理素数 ｐ としては、ｐ＝５、１３、１７、２９、３７、４１、５３、・・・
これらに対しては、
５＝１2＋２2 、１３＝２2＋３2 、１７＝１2＋４2 、２９＝２2＋５2 、３７＝１2＋６2
４１＝４2＋５2 、５３＝２2＋７2 、・・・
などと表され、取りあえずは解をもつことが予想される。
実は、次の定理が成り立つ。
定理（フェルマー・オイラーの素数定理）
有理素数 ｐ が、４で割って１余る数のとき、方程式 ｘ2＋ｙ2 ＝ ｐ は、有理整数解
を必ず持つ。
（この事実を初めて発見したのはフェルマー（１６６０年）だが、証明はオイラーが初めて（？）
与えたらしい。）
この定理から、４で割って１余る有理素数は、ガウスの整数としては、合成数となる。
（証明） Ｅｕｌｅｒ の規準から、 （−１/ｐ）＝ （−１）(p-1)/2
ここで、ｐ は４で割って１余る数なので、 （ｐ−１）/２ は偶数。
よって、 （−１/ｐ）＝１ となり、 −１ は ｐ の平方剰余となる。
したがって、 方程式 Ｘ2≡−１ （ｍｏｄ ｐ） は有理整数解を持つ。
このとき、 Ｘ2＋１＝( Ｘ＋ ｉ )( Ｘ− ｉ ) は、ｐ で割り切れる。（ ｉ は、虚数単位）
ここで、 Ｘ− ｉ と ｐ の最大公約数を ε とおくと、ε は、ｐ の約数なので、
ε ＝ １ または ε ＝ ｐ または ε ＝ ｚ （ただし、ｐ＝ｚ・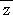 ） の何れかが成り立つ。
ε ＝ １ のとき、
Ｘ＋ ｉ 、 Ｘ− ｉ ともに ｐ と互いに素、すなわち、Ｘ2＋１ は ｐ と互いに素
これは、Ｘ2＋１ が、ｐ で割り切れることに矛盾。
ε ＝ ｐ のとき、Ｘ− ｉ が ｐ で割り切れることになり、矛盾。
したがって、 ε ＝ ｚ ＝ ａ＋ｂ・ｉ で、このとき、ｐ＝ｚ・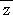 でなければならない。
ここで、ｐ≠０ なので、 ａ≠±ｂ より、 ｚ と 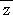は互いに同伴数にはなり得ない。
以上から、
４で割って１余る有理素数は、ガウスの整数として、２つの異なる互いに共役な素数の積
として表される。 （証終）
上記証明で用いられた事実をさらに深めて、整数論の基本定理（平方剰余の相互法則）
が得られる。
定理
（１） 平方剰余の相互法則
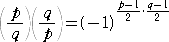
（２） 第一補充法則
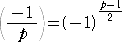
（３） 第二補充法則
この相互法則の最初の完全なる証明は、Ｇａｕｓｓ によるといわれる。
以下、工事中！