
日常生活で次のような計算をする可能性は全くないが、その爽快さは、例えば、苦しみ
抜いていた懸案の難題がある瞬間に雲散霧消したかのように解決するときに似ている。
こちらの方は誰でもが経験しうることだろう。 (→ 参考:「部分分数分解の真実」)
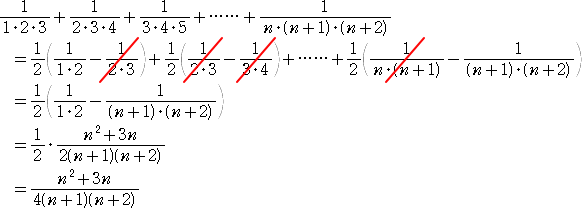
また、次のようなものも数学ではよく見かける計算である。
1・2・3+2・3・4+3・4・5+・・・・・・+n・(n+1)・(n+2)
解き方を見る限りにおいて、両者は全く別な解法の問題と考えられる。
ところが、別な視点で両者を見つめると、実は全く同じ範疇の問題であることが頷ける。
こんなことを
淡中忠郎 著 数学の学校 (東京書籍)
(もう絶版かもしれない! 私は図書館から無償で手に入れることが出来たが...ラッキーかな?)
から学ぶことができた。
このことを、このページでまとめてみようと思う。
関数 F(x) に対して、 ΔF(x)=F(x+1)−F(x) とおく。
このとき、 Δ2F(x)=Δ(ΔF(x)) と考えれば、
Δ2F(x)=ΔF(x+1)−ΔF(x)
=F(x+2)−F(x+1)−{F(x+1)−F(x)}
=F(x+2)−2F(x+1)+F(x)
同様にして、
Δ3F(x)=Δ2F(x+1)−Δ2F(x)
=F(x+3)−2F(x+2)+F(x+1)−{F(x+2)−2F(x+1)+F(x)}
=F(x+3)−3F(x+2)+3F(x+1)−F(x)
Δ4F(x)=Δ3F(x+1)−Δ3F(x)
=F(x+4)−3F(x+3)+3F(x+2)−F(x+1)
−{F(x+3)−3F(x+2)+3F(x+1)−F(x)}
=F(x+4)−4F(x+3)+6F(x+2)−4F(x+1)+F(x)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
このような計算をしていると、あたかも (x−1)n の形の展開をしているような錯覚に陥る。
そこで、この怪しげな感覚を正当化するために、
変換 X : F(x) → F(x+1)
を考えると、上記の計算は、
ΔF(x)=F(x+1)−F(x)=XF(x)−F(x)=(X−1)F(x)
と考えられ、さらに、
Δ2F(x)=Δ(X−1)F(x)=(X−1)2F(x)
Δ3F(x)=Δ2(X−1)F(x)=Δ(X−1)2F(x)=(X−1)3F(x)
Δ4F(x)=Δ3(X−1)F(x)=Δ2(X−1)2F(x)=Δ(X−1)3F(x)=(X−1)4F(x)
となる。
ここで、 XF(x)=F(x+1) から、 X2F(x)=XF(x+1)=F(x+2)
同様にして、 X3F(x)=X2F(x+1)=XF(x+2)=F(x+3)
X4F(x)=X3F(x+1)=X2F(x+2)=XF(x+3)=F(x+4)
なので、
Δ4F(x)=(X−1)4F(x)
=(X4−4X3+6X2−4X+1)F(x)
=X4F(x)−4X3F(x)+6X2F(x)−4XF(x)+F(x)
=F(x+4)−4F(x+3)+6F(x+2)−4F(x+1)+F(x)
となる。このことから、(x−1)n の形の展開をしているような気分になるのは必然であった
わけである。
いま、 (x)n=x・(x−1)・(x−2)・・・・・(x−n+1) と置くことにする。
すなわち、 (x)=x 、 (x)2=x(x−1) 、 (x)3=x(x−1)(x−2) 、 ・・・ である。
このとき、 Δ(x)=(x+1)−x=1
Δ(x)2=(x+1)x−x(x−1)=2x=2(x)
Δ(x)3=(x+1)x(x−1)−x(x−1)(x−2)=3x(x−1)=3(x)2
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
このような計算を見ていると、 微分の公式
(x)’=1 、 (x2)’=2x 、 (x3)’=3x2 、 ・・・・・・・・・
に似ていることが頷ける。
同様に、
と置くことにすると、
Δ(x)-1=1/(x+1)−1/x=−1/{x(x+1)}=−(x)-2
Δ(x)-2=1/{(x+1)(x+2)}−1/{x(x+1)}=−2/{x(x+1)(x+2)}=−2(x)-3
Δ(x)-3=1/{(x+1)(x+2)(x+3)}−1/{x(x+1)(x+2)}
=−3/{x(x+1)(x+2)(x+3)}=−3(x)-4
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
このような計算を見ていると、やはり 微分の公式
(x-1)’=−x-2 、 (x-2)’=−2x-3 、 (x-3)’=−3x-4 、 ・・・・・・・・・
に似ていることが了解される。
ここで、 (x)0=1 と約束すると、 Δ(x)0=1−1=0 が成り立つ。
以上から、適切に (x)n を定義すると、
Δ(x)n=n(x)n-1 ( n は整数 )
という微分の公式によく似た性質を「Δ」は持っていることが伺える。
ここで、 ΔG(x)=G(x+1)−G(x) であったことを思い出すと、関数 F(x) に対して、
ΔG(x)=F(x)
となる関数 G(x) が存在すれば、
G(x+1)−G(x)=F(x)
である。(← これは、階差そのものですね!)
このとき、
が成り立つ。したがって、2つの数 a 、b (a≦b)に対して、
となる。 そこで、
とおくと、
が成り立つ。(← これは、定積分に似ていますね!)
この公式を、冒頭の問題に適用してみよう。
まず、 1・2・3+2・3・4+3・4・5+・・・・・・+n・(n+1)・(n+2) については、
F(x)=(x)3 として、 Δ(x)4=4(x)3 から、 G(x)=(x)4/4 なので、
1・2・3+2・3・4+3・4・5+・・・・・・+n・(n+1)・(n+2)
=F(3)+F(4)+・・・+F(n+2)
=[(x)4/4]n+33
={n(n+1)(n+2)(n+3)−3・2・1・0}/4
=n(n+1)(n+2)(n+3)/4
となり、先の結果と一致する。
また、
については、
F(x)=(x)-3 として、 Δ(x)-2=−2(x)-3 から、 G(x)=−(x)-2/2 なので、
与式=F(1)+F(2)+・・・+F(n)
=[−(x)-2/2]n+11
={−1/{(n+1)(n+2)}+1/2}/2
=(n2+3n)/4{(n+1)(n+2)}
となり、先の結果と一致する。
(コメント) 冒頭では異なる解法だったのに、視点を変えて見ると、ホントに同じ解法の問題
になってしまいました!驚きです...。