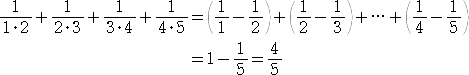部分分数分解の真実 
よくクイズで、
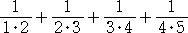
の値を求めよ!という風な問題が出されるときがある。4項だけなので、強引に計算しても
求まるが、「5秒で答えよ。」なんて言われたら焦ってしまう。この問題を見て、
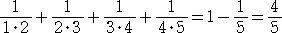
と即答できる人は相当クイズ慣れしている方だろう。次の式変形 :
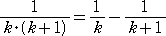
がこの問題を攻略するポイントで、部分分数分解と言われる手法である。すなわち、
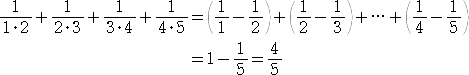
と求められる。
この部分分数分解の手法は、いろいろな数列の和や積分計算で活躍するが、知ってい
て損はしないテクニックである。(→参考:連立方程式の回避)私が高校生の頃は高校1年
次に教わったが、つい最近までは高校3年次、平成15年から施行された新学習指導要領
においては、高校2年次で学ぶことになっている。
部分分数分解というと上記のような式変形に終始し、その幾何学的意味というものを今ま
で深く考えることはなかった。最近その幾何学的意味を知る機会があり、このページに整理
しておこうと思う。
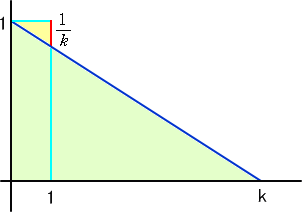 |
左図において、
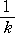
が意味づけられる。 |
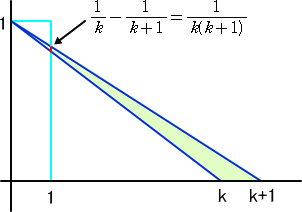 |
このことを利用すると、
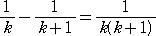
となり、
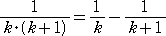
の幾何学的意味が明らかとなる。 |
したがって、
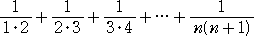
の和を求めるには、

上図から、

とすればよいことが分かる。
(追記) 令和6年11月24日付け
次の東北大学 文系(1986)の問題は、部分分数分解の問題である。
問題 数列{an}を a1=3、ak+1=4ak+3 (k=1、2・・・) で帰納的に定義する。
(1) 一般項 an を求めよ。
(2) 次の和 Σk=1n 1/(log2(ak+1)log2(ak+1+1)) を求めよ。
(解)(1) ak+1+1=4(ak+1) から、 an+1=4n なので、an=4n−1
(2) (1)より、
Σk=1n 1/(log2(ak+1)log2(ak+1+1))=Σk=1n 1/(2k(2k+2))
=(1/4)Σk=1n (1/k−1/(k+1))=(1/4)(1−1/(n+1))=n/(4(n+1)) (終)
kuiperbelt さんからのコメントです。(令和6年11月26日付け)
1/(k*(k+1)*(k+2))=(1/2)*(1/(k*(k+1))-1/((k+1)*(k+2)))
1/(k*(k+1)*(k+2)*(k+3))=(1/3)*(1/(k*(k+1)*(k+2))-1/((k+1)*(k+2)*(k+3)))
・・・・・
1/(k*(k+1)*(k+2)*...*(k+m))=(1/m)*(1/(k*(k+1)*...*(k+m-1))-1/((k+1)*(k+2)*...*(k+m)))
なので、
1/(1*2*3)+1/(2*3*4)+...+1/(n*(n+1)*(n+2))=(1/2)*(1/(1*2)-1/((n+1)*(n+2)))
1/(1*2*3*4)+1/(2*3*4*5)+...+1/(n*(n+1)*(n+2)*(n+3))=(1/3)*(1/(1*2*3)-1/((n+1)*(n+2)*(n+3)))
・・・・・
1/(1*2*3*...*(m+1))+...+1/(n*(n+1)*(n+2)*...*(n+m))=(1/m)*(1/m!-n!/(n+m)!)
というのも言えますね。
(追記) 令和6年12月27日付け
次の東北大学 理系(1988)の問題も、部分分数分解の問題である。
問題5 数列{an}は任意の自然数nに対して、Σk=0n-1 3-kan-k=1/{n(n+1)(n+2)}
を満たしているとする。このとき、m≧3に対して、Σn=1m nan を求めよ.
(解) an+(1/3)an-1+(1/32)an-2+・・・+(1/3n-1)a1=1/{n(n+1)(n+2)}
n≧2 のとき、an-1+(1/3)an-2+(1/32)an-3+・・・+(1/3n-2)a1=1/{n(n−1)(n+1)}
よって、n≧2 のとき、
an=1/{n(n+1)(n+2)}−1/{3n(n−1)(n+1)} で、 a1=1/6
このとき、
nan=1/{(n+1)(n+2)}−1/{3(n−1)(n+1)}
=1/(n+1)−1/(n+2)−(1/6){1/(n−1)−1/(n+1)} なので、
Σn=1m nan=1/6+Σn=2m nan
=1/6+{1/3−1/(m+2)}−(1/6){1+1/2−1/m−1/(m+1)}
=1/4−(4m2+m−2)/{6m(m+1)(m+2)}
=(3m3+m2+4m+4)/{12m(m+1)(m+2)} (終)
(追記) 令和7年3月19日付け
次の東北大学 後期理系(1990)の問題も、部分分数分解の問題である。
問題 n=0、1、2、・・・ に対し、Hn={(a,b,c)|a,b,c は負でない整数で、a+b+c=n}
とおき、Hnの要素の個数をhnとおく。和 Σn=0∞ (1/hn) を求めよ。
(解) 題意より、hn=3Hn=n+2Cn=(n+2)(n+1)/2 なので、
1/hn=2/{(n+2)(n+1)}=2(1/(n+1)−1/(n+2))
よって、第n部分和 Σk=0n (1/hk)=2(1−1/(n+2)) より、
Σn=0∞ (1/hn)=2 (終)
(追記) 令和7年5月5日付け
次の東北大学 後期文系(1992)の問題も、部分分数分解の問題である。
問題 次の和を求めよ。
Σk=1n k/(12+32+52+・・・+(2k−1)2)
(解) 12+32+52+・・・+(2n−1)2
=Σk=1n (2k−1)2=Σk=1n (4k2−4k+1)=n(2n−1)(2n+1)/3 より、
与式=Σk=1n 3/{(2k−1)(2k+1)}
=(3/2){Σk=1n 1/(2k−1)−1/(2k+1)}=3n/(2n+1) (終)
(追記) 令和7年5月9日付け
次の東北大学 前期理系(1993)の問題も、部分分数分解の問題である。
問題 r、nを自然数、kを 0≦k≦n を満たす整数とする。1、2、・・・、r+n から r+k 個
の数を取り出すとき、その中に 1、2、・・・、r がすべて含まれる確率を an とおく。
(1) an を r、n、k の式として表せ。
(2) r≧2 のとき、Σn=1∞ an を求めよ。
(解)(1) an=nCk/r+nCr+k=n!(r+k)!/(k!(r+n)!)
(2) an=(r+k)!/k!・1/{(r+n)(r+n−1)・・・(n+1)}
=(r+k)!/{k!(r−1)}・(1/{(r+n−1)・・・(n+1)}−1/{(r+n)・・・(n+2)})
なので、
Σn=1m an=(r+k)!/{k!(r−1)}・(1/r!−1/{(r+m)・・・(m+2)})
より、 Σn=1∞ an =(r+k)!/{k!r!(r−1)} (終)
(追記) 令和7年6月16日付け
次の東北大学 前期理系(1995)の問題も、部分分数分解の考え方を用いる問題である。
問題 0<u<π/4、0<θ<π/2 とする。
(1) 1/tanu−2/tan2u を簡単にせよ。
(2) 無限級数 Σn=1∞ (1/2n)tan(θ/2n) の和を求めよ。
ただし、limx→0 (1/x)tanx =1 を用いてよい。
(解)(1) 1/tanu−2/tan2u=cosu/sinu−cos2u/(sinucosu)
=(cos2u−cos2u+sin2u)/(sinucosu)=sinu/cosu=tanu
(2) (1)より、 k=1、2、・・・、n について、
(1/2k)tan(θ/2k)=(1/2k)(1/tan(θ/2k)−2/tan(θ/2k-1))
=(1/2k)(1/tan(θ/2k))−(1/2k-1)(1/tan(θ/2k-1))
なので、 Σk=1n (1/2k)tan(θ/2k)=(1/2n)(1/tan(θ/2n))−1/tanθ
ここで、limx→0 (1/x)tanx =1 より、
(1/2n)(1/tan(θ/2n))=1/(θ・tan(θ/2n)/(θ/2n))→1/θ なので、
Σn=1∞ (1/2n)tan(θ/2n)=1/θ−1/tanθ (終)
(追記) 令和7年8月31日付け
次の東北大学 後期理系(1998)の問題も、部分分数分解の考え方を用いる問題である。
問題 {1/an}は、初項1/a、公差dの等差数列とする。このとき、
limn→∞ (a1a2+a2a3+・・・+anan+1) を求めよ.
(解) 題意より、 1/an=1/a+(n−1)d=(1+(n−1)ad)/a なので、
an=a/(1+(n−1)ad)
よって、d≠0 のとき、
a1a2+a2a3+・・・+anan+1
=a2/(1+ad)+a2/{(1+ad)(1+2ad)}+・・・+a2/{(1+(n−1)ad)(1+nad)}
=a2/(1+ad)+(a/d)(1/(1+ad)−1/(1+2ad))+・・・+(a/d)(1/(1+(n−1)ad)−1/(1+nad))
=a2/(1+ad)+(a/d)(1/(1+ad)−1/(1+nad))
→ a2/(1+ad)+(a/d)/(1+ad)=a/d (ただし、n → ∞)
d=0 のとき、 a1a2+a2a3+・・・+anan+1=na2 → ∞ (ただし、n → ∞) (終)
以下、工事中!