らすかるさんのＨＰに「三角関数表」が掲載されていた。その表を眺めていたら、次の値に
ついては手計算で求めてみようという雰囲気にさせてくれる。他の値は見通しをつけるのが
難しそう．．．。
０°、３０°、４５°、６０°、９０°の５つについては、自明としていいだろう。
１５°、７５°については、加法定理の活用例として適切だろう。
ただ、次のような図形的解法も存在する。
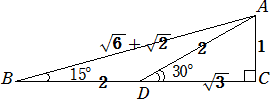
図より、 ｓｉｎ１５°＝１/（
＋
）＝（−）/４＝ｃｏｓ７５°ｃｏｓ１５°＝（２＋
）/（＋）＝（＋）/４＝ｓｉｎ７５°ｔａｎ１５°＝１/（２＋
）＝２−１８°、２２．５°、３６°、５４°、６７．５°、７２°についても図形を利用して求めることが
出来る。
○ ２２．５°、６７．５°の場合
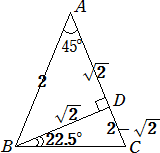
図より、 ｔａｎ２２．５°＝（２−
）/＝−１ここで、 ＢＣ＝２√（２−
） なので、ｓｉｎ２２．５°＝（２−
）/｛２√（２−）｝＝√（２−）/２＝ｃｏｓ６７．５°ｃｏｓ２２．５°＝
/｛２√（２−）｝＝√（２＋）/２＝ｓｉｎ６７．５°○ １８°、３６°、５４°、７２°の場合（→ 参考：「正５角形の作図と折り紙」）
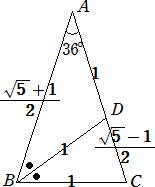
図より、 ｓｉｎ１８°＝（
−１）/４＝ｃｏｓ７２°ここで、 １−（
−１）2/１６＝（１０＋２）/１６ より、ｃｏｓ１８°＝√（１０＋２
）/４＝ｓｉｎ７２°ｔａｎ１８°＝｛（
−１）/４｝/｛√（１０＋２）/４｝＝√（２５−１０）/５同様にして、 ｃｏｓ３６°＝（
＋１）/４＝ｓｉｎ５４°ここで、 １−（
＋１）2/１６＝（１０−２）/１６ より、ｓｉｎ３６°＝√（１０−２
）/４＝ｃｏｓ５４°ｔａｎ３６°＝｛√（１０−２
）/４｝/｛（＋１）/４｝＝√（５−２）あと、図形で求められる角度は、いくつ．．．。
（追記） 令和７年１０月１１日付け
次の東北大学 後期文系（２０００）の問題は、ｓｉｎ１５°、ｃｏｓ１５°、ｔａｎ１５°の計算に
新しい視点を与えてくれる。
問題 ∠ＡＢＣ＝∠ＡＣＢ＝１５° である三角形ＡＢＣについて、線分ＡＢを点Ａの側へ延
長して、その上に点Ｄをとり、ＡＤ＝ＢＣ となるようにする。このとき、次の問いに答えよ。
（１） ｓｉｎ１５°、ｃｏｓ１５°、ｔａｎ１５° を求めよ。
（２） ∠ＡＤＣ＝θ とおくとき、ｓｉｎθの値を求めよ。
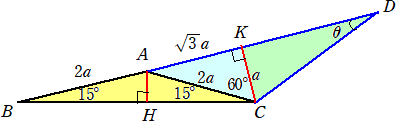
（解）（１） 上図において、 ＢＣ2＝ａ2＋（２＋
）2ａ2＝（８＋４）ａ2 より、ＢＣ＝（
＋）ａ となる。よって、 ｓｉｎ１５°＝１/（
＋）＝（−）/４ｃｏｓ１５°＝（
＋２）/（＋）＝（＋）/４ｔａｎ１５°＝１/（
＋２）＝２−（２） 上図において、 ＡＤ＝ＢＣ＝４ａｃｏｓ１５°＝（
＋）ａこのとき、 ＫＤ＝（
−＋）ａ なので、ＣＤ2＝（
−＋）2ａ2＋ａ2＝（１２−６＋４−２）ａ2よって、 ｓｉｎθ＝１/√｛１２−６
＋４−２｝ （終）（コメント） 問題文のヒントが秀逸ですね。そのヒントがなければ、通常次のように解くだろう
と思います。
（１） ＡＢ＝ＡＣ＝１ としても一般性を失わない。Ａより底辺ＢＣに垂線を下ろし、その足
をＨとおく。このとき、ＡＨ＝ｓｉｎ１５°、ＢＣ＝２ｃｏｓ１５° である。
余弦定理より、 ４ｃｏｓ2１５°＝１＋１−２ｃｏｓ１５０°＝２＋
よって、 ２ｃｏｓ１５°＝（
＋１）/＝（＋）/２ から、 ｃｏｓ１５°＝（＋）/４また、 （１/２）・（
＋）/２・ｓｉｎ１５°＝（１/２）ｓｉｎ１５０°＝１/４ から、ｓｉｎ１５°＝１/（
＋）＝（−）/４このとき、 ｔａｎ１５°＝（
−）/（＋）＝（８−４）/４＝２−（追記） 令和７年１１月１日付け
次の東北大学 後期文系（２００１）の問題は、文字の消去に気が付けば容易だろう。
問題 ａ は定数で、−９０°＜ｔ＜９０°とする。２点
Ｐ（（１/２）ｓｉｎｔ＋ｃｏｓ２ｔ，ｔａｎｔ） 、Ｑ（ｓｉｎ２ｔ＋ａｃｏｓｔ，３ｓｉｎｔ−２ｃｏｓｔ＋ａ＋２）
がある ｔ に対して同じ点となるとき、定数 ａ の値およびそのときの ｔ の値を求めよ。
（解） （１/２）ｓｉｎｔ＋ｃｏｓ２ｔ＝ｓｉｎ２ｔ＋ａｃｏｓｔ
ｔａｎｔ＝３ｓｉｎｔ−２ｃｏｓｔ＋ａ＋２ がある ｔ に対して成り立つ。
ａ＝ｔａｎｔ−３ｓｉｎｔ＋２ｃｏｓｔ−２ を第１式に代入して、
（１/２）ｓｉｎｔ＋ｃｏｓ２ｔ＝ｓｉｎ２ｔ＋（ｔａｎｔ−３ｓｉｎｔ＋２ｃｏｓｔ−２）ｃｏｓｔ
から、 （１/２）ｓｉｎｔ＋ｃｏｓ2ｔ−ｓｉｎ2ｔ＝２ｓｉｎｔｃｏｓｔ＋ｓｉｎｔ−３ｓｉｎｔｃｏｓｔ＋２ｃｏｓ2ｔ−２ｃｏｓｔ
すなわち、 ｓｉｎｔｃｏｓｔ−（１/２）ｓｉｎｔ＋２ｃｏｓｔ−１＝０
よって、 （ｃｏｓｔ−１/２）（ｓｉｎｔ＋２）＝０ より、 ｓｉｎｔ＋２≠０ から、 ｃｏｓｔ＝１/２
−９０°＜ｔ＜９０°より、 ｔ＝±６０°
ｔ＝６０° のとき、
ａ＝ｔａｎｔ−３ｓｉｎｔ＋２ｃｏｓｔ−２＝
−（３/２）−１＝−１−（１/２）ｔ＝−６０° のとき、
ａ＝ｔａｎｔ−３ｓｉｎｔ＋２ｃｏｓｔ−２＝−
＋（３/２）−１＝−１＋（１/２） （終）（追記） 令和７年１１月１９日付け
次の東北大学 後期文系（２００２）の問題は、測量問題である。
問題 水平な地面に垂直に塔が建っている。目の高さ１．５ｍの人が地面のある地点Ａに
立って塔の頂上を見上げると、仰角がθであった。ただし、θ＞０°とする。この人が塔に
向かって１６０ｍ近づいて見上げると、仰角が２θになった。さらに１００ｍ近づいて見上げ
ると、仰角が４θになった。以下の問いに答えよ。
（１） ｃｏｓθの値を求めよ。
（２） 塔の高さを求めよ。
（３） 同じ人が地点Ａから塔に向かって何ｍ近づくと、塔の頂上を見上げる仰角が３θになるか。
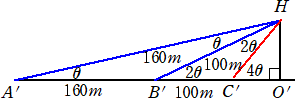
（解）（１） △ＨＢ’Ｃ’において、余弦定理より、
１００2＝１００2＋１６０2−２・１００・１６０ｃｏｓ２θ
すなわち、 ２・１００・ｃｏｓ２θ＝１６０ より、 ｃｏｓ２θ＝４/５
２ｃｏｓ2θ−１＝４/５ より、 ｃｏｓθ＝３/
（２） ＯＨ’＝１００ｓｉｎ４θ＝２００ｓｉｎ２θｃｏｓ２θ
ここで、ｃｏｓ２θ＝４/５ より、 ｓｉｎ２θ＝３/５ なので、
ＯＨ’＝２００（３/５）（４/５）＝９６
よって、塔の高さは、 ＯＨ’＋１．５＝９７．５（ｍ）
（３） 塔の頂上を見上げる仰角が３θになる地点をＤとし、目線の位置をＤ’とする。
∠Ｂ’ＨＤ’＝θ より、∠Ｄ’ＨＣ’＝θ なので、 線分ＨＤ’は∠Ｂ’ＨＣ’の２等分線となる。
よって、 Ｂ’Ｄ’ ： Ｄ’Ｃ’＝１６０ ： １００＝８ ： ５ となる。
このことから、 Ｂ’Ｄ’＝１００×（８/１３）＝８００/１３ となるので、
地点Ａから塔に向かって、 １６０＋８００/１３＝２８８０/１３（ｍ） 近づけばよい。 （終）
以下、工事中！