
丂尰峴偺妛廗巜摫梫椞偱偼丄崅峑侾擭偱嶰妏斾偺掕媊偍傛傃偦偺恾宍傊偺墳梡傪妛傃丄
崅峑俀擭偱偼娭悢偲偟偰堖懼偊偟丄嶰妏娭悢偍傛傃偦偺僌儔僼傪妛傇丅
丂嫵壢彂偱偼丄婎杮偺僌儔僼偐傜偦傟傜偺娭學傪攃埇偡傞偺偵偲偳傑偭偰偄傞丅
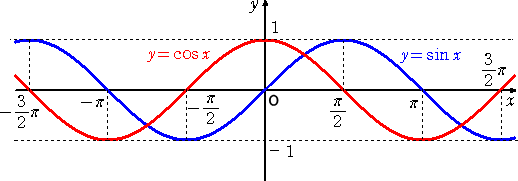
丂崅峑俁擭偱嶰妏娭悢偺旝暘傪妛廗偟偰丄嶰妏娭悢偲弶摍娭悢偲偺娭學傪抦傞偙偲偵側傞丅
偦偺拞偱戝愗側娭學偼丄師偺晄摍幃偩傠偆丅
丂丂倶 亞 侽丂偺偲偒丄丂倶 亞 倱倝値 倶 丂丂丂偨偩偟丄摍崋惉棫偼丄倶亖侽丂偺偲偒偵尷傞
偙偺晄摍幃偺徹柧偼堈偟偄丅
乮徹柧乯丂俥乮倶乯亖 倶 亅 倱倝値 倶丂偲偍偔偲丄丂俥乫乮倶乯亖 侾 亅 們倧倱 倶 亞侽丂傛傝丄
丂俥乮倶乯偼扨挷憹壛娭悢偲側傞丅
傑偨丄俥乮侽乯亖侽丂側偺偱丄丂倶 亞 侽丂偺偲偒丄丂俥乮倶乯 亞侽丂偲側傞丅
丂傛偭偰丄 倶 亞 侽丂偺偲偒丄丂丂倶 亞 倱倝値 倶丂偑惉傝棫偮丅丂乮徹廔乯
丂偙偺晄摍幃偼丄捈慄 倷亖倶 偑丄嬋慄 倷亖倱倝値 倶 偺尨揰偵偍偗傞愙慄偱偁傞偲偄偆娭學偐傜
傕捈姶揑偵庴偗擖傟傗偡偄丅
丂暯惉侾俈擭係寧俀俋擔丄摉俫俹偺宖帵斅乽弌夛偄偺愹乿偵俫俶乽億儖僥乿偝傫偲偄偆曽偐傜幙栤
偑婑偣傜傟偨丅
丂丂倱倝値(們倧倱 倶) 偲丂們倧倱(倱倝値 倶)丂偵偮偄偰丄丂們倧倱(倱倝値 倶)亜倱倝値(們倧倱 倶)丂偑惉傝棫偮偙偲偼丄
僌儔僼昤夋僜僼僩傪梡偄偰暘偐傞偑丄寁嶼偱偼丄偳偆帵偣偽偄偄偺偩傠偆偐丠
丂幚嵺偵丄僌儔僼昤夋僜僼僩傪梡偄偰俀偮偺嬋慄偺奣宍傪昤偐偣偰傒偨丅
丂

丂僌儔僼偐傜丄妋偐偵晄摍幃偺惉傝棫偮偙偲偑椆夝偝傟傞丅
偝傜偵丄忋恾偐傜丄丂倷亖倱倝値(們倧倱 倶)丂偼丄廃婜 俀兾丂偺廃婜娭悢
丂倷亖們倧倱(倱倝値 倶)丂偼丄廃婜 兾丂偺廃婜娭悢
偱偁傞偙偲偑梊憐偝傟傞丅幚嵺偵丄
丂倱倝値(們倧倱 乮俀兾亄倶)乯亖倱倝値(們倧倱 倶)丂丄丂們倧倱(倱倝値 乮兾亄倶)乯亖們倧倱(亅倱倝値 倶)亖們倧倱(倱倝値 倶)
偐傜柧傜偐偱偁傠偆丅
丂乽億儖僥乿偝傫偺栤戣偵懳偟偰丄摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽傜偡偐傞乿偝傫偑丄
晄摍幃丂乽丂倶 亞 侽丂偺偲偒丄丂倶 亞 倱倝値 倶丂乿傪妶梡偟偰丄柧夝偵夝寛偝傟偨丅
丂埲壓偼丄傜偡偐傞偝傫偺夝摎偵庒姳偺曗懌傪偟偰傑偲傔偨傕偺偱偁傞丅
傑偢
丂俀偮偺嬋慄 倷亖倱倝値(們倧倱 倶) 偲 倷亖們倧倱(倱倝値 倶)丂偼丄捈慄 倶亖 兾 偵娭偟偰慄懳徧
偱偁傞偙偲傪帵偡丅
幚嵺偵丄 倱倝値(們倧倱 乮兾亄倶))亖倱倝値(亅們倧倱 倶)亖亅倱倝値(們倧倱 倶)
丂倱倝値(們倧倱 乮兾亅倶))亖倱倝値(亅們倧倱 倶)亖亅倱倝値(們倧倱 倶)
傛偭偰丄丂倱倝値(們倧倱 乮兾亄倶))亖倱倝値(們倧倱 乮兾亅倶))丂傛傝丄惉傝棫偮丅
摨條偵丄 們倧倱(倱倝値 乮兾亄倶))亖們倧倱(亅倱倝値 倶)亖們倧倱(倱倝値 倶)
丂們倧倱(倱倝値 乮兾亅倶))亖們倧倱(倱倝値 倶)
傛偭偰丄丂們倧倱(倱倝値 乮兾亄倶))亖們倧倱(倱倝値 乮兾亅倶))丂傛傝丄惉傝棫偮丅
傑偨丄丂倷亖倱倝値(們倧倱 倶)丂丄倷亖們倧倱(倱倝値 倶)丂偼丄偦傟偧傟廃婜 俀兾丄兾丂偺廃婜娭悢側偺偱丄
峫偊傞 倶 偺斖埻偲偟偰丄丂侽 亝 倶 亝 兾丂偲偟偰傕堦斒惈傪幐傢側偄丅
傑偢丄丂侽 亝 倶 亙 兾/俀丂偺偲偒丄丂倷亖們倧倱 倶 偼扨挷尭彮偱丄丂倶 亞 倱倝値 倶丂傛傝丄
丂們倧倱 倶 亝 們倧倱乮倱倝値 倶乯丂偡側傢偪丄丂們倧倱乮倱倝値 倶乯亞 們倧倱 倶
丂傑偨丄丂們倧倱 倶 亜 侽丂側偺偱丄丂們倧倱 倶 亜 倱倝値 乮們倧倱 倶乯
忋婰偺俀偮偺晄摍幃傛傝丄丂們倧倱乮倱倝値 倶乯亜 倱倝値 乮們倧倱 倶乯丂丂偑惉傝棫偮丅
師偵丄丂兾/俀 亝 倶 亝 兾丂偺偲偒丄丂亅兾/俀 亙 們倧倱 倶 亝 侽丂側偺偱丄倱倝値 乮們倧倱 倶乯 亝 侽
堦曽丄丂侽 亝 倱倝値 倶 亙 兾/俀丂側偺偱丄丂們倧倱乮倱倝値 倶乯亜 侽丂偑惉傝棫偮丅
忋婰偺俀偮偺晄摍幃傛傝丄丂們倧倱乮倱倝値 倶乯亜 倱倝値 乮們倧倱 倶乯丂丂偑惉傝棫偮丅
丂埲忋偐傜丄侽 亝 倶 亝 兾丂偺偲偒丄丂們倧倱乮倱倝値 倶乯亜 倱倝値 乮們倧倱 倶乯丂偑惉傝棫偪丄廬偭偰丄
丂慡偰偺幚悢 倶 偵懳偟偰丄丂們倧倱乮倱倝値 倶乯亜 倱倝値 乮們倧倱 倶乯
偑惉傝棫偮丅
乮僐儊儞僩乯丂崱傑偱偁傑傝婥偵偲傔側偐偭偨晄摍幃乽丂倶 亞 侽丂偺偲偒丄丂倶 亞 倱倝値 倶丂乿偺椡嫮
丂丂丂丂丂偄僷儚乕偵巚傢偢傂傟暁偟傑偟偨両偙偺傛偆側婡夛傪梌偊偰偄偨偩偄偨傜偡偐傞偝傫
丂丂丂丂丂偲幙栤幰偺億儖僥偝傫偵姶幱偄偨偟傑偡丅
乮捛婰乯丂暯惉侾俉擭俁寧侾擔丄摉俫俹偺宖帵斅乽弌夛偄偺愹乿偵丄俫俶乽傐傞偰乿偝傫偐傜媣乆偺
丂丂丂彂偒崬傒偑偁偭偨丅庴尡傕廔傢偭偰偁偲偼崌奿敪昞傪懸偮乧両偩偗偲偄偆帪娫偺拞偱丄
丂丂丂忋婰偺暿夝(丠)偵宷偑傝偦偆側傕偺傪敪尒偝傟偨偲偺偙偲偱偁傞丅
丂偙偙偱偼丄傐傞偰偝傫偺敪尒偝傟偨暿夝傪徯夘偟偨偄偲巚偆丅
亅兾/俀 亙 倳 亙 兾/俀丂丄亅兾/俀 亙 倴 亙 兾/俀丂偺偲偒丄丂倱倝値 倳 亙 們倧倱 倴丂傪枮偨偡揰
乮 倳 丆 倴 乯 偺懚嵼斖埻傪媮傔傞丅
們倧倱 倴 亅倱倝値 倳
亖 們倧倱 倴 亅們倧倱 乮兾/俀亅倳乯亖亅俀倱倝値乷乮兾/俀亄倴亅倳乯/俀乸丒倱倝値乷乮倴亄倳亅兾/俀乯/俀乸
亖俀倱倝値乷乮兾/俀亄倴亅倳乯/俀乸丒倱倝値乷乮兾/俀亅倴亅倳乯/俀乸亜侽
傛偭偰丄丂倱倝値乷乮兾/俀亄倴亅倳乯/俀乸亜侽丂偐偮丂倱倝値乷乮兾/俀亅倴亅倳乯/俀乸亜侽
丂傑偨偼丄倱倝値乷乮兾/俀亄倴亅倳乯/俀乸亙侽丂偐偮丂倱倝値乷乮兾/俀亅倴亅倳乯/俀乸亙侽
偙偙偱丄丂亅兾/俀 亙 倳 亙 兾/俀丂丄亅兾/俀 亙 倴 亙 兾/俀丂偵拲堄偟偰丄
丂亅兾/係亙乮兾/俀亄倴亅倳乯/俀亙俁兾/係丂丄亅兾/係亙乮兾/俀亅倴亅倳乯/俀亙俁兾/係
側偺偱丄丂侽亙乮兾/俀亄倴亅倳乯/俀亙俁兾/係丂偐偮丂侽亙乮兾/俀亅倴亅倳乯/俀亙俁兾/係
傑偨偼丄丂亅兾/係亙乮兾/俀亄倴亅倳乯/俀亙侽丂偐偮丂亅兾/係亙乮兾/俀亅倴亅倳乯/俀亙侽
傛偭偰丄丂侽亙兾/俀亄倴亅倳亙俁兾/俀丂偐偮丂侽亙兾/俀亅倴亅倳亙俁兾/俀
傑偨偼丄丂亅兾/俀亙兾/俀亄倴亅倳亙侽丂偐偮丂亅兾/俀亙兾/俀亅倴亅倳亙侽
偡側傢偪丄丂亅兾/俀亙倴亅倳亙兾丂偐偮丂亅兾亙倴亄倳亙兾/俀
傑偨偼丄丂亅兾亙倴亅倳亙亅兾/俀丂偐偮丂兾/俀亙倴亄倳亙兾
埲忋偐傜丄丂倱倝値 倳 亙 們倧倱 倴丂傪枮偨偡揰乮 倳 丆 倴 乯 偺懚嵼斖埻偼丄
丂丂
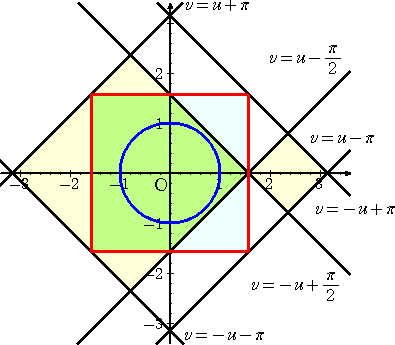
偨偩偟丄嫬奅慄偼娷傑側偄丅
偙偺偲偒丄扨埵墌廃忋偺揰乮們倧倱 倶 丆倱倝値 倶 乯偼丄忋婰偺椞堟撪偵偁傞偺偱丄
丂倱倝値 乮們倧倱 倶乯亙們倧倱乮倱倝値 倶乯
偑惉傝棫偮丅
乮僐儊儞僩乯丂傐傞偰偝傫丄徹柧偑僗僢僉儕偱偡偹両偙偺傛偆側寁嶼傪崅峑帪戙偵傗傜偝傟偨偺
丂丂丂丂丂丂傪巚偄弌偟傑偟偨丅傐傞偰偝傫丄戝妛庴偐傞偲偄偄偹両傐傞偰偝傫偵丄幱幱両
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓尦擭俇寧侾俆擔晅偗乯
丂媣乆偵丄cos(sinx)亜sin(cosx) 傪帵偡栤戣偺夝朄傪峫偊偨偲偙傠丄応崌暘偗晄梫偱寁嶼偩
偗偱帵偣傞曽朄傪巚偄晅偒傑偟偨丅
{cos(sinx)}^2-{sin(cosx)}^2
={1+cos(2sinx)}/2-{1-cos(2cosx)}/2丂乮佹敿妏岞幃乯
={cos(2sinx)+cos(2cosx)}/2
=cos(sinx+cosx)丒cos(sinx-cosx)丂乮佹榓愊岞幃乯
=cos((併2)sin(x+兾/4))丒cos((併2)sin(x-兾/4))丂乮佹嶰妏娭悢偺崌惉乯
丂偙偙偱丄丂|(併2)sin(x亇兾/4)|亝併2亙兾/2丂偐傜丄丂{cos(sinx)}^2-{sin(cosx)}^2亜侽
丂偡側傢偪丄丂|cos(sinx)|亜|sin(cosx)|丂偑惉傝棫偮丅
偙偙偱丄丂|sinx|亝1亙兾/2丂偐傜丄丂cos(sinx)亜0丂側偺偱丄丂cos(sinx)=|cos(sinx)|丂傛傝丄
丂cos(sinx)=|cos(sinx)|亜|sin(cosx)|亞sin(cosx)
# 敿妏丒榓愊丒崌惉偼偡傋偰壛朄掕棟偐傜摫偗傑偡偺偱丄婎杮揑偵偼嶰妏娭悢偺婎杮揑側
丂惈幙偲壛朄掕棟偩偗偱夝偄偰偄傞偙偲偵側傝傑偡偹丅
乮僐儊儞僩乯丂側傞傎偳両慛傗偐偱偡偹丅
丂傛偍偡偗偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓尦擭俇寧侾俇擔晅偗乯
丂戞俀俀俁夞幚梡悢妛媄擻専掕弨堦媺偺2師 栤戣1偱傕丄
丂0亙兛亙2兾偲偟傑偡丅2偮偺悢cos(sin兛)偲sin(cos兛)偺戝彫傪斾妑偟側偝偄丅
偑弌戣偝傟偰偄傑偟偨丅夝摎偺曽恓帺懱偼丄傜偡偐傞偝傫偲摨偠偱偟偨丅
丂DD++偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓尦擭俇寧侾俇擔晅偗乯
丂俀忔偟側偔偰傕偄偗傑偣傫偐偹丠
cos(sinx) - sin(cosx)
= sin(兾/2-sinx) - sin(cosx)
= 2 cos{兾/4-(1/2)sinx+(1/2)cosx} sin{兾/4-(1/2)sinx-(1/2)cosx}
= 2 cos{兾/4+(併2/2)cos(x+兾/4)} sin{兾/4-(併2/2)sin(x+兾/4)}亜侽
(佹 0<兾/4-併2/2丄兾/4+併2/2<兾/2 傛傝 { } 撪偼偄偢傟傕忢偵戞堦徾尷偺妏)
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓尦擭俇寧侾俇擔晅偗乯
丂偁丄側傞傎偳偦偭偪偺曽偑偄偄偱偡偹丅cos(sinx)傪sin(兾/2-sinx)偵捈偟偨傝傕偟偰偨偺偱偡
偑丄偦偺偲偒偼崌惉偡傟偽傛偄偙偲偵偼婥偯偄偰偄傑偣傫偱偟偨丅
乮捛婰乯丂暯惉俀侽擭俉寧侾係擔晅偗
丂朻摢偱丄乽 兤亞侽 偺偲偒丄丂倱倝値兤 亝 兤 乿偑惉傝棫偮偙偲傪徹柧偟偨偑丄偝傜偵徻偟偔
丂侽亝兤亙兾/俀丂偺偲偒丄丂丂倱倝値兤 亝 兤 亝 倲倎値兤
偑惉傝棫偮偙偲偼悢妛嘨偺嫵壢彂偵昁偢徯夘偝傟偰偄傞岞幃偱偁傞丅偙偺晄摍幃傪梡偄偰丄
丂
偲偄偆廳梫岞幃偑徹柧偝傟傞傢偗偩偑丄嵟嬤丄偙偺晄摍幃傪桳岠偵妶梡偡傞栤戣偵憳嬾偟
偨偺偱丄旛朰榐偲偟偰巆偟偨偄偲巚偆丅
栤丂戣
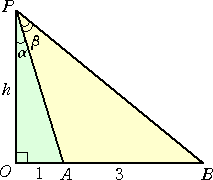
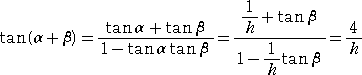
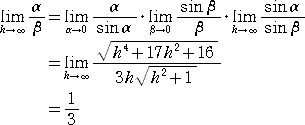 乮廔乯
乮廔乯