
三角形の内角の2等分線は、1点(内心)で交わる。これは初等幾何の有名な事実だろう。
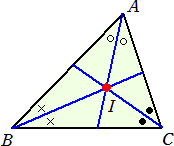
この「角の2等分」を「角の3等分」に言い換えて、定理の拡張を考えることはごく自然な発
想と思われる。
すなわち、
三角形の内角の3等分線を引くとき、隣り合う3等分線の交点が作る三角形は正三
角形になる
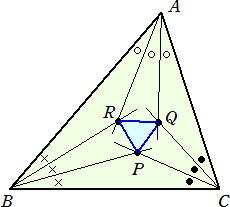
この定理は、1899年頃、アメリカの数学者 Frank Morley(1860〜1937)によって発見された。
図を描いてみると、確かに正三角形になりそうであるが、それを示すのは難しそうだ。
(→ 証明は、「複素数の底力」を参照)
以下、工事中!