
丂帺慠悢 倃 丄倄 丄倅 偵懳偟偰丄偦偺榓傪峫偊丄曽掱幃
丂丂丂丂丂倃亄倄亄倅亖俶丂乮俶偼丄梌偊傜傟偨帺慠悢乯
傪枮偨偡夝偺屄悢傪栤偆栤戣偼丄弴楍丒慻崌偣偺暘栰偱偼捖晠偲傕巚偊傞戣嵽偱偁傞丅
丂嵟嬤丄偙偺栤戣偵懳偟偰丄偙傟傑偱偺捠擮偵巋寖傪梌偊傞栤戣愝掕偵憳嬾偟偨偺偱丄偙
偺儁乕僕偱丄偦偺傑偲傔傪偟傛偆偲巚偆丅
丂捠忢丄忋婰偺栤戣傪夝偔応崌丄夝偺悢帤偺慻崌偣偑摨偠偱偁偭偰傕丄偦偺弴彉偑堎側傞
応崌偼堎側傞傕偺偲偟偰埖偆丅
丂偮傑傝丄偨偲偊偽丄曽掱幃丂倃亄倄亄倅亖俆丂偱丄
丂丂乮 倃 丆倄 丆倅 乯亖乮 俀 丆俀 丆侾 乯丂偲丂乮 倃 丆倄 丆倅 乯亖乮 俀 丆侾 丆俀 乯
偼堎側傞夝偺慻偲偟偰悢偊傞偲偄偆偙偲偱偁傞丅
丂崅峑帪戙偵梡偄偨嶲峫彂丒栤戣廤偱偼丄偙偺庬偺栤戣偵偼昁偢偲尵偭偰偄偄傎偳丄忋婰
偺傛偆側扐偟彂偒偑揧偊傜傟偰偄偨丅懡暘崱傕偦偆丏丏丏丅
丂偙傟傑偱丄偁傑傝婥偵傕棷傔側偐偭偨偑丄偙偺偙偲偼摉慠栤戣夝朄偵廳戝側塭嬁傪梌偊傞
晹暘偱偁傞丅嫲傜偔懡偔偺曽偼丄偦偺扐偟彂偒偱峫偊傞偙偲偼偛偔摉偨傝慜偺偙偲偲巚偭偰偄傞
偐傕偟傟側偄丅乮巹傕偦偆偱偟偨両乯
丂偨偩丄偙偺扐偟彂偒偼丄堦斒揑偵偼偡偛偔晄帺慠偵姶偠傞丅俁悢偺榓傪峫偊傞応崌丄椺偊
偽丄乽俁悢偺榓偑俆偵側傞応崌偼丠乿偲栤傢傟傟偽丄捠忢乽 俁丄侾丄侾丂傑偨偼丂俀丄俀丄侾乿偲摎
偊傞曽偑帺慠偩傠偆丅偙偺尒曽偼丄夝傪丄悢偺乽慻崌偣乿偲尒傞傕偺偱丄扐偟彂偒偑偁傞曽偼
夝傪丄悢偺乽弴楍乿偲尒傞傕偺偱偁傞丅
丂偙偺俀偮偺尒曽偱夝偺屄悢偑偳偆曄傢傞偐傪丄傑偢嬶懱椺偱妋偐傔偰傒傛偆丅
椺侾倎丂帺慠悢 倃 丄倄 丄倅 偵懳偟偰丄曽掱幃丂倃亄倄亄倅亖俁丂傪枮偨偡夝偺屄悢傪媮傔傛丅
乮夝乯丂乮 倃 丆倄 丆倅 乯亖乮 侾 丆侾 丆侾 乯丂偺 侾 捠傝偟偐側偄丅丂乮廔乯
椺侾倐丂俁偮偺帺慠悢偺榓偑俁偲側傞傛偆側応崌偺悢傪媮傔傛丅
乮夝乯丂乷 侾 丆侾 丆侾 乸丂偺 侾 捠傝偟偐側偄丅丂乮廔乯
椺俀倎丂帺慠悢 倃 丄倄 丄倅 偵懳偟偰丄曽掱幃丂倃亄倄亄倅亖係丂傪枮偨偡夝偺屄悢傪媮傔傛丅
乮夝乯丂乮 倃 丆倄 丆倅 乯亖乮 侾 丆侾 丆俀 乯丄乮 侾 丆俀 丆侾 乯丄乮 俀 丆侾 丆侾 乯丂偺 俁 捠傝丅丂乮廔乯
椺俀倐丂俁偮偺帺慠悢偺榓偑係偲側傞傛偆側応崌偺悢傪媮傔傛丅
乮夝乯丂乷 侾 丆侾 丆俀 乸丂偺 侾 捠傝偟偐側偄丅丂乮廔乯
椺俁倎丂帺慠悢 倃 丄倄 丄倅 偵懳偟偰丄曽掱幃丂倃亄倄亄倅亖俆丂傪枮偨偡夝偺屄悢傪媮傔傛丅
乮夝乯丂乮 倃 丆倄 丆倅 乯亖乮 侾 丆侾 丆俁 乯丄乮 侾 丆俀 丆俀 乯丄乮 侾 丆俁 丆侾 乯丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮 俀 丆侾 丆俀 乯丄乮 俀 丆俀 丆侾 乯丄乮 俁 丆侾 丆侾 乯丂偺 俇 捠傝丅丂乮廔乯
椺俁倐丂俁偮偺帺慠悢偺榓偑俆偲側傞傛偆側応崌偺悢傪媮傔傛丅
乮夝乯丂乷 侾 丆侾 丆俁 乸丄乷 侾 丆俀 丆俀 乸丂偺 俀 捠傝丅丂乮廔乯
椺係倎丂俁庬椶偺偍壻巕 倃 丄倄 丄倅 偑偦傟偧傟偨偔偝傫偁傝丄偙偺拞偐傜俇屄傪慖傃丄偍傗偮
丂丂丂丂僙僢僩傪嶌傞丅堎側傞偍傗偮僙僢僩偼壗庬椶偱偒傞偐丠 偨偩偟丄偳偺偍壻巕傕昁偢 侾
丂丂丂丂屄偼擖傟傞傕偺偲偡傞丅乮俫俀侽擭搙丂戝嵢懡杸拞妛丂擖帋栤戣傛傝夵戣乯
乮夝乯丂偙偺栤戣偼丄乽帺慠悢 倃 丄倄 丄倅 偵懳偟偰丄曽掱幃丂倃亄倄亄倅亖俇丂傪枮偨偡夝偺屄
丂丂丂悢傪媮傔傛丅乿偲慡偔摨偠偱偁傞丅摎偊偼丄
丂丂丂丂乮 倃 丆倄 丆倅 乯亖乮 侾 丆侾 丆係 乯丄乮 侾 丆俀 丆俁 乯丄乮 侾 丆俁 丆俀 乯丄乮 侾 丆係 丆侾 乯丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮 俀 丆侾 丆俁 乯丄乮 俀 丆俀 丆俀 乯丄乮 俀 丆俁 丆侾 乯丄乮 俁 丆侾 丆俀 乯丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮 俁 丆俀 丆侾 乯丄乮 係 丆侾 丆侾 乯丂丂偺 侾侽 捠傝丅丂乮廔乯
丂丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒
丂帺慠悢 倃 丄倄 丄倅 偵懳偟偰丄曽掱幃丂倃亄倄亄倅亖俶丂乮俶偼丄梌偊傜傟偨帺慠悢乯傪枮偨
偡夝偺屄悢偼丄堦斒揑偵丄廳暋慻崌偣偺峫偊傪梡偄偰夝偐傟傞丅
丂摉慠側偑傜丄丂俶亞俁丂偱丄梌幃傪丄丂乮倃亅侾乯亄乮倄亅侾乯亄乮倅亅侾乯亖俶亅俁丂偲曄宍偡傞丅
丂偙偺偲偒丄媮傔傞応崌偺悢偼丄憡堎側傞俁屄偺傕偺乷 倃亅侾丄倄亅侾丄倅亅侾 乸偐傜廳暋傪嫋
偟偰丄俶亅俁屄偲傞慻崌偣偺悢偵摍偟偄偺偱丄
丂丂丂丂丂丂丂3俫N-3亖N-1俠N-3亖N-1俠2亖(俶亅侾)(俶亅俀)/俀
偲側傞丅
丂丂俶亖俁丂偺偲偒丄丂(俶亅侾)(俶亅俀)/俀亖侾丂丒丒丒丒丒丂椺侾倎
丂丂俶亖係丂偺偲偒丄丂(俶亅侾)(俶亅俀)/俀亖俁丂丒丒丒丒丒丂椺俀倎
丂丂俶亖俆丂偺偲偒丄丂(俶亅侾)(俶亅俀)/俀亖俇丂丒丒丒丒丒丂椺俁倎
丂嵟嬤丄廳暋慻崌偣偵埶傜側偄暿夝偑偁傞偙偲傪抦偭偨丅
丂婎杮偲側傞岞幃偼丄
丂曽掱幃丂倃亄倄亖俲丂乮俲偼丄梌偊傜傟偨帺慠悢乯傪枮偨偡夝偺屄悢偼丄丂俲亅侾 屄
偲偄偆傕偺丅偙傟偼丄柧傜偐偲偟偰傕栤戣偼側偄偩傠偆丅
丂偙偺偲偒丄媮傔傞夝偺屄悢偼師偺傛偆偵寁嶼偝傟傞丅
丂丂丂丂
丂偙偺傛偆側岞幃傪梡偄傟偽丄椺*倎 偺僞僀僾偺栤戣偼姰慡偵夝偐傟傞丅
丂偦傟偵懳偟偰丄椺*倐 偺僞僀僾偺栤戣傪姰慡偵夝偔岞幃偼懚嵼偡傞偺偩傠偆偐丠
丂堦斒揑側岞幃傪峫偊傞偨傔偵丄
椺係倐 丗 乽俁偮偺帺慠悢偺榓偑俇偲側傞傛偆側応崌偺悢傪媮傔傛丅乿
偲偄偆栤戣傪丄晛曊揑側夝朄偲偄偆傕偺傪堄幆偟偰夝偄偰傒傛偆丅
丂戣堄傪枮偨偡帺慠悢 倃 丄倄 丄倅 偼丄
丂丂丂曽掱幃丂倃亄倄亄倅亖俇丂丂丄丂倃 亝 倄 亝 倅
傪枮偨偡傕偺偲峫偊偰傕堦斒惈傪幐傢側偄丅
丂偙偺偲偒丄嵟彫悢 倃 偼丄俁倃亝俇丂傛傝丄倃亝俀丂側偺偱丄庢傝摼傞抣偼丄侾 傑偨偼 俀 偲側傞丅
倃亖倠 乮 倠亖侾 傑偨偼 俀 乯 偺偲偒丄倄亄倅亖俇亅倠丂丄倄 亝 倅丂傪枮偨偡夝傪媮傔傟偽傛偄丅
倃 偺応崌偲摨條偵偟偰丄俀倄亝俇亅倠丂傛傝丄倠亝倄亝乮俇亅倠乯/俀丂偑丄帺慠悢 倄 偺庢傝摼傞抣
偱偁傞丅帺慠悢 倃 丄倄 偺抣偑掕傑傟偽丄曽掱幃丂倃亄倄亄倅亖俇丂傛傝丄帺慠悢 倅 偺抣偼帺
摦揑偵掕傑傞丅
丂倠亖侾丂偺偲偒丄丂侾亝倄亝俆/俀丂傛傝丄丂倄 亖 侾 丄 俀
丂倠亖俀丂偺偲偒丄丂俀亝倄亝俀丂傛傝丄丂倄 亖 俀
丂埲忋偐傜丄媮傔傞夝偺慻偼丄乷 侾 丆侾 丆係 乸丄乷 侾 丆俀 丆俁 乸丄乷 俀 丆俀 丆俀 乸丂偺 俁 捠傝丅
丂忋婰偺寁嶼傪怳傝曉偭偰傒傞偲丄帺慠悢 倎 傪帺慠悢 倐 偱妱偭偨偲偒偺彜傪媮傔傞昁梫
偑偁傞偙偲偑暘偐傞丅
丂偙偺寁嶼偵棙梡偝傟傞婰崋偑僈僂僗偺婰崋 乵倶乶 偱偁傞丅乮 仺 嶲峫丗乽僈僂僗偺婰崋乿乯
丂偙偙偱偼丄丂帺慠悢 倎 傪帺慠悢 倐 偱妱偭偨偲偒偺彜偼丄乵倎/倐乶
偲偄偆柧傜偐側帠幚傪妶梡偡傞偙偲偵偟傛偆丅
丂偙偺婰崋傪梡偄傞偲丄忋婰偺寁嶼偼丄師偺傛偆偵惍棟偝傟傞丅
丂戣堄傪枮偨偡帺慠悢 倃 丄倄 丄倅 偼丄
丂丂丂曽掱幃丂倃亄倄亄倅亖俇丂丂丄丂倃 亝 倄 亝 倅
傪枮偨偡傕偺偲峫偊偰傕堦斒惈傪幐傢側偄丅
丂偙偺偲偒丄嵟彫悢 倃 偼丄侾亝倃亝乵俇/俁乶亖俀丂側偺偱丄庢傝摼傞抣偼丄侾 傑偨偼 俀 偲側傞丅
倃亖倠 乮 倠亖侾 傑偨偼 俀 乯 偺偲偒丄倄亄倅亖俇亅倠丂丄倄 亝 倅丂傪枮偨偡夝傪媮傔傟偽傛偄丅
倃 偺応崌偲摨條偵偟偰丄帺慠悢 倄 偺庢傝摼傞抣偼丄丂倠亝倄亝乵乮俇亅倠乯/俀乶丂偱偁傞丅
帺慠悢 倃 丄倄 偺抣偑掕傑傟偽丄曽掱幃丂倃亄倄亄倅亖俇丂傛傝丄帺慠悢 倅 偺抣偼帺摦揑偵
掕傑傞丅
丂倠亖侾丂偺偲偒丄丂侾亝倄亝乵俆/俀乶亖俀丂傛傝丄丂倄 亖 侾 丄 俀
丂倠亖俀丂偺偲偒丄丂俀亝倄亝乽係/俀乶亖俀丂傛傝丄丂倄 亖 俀
丂埲忋偐傜丄媮傔傞夝偺慻偼丄乷 侾 丆侾 丆係 乸丄乷 侾 丆俀 丆俁 乸丄乷 俀 丆俀 丆俀 乸丂偺 俁 捠傝丅
丂偙偺傛偆偵峫偊傞偲丄堦斒揑偵丄帺慠悢 倃 丄倄 丄倅 偱丄
丂丂丂丂曽掱幃丂倃亄倄亄倅亖俶丂丄倃 亝 倄 亝 倅
傪枮偨偡夝偺屄悢傪悢偊傞偲偄偆夝朄偺巜恓偼柧妋偵棟夝偱偒傞偙偲偩傠偆丅
乮夝乯丂嵟彫悢 倃 偼丄侾亝倃亝乵俶/俁乶亖値丂側偺偱丄庢傝摼傞抣偼丄侾 埲忋 値 埲壓偺帺慠悢
丂丂丂偱偁傞丅
丂丂丂丂倃亖倠 乮 侾亝倠亝値 乯 偺偲偒丄 倄亄倅亖俶亅倠丂丄倄 亝 倅丂傪枮偨偡夝傪媮傔傟偽傛偄丅
丂丂倃 偺応崌偲摨條偵偟偰丄帺慠悢 倄 偺庢傝摼傞抣偼丄丂倠亝倄亝乵乮俶亅倠乯/俀乶亖倛倠丂傛傝丄
丂倛倠亅倠亄侾 捠傝偺応崌偑偁傞丅
丂丂帺慠悢 倃 丄倄 偺抣偑掕傑傟偽丄曽掱幃丂倃亄倄亄倅亖俶丂傛傝丄帺慠悢 倅 偺抣偼帺摦揑
丂偵掕傑傞丅
丂丂偟偨偑偭偰丄媮傔傞応崌偺悢偼丄
丂丂丂丂丂丂丂丂
丂偲側傞丅
丂丂偙偙偱丄丂俶亖俁値亄倰丂乮値 偼帺慠悢偱丄倰 偼丄侽 傑偨偼 侾 傑偨偼 俀乯偲偍偔偲丄
丂丂丂丂丂丂倛倠亖乵乮俶亅倠乯/俀乶亖乵乮俁値亄倰亅倠乯/俀乶
丂側偺偱丄忋婰偺榓偼丄
丂丂丂丂丂丂丂
丂偲曄宍偝傟傞丅
丂丂偲偙傠偱丄帺慠悢 倣 偵懳偟偰丄
丂丂丂丂丂倣 偑嬼悢側傜偽丄乵倣/俀乶亖倣/俀
丂丂丂丂丂倣 偑婏悢側傜偽丄乵倣/俀乶亖乮倣亅侾乯/俀亖倣/俀亅侾/俀
丂偱偁傞偺偱丄堦斒揑偵
丂丂丂丂丂丂丂丂丂
丂偲彂偔偙偲偑弌棃傞丅偙偺偲偒丄
丂
丂偱偁傞偺偱丄媮傔傞応崌偺悢偼丄
丂
丂偲側傞丅丂乮廔乯
丂偙偺岞幃傪
椺係倐 丗 乽俁偮偺帺慠悢偺榓偑俇偲側傞傛偆側応崌偺悢傪媮傔傛丅乿
偲偄偆栤戣偵揔梡偟偰傒傛偆丅
丂俇亖俁丒俀亄侽丂側偺偱丄値亖俀丄倰亖侽丂傪忋婰偺岞幃偵戙擖偡傞偲丄
丂丂梌幃亖乮俁丒俀2亄俀丒俀丒侽乯/係亄乮亅侾乯0乮侾亅乮亅侾乯2乯/俉亖俁
偲側傝丄愭偺寁嶼寢壥偲堦抳偡傞丅
丂忋婰偱岞幃側傞傕偺傪媮傔偨偑丄寛偟偰妎偊傗偡偄宍偵偼側偭偰偄側偄丅庒姳幃曄宍傪
帋傒偰妎偊傗偡偄宍偵偟傛偆丅
丂
偱偁傞偺偱丄
丂丂
偺嫇摦偑栤戣偲側傞丅
丂倰亖侽丂偺偲偒
丂丂
丂倰亖侾丂偺偲偒
丂丂
丂倰亖俀丂偺偲偒
丂丂
丂埲忋偐傜丄媮傔傞応崌偺悢偼丄
丂丂丂丂丂丂丂
偲側傞丅
椺俆倐丂俁偮偺帺慠悢偺榓偑俈偲側傞傛偆側応崌偺悢傪媮傔傛丅
乮夝乯丂忋婰偺岞幃傪梡偄傟偽丄
丂丂丂丂
丂偡側傢偪丄
丂丂丂丂
丂偲側傝丄媮傔傞応崌偺悢偼丄係偲側傞丅丂乮廔乯
丂幚嵺偵丄偦偺夝偺慻傪媮傔偰傒傟偽丄
丂丂乷 侾 丆侾 丆俆 乸丄乷 侾 丆俀 丆係 乸丄乷 侾 丆俁 丆俁 乸丄乷 俀 丆俀 丆俁 乸
偺係捠傝偱偁傞丅
丂偲偙傠偱丄戣堄傛傝丄
丂丂丂丂丂丂丂
偼昁偢懚嵼偟丄偟偐傕丄偨偩堦偮偱偁傞丅偙偺偙偲傪峫偊傞偲丄媮傔傞応崌偺悢偼丄娙扨偵丄
丂丂丂丂丂丂
偵嵟傕嬤偄帺慠悢偲偄偭偰傕傛偄偙偲偵婥偑偮偔丅
丂偄傑丄惍悢 倃 偵嵟傕嬤偄惍悢傪丄乮倃乯 偲昞偡偙偲偵偡傞丅
偡側傢偪丄丂倃亅乵倃乶亙侽丏俆丂側傜偽丄丂乮倃乯亖乵倃乶
丂丂丂丂丂丂丂倃亅乵倃乶亜侽丏俆丂側傜偽丄丂乮倃乯亖乵倃乶亄侾
丂丂乮拲堄乯丂乮倃乯偲偄偆婰崋偼丄倃亅乵倃乶亗侽丏俆丂偺応崌偵尷偭偰巊梡偝傟傞丅
丂偙偺婰崋傪妶梡偡傟偽丄帺慠悢 倃 丄倄 丄倅 偱丄曽掱幃丂倃亄倄亄倅亖俶丂丄倃 亝 倄 亝 倅
傪枮偨偡夝偺屄悢偼丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
偱梌偊傜傟傞丅
椺俇倐丂俁偮偺帺慠悢偺榓偑俉偲側傞傛偆側応崌偺悢傪媮傔傛丅
乮夝乯丂俉2/侾俀亖俇係/侾俀亖俆亄侾/俁丂偵嵟傕嬤偄帺慠悢偼丄俆 側偺偱丄
丂丂丂媮傔傞屄悢偼丄俆屄丂乮廔乯
丂幚嵺偵丄偦偺夝偺慻傪媮傔偰傒傟偽丄
丂丂乷 侾 丆侾 丆俇 乸丄乷 侾 丆俀 丆俆 乸丄乷 侾 丆俁 丆係 乸丄乷 俀 丆俀 丆係 乸丄乷 俀 丆俁 丆俁 乸
偺俆捠傝偱偁傞丅
丂忋婰偺寁嶼偱丄
椺侾倐丂俁偮偺帺慠悢偺榓偑俁偲側傞傛偆側応崌偺悢偼丄侾捠傝
椺俀倐丂俁偮偺帺慠悢偺榓偑係偲側傞傛偆側応崌偺悢偼丄侾捠傝
椺俁倐丂俁偮偺帺慠悢偺榓偑俆偲側傞傛偆側応崌偺悢偼丄俀捠傝
椺係倐丂俁偮偺帺慠悢偺榓偑俇偲側傞傛偆側応崌偺悢偼丄俁捠傝
椺俆倐丂俁偮偺帺慠悢偺榓偑俈偲側傞傛偆側応崌偺悢偼丄係捠傝
椺俇倐丂俁偮偺帺慠悢偺榓偑俉偲側傞傛偆側応崌偺悢偼丄俆捠傝
偲偄偆寢壥傪栚偵偡傞偲丄壗偲側偔
丂俶亞係 偱丄俁悢偺榓偑俶偲側傞応崌偺悢偼丄丂俶亅俁 捠傝乮丠乯
偲偄偆婜懸乮丠乯傪帩偨偝傟傞偑丄俶亖俋 偺応崌偵尒帠偵偦偺婜懸偼棤愗傜傟傞丅
丂幚嵺偵丄俋2/侾俀亖俉侾/侾俀亖俇亄俁/係丂偵嵟傕嬤偄帺慠悢偼丄俈 側偺偱丄俁偮偺帺慠悢偺
榓偑俋偲側傞傛偆側応崌偺悢偼丄俈 捠傝偱偁傝丄俇 捠傝偱偼側偄両
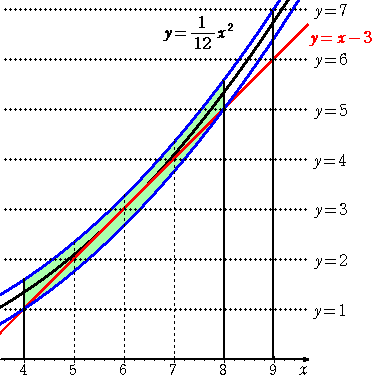
丂丂丂嵍恾偐傜丄
丂丂丂丂倷亖乮侾/侾俀乯倶2
丂丂丂丂倷亖倶亅俁
丂丂偲偄偆俀偮偺僌儔僼偺愙嬤偡傞
丂丂條巕偑偆偐偑偊傞丅
丂偙偺俁悢偺榓偺栤戣偼丄師偺傛偆側栤戣偲傕摨摍偱偁傞丅
丂丂惓俶妏宍偺捀揰傪俁偮慖傫偱偱偒傞嶰妏宍偺憤悢偼偄偔偮偁傞偐丠
丂偨偩偟丄崌摨側傕偺偼嬫暿偟側偄傕偺偲偡傞丅
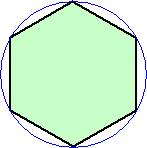
丂丂丂嵍恾偺傛偆偵丄惓俶妏宍偼墌偵撪愙偟偰偄傞丅惓俶妏宍偺俶屄
丂丂偺捀揰偱丄墌廃偼俶摍暘偝傟傞丅俀偮偺捀揰傪寢傇尫偼丄偄偔偮
丂丂偐偺摍暘偝傟偨墌屖偵傛傝嶌傜傟傞丅
丂俁偮偺帺慠悢偺榓偑俶偲側傞傛偆側応崌偺悢偼丄曽掱幃丂倃亄倄亄倅亖俶丂丄倃 亝 倄 亝 倅
傪枮偨偡帺慠悢 倃 丄倄 丄倅 偺慻偺悢偱偁傝丄偙偺 倃 丄倄 丄倅 偺抣偑偦傟偧傟墌屖偺悢傪
昞偡丅
丂俶亖俇丂偺偲偒丄偦偺夝偼丄乷 侾 丆侾 丆係 乸丄乷 侾 丆俀 丆俁 乸丄乷 俀 丆俀 丆俀 乸丂偺 俁 捠傝偱偁
偭偨偑丄偙傟傜偺応崌偼丄師偺傛偆側恾宍偲侾懳侾偵懳墳偡傞丅
丂丂
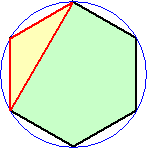 丂丂丂
丂丂丂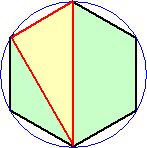 丂丂丂
丂丂丂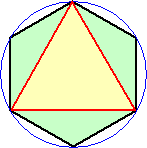
丂偙偺傛偆側帇揰偱悢妛傪峫偊傞偲丄師偺傛偆側堦尒擄偟偦偆側栤戣傕堈偟偔尒偊傞偙偲偩傠偆丅
栤丂戣丂丂惓廫妏宍偺捀揰傪俁偮慖傫偱偱偒傞嶰妏宍偺憤悢偼偄偔偮偁傞偐丠
丂丂丂丂丂偨偩偟丄崌摨側傕偺偼嬫暿偟側偄傕偺偲偡傞丅
乮夝乯丂侾侽2/侾俀亖侾侽侽/侾俀亖俉亄侾/俁丂偵嵟傕嬤偄帺慠悢偼丄俉 側偺偱丄媮傔傞応崌偺悢偼丄
丂丂丂俉 屄偱偁傞丅丂乮廔乯
乮嶲峫暥專丗丂傾丒儎僌儘儉丄僀丒儎僌儘儉丂挊丂摏堜岶堺丂栿
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 弶摍揑偵夝偄偨崅摍悢妛偺栤戣乮嘥乯丂丂乮搶嫗恾彂乯
丂丂丂丂丂丂丂丂崻忋惗栫丄拞杮撝峗丂挊丂丂婎慴悢妛椡僩儗乕僯儞僌丂丂乮擔杮昡榑幮乯乯