意外なところに正三角形　　　　　　　　　　　　　　　　　

　次の図形をご覧下さい。
　　　　　　

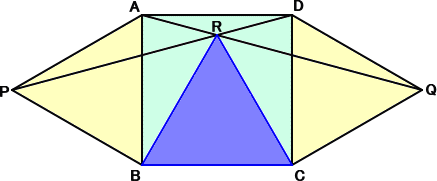
　１枚の正方形の左右に正三角形が張り出しています。このとき、上図のように２つの頂点
を結んでできる交点(Ｒ)は、正三角形（△ＲＢＣ）の１つの頂点になります。

　いろいろな道具（数学上の公式等）を用いると、その証明は簡単にできますが、中学校３年
レベルで（しかも、初等幾何で！）解答しようとすると、思いのほか難しいようです。

　「易しい（？）問題は易しく、図形の問題は図形で！」というのが私の信条ですが、ここは敢
えて批判を覚悟して、強引に証明したいと思います。

（解 １ ）・・・・・ 三角関数を用いる方法（正方形の１辺の長さを、２ とする。）

　　　点 Ｒ より、辺 ＡＤ に垂線 ＲＨ を下ろす。このとき、

　　　∠ＲＤＨ＝（１８０°−∠ＰＡＢ−∠ＢＡＤ）/２＝（１８０°−６０°−９０°）/２＝１５°

よって、
　　

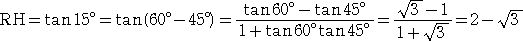
したがって、△ＲＢＣ は、底辺の長さが ２ の二等辺三角形で、高さは、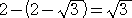

よって、△ＲＢＣ は、正三角形となる。


　上記では簡便に加法定理を用いてＲＨの長さを求めているが、全然中学生的ではない。
相似比を利用した解答も可能である。別解を、ｔｗｏ‐ｗｅｌｌさんから頂いた。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成１６年３月１０日付け）

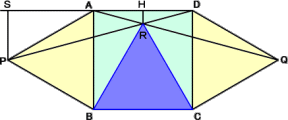左図において、ＡＢ＝２　とすると、 　　ＰＳ＝ＨＤ＝１、ＡＳ＝　である。 △ＰＳＤ∽△ＲＨＤ より、＋２ ： １＝１ ： ＲＨ 　よって、ＲＨ＝２−

　　　　　　　　　　　以下（解 １ ）と同様にして、△ＲＢＣ は、正三角形となる。

（解 ２ ）・・・・・ 座標幾何を用いる方法（正方形の１辺の長さを、２ とする。）

　Ｂ(０，０) を原点とし、ＢＣ を Ｘ 軸、ＢＡ を Ｙ 軸とする。このとき、

　　Ａ(０，２) 、Ｃ(２，０) 、Ｄ(２，２) 、Ｐ(−，１) 、Ｑ(２＋，１)

となる。直線 ＰＤ 、直線 ＱＡ の方程式は、それぞれ

　　Ｙ＝(２−)Ｘ−２＋２　、　Ｙ＝−(２−)Ｘ＋２

である。これらを連立して、交点 Ｒ の座標を求めれば、　（ １ ， ）

　したがって、△ＲＢＣ は、正三角形となる。

（解 ３ ）・・・・・ 図形を用いる方法（直接的な証明でないところが、少し心苦しい！）

　　　　　

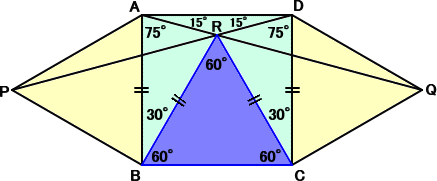
　冒頭の図において、△ＲＡＤ が、底角が １５°の二等辺三角形であることは明らか。その

三角形の１つの頂点として、点 Ｒ が唯一つ存在する。

　ところで、△ＲＢＣ が、正三角形と仮定すると、上図のような計算から、△ＲＡＤ は、底角が

１５°の二等辺三角形になる。

以上から、冒頭のように定まる点 Ｒ を用いた△ＲＢＣ は、正三角形でしかあり得ない。

（このような証明の気持ちの悪さは、実は、当ホームページの

　　お茶の時間　クイズ＆パズル　「正方形を重ねる」

においても経験される。）

　もう少し直接的な証明で、初等幾何を用いた中学３年レベルの証明がないかどうか、現在、
思案中である。もし、証明を発見された方、よかったら塾長宛メールをお願いします。

（参考ホームページ：飛行船すうがく　「小学生に説明するには難しい問題」）

（追記）　ｓｏｕｐ＆ｂｒｅａｄ　さんから、初等幾何的証明をお教えいただいた。まさに私の欲して
　　　　いた証明方法で、思わず、その巧妙さに感動してしまった。おかげさまで、何となく残っ
　　　　ていた証明の気持ちの悪さを払拭することができ、気分は爽快である。ｓｏｕｐ＆ｂｒｅａｄ
　　　　さんに感謝いたします。

　ｓｏｕｐ＆ｂｒｅａｄ　さんによれば、中学時代に通っていた塾で類似の問題に出会ったことがあ
るとか。ｓｏｕｐ＆ｂｒｅａｄ　さんも、その解法の巧妙さに、「ズルい！」って思われたそうです。

　それでは、ｓｏｕｐ＆ｂｒｅａｄ　さんの解答を一部補足して紹介したいと思います。

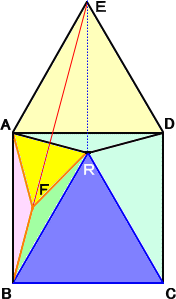図の設定は、上記の通りとする。 　　辺ＡＤ上に正三角形ＥＡＤを描く。（解１）と同様な計算をして、 ∠ＥＢＡ＝１５°である。 　　線分ＢＥ上に、点Ｆを、∠ＢＡＦ＝１５°であるようにとる。 　　このとき、明らかに、△ＡＢＦ≡△ＡＤＲ　なので、ＡＦ＝ＡＲ　と 　なる。さらに、∠ＦＡＲ＝６０°なので、△ＡＦＲは正三角形となる。 　よって、ＦＡ＝ＦＲ、∠ＡＦＢ＝∠ＲＦＢ（＝１５０°）、ＢＦ共通 　により、△ＡＢＦ≡△ＲＢＦ　となり、ＡＢ＝ＲＢ　である。 　　同様にして、ＤＣ＝ＲＣ　も示される。 　　従って、△ＲＢＣは、正三角形となる。

（コメント）　ｓｏｕｐ＆ｂｒｅａｄ　さんの解答でも、「意外なところに正三角形」が本質的に用いら
　　　　　　れているわけで、まさに、このページのタイトルの趣旨にあった解法ですね！

（追記）　Ｈ．Ｔ　さんから、円周角の性質を用いる初等幾何的証明をメールで頂いた。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成１７年６月１７日付け）

　お教えいただいた証明は、中学生的で技巧的なところは全くなく、非常に素直な解答に、
思わず感動してしまった。　Ｈ．Ｔ　さんに感謝いたします。

　それでは、Ｈ．Ｔ　さんの解答を一部補足して紹介したいと思います。

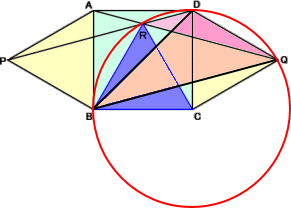△ＲＡＤの底角は、１５°なので、∠ＤＲＱ＝３０° また、∠ＤＢＱ＝∠ＤＢＣ−∠ＱＢＣ 　　　　　　　　＝４５°−１５°＝３０° 　　よって、∠ＤＲＱ＝∠ＤＢＱ 　　したがって、４点 Ｄ、Ｒ、Ｂ、Ｑ は同一円周上。 　３点 Ｄ、Ｂ、Ｑ を通る円はただ一つ定まり、３ 　点から等距離にある点 Ｃ がその円の中心と なる。

　　したがって、　ＢＣ＝ＲＣ　が成り立ち、同様にして、ＢＣ＝ＲＢ　もいえる。

　　以上から、△ＲＢＣは正三角形となる。


（追記）　さらに、Ｈ．Ｔ　さんから、上記の解の改良版（角度を用いない方法）をメールで頂い
　　　　　た。（平成１７年６月２４日付け）

　上図において、 点 Ｃ を中心として、Ｂ、Ｄ、Ｑ を通る円が一つ書ける。ＡＤは、この円の接

線となる。ここで、△ＡＰＤと△ＤＡＱは合同な二等辺三角形なので、∠ＡＤＲ＝∠ＤＱＲ

　よって、接弦定理が成り立ち、Ｒはこの円周上の点になる。

したがって、　ＲＣ＝ＢＣ　が成り立つ。同様にして、ＲＢ＝ＢＣ　なので、△ＲＢＣは正三角形。


（コメント）　冒頭の解析的証明に比べて、とても分かりやすい証明になっています。いろいろ
　　　　　　な証明があることに我ながら感動しています。Ｈ．Ｔ　さんに感謝いたします。

（追記）　当ＨＰがいつもお世話になっているＨＮ「らすかる」さんから「ほとんど自明」という感
　　　　じの証明方法を得たというメールを頂いた。（平成１７年６月２６日付け）

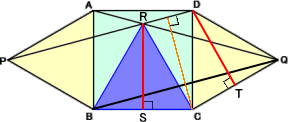△CQBは二等辺三角形で、PDとBQは平行。 △DCQをBQの垂直二等分線(Cを通る)に関し て対称移動すると、QはBに移り、CQの垂直二 等分線と直線PDの交点である点Dは、CBの垂 直二等分線と直線PDの交点である点Rに移る。

　従って、△DCQ≡△RCBなので、△RCBは正三角形となる。


（コメント）　線対称ということを使うと鮮やかですね！見てすぐ理解でき、十分初等的な証明
　　　　　　だと思います。らすかるさんに、感謝いたします。

（追記）　平成１７年１０月１０日付けで、Ｈ．Ｈ さんから、１年半ぶりにメールを頂いた。昨日
　　　　久々にこの問題について考えてみたところ、急に証明を思いつかれたとのことである。

　Ｈ．Ｈ さんの証明を掲載する前に、まずは謝罪から。

　上記の（解 １）では相似比を利用した解答も可能であるということで、ｔｗｏ‐ｗｅｌｌ さんからの
別解（平成１６年３月１０日付け）を載せたが、実は、Ｈ．Ｈ さんからも別解と同様のものを頂
いていた。（平成１６年２月９日付け）　その際は、（解 １）と同趣旨ということで掲載を見あわ
せたが、別解を載せた以上、Ｈ．Ｈ さんの別解についても触れなければいけなかったと反省
しています。この件について、当ＨＰへのアップが遅れたことを、Ｈ．Ｈ さんにお詫びしなけれ
ばならない。誠に申し訳ないです。

　頂いた証明は、趣旨を損なわない範囲で多少加筆・修正させていただきました。ご了承く
ださい。

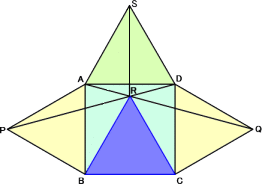（証明）　左図のように辺ＡＤ上に正三角形ＡＤＳを 　作る。このとき、△ＲＡＤは二等辺三角形なので、 　線分ＳＲは辺ＡＤの垂直二等分線となる。 　よって、線分ＡＢと線分ＳＲは平行。 　さらに、∠ＳＡＲ＝７５°、∠ＡＳＲ＝３０°より、 　∠ＳＲＡ＝７５°である。

　よって、△ＳＡＲは二等辺三角形となり、ＳＡ＝ＳＲ　となる。ここで、ＳＡ＝ＡＤ＝ＡＢ　なので、

ＡＢ＝ＳＲ　が成り立つ。

　以上から、四角形ＳＡＢＲは平行四辺形となり、ＳＡ＝ＲＢ　即ち、ＲＢ＝ＢＣ　が言える。

同様にして、ＳＤ＝ＲＣ　即ち、ＲＣ＝ＢＣとなり、ＲＢ＝ＢＣ＝ＲＣ　が成り立つ。

　したがって、△ＲＢＣは正三角形である。（証終）


（コメント）　なるほど！辺ＡＤ上に正三角形を作るところは、「意外なところに正三角形」の趣
　　　　　　旨に合致する解法ですね。平行四辺形の性質を利用した証明で、中学生にとって
　　　　　　も分かりやすい素晴らしい証明だと思います。Ｈ．Ｈ さんに感謝いたします。


（追記）　当ＨＰ読者のＨＮ「南東亜北西」さんから「私も考えてみました。」というメールを頂い
　　　　　た。（平成２８年９月２２日付け）

（証明の概略）　底辺をＢＣとする正三角形の頂点ＳがＲと一致することを導きます。

　直角二等辺三角形ＢＣＤをＣを中心に６０度回転させます。ＤはＱに移動し、ＢはＳに移動

します。∠ＣＱＡ＝４５°なので、ＳはＡＱ上にあります。同様に、ＳはＰＤ上にある事も言えま

す。よって、Ｓは、ＡＱとＰＤの交点であるＲと一致し、△ＲＢＣは正三角形となります。


（コメント）　なるほど、簡明な証明ですね！南東亜北西さんに感謝します。


　ＫＳさんから新しい視点をご教示いただきました。（平成２８年９月２２日付け）

　長方形ＡＢＣＤの外側に、ＡＢとＡＤを一辺とする正三角形をつくる。外側の点をＰ、Ｑとする

と、△ＰＱＣは正三角形となる。

　実際に、辺ＰＱ、辺ＰＣ、辺ＱＣを含む三角形が合同であることからわかります。


　カルピスさんからのコメントです。（平成２８年９月２２日付け）

　あ、ホントだ。本日は「秋分の日」。これを『秋分の大三角形』と呼ぼう♪


（コメント）　そこにも正三角形が作れるんですね！ＰＣ＝ＱＣ、∠ＰＱＣ＝６０°からも明らか
　　　　　　ですね。ＫＳさんに感謝します。


　ＫＳさんからの続報です。（平成２８年９月２３日付け）

　四角形の内側に折っても小さな正三角形が生まれる。四角形を平行四角形にしても成り
立つ。


　ＫＳさんからの続報です。（平成２８年９月２４日付け）

　任意の△ＡＢＣに対し、辺の外側に正三角形をつくり、その中心を結ぶと正三角形が
できる

　また、有名なモーリ―の定理では、

　三角形の３つの内角の３等分線の、辺に近い２つずつの交点は、正三角形の頂点を
なす


　DD++さんからのコメントです。（平成２８年９月２４日付け）

　前半は、ナポレオンの定理ですね。


　ＫＳさんからの続報です。（平成２８年９月２６日付け）

　三角形ＡＢＣのＡＢ、ＡＣの辺をもつ正三角形を外側につくり、その頂点をＤ、Ｅする。
ＡＤ、ＡＥを持つ平行四辺形をつくり、交点をＦとする。この時、ＦＢＣは正三角形になる。
　ただし、角Ａは６０度でないとする。

　意外性からいうと、モーリーの定理のように、最初に正三角形を作図しないで、結果として
正三角形が生まれるようなものは、他にありませんでしょうか？