同じ大きさの２枚の正方形がある。１つの正方形の上に、もう一方の正方形を任意に重
ねる。ただし、各辺は互いに２点で交わるものとする。
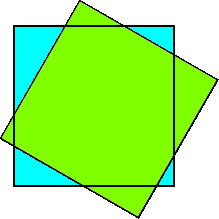
このとき、この正方形上の１点に針を刺して、その点の周りに２枚の正方形を回転させる
と、ぴったり重なるという。このような点を求めよ。
（答） 次のような点が求めるものである。
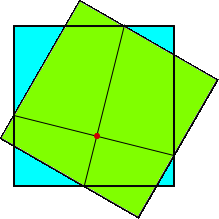
（参考文献：田村三郎 著 数学パズルランド （講談社））
（追記） 上記の点の求め方を検証してみよう。
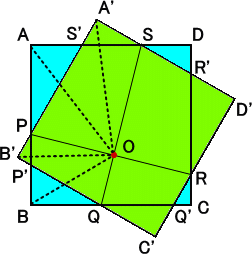このような点Ｏが存在したものとする。このとき、△ＡＯＢ と △Ａ’ＯＢ’において、
ＯＡ＝ＯＡ’
ＯＢ＝ＯＢ’
ＡＢ＝Ａ’Ｂ’
したがって、
△ＡＯＢ ≡ △Ａ’ＯＢ’
よって、
∠ＯＡＰ＝∠ＯＡ’Ｐ
このとき、
４点 Ｏ、Ａ、Ａ’、Ｐ は同一円周上にある。
ところで、
∠ＳＡＰ＝∠ＳＡ’Ｐ＝∠Ｒ
より、
４点 Ｓ、Ａ、Ａ’、Ｐ は同一円周上にある。
一つの円は、３点で唯一つに定まるので、２つの円は同じ円である。
したがって、５点 Ｏ、Ｓ、Ａ、Ａ’、Ｐ は同一円周上にある。
円に内接する四角形 ＯＳＡ’Ｐ において、
∠ＳＡ’Ｐ＝∠Ｒ なので、∠ＳＯＰ＝∠Ｒ
同様にして、∠ＰＯＱ＝∠ＱＯＲ＝∠ＲＯＳ＝∠Ｒ であることが分かる。
よって、３点 Ｐ、Ｏ、Ｒ かつ ３点 Ｓ、Ｏ、Ｑ は一直線上にあるので、点 Ｏ は、２直線ＰＲ
とＳＱの交点となる。