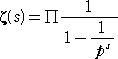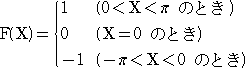���������̊��p�@�@ �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�u���������v�Ƃ́A�����I�ɂ́u�����̂��̂�����Ȃ�������v���Ƃ������B
�@���̂悤�ȃA�C�f�A�͌Â�������ɂ���A�a�D�b�D�R���I���A�A���L���f�X���A�������ƒ���
�ň͂܂ꂽ�����̖ʐς��A�����̎O�p�`�̖ʐς̘a�Ƃ��ċ��߂��Ƃ����b�͂悭�m���
����B
�@�������A�ߑ�Ɏ���܂ŁA���́u�����v�Ƃ������̂́A���w�ҒB�ɂ���Čh������Ă����B
�@�u�����v�Ƃ������̂��A���w�̊T�O�Ƃ��ď��߂ĂƂ炦���̂́A�J���g�[��(1845�`1918)��
����B
�@�f�f�L���g��J���g�[����̌����ɂ���āA�����̗��_���ł��A�����������܂߂�����
�ϕ��w���m�ł�����̂ɂȂ����̂́A�P�X���I���㔼�ɂȂ��Ă���̂��Ƃł���B
�@���̃y�[�W�ł́A��͊w�̊�b�Ƃ������閳�������ɂ��Ă��낢�뒲�ׂ悤�Ǝv���B
�@���� �o ���� �p �ɑ��āA�� �� �����a�@�r������1�{��2�{��3�{�E�E�E�{�����@�Ƃ����B
| ���� �o �r�� �p ����������Ƃ��A�������� |
�@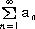 |
�@�����������Ƃ����A |
�@�@�@�@�@�@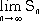 |
���r�@�Ȃ�A |
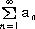 |
���r |
| �ł���B�@�r���A���������̘a�Ƃ����B |
�@�������������Ȃ��Ƃ��A���U�����Ƃ����B
��@��������
�@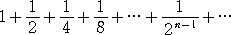
�̎����E���U�ׁA��������Ƃ��͘a�����߂�B
�@�� �� �����a�@�r�����P�{1/2�{1/4�{�E�E�E�{1/2��-1���Q(�P�|(1/2)��)�@�Ȃ̂ŁA���� �o �r�� �p
�͎������A�� �� ���@�̂Ƃ��A�r�� �� �Q�@�ł���B
�@���������āA���������͎������A���̘a�́A�Q �ł���B
�i���Ӂj�@�r���{1/2��-1�@�������v�Z���āA�r���{1/2��-1���Q�@�������Ă��悢�B
�@��L�̂��Ƃ́A���̂悤�ɐ}��������A�Ɍ��̌v�Z��m��Ȃ��Ă��[���ł��邾�낤�B
�@
�@��L�̖��������́A�������䋉���i�����j�Ƃ�����B
�藝�@���� ���A���� �� �̖������䋉���@���{�����{����2�{�E�E�E�{������-1�{�E�E�E�@�́A
�@�����O�@�܂��́@�|�P�������P�@�̂Ƃ��A�������A���̘a�́A��/(�P�|��)�@�ŗ^������B
��@���������i���a�����j
�@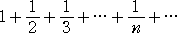
�͔��U����B
�@���̏ؖ��͎�X�l�����邪�A���l�I�ɂ͎��̏ؖ����ł��Ȗ����Ǝv���B
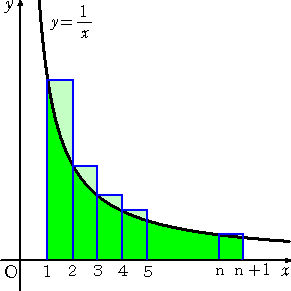 |
�@�@���}�ɂ����āA�� �� �����a
�@�@�r�����P�{1/2�{1/3�{�E�E�E�{1/n
�@���A����̒����`�̖ʐς̘a�ƍl����ƁA
�@�@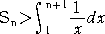
�@�@�����藧�B�@
�@�@����āA�r����������(���{�P)�@�ƂȂ�A
�@�@���� �o �r�� �p �͔��U����B
|
�@����ɑ��āA���g�o�����������b�ɂȂ��Ă���g�m�u�����S�R�v���A�a�V�ȏؖ��@�ɑ�
�����ꂽ�Ƃ̂��Ƃł���B�i�����Q�P�N�V���P�S���t���j
�@�܂��A�@�P ���傫�����R�� �� �ɑ��āA
�@�P/���{�P/�i���{�P�j�{�P/�i���{�Q�j�{�E�E�E�{�P/��2���P
�����藧�B
�@���ۂɁA�@�����Q�@�̂Ƃ��A
�@�P/���{�P/�i���{�P�j�{�P/�i���{�Q�j�{�E�E�E�{�P/��2���P/�Q�{�P/�R�{�P/�S���P�R/�P�Q���P
�����藧�B����ɁA�@�����R�̂Ƃ��A
�P/���{�P/�i���{�P�j�{�P/�i���{�Q�j�{�E�E�E�{�P/��2
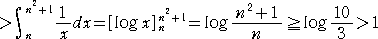
����āA�s�����͐��藧�B�@���̂Ƃ��A
�P�{�P/�Q�{�P/�R�{�P/�S�{�P/�T�{�P/�U�{�P/�V�{�P/�W�{�P/�X�{�E�E�E�E�E�E�E
���P�{�i�P/�Q�{�P/�R�{�P/�S�j�{�i�P/�T�{�P/�U�{�E�E�E�{�P/�Q�T�j
�@�@�{�i�P/�Q�U�{�P/�Q�V�{�E�E�E�{�P/�U�V�U�j�{�E�E�E�E
���P�{�P�{�P�{�P�{�E�E�E
����A���a���������U���邱�Ƃ�������B
�i�R�����g�j�@���̉�@�́A
�@�P�{�P/�Q�{�P/�R�{�P/�S�{�P/�T�{�P/�U�{�P/�V�{�P/�W�{�P/�X�{�E�E�E�E�E�E�E
���P�{�P/�Q�{�i�P/�R�{�P/�S�j�{�i�P/�T�{�P/�U�{�P/�V�{�P/�W�j�{�E�E�E�E�E�E�E
���P�{�P/�Q�{�i�P/�S�{�P/�S�j�{�i�P/�W�{�P/�W�{�P/�W�{�P/�W�j�{�E�E�E�E�E�E�E
���P�{�P/�Q�{�P/�Q�{�P/�Q�{�E�E�E�E�E�E�E
���甭�U���������@�Ɠ������������܂��ˁI�����S�R����Ɋ��ӂ��܂��B
�@��L�̂悤�Ȗ�����������ʉ����āA�[�[�^�� �āi���j����`�����B
�@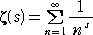
�藝�@�āi���j �́A�����P�@�̂Ƃ��������A�����P�@�̂Ƃ����U����B
�@�ؖ��́A��L�ŗp�������̂Ɠ��l�Ȋ��@�����P/�����@�ɂ��ē��l�ȍl�@���s���悢�B
���������āA�āi���j �� �� �̊��Ƃ��ĈӖ������̂́A�����P�@�̂Ƃ��ł���B
�@���������ɑ��āA���̎����E���U�ׂ邱�Ƃ͔�r�I�e�Ղł���B
�@�i�R�[�V�[�̔���@�A�_�����x�[���̔���@�Ȃǂ��m���Ă���B�j
�@����ɑ��āA�����������������邱�Ƃ��������Ă��A���ۂɂ��̘a�����߂邱�Ƃ͔��
�ɓ���B
�@�I�C���[�́A��S�̖��ɂ悤�₭�A�P�V�R�T�N����@ �āi�Q�j��(1/6)��2�@�ł��邱�Ƃ����B
����ɁA�āi�S�j��(1/90)��4�A�āi�U�j��(1/945)��6�@�ł��邱�Ƃ������Ă���B
�@�[�[�^�����A�~�����Ɗ֘A�Â����킯�ŁA�ƂĂ�����I�Ȏ��ƂȂ��Ă���B
�i�R�����g�j�@�~���� �� �Ɗ֘A�������������̔����́A�I�C���[���ŏ��ł͂Ȃ��B
�@�P�U�V�R�N�ɁA���C�v�j�b�c���A���̎������Ă���B
�@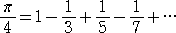
�@�܂��A���̎��́A���C�v�j�b�c����������O�ɁA�O���S���[�ɂ���Ĕ�������Ă����Ƃ�����
���B������Â��A�P�S�O�O�N���̃C���h�̐��w�҂ɂ���Ă����o����Ă����炵���B
�@�āi�Q�j��(1/6)��2�@�ɂ���A��L�̋����ɂ���A�~�����Ƃ͖��W�Ƃ��v���閳��������
�˔@�A�~�������W���Ă���Ƃ��������́A�ƂĂ�����I�Ȃ��Ƃł��邪�A���ۂɁA��L�̋�
���̍ŏ��̉��������Ƃ��ĉ~�����̋ߎ��l�����Ƃ߂�Ƃ������p�I�Ȗʂł́A��L�̖�����
���̉���������͂ł���B�������������ɖ��Œx���̂ł���B�~�����̋ߎ��l�̌v�Z�ɂ́A
�ʂ̍H�v���Ȃ���Ă���悤���B
�@�܂��A�[�[�^���́A�f���Ƃ��W�Â�����B
�@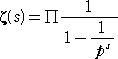 |
�@�@�@�������A�� �͑S�Ă̑f�����B�@ |
�@��L�ɂ����āA���a�����͔��U�������A���͂��̂��Ƃ���A�f���������ɁA����������
���z���Ă���Ƃ������Ƃ��A��L�̎���p���Ď������Ƃ��ł���B
�@����ȊO�ɂ��A�[�[�^���́A���낢��Ȑ��_�I�ȈӖ��������Ă��āA���̉��͐[���B
�i�NjL�j�@�����Q�P�N�P�P���Q�O���t��
�@�P�P���P�T���̖�X������m�g�j�����s�u�ŁA�u�����̓��`���[�}���\�z�E�V�˂����̓����`�v
�����f���ꂽ�BNHK�ł͉ߋ��ɁA�u�t�F���}�[�̗\�z�̉����v��u�|�A���J���\�z�̉����v��
�ǂɂ��ăR���p�N�g�ɕ�����₷���������ꂽ�ԑg����Ă������A����́A�܂�����
���Ƃ������Ƃ�����A����̗D�G�Ȑ��w�҂��ʊ��ɒ��킷����S�Ē��˕Ԃ���A�ߑs������
�Y�����e�ł������B���ɂ͐��_���a��ł��܂�������������Ƃ������Ƃł������܂�Ȃ��C
�����ɂȂ����B
�@���C�E�h�E�u�����W�����m�ɂ��ƁA���[�}���\�z�́u�l�ނɂƂ��čł�����A�ł��d�v�Ȓ�
���v���Ƃ����B
�@���[�}���\�z�i�P�W�T�X�N�j�Ƃ́A
�@�āi���j �̔���_�͑S�Ē��� �q���i���j��1/2 ��ɂ���
�Ƃ������̂ł���B�������A���̃āi���j �͏�L�Œ�`�������̂f���ʂɉ�͐ڑ�������
�̂Ƃ���B�����|2�A�|�S�A�E�E�E�@�͎�����_�ƌ�����B
�@����ȏ�[�[�^���ɗ������邱�Ƃ́A���g�o�̃��x�����͂邩�ɉz���Ă��܂��̂ŁA��
�ׂ͕ʂ̃y�[�W�ɏ��邱�Ƃɂ���B�����ł́A���̃y�[�W�̂��������̖ڕW�F
�@�w�@�t�[���G������p���āA�āi�Q�j��(1/6)��2�@�������@�x
�Ɉڂ肽���Ǝv���B
�@�ʏ�A�āi�Q�j��(1/6)��2�@�ł��邱�Ƃ́A������ς�p���Ď������B�i���@�Q�l�j
�@���l�I�ɂ́A������ςɂ��ؖ��́A���܂肵�����肱�Ȃ��B�ŋ߁A�t�[���G������p
����Ȗ��ȏؖ���m�肦���̂ŁA�Љ�����Ǝv���B
�t�[���G�����i�e�����������@�r�����������j
�@���� �Q�� �̘A���� �e(�w) �ɑ��āA�t�[���G�W�� �����@�A���� ���A�����ɂ���`����B
�@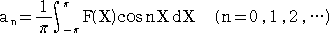
�@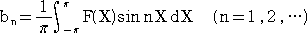
�@���̂Ƃ��A�O�p����
�@
���A�� �e(�w) ���t�[���G�����Ƃ����B
�@�t�����X�̐��w�҃t�[���G�́A�u�M�̉�͓I���_�v�i�P�W�Q�Q�N�j�ɂ����āA��
�e(�w) ���t�[
���G�����ɓW�J�ł��邱�Ƃ��q�ׁA���̓��̔M�̓`�����͂��߁A���܂��܂Ȗ��̌�����
���p�����B
�@���������O�p�����̌����́A�P�W���I���̃_�j�G���E�x���k�[�C���n�܂�ł���B����
���̎O�p�����_�͗l�X�ȍ��������Ă����B�����̐��w�ҒB�́A���̗��_�̌�������
���g�B
�@�P�X���I�㔼�A�J���g�[�����W���_�̌������n�߂邫�������ƂȂ����̂��A���́A���̗�
�_�̌������Ɏ��g��ł̂��Ƃ炵���B
�@���ł́A�f�B���N���A���[�}���A���x�[�O��̌����ɂ��A���̗��_�͌���������A��͊w
����щ��p���ʂł͏d�v�Ȏ�@�ƂȂ��Ă���B
�@���āA�� �e(�w) �͘A���Ȃ̂ŁA�t�[���G�W���͑��݂��邪�A�ʂ����āA�t�[���G������
�� �e(�w) �Ɏ�������ł��낤���H
�@���̂��ƂɊւ��āA���̒藝���m���Ă���B
�藝�i�f�B���N���j
�@�@�� �e(�w) �͎��� �Q�� �������A�L�E�Ƃ���B�܂��A��� �m�|�� �C
�� �n ��K��
�@�ȗL���̋�Ԃɕ������A�e�X�Ŋ� �e(�w) �͒P���Ƃ���B
�@�@���̂Ƃ��A�t�[���G�����͎������A���̘a�́A�@�i1/2�j(�e(�w�{�O)�{�e(�w�|�O))
�@�@����ɁA�� �e(�w) �� �m�|�� �C �� �n �ŘA���Ȃ�A�t�[���G�����͈�l�������A
�@���̘a�́A �e(�w) �ɓ������B
�@����ʓI�ȗL�E�ϓ��Ȋ��ɑ��ẮA���̒藝�����藧�B
�藝�i�f�B���N���E�W�����_���j�@
�@�@�� �e(�w) �͎��� �Q�� �������A��� �m�|�� �C �� �n �ɂ����ē��������݂��A
�@�������������A���Ȃ�A�t�[���G�����͈�l�������A���̘a�́A �e(�w)
�ɓ���
�@���B
�@���悢��A���̃y�[�W�̖ڕW�ɑ��鏀�����������悤�ł���B
��@�āi�Q�j��(1/6)��2�@�ł��邱�Ƃ������B
�@�@�� �e(�w) �� �w2�@�i �|�� �� �w �� �� �j���A���� �Q�� �̎������Ƃ��ĉ�������B
�@���̂Ƃ��A
�@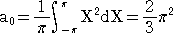
�ŁA����ɁA�����P�ɑ��āA�����P�� �� ��p���āA
�@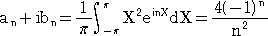
�����藧�B����āA
�@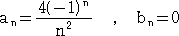
�ł���B
�i�� �e(�w) �͋���Ȃ̂ŁA���ʂȌv�Z�����Ȃ��Ă��A�������O�@�ł��邱�Ƃ͖��炩�B�j
�@���������āA�f�B���N���̒藝�ɂ��A
�@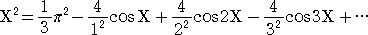
�����藧�̂ŁA�㎮�ɂ����āA�w�� �� ��������ƁA
�@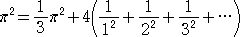
���������āA�āi�Q�j��(1/6)��2�@�����藧�B
�@�t�[���G������p����ƁA���낢��Ȗ��������̘a�����߂���B����́A�ǎ҂̂���
�̗��K���Ɏc���Ă������B
���K����@�@���̊��ɑ��ăt�[���G�������v�Z����ƁA�ǂ̂悤�Ȗ��������̘a����
�@�@�@�@�@�@�@�@�߂��邾�낤���H
�i�P�j�@�� �e(�w) �� | �w |�@�i �|�� �� �w �� �� �j �@�@�i�g������ �F
�w���O�@�Ƃ��Ă݂�B�j
| �i�Q�j |
�� |
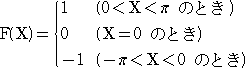 |
| �@�@�@�@�@�@�i�g������ �F �w����/�Q�@�Ƃ��Ă݂�B�j |
�i�Q�l�����F�����a��E����M�d�E�֓��@�B�@���@���_�@�P�@�i��g���X�j
�@�@�@�@�@�@�@��@�K�j�@���@������������@�i���q���X�j
�@�@�@�@�@�@�@�O���c�V���E��o�O�Y�@���@�����ϕ��w�@�i�w�p�}���o�ŎЁj
�@�@�@�@�@�@�@����@���@���@�����Ɛϕ��R�@�i��g���X�j�j
�i�NjL�j�@�����Q�P�N�U���P�S���t��
�@��L�̌v�Z�ŁA�I�C���[����S���ē������Ƃ��������@�āi�Q�j��(1/6)��2�@���t�[���G��
����p���Ĕ�r�I�ȒP�ɓ����ꂽ�B
�@�d�������� ����Ɍv�Z���Ă��炤�ƁA���������@�āi�Q�j���P�D�U�S�S�X�R�S�O�U�U�W�S�W�Q�R�E�E�E�@�ł���B
�@�����܂ŁA�ڂ����l��m��Ȃ��Ă��A�@�āi�Q�j���P�D�V�@���炢�͒m���Ă��đ��͂Ȃ����낤�B
�@���̂��Ƃ�b��ɂ�����肪�A�c��`�m��w�@���H�i�Q�O�O�S�j�ŏo�肳�ꂽ�B
�@
�Ƃ����Ƃ��A�S�Ă̎��R�� �� �ɑ��āA�@�r�����P�D�V�@�ł��邱�Ƃ����̂悤�ȍI���ȕ��@��
��莦�����B
�@���� �o �r���{�P/�� �p �͒P����������ł���B
�@���ۂɁA
�@�r��+1�{�P/(���{�P)�|�i�r���{�P/���j���P/�i���{�P�j2�{�P/(���{�P)�|�P/�����|�P/���i���{�P�j2���O
���A�m���ɁA���� �o �r���{�P/�� �p �͒P����������ł���B
�@����āA�@�r3�{�P/�R���P�D�U�X�S�S�E�E�E�@�ŁA�@�����R�@�̂Ƃ��A�@�r���{�P/�����r3�{�P/�R���P�D�V
�@�@�r�����r���{�P/�����P�D�V�@�Ȃ̂ŁA�@�����R�@�̂Ƃ��A�@�r�����P�D�V�@�����藧�B
�@�܂��A���� �o �r�� �p �͒P����������ł���A�@�r1���P�@�A�@�r2���P�{�P/�S���P�D�Q�T�@�ł���B
�@�ȏォ��A�S�Ă̎��R�� �� �ɑ��āA�@�r�����P�D�V�@�����藧�B
�i�R�����g�j�@���� �o �r�� �p �͒P����������ł���̂ɁA���� �o �r���{�P/�� �p ���P��������
�@�@�@�@�@�@��ɂȂ�͖̂��d�s�v�c�ȊW�ł��ˁI�����܂����D�D�D ��(^^;) �B
�i�NjL�j�@�����Q�S�N�U���P�W���t��
�@���g�o�����������b�ɂȂ��Ă���g�m�u�j�D�r�D�v����A�����Q�S�N�T���Q�W���t���Ŗ���
�����ɂ��Ă̘b������[���Œ������B
�@�u���a��������A�����̂S���܂ލ������ׂď����ē���ꂽ�����͎��������v
�@���P�^�ȉ��̐��̐����ŁA�����S���g��Ȃ����́A�S�ȊO�̂X�̐���������@����
���ׂĂO�̏ꍇ���������ɓ������̂ŁA �X���|�P����B
�@����āA�P�O������P�O���|�P�܂ł̐��̐����A���Ȃ킿�A���傤�ǂ��P�^�̐����ŁA�����S����
�܂Ȃ����̂̌��́A �X���|�P�|�i�X��-1�|�P�j���W�E�X��-1
�@�������̐��̋t���̘a���A �r���Ƃ���ƁA�������̐��ōŏ��̐��� �P�O��-1�ł��邩��A
�@�@�@�r�����P/�P�O��-1�{�E�E�E�{�P/�i�P�O���|�P�j���W�E�X��-1/�P�O��-1���W�i�X/�P�O�j��-1
���߂鋉���́A�@�r���r1�{�r2�{�E�E�E������=1�`�� �r��������=1�`�� �W�i�X/�P�O�j��-1���W�O
�@�L�E�ȁA�P����������́A��������̂ŁA
�@�u���a��������A�����̂O���܂ލ������ׂď����ē���ꂽ�����͎��������v
�@S(k)�F���������������̋Ɍ��l�̂Ƃ��A
�@�@S(1)��S(2) ��S(3) ��S(4) ��S(5) ��S(6) ��S(7) ��S(8) ��S(9) ��S(0)
�@����=1�`�� �P/��*���Q�R�D�P�O�R�S�T�E�E�E�@�i��*�F�O�̂Ȃ������j
�@�����P�O��40��ł��A�P�O�O���Ȃ����U�̒x���I�ł��B
�i�j�D�r�D����̃R�����g�j�@�����̖��ł��B�O�������������̘a�ȊO�ɂ��āA���̕�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���狳���Ē��������ł��B�������ƂĂ��ɖ��Ȃ̂ł悭�킩���
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@����B��낵�����肢���܂��B
�i�NjL�j�@�����Q�U�N�R���Q���t��
�@���g�o�����������b�ɂȂ��Ă���g�m�u�����v����̏o��ł��B
�@�����������炋�Ԗڂ̑f���� ��(��) �ƕ\�����Ƃɂ��܂��B���Ȃ킿�A
�@��(1)=2�C��(2)=3�C��(3)=5�C��(4)=7�C��(5)=11�C�c
�ł��B�f���̋t���a�����U���邱�ƁA�܂�A�������� ����=1�`�� �i�P/���i���j�j �����U���邱��
�͂悭�m���Ă��܂��B
�@�Ƃ��낪�A�f���Ԃ̑f���̋t���a ����=1�`�� �i�P/���i���i���j�j�j �͎������܂��B
���̂��Ƃ������Ă��������B
�@�f�`�h ���l�@����܂����B�i�����Q�U�N�R���Q���t���j
��=1�`���@�ɂ����āA
�@��=50000�@�̂Ƃ��A�@�a= 0�D9736563017379548544122950154
�@��=60000�@�̂Ƃ��A�@�a= 0�D9746369808742500396621039032
�@��=70000�@�̂Ƃ��A�@�a= 0�D9754435633464345929148976563
�@��=80000�@�̂Ƃ��A�@�a= 0�D9761260866161841036683906254
�@��=90000�@�̂Ƃ��A�@�a= 0�D9767159620433449411344267787
�@��=100000�@�̂Ƃ��A�@�a= 0�D9772345400112524763238719860
�@�@������������
�̂悤�ɕω����Ă����܂����B�i����ȏ��n�ł͎��̌v�Z�@�ł͔������Ȃ��Ȃ�܂����B�j
�@���܂Řa���Ƃ�Ƃ��Ă����U���Ă��܂����Ƃ͂Ȃ��ł��낤�Ƃ͑z���ł��܂����A�ؖ������
������ƁA�A�C�f�A���v�����܂���B
�@�����A��ʂɁA��(��(��)) �����ǂ�ω����A���̂悤�ɂȂ邱�Ƃ��ώ@���邱�Ƃ��牽�������
�肪���肪�Ƃ�Ȃ����̂�����D�D�D�B
p(p(1))=3�@�Ap(p(2))=5�@�Ap(p(3))=11�@�Ap(p(4))=17�@�Ap(p(5))=31�@�Ap(p(6))=41�@�Ap(p(7))=59
p(p(8))=67�@�Ap(p(9))=83�@�Ap(p(10))=109�@�Ap(p(11))=127�@�Ap(p(12))=157�@�Ap(p(13))=179
p(p(14))=191�@�Ap(p(15))=211�@�Ap(p(16))=241�@�Ap(p(17))=277�@�Ap(p(18))=283�@�Ap(p(19))=331
p(p(20))=353�@�Ap(p(21))=367�@�Ap(p(22))=401�@�Ap(p(23))=431�@�Ap(p(24))=461�@�Ap(p(25))=509
p(p(26))=547�@�Ap(p(27))=563�@�Ap(p(28))=587�@�Ap(p(29))=599�@�Ap(p(30))=617�@�Ap(p(31))=709
p(p(32))=739�@�Ap(p(33))=773�@�Ap(p(34))=797�@�Ap(p(35))=859�@�Ap(p(36))=877�@�Ap(p(37))=919
p(p(38))=967�@�Ap(p(39))=991�@�Ap(p(40))=1031�@�Ap(p(41))=1063�@�Ap(p(42))=1087
p(p(43))=1153�@�Ap(p(44))=1171�@�Ap(p(45))=1201�@�Ap(p(46))=1217�@�Ap(p(47))=1297
p(p(48))=1409�@�Ap(p(49))=1433�@�Ap(p(50))=1447�@�Ap(p(51))=1471�@�Ap(p(52))=1499
p(p(53))=1523�@�Ap(p(54))=1597�@�Ap(p(55))=1621�@�Ap(p(56))=1669�@�Ap(p(57))=1723
p(p(58))=1741�@�Ap(p(59))=1787�@�Ap(p(60))=1823�@�Ap(p(61))=1847�@�Ap(p(62))=1913
p(p(63))=2027�@�Ap(p(64))=2063�@�Ap(p(65))=2081�@�Ap(p(66))=2099�@�Ap(p(67))=2221
p(p(68))=2269�@�Ap(p(69))=2341�@�Ap(p(70))=2351�@�Ap(p(71))=2381�@�Ap(p(72))=2417
p(p(73))=2477�@�Ap(p(74))=2549�@�Ap(p(75))=2609�@�Ap(p(76))=2647�@�Ap(p(77))=2683
p(p(78))=2719�@�Ap(p(79))=2749�@�Ap(p(80))=2803�@�Ap(p(81))=2897�@�Ap(p(82))=2909
p(p(83))=3001�@�Ap(p(84))=3019�@�Ap(p(85))=3067�@�Ap(p(86))=3109�@�Ap(p(87))=3169
p(p(88))=3229�@�Ap(p(89))=3259�@�Ap(p(90))=3299�@�Ap(p(91))=3319�@�Ap(p(92))=3407
p(p(93))=3469�@�Ap(p(94))=3517�@�Ap(p(95))=3559�@�Ap(p(96))=3593�@�Ap(p(97))=3637
p(p(98))=3733�@�Ap(p(99))=3761�@�Ap(p(100))=3911�@�A�@������
�i���� ����̖��́A���݂܂�������Ă��܂���j
�@�f�`�h ����̃R�����g�ł��B�i�����Q�U�N�R���P�O���t���j
�@����=1�`�� �i�P/���i���j�j�@���v�Z�@�Ōv�Z�����Ă݂�ƁA
�@1/2+1/3+1/5+���+1/97=1.802817201048870939871615826
�@1/2+1/3+1/5+���+1/997=2.198080127175087541588476789
�@1/2+1/3+1/5+���+1/9973=2.483059947233560636099611335
�@1/2+1/3+1/5+���+1/99991=2.705272179047264148042556055
�@1/2+1/3+1/5+���+1/999983=2.887328099567672712348011299
�@�@�@�@�@��������������������������
�@1/2+1/3+1/5+���+1/1801241230056600467=3.99999999999999999966
�@1/2+1/3+1/5+���+1/1801241230056600523=4.00000000000000000021
�̋T�̕��݂̔@���̔����ɂ����Ȃ��B���ꂪ���U����Ƃ͂ɂ킩�ɂ͐M�����Ȃ��B�����
�ǂ��[�����邱�Ƃ��ł���̂ł��傤���H
�@�炷���邳��̃R�����g�ł��B�i�����Q�U�N�R���P�O���t���j
�@����=1�`�� �i�P/���j�@�����U���邱�Ƃ��M������̂ł���A�����悤�Ȃ��̂ł��B
�@����=1�`�� �i�P/���j�@���u100�v����̂́A
�@1/15092688622113788323693563264538101449859497
�܂ő��������ł��B
�i�NjL�j�@�u�x�������ւ̑Ή��v�Ƒ肵�āA�f�`�h����̂����e�ł��B�i�ߘa�Q�N�P�Q���Q�O���t���j
�@���X�l�������čs���Ȃ����Alim�������ł͔��U������Ă��鋉�� S(n)=��k=1n 1/k
�ŁA���̒l�����߂�10���z���Ă��܂����̒l�͉��ł��傤�H�܂��A100���鏉�߂Ă̂���
�@���قǂ��H
�@�炷���邳��̃R�����g�ł��B�i�ߘa�Q�N�P�Q���Q�O���t���j
�@��k=1n 1/k��10 �����ŏ��̂��́A12367
�@��k=1n 1/k��100 �����ŏ��̂��́A15092688622113788323693563264538101449859497
�ł��B���̒l�͏�L�ɂ�����܂��B�܂��A100�܂ł̓����́A�uA004080�v�ɂ���܂��B
�@�����Ɣ[�����₷�����������Ȃ�A����=1�`�� �P�@�͔��U���܂���ˁB
�@���̍ŏ���1���A 1/10000+1/10000+�c(10000��)�c+1/10000
����1���A 1/100000000+1/100000000+�c(100000000��)�c+1/100000000
����1���A 1/1000000000000+1/1000000000000+�c(1000000000000��)�c+1/1000000000000
�̂悤�ɕ�����ƁA�a�́A
1/10000+1/10000+�c(10000��)�c+1/10000
�@�@+1/100000000+1/100000000+�c(100000000��)�c+1/100000000
�@�@�@�@+1/1000000000000+1/1000000000000+�c(1000000000000��)�c+1/1000000000000
�@�@�@�@�@�@+�c
�̂悤�ɂȂ�܂����A�ŏ���1��1��1�����𑫂��Ă��������u3�v�ɂ����Ȃ�܂��A10100��
�𑫂��Ă��u25�v�ɂ��Ȃ�܂���B�ł��A���U���܂��B
�@�f�`�h ����̃R�����g�ł��B�i�����Q�U�N�R���P�P���t���j
�@���́u�ł��A�v�Ƃ������f�͌��̋������_���Ŕ��U����ƔF���ł��Ă��邱�ƂɋN�����Ă�
��̂ŁA�o���ς���ΎR�ƂȂ�̊��o�Ō����A
�@1+1/2+1/3+1/4+��������@���낤���A�@1+1/22+1/32+1/42+�������@���낤��
�����̍��̘a�Ƃ݂�A���U����Ɣ��f���Ă��܂��B�������A����́u���v�ɔ��U���A���
�́u��2/6�v�Ɏ�������B���̉��Ƃ��s�v�c�Ȋ��o���������ɂ͂��Ă܂��A���āu���U��
�����̋��ڂ͔@���Ȃ鐢�E���H�v�Ƃ����v�킳���B
�@�����ŁA����f���Ƃ��A�����������炋�Ԗڂ̑f���� ��(��) �ƕ\�����Ƃɂ��܂��B
p(1)=2�Cp(2)=3�Cp(3)=5�Cp(4)=7�Cp(5)=11�C�c
�ł��B
�f���̋t���a�����U���邱�ƁA�܂�A
�@�������� ��k=1�`�� (1/��(��)) �����U����B����A��k=1�`�� (1/(��(��)2)) �͎�������̂�
���U����̂��H�܂��A��k=1�`�� ((-1)k-1/��(��)) �͎����H�A���U�H
�̏ؖ����䑶�m�Ȃ狳���ĉ������B
�i�v�Z�Ŋm�F���邱�Ƃ��ł����A���O�ɔ��f���邱�Ƃ��ł��ʁB�_���Ŕ��f���邵���肪�Ȃ��B�j
���ǐL�@����t����ցA�����䑶�m�ł�����ȑO�f�ڂ���Ă���
�@�ł́A�������� ��k=1�`�� (1/��(��(��))) �ɂ��Ă͂ǂ��Ȃ̂ł��傤���H��k=1�`�� (1/��(��(��)))
�@���������邱�Ƃ������Ă��������B
�@����̏ؖ����@�������ĉ������B
�@���� ����̃R�����g�ł��B
�@�������� ��k=1�`�� (1/��(��(��))) ���������邱�Ƃ̏ؖ��́A�����Q�ƁB
�@�@�@�����ʐM�F�u�f����̍l�@�v�i�L���s������Z�@�˖쐣�@��Y�搶�j
�@�f�`�h ����̃R�����g�ł��B�i�����Q�U�N�R���P�P���t���j
�@�����Љ�Ă�������T�C�g���J���āA���C���悭�܂Ƃ߂�ꂽ�ؖ���ǂ�ł݂܂����B��
���ڂ����͌������Ă���܂��A�Ȃ�ƍ��Z���̑�\�I���W�`���[�g�̗����Ȃǂ�
�g�����Ȃ���A�܂�ʼnؗ�Ȃ�l�ߏ���������z���ł��B
�@���̖����Љ��Ă��炸���Ƃ�����v�Z���ڂ����Nj����Ă��A�����┭�U�̔��f��ۗ�
���Ȃ���Ȃ�Ȃ����ǂ������������Ȃ���A���Ƃ��q���g�͂Ȃ����̂��낤���Ɛ}���قɒʂ�
�Ă͊֘A�̏��Ђ���o�����ׂĂ����Ƃ���ł����B
�@���̏ؖ��̍Ō�̎Q�l�����ɍ���M�d���@�I�C���[�T���@�i�V���v�����K�[�W���p���j����
���Ă���A�܂������Q�`�R���O���炱�̖{��ǂݎn�߂�����ł����B
�@���̓v���̐��w�҂ł͂Ȃ��A�����܂ň��D�ƂƂ��Đ��w�̖ʔ����𖡂���Ă��闧��Ȃ̂�
�ǂ��t�������Ă�����ȏؖ����v�������Ƃ͂ł��܂��A�l�Ԃ̒������z������A������
�ő���p�����W��������͂͐��w�������Ė������������܂��B
�i�l����Ƃ��������̌��{����R�w�ׂ܂��B�j
�@���낢��Ȍ��ʂ����܂��g���킹�閭�Z�Ɋ������܂��B�i���ȑ��B���Ă����������̂悤�ł��B�j
�@���Ԃ������ďڍׂɗ��������Ă��������Ƃ������܂��B�Ԃ��Ԃ�����k=1�`��(1/(p(k))�͔��U
����̂ɁA��k=1�`��(1/p(p(k))) �͎�������Ƃ͕s�v�c�����ʔ����ł��ˁB������o�q�f����
�l�A���U�Ǝ����̐��ˍۂɂ����Ƒ��Â��������̗l�ł��B�������A�o�q�f�����L��������
�ł��邱�Ƃ��������Ă��Ȃ��̂ɁA�������邱�Ƃ��������Ă��邱�Ƃ�����ɓ��[�߂܂��B
�@�炷���邳��̃R�����g�ł��B�i�����Q�U�N�R���P�P���t���j
�@�����E���U�̋��ڂ́u�f���̋t���a�v�Ɓu�o�q�f���̋t���a�v�̊Ԃɂ���܂��B
�@�u ��k=1�`�� (1/(��(��)2)) �͎�������̂����U����̂��v�ɂ��ẮA�ȒP�ł��ˁB
1/��(��)2��1/��2�@����A0����k=1�`�� (1/(��(��)2))����k=1�`�� (1/��2)=��2/6�@�Ȃ̂Ŏ������܂��B
�@�u��k=1�`�� ((-1)k-1/��(��)) �͎����H�A���U�H�v�ɂ��ẮA S[n]=��k=1�`�� ((-1)k-1/��(��)) �Ƃ�
��ƁAS[2m]�́A0���傫���P�������AS[2m+1]�́A1/2 ��菬�����P�������ŁA
�@0��S[2m]��S[2m+1]��1/2�@���A�@limm���� �iS[2m+1]-S[2m]�j=limm���� 1/��(2m+1)
�Ȃ̂Ŏ������܂��B
�@�����l�́A�uA078437�v����u0.26960635197167�c�v�ł����A����ȍ~�̌��͂킩���Ă���
���݂����ł��ˁB
�@�j�r����̃R�����g�ł��B�i�����Q�U�N�R���P�Q���t���j
�@�f���̋t���̘a�͔��U����B�f���́A�Q�ƂR�ȊO�́A�U���{�P�^���U���|�P�^�ł��B������
�t���̘a�́A�ǂ�������U�������ł����A�ؖ�����Ă����ł��傤���H
�@���� ����̃R�����g�ł��B�i�����Q�U�N�R���P�Q���t���j
�@6n-1�^�̑f���̋t���a�͖�����ɔ��U���܂��B�܂��A6n+1�^�̑f���̋t���a���������
���U���܂��B
�@����Ɉ�ʂɁA���̂��Ƃ��ؖ�����Ă��܂��B
�@N��C�ӂ̐������Ƃ��Aa ��N�ȉ��̐������ł����āAN�ƌ݂��ɑf�ł���Ƃ��܂��B
���̂Ƃ��AN�Ŋ���Ɨ]�肪a�ɂȂ�悤�ȑf���̋t���̘a�͖�����ɔ��U���܂��B
�@�܂�A��p:�f���Cp��a(mod N) (1/p)�� ��
�@�f�`�h ���V���������N����܂����B�i�����Q�U�N�R���Q���t���j
�@������ρ@����=1�`�� �i���i���j2�{�P�j/�i���i���j2�|�P�j�@�͎�������B���̒l�����߂Ă��������B
�@���� ���l�@����܂����B�i�����Q�U�N�R���R���t���j
�@�^��=(��(2)/��(4))*��(2)=5/2
�i�NjL�j�@�ߘa�U�N�P�O���V���t��
�@���̓��k��w�@���n�i�P�X�W�Q�j�̖��́A������Ƃ������肵�Ղ���������Ȃ��B
���Q�@�@�����V�A�����Q�̓�������̈�ʍ��� ���� �Ƃ��A�����P/�R�A����P/�R�̓��䐔��
�@�@�̈�ʍ��� ��n �Ƃ���B����o�����p�ɂ��āA��k=1n ��k��k��k��(���{�P)(���{�Q)(���{�R)/�R
�@�@����������Ƃ��A���̖�ɓ�����B
�i�P�j�@��ʍ� ���� �����߂�B
�i�Q�j�@�������� ��n=1�� �P/���� �̘a�����߂�B
�i���j�i�P�j�@��ӂ��A�@�������V�{�Q�i���|�P�j���Q���{�T�@�A��n���i�P/�R�j�E�i�P/�R�jn-1���i�P/�R�jn
�����Q�@�̂Ƃ��A�@��������������(���{�P)(���{�Q)(���{�R)/�R�|��(���{�P)(���{�Q)/�R��(���{�P)(���{�Q)
�@���̂Ƃ��A�@�������Rn(���{�P)(���{�Q)/�i�Q���{�T�j�@�i�����Q�j
�����P�@�̂Ƃ��A�@�i�V/�R�j��1���W�@���A�@��1���Q�S/�V
�i�Q�j�@����=1�� �P/�������V/�Q�S�{����=2�� �i�Q���{�T�j/�o�R��(���{�P)(���{�Q)�p
�@���V/�Q�S�{����=2�� �m�P/�o�R��-1(���{�P)�p�|�P/�o�R��(���{�Q)�p�n
�@���V/�Q�S�{�P/�X�|�P/�o�R��(���{�Q)�p���V/�Q�S�{�P/�X�|�P/�o�R��(���{�Q)�p
�@���Q�X/�V�Q�|�P/�o�R��(���{�Q)�p
�@�� �� ���@�̂Ƃ��A�@�P/�o�R��(���{�Q)�p �� �O�@�Ȃ̂ŁA��n=1�� �P/���� ���Q�X/�V�Q�@�@�i�I�j
�@�@�ȉ��A�H�����I