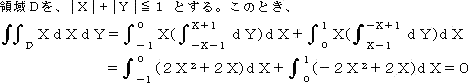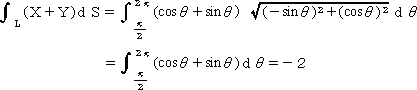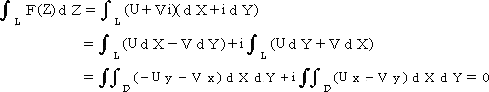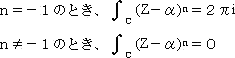表題の定理を紹介するために、いくつか言葉の定義をしなければならない。あまり厳密な定義
は、このホームページの性格上避けなければならないので、概略的な定義に留める。詳しくは、
専門書にあたられたい。
　ａ、ｂを実数として、「ａ＋ｂｉ」の形の数を複素数という。ここで、i は２乗すると−1になる性質を
持つ。複素数と平面上の点は１対１に対応する。従って、複素数全体というのは、平面全体をイ
メージしてもらえばよい。
　連結な開集合を領域という。これも、切れ目のない漠然とした広がりと考えればよろしい。
領域Ｄの各点Ｚに、それぞれ１つの複素数Ｗが対応しているとき、ＷはＺの関数であるという。
領域Ｄのある点で、関数が微分可能ということも、実数関数のときの微分可能の定義を拡張し
たものと考えてよろしい。領域Ｄの各点で微分可能であるとき、関数は正則であるという。
　（この「正則」という言葉は、コーシーが１８２０年代より使い始めたらしい）

定理Ａ　　関数Ｆ(Z)が領域Ｄで正則ならば、コーシー・リーマンの関係式が成り立つ。
　　　すなわち、Ｆ(Z)＝U＋Ｖi　、Ｚ＝Ｘ＋Ｙi　のとき、　Uｘ＝Ｖｙ　、Uｙ＝−Ｖｘ
　　　　　　　　　　　　　　　　　　　　　　　　　　　（ここで、UｘはUのＸに関する偏微分で、他も同様）
　　　逆も成立する。
（証明）　Ｗ＝Ｆ(Z)＝U＋Ｖi　とおくと、Ｚｘ＝１、Ｚｙ＝i　であることに注意して
　　　　　Ｗｘ＝Uｘ＋i Vx＝Ｆ’(Z)Ｚｘ＝Ｆ’（Ｚ）　　　　（但し、Ｆ’はＦの微分である。他も同様）
　　　　　Ｗｙ＝Uｙ＋i Ｖｙ＝Ｆ’(Z)Ｚｙ＝Ｆ’(Z)i
　　よって、Uｘ＋i Vx＝−i （Uｙ＋i Ｖｙ）＝Ｖｙ−i Uy
　　従って、Uｘ＝Ｖｙ　、Uｙ＝−Ｖｘ　が成り立つ。
逆の証明は略する。（全微分の定義を用いることにより示される）

コーシー・リーマンの関係式が成り立たないと、関数は正則とはならないので、これはかなり厳
しい条件である。

(例）　正則でない関数と正則な関数

　関数 Ｆ(Ｚ)＝Ｘ²＋ｉＹ²　は正則でない。関数 Ｆ(Ｚ)＝Ｘ²−Ｙ²＋２ｉＸＹ　は正則。

　１変数の関数の定積分は、図形の面積を１つのモデルとしている。２変数の関数の定積分
は、空間の曲面とＸＹ平面との間に生ずる体積をモデルとしている。

　関数Ｆ（Ｘ、Ｙ）の有界閉領域Ｄにおける定積分は、

　　　　　　　

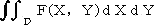
　と表される。この積分は、逐次積分により求められる。

(例）逐次積分

　

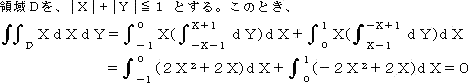
　平面内にＡを始点、Ｂを終点とする１つの曲線Ｌを考え、Ｌに沿った積分

　　　　　　　

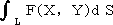
を線積分という。

（例）線積分
　平面上、点（０，１）から原点中心、半径１の円周上を半時計回りに進み、点（１，０）に至
る曲線をＬとする。このとき、

　　　　　

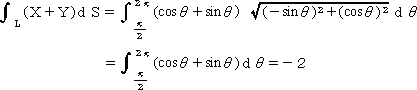Ｇｒｅｅｎの定理　　閉領域Ｄの周を正の向き（領域Ｄ内の点を左手にみるように半時計回
　　　　　　　　　　　りに進む）にとって、Ｌとするとき、

　　　　　　　　　　

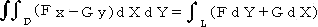
証明は略するが、逐次積分の考えにより、計算される。
　この定理は、重積分と線積分との関係を表すもので、左辺のＤ上での積分値が、実はＬ
上でとる値だけで定まってしまうということを表している。

コーシーの積分定理　　関数Ｆ（Z)が閉曲線ＣおよびＣで囲まれた領域Ｄ上で正則ならば、

　　　　　　　　　　　　　　　　　　　　　

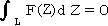
(証明）　まず、Ｆ(Z)＝U＋Ｖi が正則なので、Uｘ＝Ｖｙ　、Uｙ＝−Ｖｘ　が成り立つ。
　　　　このとき、Ｇｒｅｅｎの定理により、

　　　　　

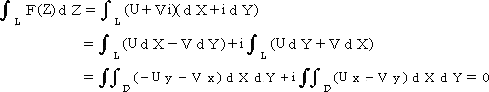
次の定理はコーシーの積分定理より帰結される。

定理Ｂ　　ＬとＬ’は単一閉曲線（始点と終点が一致し、それ以外一致しない）で正の向き
　　　　にまわる向きをもつ。Ｌ’はＬに囲まれた閉領域に含まれ、ＬとＬ’に囲まれた領域上
　　　　で、関数Ｆ（Z)が正則ならば、

　　　　　　　　　

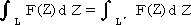
この定理は、次のように一般化される。

定理Ｃ　　Ｌは点α、β、・・・、γを内部に含む単一閉曲線で、ＬおよびＬで囲まれた領域
　　　　上で、関数Ｆ（Z)は正則とする。また、点α、β、・・・、γを中心とし、Ｌの内部に円
　　　　周Ａ、Ｂ、・・・、Ｃをかくとき、次が成り立つ。

　　　　　　　　

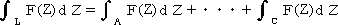定理Ｄ（ある特殊な定積分の計算）　Ｃを中心α、半径ｒの円周とする。このとき、

　　　　　　　　

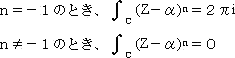
（証明）　　Ｚ−α＝ｒ・ｅ^ｉθ　と置換することにより直ちに求められる。

留数（Residue）　　関数Ｆ(Z)がαで正則でないが、αのある近傍ではα以外の全ての
　　　　点で正則なとき、αを関数Ｆ(Z)の孤立特異点という。このとき、

　　　　　　　　　　　

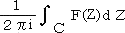
　　　　の値は曲線Ｃの選び方に無関係に定まる。この値を、関数Ｆ(Z)のαにおける留数
　　　　といい、Res（α）と表される。

留数の計算　　次の２つの方法が簡便である。ほかに、部分分数分解による方法もある。

（方法その１）　αがＦ(Z)の孤立特異点で、Ｚ→αのときの（Ｚ−α）Ｆ(Z)の極限値Ｒが存
　　　　　　　　在するとき、Ｒes（α）＝Ｒ　である。

（方法その２）　Ｆ(Z)、Ｇ(Z)がαで正則で、Ｇ(α)＝０、Ｇ’(α）≠０のとき、
　　　　　　　　Ｆ/G　の留数 Ｒes（α）は、Ｆ(α)／Ｇ’(α)　に等しい。

（例）　Ｆ(Z)＝１／Ｚ（Ｚ−２i）において、α＝０、２i
　　　このとき、Ｒes（０）＝i／２、　Ｒes（２i）＝−i／２　である。

留数定理　　関数Ｆ（Z)が閉曲線Ｃ内に孤立特異点α１、α２、・・・、αｎ を持ち、それ以
　　　　　　　外の閉曲線ＣおよびＣで囲まれた領域Ｄ上で正則であるとする。このとき、

　　　　　　　　　　　　　

　　証明は、留数の定義と定理Ｃから明らかであろう。

（例）留数定理を用いた定積分の計算

　　

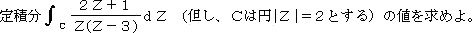
　　（解）　Ｒes（０）＝−１／３ なので、求める値は、−２πi／３ である。

　余談になるが、留数定理を大学２年生のときに学んで、大いにショックを受けたことを覚
えている。なぜなら、積分の計算なのに、そういう計算もなく、積分が求まってしまうから。
「ちょっとズルだな〜？」というのが、その当時受けた印象である。（塾長）