ここでは、１．で解いた例題を、留数定理を用いて解いてみよう。
このように、本来は実数関数の定積分の問題なのだが、複素数関数の定積分の問題に
翻訳すると、実に見通しよく、どんな定積分の問題も統一的に解くことができる。
これが、コーシーの目指したものなのだろう。このようなエレガントな解答は、私にとっても
非常に魅力的である。解析の中に複素数を取り入れようとする試みは、実はコーシーよりも
１００年以上前の１７０２年ジャン・ベルヌーイによってなされている。
数学以外にも、電気関係とか、複素数のお世話になっている学問は数多い。読者の方は、
この先の物語を、是非自分の手と足を使って、踏破してもらいたい。
当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんからの出題です。
（平成２３年９月１６日付け）
を特別講義「留数定理の応用」のページを参考に解いているのですが、実数の範囲だと、
tan(θ/2)=t と置いて・・・ とやっても、cosθもsinθもあるからお手上げ・・・。ちなみに、
答えはπ(半径1の円の面積と同じ)です。
当ＨＰがいつもお世話になっているＨＮ「ＦＮ」さんに回答していただきました。
（平成２３年９月１７日付け）
「留数定理の応用」のページと同じようにやればできると思います。平方完成が必要です。
（解） tan(θ/2)=t と置くと、 cosθ= (1-ｔ2)/(1+ｔ2) 、sinθ= 2ｔ/(1+ｔ2) なので、
3-2cosθ＋sinθ= (5ｔ2+2ｔ+1)/(1+ｔ2)
また、 (1/2cos2(θ/2))ｄθ＝ｄｔ より、 ｄθ＝ 2cos2(θ/2)ｄｔ＝2ｄｔ/(1+ｔ2)
これらを代入して、
(1/(3-2cosθ＋sinθ))dθ= (2/(5ｔ2+2ｔ+1))dt
5ｔ2+2ｔ+1=5{(t+1/5)2+(2/5)2} において、t+1/5=(2/5)tanφ とおくと、
(t+1/5)2+(2/5)2=(2/5)2/cos2φ
dt = (2/5)/(cos2φ)dφ だから、 (2/(5ｔ2+2ｔ+1))dt = 2/5・(5/2)2・(2/5)dφ = dφ
積分区間は、θが、0〜2π 、t が、0〜∞ と -∞〜0 即ち、-∞〜∞ で、
t+1/5も、-∞〜∞ よって、φは、-π/2〜π/2
以上から、
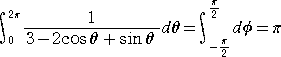（終）
-2cosθ＋sinθを合成して、
sin(θ+α)として、θ+αをあらためてθとおけば、積分区
間は、αからα+2πになるけど、周期２πの周期関数なので、0 から 2π でよい。
与式=∫[0→2π](1/(3＋√5sinθ))dθとなるので、これを計算してもよい。
合成は、ｓｉｎ より ｃｏｓ の方がいいようです。平方完成の必要がないから。３とという係
数は、ａ と ｂ にしてもあまり差がないです。むしろ、ａ と ｂ の方がやりやすいかもしれません。
ただし、ａ＞ｂ＞0 は必要です。
∫[0→2π](1/(a＋bcosθ))dθを計算する。途中で、ａ2-ｂ2 を ｃ2(ｃ＞0)と置いた方がよい。
答えは、2π/ｃ となるはず。
（コメント） よおすけさんの問題を留数定理を用いて解いてみた。
において、 ｚ＝ｅｉθ とおくと、 ｄｚ＝ｉｚｄθ で、
ｃｏｓθ＝（ｚ＋１/ｚ）/２ 、 ｓｉｎθ＝（ｚ−１/ｚ）/２ｉ
このとき、 ３−２ｃｏｓθ＋ｓｉｎθ＝｛（−２−ｉ）ｚ2＋６ｚ−２＋ｉ｝/２ｚ なので、
を計算すればよい。
（１−２ｉ）ｚ2＋６ｉｚ−１−２ｉ＝０ の解は、ｚ＝（２−ｉ）/５ 、２−ｉ で、ｚ＝（２−ｉ）/５ が、領
域 ｜ｚ｜≦１ に含まれる唯一の孤立特異点である。
このとき、簡単な計算から、 Ｒｅｓ（（２−ｉ）/５）＝−ｉ/２ であるので、求める積分値は、
与式＝２πｉ×（−ｉ/２）＝π
となる。
よおすけさんからのコメントです。（平成２４年１１月７日付け）
上記で、∫[0,π/2]{1/(5+3cos4x)}dx という定積分が紹介されています。この式で、4x=θと
置き換えた定積分が、(1/4)∫[0,2π]{1/(5+3cosθ)}dθとなっていますが、積分される式が
1/(5+3cosθ)でなく、1/(5+3sinθ)だったら計算結果はどうなるのでしょう？
途中計算は異なりますが、実は、同じ 1/4×π/2=π/8 という結果になります。それぞれ
違う値になると最初思っていましたので、びっくりしています。管理人さんの解法に倣って書
けば、
∫[0,2π]{1/(5+3sinθ)}dθで、z=e^iθとおくと、dz=izdθ、sinθ=1/2i(z-1/z)より
∫[0,2π]{1/(5+3sinθ)}dθ=∫|z|=1{2/(3z^2+10i-3)}dz・・・★
★で、3z^2+10i-3=0としてzについて解くと、z=-i/3、-3i。
|z|≦1から、z=-i/3 のみが領域|z|≦1に含まれる唯一の孤立特異点。
このとき、Res(-i/3)={2/(8i)}=1/4i より、 ★=2πi×1/4i=π/2
以上から、与式=1/4×π/2=π/8
（※Resのところは自信なかったですが、とりあえず挙げました。）
らすかるさんからのコメントです。（平成２４年１１月８日付け）
sinθは周期2πで、その１周期全体に対する積分ですから、位相を90°ずらしてcosθにし
ても同じ値になりますね。式で書くと、
∫[0〜2π]{1/(5+3sinθ)}dθ=∫[π/2〜5π/2]{1/(5+3sinθ)}dθ
=∫[π/2〜5π/2]{1/(5+3cos(θ-π/2))}dθ
=∫[0〜2π]{1/(5+3cosφ)}dφ （φ=θ-π/2とした）
よおすけさんからのコメントです。（平成２４年１１月８日付け）
sinθの周期が2πとは気づきませんでした。ご回答ありがとうございます。