幾何の問題２

幾何の問題２　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんからの出題です。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２４年５月５日付け）

　半径ｒｃｍの円の直径の上に、大きさの違う２つの円が並んでいます。

　この２つの円の直径が16cm、18cm のとき、ｒを求めなさい。

（答）　空舟さんから解答をお寄せいただきました。（平成２４年５月７日付け）

　円A、B、Cがあって、それぞれ半径9、8、r であって、円A、Bは互いに外接しつつ、共に
円C及び円Cの直径Lに接しているという図で解釈しました。

　　　　　　

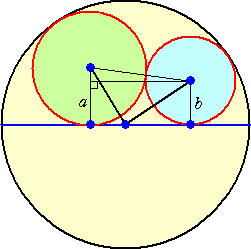
　方程式は、三平方の定理を用いて

　　√[(r-a)²-a²] + √[(r-b)²-b²]＝√[(a+b)²-(a-b)²]

　これより、　r = ｛-2ab(a+b)±4ab√(2ab)｝/(a²-6ab+b²)

a=9、b=8　として正の数ｒを求めると、　r=144/7　を得ます。

　よおすけさんからのコメントです。（平成２４年５月７日付け）

　空舟さん、ありがとうございます。すいません。問題文変えます。

　半径12cmの大きい円の直径の上に同じ大きさの小さい円が３個並んでいます。小さい円
３個は、互いに外側で接しており、大きい円とは内側で接しています。
　小さい円の半径は何cmですか。

当初は小学3・4年生向けに作ったつもりですが、いざ作るってなると奇妙なものになります。

（コメント）　完成図がイメージできない．．．？

　空舟さんからのコメントです。（平成２４年５月１０日付け）

　上記の２題目について、「直径の上に並んでいる」という表現がどうも曖昧に感じますが、
小円A、B、Cと大円Oがあって、AとCが直径Lに接していると解釈しました。
（A、B、Cはこの順に外接し合い、大円に内接している）

　対称性の考察から、OとCの中心を結ぶ線分は直径Lと30度で交わるので、その線分の
長さは小円の半径の2倍であり、従って、大円の半径：小円の半径＝３：１であることがわ
かります。

　中年Ａさんからのコメントです。（平成２４年５月１７日付け）

　上記の話題に触発されて投稿します。よおすけさんは問題を修正されてますが、小生が
考えていますのは修正前の問題です。

　半径ｒｃｍの円の直径の上に、大きさの違う２つの円が並んでいます。
この２つの円の直径が16cm、18cm のとき、ｒを求めなさい。

　この問題について、空舟さんは、

　円A、B、Cがあって、それぞれ半径9、8、r であって、円A、Bは互いに外接しつつ、
共に円C及び円Cの直径Lに接している

という図で解釈されたとのことです。

　小生は、この問題の構図の背景は何かと問題を設定し、次のことに至りました。

　円Ｃと円Ａ、Ｂの接点をＰ、Ｑとする。円Ｃの直径と円Ａ、Ｂの接点をＲ、Ｓとする。このとき、

ＰＲ、ＱＳ、円Ｃは一点で交わる。換言すると、ＰＲ、ＱＳを円の内部で延長すると、円Ｃの円

周上の点Ｔで交わる。

　　　　　

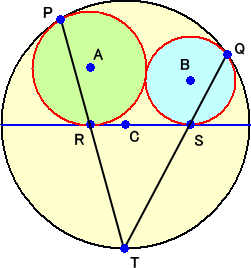
　ここから円Ｃの直径を求めることは出来ないかと考えています。

　さらに、この構図を眺めながら小生が以前に投稿の「東北大学の２０１２年入試問題」を想
起しました。本サイト「初等幾何？」にまとめられている内容です。関連の有無は？と考えて
います。試行錯誤を継続しようと想念しています。

（コメント）　上記事実の証明を考えてみました。

　直線ＰＲ、直線ＱＳが円Ｃと交わる点をそれぞれＸ、Ｙとおくと、

　∠ＡＲＰ＝∠ＡＰＲ＝∠ＣＰＲ＝∠ＣＸＲ　より、ＡＲとＣＸは平行になる。

　ＡＲは直径に対する垂線なので、ＣＸも直径に対する垂線となる。

　　同様にして、

　∠ＢＳＱ＝∠ＢＱＳ＝∠ＣＱＳ＝∠ＣＹＳ　より、ＢＳとＣＹは平行になる。

　ＢＳは直径に対する垂線なので、ＣＹも直径に対する垂線となる。

　　以上から、Ｘ＝Ｙ＝Ｔ　となる。

　よおすけさんからのコメントです。（平成２４年５月１７日付け）

　僕の場合は単に、「お茶の間」だからできるだけ簡単なものを出題しよう・・・ただそれだけ
でした。投稿「初等幾何？」を意識してはいません。参考にしたのが、僕が小学3年の時に使
っていた教科書です。円と球という単元があり、その練習問題を参考にしたのですが、ここは
文字掲示板なので絵が描けず、投稿するまで、文だけでどう説明しようか・・・となり、あの文
章題にしましたが、こちらも苦い思いをすることに・・・。

　攻略法さんからのコメントです。（平成２４年５月１９日付け）

　「初等幾何？」の円周角∠BPＱ＝π/４として、点P、Qを考える。このとき、点P、Qは「幾
何の問題２」の半円に内接する円の接点P、Rとなる。「周上の点Ｔで交わる。」の証明の図
の場合、半円の直径の右端をXとすると、

　　　円周角∠XPR＝∠XPT＝π/４　、中心角∠XCT＝π/２

である。

　空舟さんからのコメントです。（平成２４年５月２０日付け）

　今回の結果から検証すると、

　点T、線分RSの中点、円A、Bの外接点の３点は同一直線上にある
　（その直線は円A,Bの共通接線）

と成り立っていましたが、根拠は分かっていません。とりあえず指摘してみました。参考にな
れば幸いです。

　空舟さんからのコメントです。（平成２４年５月２２日付け）

　（上記証明の補足）

　底角が等しい二等辺三角形は相似（△PAR∽△PCT）です。そうすると、RがAの真下にあ
るので、TもCの真下にあるはずと理解されます。

　点T、線分RSの中点、円A、Bの外接点の３点は同一直線上にある

について、P、Q、R、Sは同一円周上にあることが示せます。

　PQと円A、Bの交点を p、q とすれば、□PRAp∽□QSBq より、∠RPQ＝∠SP'Q＝∠RST

　それを使って、円A、Bの共通接線がTを通ることが示せます。

　点Tから円A、Bに引いた接線の長さは、それぞれ √（TS・TQ）と√（TR・TP）で一致する。
（方べきの定理）