丂悢乯偺旝愊暘偲偄偆栤戣偵側傠偆偐偲峫偊傞偺偱偡偑丄
丂愝掕偐傜峫偊傞偲丄乽弶摍婔壗乿偱傾僾儘乕僠偱偒傞偺
丂偱偼側偄偐偲巚偭偰偄傑偡丅
丂丂丂搶嫗戝妛慜婜棟宯乮2012乯偺戞1栤偵傕嫟捠偡傞
丂丂媈栤側偺偱偡偑丏丏丏丅
丂丂乽弶摍婔壗偵峉傞昁梫偑偁傞偐丠乿偲栤傢傟傑偟偨
丂側傜廫暘側夝偼梡堄偱偒偰偄側偄偺偱偡偑丄乽弶摍婔
丂壗偼柺敀偄乿偲偄偆慺杙側巚偄偐傜丄偙偆偟偨偙偲傪峫
丂偊偨偄偲丏丏丏丅
丂奆偝傑丄偛専摙偔偩偝偄傑偡偲婐偟偒偙偲偱偡丅
丒弶摍婔壗丠丂丂丂丂丂 丂丂 丂丂 丂丂丂 丂丂丂 丂丂丂拞擭俙 巵
丂搶杒戝妛慜婜棟宯乮俀侽侾俀擭乯丂戞俆栤偵壓婰偑弌戣偝傟傑偟偨丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮暯惉俀係擭俁寧侾侽擔晅偗乯
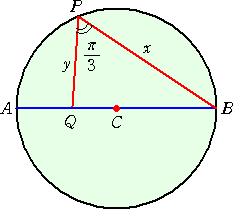
丂挿偝侾偺慄暘俙俛傪捈宎偲偡傞墌廃俠忋偵揰俹傪偲傞丅偨偩偟丄揰俹偼揰俙丄俛偲偼堦抳
偟偰偄側偄偲偡傞丅慄暘俙俛忋偺揰俻傪佢俛俹俻亖兾/俁偲側傞傛偆偵偲傝丄慄暘俛俹偺挿偝
傪 倶 偲偟丄慄暘俹俻偺挿偝傪 倷 偲偡傞丅埲壓偺栤偄偵摎偊傛丅
丂乮侾乯丂倷 傪 倶 傪梡偄偰昞偣丅
丂乮俀乯丂揰俹偑俀揰俙丄俛傪彍偄偨墌廃俠忋傪摦偔偲偒丄倷 偑嵟戝偲側傞 倶
傪媮傔傛丅
 |
丂丂忋婰偺栤戣偼丄婎杮揑偵偼丄暘悢娭悢乮or 嶰妏娭 丂悢乯偺旝愊暘偲偄偆栤戣偵側傠偆偐偲峫偊傞偺偱偡偑丄 丂愝掕偐傜峫偊傞偲丄乽弶摍婔壗乿偱傾僾儘乕僠偱偒傞偺 丂偱偼側偄偐偲巚偭偰偄傑偡丅 丂丂丂搶嫗戝妛慜婜棟宯乮2012乯偺戞1栤偵傕嫟捠偡傞 丂丂媈栤側偺偱偡偑丏丏丏丅 丂丂乽弶摍婔壗偵峉傞昁梫偑偁傞偐丠乿偲栤傢傟傑偟偨 丂側傜廫暘側夝偼梡堄偱偒偰偄側偄偺偱偡偑丄乽弶摍婔 丂壗偼柺敀偄乿偲偄偆慺杙側巚偄偐傜丄偙偆偟偨偙偲傪峫 丂偊偨偄偲丏丏丏丅 丂奆偝傑丄偛専摙偔偩偝偄傑偡偲婐偟偒偙偲偱偡丅 |
乮嶲峫乯丂搶嫗戝妛慜婜棟宯乮2012乯丂戞1栤
丂丂丂丂丂師偺楢棫晄摍幃偱掕傑傞嵗昗暯柺忋偺椞堟俢傪峫偊傞丅
丂丂丂丂丂丂丂倶2亄乮倷亅侾乯2亝侾丂丄丂倶亞![]() /俁
/俁
丂丂丂丂捈慄 倢 偼尨揰傪捠傝丄俢偲偺嫟捠晹暘偑慄暘偲側傞傕偺偲偡傞丅偦偺慄暘偺挿偝俴偺
丂丂丂丂嵟戝抣傪媮傔傛丅傑偨丄俴偑嵟戝抣傪偲傞偲偒丄倶 幉偲 倢 偺側偡妏兤乮侽亙兤亙兾/俀乯
丂丂丂丂偺梋尫 們倧倱兤 傪媮傔傛丅乮摎偊丗丂俴偺嵟戝抣偼丄![]() /俁丂丄們倧倱兤亖侾/
/俁丂丄們倧倱兤亖侾/![]()
乮僐儊儞僩乯丂乽弶摍婔壗乿偱偼側偄丄偡偖巚偄偮偔夝朄傪傑偢妋擣偟偰偍偒偨偄偲巚偄傑偡丅
乮侾乯丂佢俙俛俹亖兤乮侽亙兤亙兾/俀乯偲偍偔偲丄丂倶亖們倧倱兤
丂佢俹俻俛亖俀兾/俁亅兤丂側偺偱丄惓尫掕棟傛傝丄
丂丂倷/倱倝値兤亖倶/倱倝値乮俀兾/俁亅兤乯丂側偺偱丄丂倷亖倱倝値兤們倧倱兤/倱倝値乮俀兾/俁亅兤乯
丂傛偭偰丄壛朄掕棟傛傝丄
丂丂倷亖倱倝値兤們倧倱兤/乷乮![]() /俀乯們倧倱兤亄乮侾/俀乯倱倝値兤乸
/俀乯們倧倱兤亄乮侾/俀乯倱倝値兤乸
丂丂亖俀倱倝値兤們倧倱兤/乮倱倝値兤亄![]() 們倧倱兤乯
們倧倱兤乯
丂侽亙兤亙兾/俀丂側偺偱丄丂倱倝値兤亖併乮侾亅倶2乯
丂埲忋偐傜丄丂倷亖俀倶併乮侾亅倶2乯/乷併乮侾亅倶2乯亄![]() 倶乸
倶乸
乮俀乯丂倷亖俀倱倝値兤們倧倱兤/乮倱倝値兤亄![]() 們倧倱兤乯丂傛傝丄
們倧倱兤乯丂傛傝丄
丂丂丂倄亖侾/倷亖乮![]() /倱倝値兤亄侾/們倧倱兤乯/俀丂偲偟偰丄
/倱倝値兤亄侾/們倧倱兤乯/俀丂偲偟偰丄
丂丂丂倓倄/倓兤亖乮亅![]() 們倧倱兤/倱倝値2兤亄倱倝値兤/們倧倱2兤乯/俀
們倧倱兤/倱倝値2兤亄倱倝値兤/們倧倱2兤乯/俀
丂丂丂丂丂丂丂丂亖乮倱倝値3兤亅![]() 們倧倱3兤乯/乮俀倱倝値2兤們倧倱2兤乯
們倧倱3兤乯/乮俀倱倝値2兤們倧倱2兤乯
丂丂丂倓倄/倓兤亖侽丂偡側傢偪丂倱倝値3兤亅![]() 們倧倱3兤亖侽丂傛傝丄丂倲倎値3兤亖
們倧倱3兤亖侽丂傛傝丄丂倲倎値3兤亖![]() 丂偲側傞兤偼
丂偲側傞兤偼
丂丂侾屄懚嵼偟偰丄偦偺抣傪兛偲偡傞偲丄倄偼丄兤亖兛偱嬌彫偐偮嵟彫偲側傞丅
丂丂偡側傢偪丄丂倷 偼丄兤亖兛偱嬌戝偐偮嵟戝偲側傞丅
丂丂丂偟偨偑偭偰丄丂倶亖們倧倱兤亖侾/併乮侾亄俁1/3乯
乮仸丂摎偑悘暘墭偄偱偡偹両杮斣偱偙傫側悢帤傪摫偄偨傜丄帺怣偑帩偰傑偣傫丏丏丏倖(^^;)乯
丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俁寧侾侾擔晅偗乯
丂偝偡偑偵婔壗揑偵偼尩偟偄偲巚偭偨偺偱偡偑丄側傫偲偐偦傟偭傐偄姶偠偵偼偱偒傑偟偨丅婔
壗揑側旝暘傪峫偊傞曽朄偱夝偒傑偟偨丅
丂丒乽Q偲墌偺拞怱偺嫍棧 亖 P偐傜AB偵堷偄偨悅慄偺懌偲墌偺拞怱偺嫍棧乿偲偄偆拞娫寢壥
丂傪摼傑偡丅偦偺屻偼4師曽掱幃偑弌偰偒傑偡丅
乮夝乯丂PQ偺墑挿偲墌偺岎揰偼掕揰偱偁傞丅偙傟傪Z偲偍偔丅墌廃妏偺掕棟傛傝丄屖倅B偼墌廃
丂偺俁暘偺侾偱偁傞丅捈慄ZQP偲AQB偲偺側偡妏傪倯丄捈慄ZQP偲P偱偺墌偺愙慄偺側偡妏傪
丂倫偲偍偔丅乮側偡妏偼揔摉偵偦傟偭傐偄曽丅乯
丂慄暘ZQ傪丄d兤妏搙偩偗摦偐偟偨帪偺ZQ丄ZP偺婔壗揑側旝暘傪峫偊傞丅
乮恾傪昤偄偰ZQ偑旝彫曄壔偟偨帪偺ZQ丄ZP偺挿偝曄壔傪峫偊傞丅仸晞崋偑柺搢側偺偱丄愨懳抣傪偮偗傑偟偨両乯
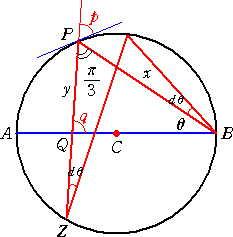 丂丂丂嵍恾偵偍偄偰丄
丂丂丂嵍恾偵偍偄偰丄
丂丂丂丂|d(ZQ)|亖ZQ丒d兤/|tan(倯)|丂丄
丂丂丂丂|d(ZP)|亖ZP丒d兤/|tan(倫)|
丂丂偲側傝傑偡丅慄暘PQ偑嬌抣傪庢傞帪丄偙傟傜偼堦抳
丂丂偡傞両偡側傢偪丄
丂丂丂丂ZQ / |tan(倯)| 亖ZP / |tan(倫)|
丂偑惉傝棫偮丅
丒揰P傪捠傞AB偵暯峴側捈慄傪堷偒墌偲偺傕偆1偮偺岎揰傪P乫偲偍偔丅
乮PQ偑嵟戝偺帪偱偼丄恾偐傜偟偰丄P乫偼P傛傝傕A懁偵偁傞偼偢丏丏丏丅乯
丂愙尫掕棟偐傜佢ZP乫P亖兾亅倫丂偱偁傝丄暯峴慄偺摨埵妏偱佢ZPP乫亖倯丂偱偁傞丅
丂仮ZPP乫偱惓尫掕棟傪揔梡偟偰丄忋幃傪惍棟偡傞偲埲壓傪摼傞偙偲偑偱偒傞丅
丂丂ZQ丒 |cos(倯)|= ZP乫丒 |cos(倫)|
丂偡側傢偪丄P乫偐傜AB偵堷偄偨悅慄偺懌偼丄Q偵堦抳偡傞丅
丒Q偲墌偺拞怱偺嫍棧傪 倱 偲偍偔丅P乫偺掕媊傛傝戜宍PP乫AB偼懳徧偩偐傜丄P偐傜AB偵堷偄
偨悅慄偺懌偲墌偺拞怱偺嫍棧傕s偲側傞丅偁偲偼丄Z偺埵抲偲敿宎亖1/2偲嶰暯曽偺掕棟傪嬱
巊偡傟偽椙偄丅
丂ZQ 丗 QP 亖 ![]() /4 丗 併(1/4-倱2)
/4 丗 併(1/4-倱2)
丂偙傟偼丄AB偵堷偄偨ZQ丄QP偺塭偺斾丂1/4-倱 丗 2倱丂偲堦抳偡傞丅
丂傛偭偰丄曽掱幃丂3倱2/4亖(1/4-倱2)(1/4-倱)2丂傪摼傞丅
丂惍棟偟偰場悢暘夝偡傞偲丄丂(4倱+1)(16倱3-12倱2+12倱-1)=0丂偱丄
丂丂8倱3+12倱2+6倱+1亖3(-8倱3+12倱2-6倱+1)丂偐傜丄(1+2倱)3亖3(1-2倱)3
偲曄宍偝傟傞傛偆偱偡丅帺暘偱偙偆曄宍偡傞偺偼擄偟偄偱偡偑...丅偲傕偐偔丄3師偺曽偺幚悢夝
偼僐儞僺儏乕僞偵傛傟偽丄丂倱=(-32/3+31/3+1) /4
丂偁偲偼丄嶰暯曽偺掕棟偱丄倶丄倷 傪摼傞偙偲偑偱偒偰丄
丂丂倶2亖(1/2-倱)2+(1/4-倱2)亖1/2-倱亖(32/3-31/3+1)/4亖 1/(31/3+1)
丂傛偭偰丄丂倶亖1/併(31/3+1)
偲側傝丄妋偐偵夝摎偵偁偭偨傕偺偲堦抳偱偡丅
乮僐儊儞僩乯丂偪傚偭偲寁嶼偺捛擣偑戝曄偱偡偹両偙偙偼丄傗偼傝朻摢偺夝偺傛偆偵慺捈偵寁
丂丂丂丂丂丂嶼偟偨曽偑丏丏丏偄偄偐傕丅
乮捛婰乯丂暯惉俀係擭俁寧侾侾擔晅偗
丂嬻廙偝傫丄桳擄偆偛偞偄傑偡丅偙偺倅偵拝栚偡傞偺偼嬌傔偰帺慠側棳傟偐偲丅偨偩丄偙偆偟偨
偙偲偵懡偔偺庴尡惗偺敪憐偑岦偐偆偐偳偆偐丠慺捈偵丄俹俻傪墑挿偱偒傞偐丄偙偙偱偡丅擄娭
戝妛庴尡惗偵偼乽忢幆乿側傫偱偟傚偆偐丠
丂恾宍検偺曄壔乮MAX丆min乯偼丄偦偺恾宍検傪娭悢偱懆偊偨嵺偺嬌戝丒嬌彫偵娭傢傞丅偙傟
偵娭楢偟偨傾僾儘乕僠偵丄偄傢備傞乽偼傒弌偟偗偢傝乿偲偝傟傞丄搶嫗弌斉悇彠偺曽朄偑偁傞
偐偲巚偄傑偡丅
丂乽嵟彫乮or嵟戝乯偲側傞恾傪梊應偟丄偦偙偐傜偺旝彫側曄壔傪専摙偟偰丄梊應偺崌棟惈傪妋
曐偡傞乿乮偍偍傛偦偺応崌丄柺愊傪2摍暘偡傞応柺偑懡偄丅廬偭偰慄暘斾偱偼丄侾丗![]() 側偳偑
側偳偑
昿弌乯
丂偙偙偱偺嬻廙偝傫偺夝朄傕嫟捠偡傞偺偱偼偲峫偊傑偡丅
丂乽偼傒弌偟偗偢傝乿偺婎杮揑妶梡椺偼丄愨懳抣婰崋晅偒偺2師娭悢偺僌儔僼偲尨揰捠夁捈
慄偺岎揰偱嶌傜傟傞晹暘偺柺愊検偺曄壔偺栤戣偱偟傚偆偐丅曻暔慄埲奜偱傕丄椺偊偽丄杮
2012擭偺戝妛擖帋栤戣偐傜偱傕丄搶嫗戝妛丒暥宯2斣丄搶岺戝丒3斣側偳偱桳岠側曽朄偩傠
偆偲丅
丂屄恖揑偵偼晄妋偐側弌揟偱偡偑丄墶昹崙戝丒2010擭偵弌戣偝傟偨暯柺儀僋僩儖偺栤戣丅
嵟戝妏120搙丄3曈偑俈丄俆丄俁偺挿偝偺嶰妏宍偺撪怱傪捠夁偡傞捈慄偱彫偝偄嶰妏宍傪嶌
傝丄偦偺柺愊検偺曄壔偺栤偄丅偙偙傜偁偨傝偵傕巊偊傞峫偊曽偐偲丅
丂偦傟偱丄偙偺搶杒戝妛偺栤戣偼丄偦偙偑妏搙偺旝彫側曄壔偵娭傢傞偲偄偆偙偲偑丄偄傢備
傞悢妛嘦抜奒偺旝暘傪挻偊傞偺偩傠偆偐偲巚偭偰偄傑偡丅
丂偁傞偄偼丄曄壔偡傞恾宍検偑丄2師揑乮2曄悢揑乯偑僞乕僯儞僌億僀儞僩側偺偐丅偁傞偄偼丄
曄壔偦傟帺恎偑憡帡丒奼戝丒弅彫揑偐丄夞揮揑偐偵埶懚偡傞偺偐丅
丂壗偐丄巹帺恎偑乽庴尡悢妛乿偺堦柺揑棟夝偺巙岦偺備偊偵丄傂偲傝柪偭偰偄傞姶傕偟傑偡丅
悢妛偺悽奅偱偼忢幆埲慜偺儗儀儖側偺偐偲巚偄偮偮丏丏丏丅
丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俁寧侾侾擔晅偗乯
丂旝暘偵傛傟偽丄摨條偵偟偰堦斒偵師偺傛偆偵側傝傑偡丅
丂墌偺尫AB傪偲傞丅墌廃忋偺掕揰C傪捠傞捈慄偑丄AB偲岎傢傞揰傪Q丄墌廃偲嵞傃岎傢傞揰
傪P偲偡傞丅PQ偑嵟戝偵側傞偺偼丄埲壓偺帪偱偁傞丅
丂P偐傜AB偵堷偄偨悅慄偺懌H偵偮偄偰丄H偲Q偺拞揰偑墌偺拞怱偲堦抳偡傞
丂懠偺応崌偑偙傟傛傝抁偔側傞偙偲傪婔壗揑偵徹柧偡傞偺偼壜擻偐傕偟傟傑偣傫丅弶摍婔壗
傪妝偟傓側傜峫偊偰傒傞偺傕椙偄偐傕偟傟傑偣傫丅
丂堦墳岆夝偑偁傞偲偄偗側偄偺偱曗懌偟傑偡丅
丂乽嵟彫乮or嵟戝乯偲側傞恾傪梊應偟丄偦偙偐傜偺旝彫側曄壔傪専摙偟偰丄梊應偺崌棟惈傪妋曐偡傞乿
丂乽偼傒弌偟偗偢傝乿偺婎杮揑妶梡椺偼丄愨懳抣婰崋晅偒偺2師娭悢偺僌儔僼偲尨揰捠夁捈慄偺岎揰偱嶌傜傟傞
丂晹暘偺柺愊検偺曄壔偺栤戣偱偟傚偆偐丅
丂S偺曄壔佮r2/2丒(兤偺曄壔)丂偲偄偆傛偆側彂偒曽偱偼妋偐偵尩枾偱側偄偺偱丄崌棟惈偺妋
曐偑昁梫偱偡丅
丂嬋慄傪嬌宍幃偱丄倰=倰(兤) 偲彂偗偽丄S偼丄倰2/2 偺掕愊暘丄偲偄偆偙偲傪巊偊偽丄
dS/d兤亖倰2/2丂傪摼傑偡丅偙傟偼尩枾偵惉傝棫偪傑偡丅偙偆媍榑偡傟偽崌棟惈偺妋曐偼晄
梫偱偡丅
丂崱夞偺椺偱傕丄堦斒偺嬋慄 倰=倰(兤) 偺揰P偱偺愙慄偲OP偺側偡妏兛傪兤偺幃偱昞偡偲丄
嬌尷寁嶼偱帵偝傟傑偡偑丄兛亖Arctan(倰(兤)/倰乫(兤))丅尵偄偐偊傞偲丄d倰/d兤亖倰/tan兛
偑
尩枾偵惉傝棫偪傑偡丅偟偨偑偭偰丄崌棟惈偺妋曐傪偡傞昁梫偼側偄偱偡丅乽偼傒弌偟偗偢傝乿
偼桳柤偱偡偑丄偙偺曈傝偑偨傇傫桳柤偱側偄偺偼巆擮偱偡...
丂俽乮俫乯偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀係擭俁寧侾侾擔晅偗乯
丂乽弶摍婔壗乿偱傾僾儘乕僠偲敪憐傪惂尷偣偢丄斞崅愭惗偼丄佢QPB偑怓乆側妏偱夝朄偼
傒傫側偪偑偭偰丄傒傫側偄偄偐傜偲泏惗偵懀偝傟傞偲丄埥傞泏惗=彮彈A 偝傫偑師偺傛偆偵
儗億乕僩偟偨丅
丂墌傪丄t--->(1/2)乮們倧倱倲丆倱倝値倲乯丄Q=乮X丆0乯 偲偟丄儀僋僩儖PB偲PQ偺撪愊傪峫偊師傪摼傞丅
丂倶亖併[(-(1/2) + 乮們倧倱t乯/2)2 + 乮倱倝値2t乯/4]丂丄倷亖併[(X - 乮們倧倱t乯/2)2 + 乮倱倝値2t乯/4]
(1/2 - 乮們倧倱t乯/2)丒(X - 乮們倧倱t乯/2) + 乮倱倝値2t乯/4
亖乮1/2乯併[(1/2 - 乮們倧倱t乯/2)2 + 乮倱倝値2t乯/4]丒併[(X - 乮們倧倱t乯/2)2 + 乮倱倝値2t乯/4]}
丂偙傟偐傜 X丄t 傪徚嫀偟丄
丂丂丂倶2(-4倶2+4倶4+4倶倷-4倶3倷-倷2+4倶2倷2)(-4倶2+4倶4-4倶倷+4倶3倷-倷2+4倶2倷2)=0
傪摼傞偙偲傪妋擣傪両偲丄斞崅愭惗丅
丂偙偺偲偒丄丂C 丗 -4倶2 + 4倶4 - 4倶倷 + 4倶3倷 - 倷2 + 4倶2倷2 = 0
丂乽-4*x^2 + 4*x^4 + 4*x*y - 4*x^3*y - y^2 + 4*x^2*y^2 乿傪乽Wolfram|Alpha乿偵憓擖偟偰丄
NormalVector 偑乮0丆1乯偵慄宆廬懏偐傜丄
{倶丆倷丆俲}={乮1/2乯併[1 - 31/3+32/3]丆乮1/4乯(1-31/3+32/3)3/2丆乮1/2乯32/3(1-31/3+32/3)3/2}
傪摼偰丄栤戣偺摎偊偼丄丂倶=乮1/2乯併[1 - 31/3 + 32/3]
丂挌擩側夝摎偩偑丄懠偺泏惗偵峴娫傪傕偆彮偟杽傔側偝偄偲斞崅愭惗偑懀偝傟偨丅偝傜偵丄
佢BPQ偑懠偺妏偺応崌偵丄偙傟傪摜廝偟偰堊偟側偝偄偲暿偺泏惗偵丅偦偟偰丄帺暘偼枹懱尡
偩偑丄4師戙悢嬋慄C偺憃懳嬋慄傪惀旕媮傔偰偔傟偲壽戣傪幩塭婔壗偲戙悢嬋慄丂嬋柺 ...偺
庴島惗偵丅奺泏惗偑弶懱尡偺桖墄傪姶偠偨偄偲捈偖庢傝慻傒巒傔偨丅
丂泏惗=彮彈A 偝傫偑摎偊偨俁昩屻偵丄彮彈B偝傫偑丄
丂{x = Sqrt[T^2/(1 + T^2)^2 + (-(1/2) + (1 - T^2)/(2*(1 + T^2)))^2],
丂y = Sqrt[T^2/(1 + T^2)^2 + (-((1 - T^2)/(2*(1 + T^2))) +
X)^2],
丂丂T^2/(1 + T^2)^2 + (1/2 - (1 - T^2)/(2*(1 + T^2)))* (-((1 - T^2)/(2*(1
+ T^2))) + X)
丂 = 1/2*Sqrt[T^2/(1 + T^2)^2 + (1/2 - (1 - T^2)/(2*(1 + T^2)))^2]
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂*Sqrt[T^2/(1
+ T^2)^2 + (-((1 - T^2)/(2*(1 + T^2))) + X)^2]}
偐傜丄{X丆T}傪徚嫀偟丄F[倶丆倷]=0 傪摼丄崯傟偼壜栺戙悢嬋慄屘丄堦偮偺場巕傪嵦梡偟丄
丂F1[倶丆倷]=0丄倶=1/2*Sqrt[1 - 3^(1/3) + 3^(2/3)]
偱偡偲丅偊偭? 側傫偱?側傫偱??? 偲丄彮彈A 傪娷傓懠偺泏惗丅
丂斞崅愭惗偑挻墇奼戝懱偺島媊傪堊偝傟偨偲偒丄帺庡揑偵挷傋丄栤戣傪峫嶡偟偨偱偟傚偆丅
乽僐儗傪偮偐偭偨偺傛乿丂彮彈B偝傫偺愢柧偵乽傔偑揰乿偵側傝丄懠偺泏惗偑峫偊偼偠傔偨丅
丂泏惗彅巵偑愢柧偝傟傞傑偊偵丄奆偝傫偑愢柧婅偄傑偡丅
丂泏惗=彮彈C偑婣傞傗斲傗惔乆偟偨昞忣偱崟斅偵僠儑乕僋壒傕寉傗偐偵彂偒楢偹偨丅斞崅
愭惗偑尋媶幒偵擖傞偲丄彮彈C偺忋偺婰嵹傪帇偰丄泏惗=彮彈C偺捠傝偵夝摎梡巻偵彂偄偨
傜嵦揰偟偰偄偨偩偗傞偺偐偟傜丠
丂斞崅愭惗偼丄泏惗払偺懳榖傪挳偒側偑傜丄崟斅偺乽I1=I2乿傪拲帇偝傟偰偍傜傟偨丅巚峫傪朩
偘偰偼偄偗側偄偲泏惗払丅擛壗側傞徹柧傪側偝傟偰偄傞偺偐拲帇偟偰偄偨丅
丂悢暘娫丄惷庘偑巟攝偟偨偑丄斞崅愭惗偑怳傝岦偄偰塢傢傟偨丅乽偪傚偭偲堦懅擖傟傞傛丅乿
丂僀僨傾儖偑摍偟偄偼棟榑偺側偐偱巊傢偸偲偒偼側偄偑丄攚宨傕棟榑忋偼抦幓偩偑丄崯張
傑偱嬶懱壔偟偨偺傪泏惗偑堊偟偨偺傪帇傞偺偼弶懱尡偱偡丅
丂泏惗払偐傜丄偦偺悢暘屻丄擬偄梫朷偑楢柤偱弌偝傟偨丅師夞偺島媊偐傜偼丄僀僨傾儖榑傪
拪徾戙悢泏偲塢傢偢丄崱夞偺泏惗=彮彈C偝傫偺傛偆偵丄嬶尰壔偟偨宍偱偍婅偄偟傑偡両乮島
嵗柤偼旕拪徾戙悢泏偲偟偰両)
丂崯張傪朘傟傜傟傞悽奅偺奆條傊偺偍婅偄丗
丂夝摎傪枴撉偝傟丄峴娫傪杽傔丄崯張偵夝愢偟偰壓偝偄丅傑偨丄偙偺傛偆側夝摎椺傪尒偐偗傜
傟偨傜惀旕偛嫵帵壓偝偄丅峏偵丄偍婅偄丅偙偺傛偆側栤戣傪採帵偝傟丄僀僨傾儖傪梡偄偰夝偄
偰崯張偵採帵偟偰壓偝偄丅
丂斞崅愭惗偑偳偆偟偰傕塢傢側偄偱偼偄傜傟側偄偲丄嵟屻偺戙悢嬋慄偑壜栺側偺偼傛偄偑丄
巊傢偸梋暘側Cj 偑嵼傞丅偦傟傪傓偞傓偞幪偰嫀傞嫮屌側棟桼傪榑偠側偝偄偲丅
乮捛婰乯丂暯惉俀係擭俁寧侾俁擔晅偗
丂嬻廙偝傫丄俽乮俫乯偝傫丄偄偮傕屼嫵帵偁傝偑偲偆偛偞偄傑偡丅
丂嬻廙偝傫偺夝朄丅嬌宍幃丄妏搙偱偺旝暘偁偨傝偼丄彫惗慡偔枹抦側傫偱偡丅寛偟偰棟桼偵
側傝傑偣偸偑丄彫惗偑崅峑惗偱偁偭偨偙傠偼丄偄傢備傞乽斖埻奜乿偩偭偨偐偲丅擭楊憌偑摿
掕偱偒偦偆偱偡偑丅偦傫側偙偲偼丄偦傟偙偦乽栤戣奜乿丅帺恎偱妛傋偽偄偄偺偱偡偑丄枹偩庤
偮偐偢偱偡丅帺傜偺恎偺忎偵偁偭偨傾僾儘乕僠偱峫偊偨偄偲巚偄傑偡丅
丂偙偺搶杒戝妛偺栤戣偺乽夝乿偺峔恾偑丄
丂丂P偐傜AB偵堷偄偨悅慄偺懌H偵偮偄偰丄H偲Q偺拞揰偑墌偺拞怱偲堦抳偡傞
旕忢偵嫽枴怺偄偱偡丅傕偆彮偟丄巹側傝偺乽弶摍婔壗乿偱峫偊偨偄偲巚偄傑偡丅
丂偄傢備傞乽偼傒弌偟偗偢傝乿偺偙偲偵偮偄偰傕丄乽尩枾側媍榑乿乽崌棟惈偺妋曐乿傪婇恾偡傞
側傜丄嬻廙偝傫偺偛巜揈偼丄偳偺傛偆側栤戣偵傕捠偠傞偺偱偼側偄偐偲傕丅偙偙傜偁偨傝傕杮
擭偺搶戝丒暥宯2斣側偳傪慺嵽偵峫偊偨偄偲巚偄傑偡丅
丂S(H)偝傫偺乽傒傫側偪偑偭偰偄偄乿偲偄偆偙偲丅傑偝偟偔偱偡丅vector丄撪愊偐傜弌敪偟偰丄係
師曽掱幃偵婣拝丅偦傟偼乽幩塭婔壗乿偺悽奅偵楢側傞摴嬝丒丒丒丅偦傫側晽偵搳峞傪攓撉偟
傑偟偨丅乽幩塭婔壗乿丄偙傟傑偨彫惗偵偼尵梩偺傒偺悽奅偱偟偰丒丒丒丅偨偩丄vector偱峫偊傞
偲偄偆偙偲偵偼嫽枴偁傝傑偡丅乮柕弬偟偨昞尰偱偟傚偆偐丠乯
丂夵傔偰丄奆偝傫偺搳峞傪撉傑偣偰偄偨偩偔偲丄愱栧惈偺崅偄媍榑傪揥奐偝傟偰偄傞偺偩傠
偆偲憐憸偟傑偡丅乮僣儞僪僋偵廔傢偭偰偄傑偡丄彫暯朚旻挊亀婔壗傊偺桿偄亁偺儁乕僕傪傔偔傠
偆偐偲巚偭偨傝偡傞偙偺偙傠偱偡乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂