
一つの固定された円Aの周りを滑らずに接しながら円Bが回転する。接点Pで下図のよ
うであった模様は、接点Qにおいては、どのようになるであろうか?
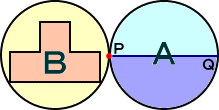
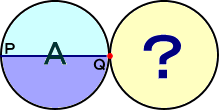
(答) 理論的には、外サイクロイドの話であるが、これはパズルなので、実際にやってみた
方がいいだろう。
正解は、
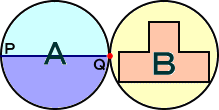
模様が、上下逆になると思った方はいませんか? (参考:丸太での移動)
(追記) 令和3年4月1日付け
上記で、「実際にやってみた方がいいだろう」と書いたが、実は計算で簡単に求められるこ
とに最近気づいた。
例えば、半径 r の円が進む距離PQは、円の中心が移動する距離OO’に等しい。
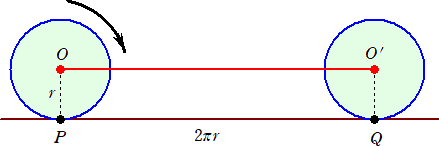
このことを円周上で考える。円A、Bの半径を r とすると、円Bの中心の移動距離は、
2π×2r=4πr である。一方、円Bの円周の長さは、2πr なので、円Bは、円Aの周りを、
4πr÷2πr=2(回転) することになる。
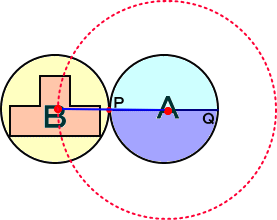
このことから、必然的に、正解が、1回転に相当する場合なので、

となることは理解できると思う。
読者のために練習問題を残しておこう。
練習問題 下図において、円O、半円Q、Rの半径を r とし、線分AD、BCの距離は、円O
の円周の長さと同じとする。
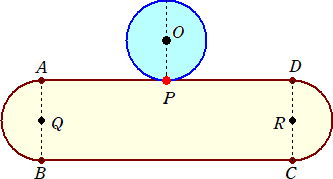
このトラックを円Oが滑らずに回転して一周するとき、果たして何回転するだろうか?
(解) 円Oの中心の移動距離は、 2πr×2+π(r+r)×2=8πr
よって、 8πr÷2πr=4(回転) することになる。 (終)