
割合という概念は、小学校の算数で最も難しい単元といわれる。「比べられる量が、もとに
なる量の何倍であるかを示す量である。」とすんなり理解されれば問題は起こらないが、単
位のない量ゆえ、児童にとっては、まごつく概念である。
もとになる量を A、比べられる量を X とすると、通常、割合といった場合、X/A を考える
のが普通である。
これに対して、最近、X/(A−X) という割合の考え方があることを知った。
X/A のような、(部分)/(全体)の割合は、ある瞬間における割合をみる場合は適当であ
るが、X がどのように変化したのかをみたい場合は、X/(A−X) のような、(部分)/(残り)
の割合を考えた方が都合がよいらしい。
例えば、有病率とは、ある時点、ある地域内の全患者数をその地域の人口で割ったもの
を指すが、この考え方は、前者である。これに対して、罹患率とは、一定期間に発生した特
定の疾病の新患者数の、その疾病にかかる危険にさらされた人口に対する比率のことで、
これは、後者の考え方である。
例 ある国の人口は、A 人である。いま、この国は、ある伝染病に汚染され、現在、X 人の
人が罹患している。これらの保菌者は、現在のところ、全く隔離されていない。一人の保
菌者が、非保菌者と接触して非保菌者が罹患する割合(伝染率)を p として、患者の増
加する変化の状態を把握したい。
上の条件から、次のような微分方程式が成り立つ。
この微分方程式を解けば、(解法については、こちらを参照)
となる。ただし、C は初期条件より定まる任意定数である。
上の式からも分かるように、X/(A−X) は指数的変化をし、対数方眼紙を用いることに
よって、そのグラフは直線化され、より正確に変化の状態を把握することができる。
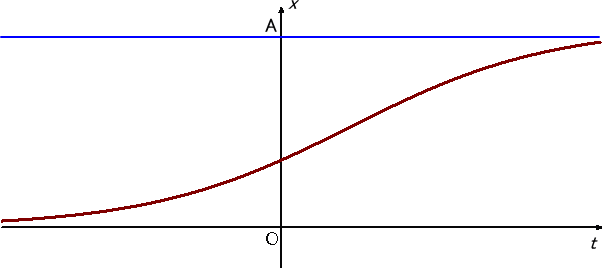
実際の X の変化の様子は、
のグラフから、次のようである。
(参考文献:森 毅 著 指数・対数のはなし (東京図書))