
私の備忘録「5の倍数」における問題を考えるとき、その背景には深遠なる数論の世界
が横たわるのを感じざるを得ない。ここでは、その話題を代数学的に、もう少し詳しく考え
てみようと思う。
p 進整数を説明するために、p進法展開された数 anan−1an−2・・・a1a0 (p) が
anpn+an−1pn-1+an−2pn-2+・・・+a1p+a0 (各akは、0≦ak<p なる整数)
すなわち、
a0+a1p+・・・+an−2pn-2+an−1pn-1+anpn (各akは、0≦ak<p なる整数)
と表されることを確認しておこう。
これを、p のべき級数で表したもの:
a0+a1p+・・・+an−2pn-2+an−1pn-1+anpn+・・・
(各akは、0≦ak<p なる整数)
を、p 進整数と言うようだ。
これら p 進整数全体から、p 進数体 Qp が構成される。(詳しい議論は割愛!)
実数の中で、有理数全体は稠密に存在しているが、隙間だらけでもある。その隙間を埋
めることを完備化という。完備化の有名な方法としては、「デデキントの切断」(2つの数の
順序に注目した方法)や「距離空間における収束点列」(2つの数の距離に注目した方法)
がある。p 進数体 Qp は、有理数体Qの完備化になっているらしい。
この原稿を書きながら、大学院入試での口頭試問のことが頭をよぎった。ある先生から
「p 進整数について、・・・。」と質問されてしまったのだ。それについてあまり準備していな
かったものだから、ドッと冷や汗が出てしまった。何を答えたか、よく覚えていない。なぜか
その部分の記憶が空白のままである。せめてもの罪滅ぼしに、p 進整数のことをまとめよ
うと思い至ったこともこのページを起こそうとした一つの要因である。
さて、私の備忘録「5の倍数」における問題は、
どのような自然数 n に対しても、
x2+1 が、5n の倍数となるような自然数 x が存在する
つまり、
任意の自然数 n に対して、ある自然数 xn が存在して、xn2+1 は、5n の倍数
というものであった。
その解は、 x1=2 、 x2=7 、x3=57 、x4=182 、・・・ であるが、何の脈絡も
なく、これらの数字が存在するはずがない。
私の備忘録「5の倍数」における構成を整理すると、 xn から、xn+1 を求めるには、
(xn2+1)/5n を 5 で割った余りを an として、
漸化式 xn+1=xn+5n・an (n=1,2,3,・・・)
により、帰納的に定めればよい。
実際に、 x1=2 に対して、 (x12+1)/5=1 を 5 で割った余りは、 a1 =1 なので、
x2=x1+5・a1=2+5=7
(x22+1)/52=2 を 5 で割った余りは、 a1 =2 なので、
x3=x2+52・2=7+50=57
・・・・・・・・・・・・・・・・・・・・
ところで、上式を 5進法展開風に表示させてみよう。
すなわち、 x1=2 → x1 に対して、 x12+1≡0 (mod 5)
x2=2+1・5 → x2 に対して、 x22+1≡0 (mod 52)
x3=2+1・5+2・52 → x3 に対して、 x32+1≡0 (mod 53)
・・・・・・・・・・・・・・・・・・・・・・・
いま、 x1=2 に対して、 x12=4≡−1 (mod 5) なので、
(x12)5≡(−1)5=−1 (mod 5)
一方、 (x12)5+1=(x12+1){(x12)4−(x12)3+(x12)2−x12+1} において、
x12+1≡0 (mod 5) かつ
(x12)4−(x12)3+(x12)2−x12+1≡5≡0 (mod 5)
であるので、 (x12)5+1≡0 (mod 52) も成り立つ。
つまり、 (x15)2+1≡0 (mod 52) が成り立つわけである。
このことから、 x2≡x15≡25 (mod 52) と考えてよい。
後は帰納的に、 x3≡x25≡25^2 (mod 53) 、・・・・ と定められる。
一般に、
xn≡xn−15≡25^(n−1) (mod 5n)
であるといえる。
実際に、 x1=2
x2≡25=32≡2+1・5 (mod 52)
これは、通常の素因数分解の方法により簡単に得られる。
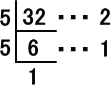
上記の計算から、 32=2+1・5+1・52 であるが、
x2≡32≡2+1・5 (mod 52)
である。
同様にして、
x3≡25^2=225 (mod 53=125) において、
225=(27)3・24≡33・24
=27・16=432≡57 (mod 53=125)
よって、 57=2+1・5+2・52 であるが、
x3≡2+1・5+2・52 (mod 53=125)
読者のために、一つ演習問題を残しておこう。
問題 25^3≡a0+a1・5+a2・52+a3・53 (mod 54) となる {an} (0≦an<5)を決
定し、それが、x2+1≡0 (mod 54)の解になることを確かめよ。
この問題を考えるために、上記の求め方の別解を考えてみる。
x1=2 は、正しくは、 x1=2 (mod 5) である。
よって、 x1=2+k・5 (k は整数) と書ける。
このとき、 x2≡x15=(2+k・5)5≡25+5・24・k・5≡32≡2+1・5 (mod 52)
同様にして、 x2≡2+1・5 (mod 52) より、 x2=2+1・5+k・52 (k は整数)
と書ける。 このとき、
x3≡x25=(2+1・5+k・52)5≡(2+1・5)5+5・(2+1・5)4・k・52 (mod 53)
≡(2+1・5)5 (mod 53)
≡25+5・24・5+10・23・52 (mod 53)
≡32+16・52 (mod 53)
≡(2+1・5+1・52)+1・52 (mod 53)
≡2+1・5+2・52 (mod 53)
以上を踏まえて、問題は次のように解かれる。
(解) x3≡2+1・5+2・52 (mod 53) より、
x3=2+1・5+2・52+k・53 (k は整数)
と書ける。このとき、
x4≡x35=(2+1・5+2・52+k・53)5
≡(2+1・5+2・52)5+5・(2+1・5+2・52)4・k・53 (mod 54)
≡(2+1・5+2・52)5 (mod 54)
≡(2+1・5)5+5・(2+1・5)4・2・52 (mod 54)
≡25+5・24・5+10・23・52+5・24・2・52 (mod 54)
≡32+16・52+16・53+32・53 (mod 54)
≡(2+1・5+1・52)+(1+3・5)・52+(1+3・5)・53+(2+1・5+1・52)・53
(mod 54)
≡2+1・5+1・52+1・52+3・53+1・53+2・53 (mod 54)
≡2+1・5+2・52+1・53 (mod 54)
いま、 x32≡−1 (mod 53) なので、 x32+1≡0 (mod 53)
また、 (x32)4−(x32)3+(x32)2−x32+1≡5≡0 (mod 5) なので、
(x32+1){(x32)4−(x32)3+(x32)2−x32+1}≡0 (mod 54)
よって、 (x32)5+1≡0 (mod 54) すなわち、(x35)2+1≡0 (mod 54)が成り立つ。
x4≡x35 (mod 54) なので、 x42+1≡0 (mod 54) となる。(終)
もちろん、力任せに次のように解いてもよい。
(別解)
25^3=2125=(213)9・28≡679・256=(672)4・67・256≡(114)4・277
≡(−129)2・277≡391・277≡182≡2+1・5+2・52+1・53 (mod 54)
後半部分は、上記の解と同様である。(終)
以下、工事中