
中学レベルの計算力から高校レベルの計算力に引き上げる方法として、「式の計算」が最
適である。乗法公式にせよ、因数分解にせよ、計算を簡略化するためには、しっかりした洞
察力が必要である。結論までの道筋を考えずに計算を始めるのは、当てもなく砂漠をさまよ
うようなものである。その意味で、着実な計算力を身につける場が、「式の計算」分野である。
高校以降に使うであろう乗法公式、因数分解は、それほど複雑なものは必要ない。「式の
計算」で学ぶ乗法公式、因数分解の複雑なものは、計算力増強のためにだけあるといって
も過言ではない。
練習問題として、次の問題を考えて欲しい。多分、計算が煩雑という意味で、難問の部類
に入ると思う。
問題 XY+YZ+ZX=1 のとき、次の等式が成り立つことを示せ。
最初、「条件式は、文字の消去に使え」という鉄則に従い、次のように計算してみた。
条件式より、X(Y+Z)=1−YZ なので、
左辺−右辺を通分し、その分子A に上式を代入して整理すると、
A=X(1−Y2)(1−Z2)+Y(1−Z2)(1−X2)+Z(1−X2)(1−Y2)−4XYZ
ここで、
B=(1−YZ)(Y+Z)(1−Y2)(1−Z2)+Y(1−Z2)((Y+Z)2−(1−YZ)2)
+Z(1−Y2){(Y+Z)2−(1−YZ)2}−4YZ(1−YZ)(Y+Z)
第1項と第4項、第2項と第3項を組み合わせて計算すると、
B={(1−YZ)3(Y+Z)−(1−YZ)(Y+Z)3}+{(1−YZ)(Y+Z)3−(1−YZ)3(Y+Z)}
=0
よって、左辺−右辺=0 となり、等式は成り立つ。
(注) 上記の計算からは窺い知れないかもしれないが、途中の計算は、かなりハードであ
る。式の展開から、平方の和に変形する洞察力が要求される。
上記のような計算を反省してみると、この計算のトリックが見えてくる。そこで、次のような
解法が思いつく。(ポイントは、Xの係数を平方の和に表すこと。)
左辺−右辺を通分し、その分子を、A とすると、
A=X(1−Y2)(1−Z2)+Y(1−Z2)(1−X2)+Z(1−X2)(1−Y2)−4XYZ
=X2{Y(Z2−1)+Z(Y2−1)}+X{(1−Y2)(1−Z2)−4YZ}+Y(1−Z2)−Z(1−Y2)
=X2(YZ−1)(Y+Z)+X{(YZ−1)2−(Y+Z)2}−(YZ−1)(Y+Z)
={X(Y+Z)+(YZ−1)}{X(YZ−1)−(Y+Z)}
=(XY+YZ+ZX−1)(XYZ−X−Y−Z)
=0
よって、左辺−右辺=0 となり、等式は成り立つ。
(注) 因数分解の基本原則:「次数が同じ文字の場合は、1つの文字に着目して式を
まとめよ」に従った解法であり、洞察力のある方は、こちらの解法をまず思い浮かべ
るかもしれない。
ところで、このような問題は、どのようにして作られるのだろうか?
上の計算で、
というのがあった。
この式を、ボンヤリ眺めていると、三角関数における正接の加法定理に似ていることに
気がつく。加法定理から、
両辺の逆数をとって、
この式から、次の式も成り立つ。
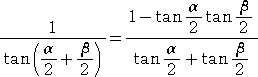
いま、α+β+γ=π とすると、

したがって、
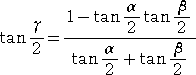
が成り立つ。
この式は、まさしく、
そのものである。
したがって、条件式 XY+YZ+ZX=1 は、実は三角形における次の関係式から得られ
る。
三角形の3つの内角を、α、β、γ とすると、
また、三角形においては、次の関係式も有名である。
三角形の3つの内角を、α、β、γ とすると、
(証明は、こちらを参照)
正接の2倍角の公式より、
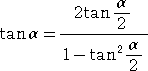
が成り立つ。
(
このことから、
とおくと、
である。
したがって、
は、
そのものであることが分かる。
このように一見して関係がないような、問題のための式と思いきや、実は、三角関数の
世界に翻訳してみると、(仮定)、(結論)ともに、三角形において常に成り立つ式であるこ
とに驚きを感じる。問題作成の原点を見た思いである。
(参考文献:浅見 汎 著 ヘロンの公式を導く(啓林 高数編 No.205) (啓林館))