格子状に、５×５の点がある。これらの点を結んで正方形を作るとき、異なる面積を持つ
正方形は何種類できるか？

　　

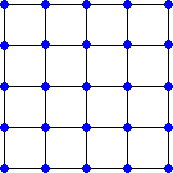
　日能研の車内パズルでも最近同じような問題を見たような気がする。答えは、面積が

　　１　、２　、４　、５　、８　、９　、１０　、１６

と８種類あることは直ぐ分かるだろう。

　　

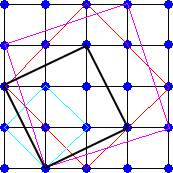
　ここで、何となく気づくことがある。それは、８個の面積の値を、４を法として考えると、順に

　　１　、２　、０　、１　、０　、１　、２　、０

となり、「３」が出現しないことだ。

　一般に、２つの整数 ａ、ｂ に対して、三平方の定理から、ａ²＋ｂ² により、正方形の面積が
求められる。

　ａ が偶数ならば、　ａ²≡０　（ｍｏｄ　４）　、ａ が奇数ならば、　ａ²≡１　（ｍｏｄ　４）

　ｂ が偶数ならば、　ｂ²≡０　（ｍｏｄ　４）　、ｂ が奇数ならば、　ｂ²≡１　（ｍｏｄ　４）

なので、ａ、ｂ の偶奇をどのように組み合わせても、４を法として　ａ²＋ｂ²≡３ になることは
ない。

　さらに、気づくことがある。それは、

　２×４＝８　、２×５＝１０　、２×８＝１６

からも分かるように、面積の数同士を掛けてまた面積の数が得られることだ。

　これは、ｉ を虚数単位として、ａ²＋ｂ²＝（ａ＋ｂ・ｉ）（ａ−ｂ・ｉ）、ｃ²＋ｄ²＝（ｃ＋ｄ・ｉ）（ｃ−ｄ・ｉ）
と表せるので、

　（ａ²＋ｂ²）（ｃ²＋ｄ²）＝（ａ＋ｂ・ｉ）（ａ−ｂ・ｉ）（ｃ＋ｄ・ｉ）（ｃ−ｄ・ｉ）
　　　　　　　　　　　　　＝（ａｃ−ｂｄ＋（ａｄ＋ｂｄ）ｉ）（ａｃ−ｂｄ−（ａｄ＋ｂｄ）ｉ）
　　　　　　　　　　　　　＝（ａｃ−ｂｄ）²＋（ａｄ＋ｂｄ）²

となることから明らかだろう。

　以上を考えると、次の事実が具体例を通して実感できると思う。

　方程式 ｘ²＋ｙ² ＝ ｐ　（ｐ≠２）の解があるとする。　ｐ は、奇数なので、ｘ または ｙ のうち
一方は偶数、他方は奇数である。このとき、ｐ は、４で割って、１余る数である。

　このことは、４で割って、３余る有理素数 ｐ に対して、ａ²＋ｂ²＝ｐ を満たす ａ、ｂ が存在
しないことを意味し、

　　　　　４で割って、３余る有理素数 ｐ は、ガウスの整数としても素数

となる。（→　参考：「２次体の整数論」の「整数論の基礎知識」）