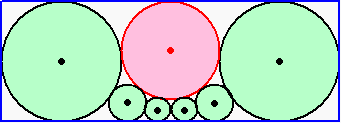
長方形の中の円の数によって、赤円(中央)と左端(右端)の黒円の半径比が決まるそう
です。これをダウンロードして数式をみたら、この比率が下記のようになっていました。
n は円の総数で、n≧3 とする。このとき、
黒円(両端)の半径:赤円の半径=2:(1+cos(2π/n)
確かに、これでGeoGebraで再現出来たのですが、理屈が判りません。普通に考えると数
学的帰納法をつかうのかなと思いましたが、一般解にたどりつく事ができませんでした。
題名から見て算額の問題のようですが、この証明方法をお教え下さい。作者に質問しよう
としましたがアドレスが判らず確認出来ませんでした。
こちらのお力を借りたく掲示板に掲載しましたので、よろしくご教示下さい。
DD++さんからのコメントです。(平成28年1月14日付け)
綺麗な解法がありそうだと昨日から考えているんですが、なかなか難しいですね。
DD++さんからのコメントです。(平成28年1月15日付け)
全ての円の半径の予想がつき、実際に証明できました。[ ] は添え字と思ってください。
間隔が 2 である平行線 L0 と L1 を考えます。以下、円は全てこの平行線の間に描くもの
とします。
0<θ<π/2 として、L0 に接する半径 r[F] = cos2θ の円 C[F] を描きます。その中心 F
から L1 に下ろした垂線の足を T[0] とします。
直線 L1 に接し、同時に C[F] に外接するような任意の円は、半径が sin2θ 以上であるは
ずです。よって、そのような円の半径は 0≦α<π/2 である実数 α を用いて、
r[α]= sin2θsec2α
と書けます。そのときの円を C[α]、C[α] の中心を P[α]、C[α] と L1 との接点を T[α] と
表すことにします。(T[0] の定義もこれと矛盾しません)
P[α] から直線 FT[0] に垂線を下ろして考えると、三平方の定理より
T[0]T[α]2 = ( r[F]+r[α] )2 - ( 2-r[F]-r[α] )2
= 4( r[F]+r[α]-1 )
= 4( cos2θ + sin2θ sec2α - 1 )
= 4( -sin2θ + sin2θ sec2α )
= 4 sin2θ ( sec2α - 1 )
= 4 sin2θ tan2α
つまり、 T[0]T[α] = 2 sinθ tanα となります。
α+θ<π/2 の場合に、円 C[α] と円 C[α+θ] を同時に描くことを考えます。ただし、
T[α] と T[α+θ] が L1 上で T[0] から見て同じ側に来るようにします。
このとき、
T[α+θ]T[α] = T[0]T[α+θ] - T[0]T[α]
= 2 sinθ tan(α+θ) - 2 sinθ tanα
= 2 sinθ sec(α+θ) secα { sin(α+θ) cosα - cos(α+θ) sinα }
= 2 sin2θ sec(α+θ) secα
= 2 √( r[α+θ]r[α] )
ですので、三平方の定理より
P[α+θ]P[α]2 = T[α+θ]T[α]2 + ( r[α+θ]-r[α] )2
= 4r[α+θ]r[α] + ( r[α+θ]-r[α] )2= ( r[α+θ]+r[α] )2
したがって、円 C[α] と円 C[α+θ] は互いに外接していることがわかります。
これを踏まえて、題意の通りに n 個の円を並べることを考えます。正確にはその右半分だ
け考えます。
n が偶数の場合、L1 に接する n-1 個の円のうち最小のものは C[0] になり、その隣は
C[θ]、さらに隣は C[2θ]、……となり、一番端は C[(n-2)θ/2] となります。
n が奇数の場合、T[0]T[α]=r[α] から sin2α=sinθ つまり α=θ/2 となるので、L1 に
接する n-1 個の円のうち最小のものは C[θ/2] になり、その隣は C[3θ/2]、さらに隣は
C[5θ/2]、……となり、一番端は C[(n-2)θ/2] となります。
いずれにせよ、一番端は C[(n-2)θ/2] となり、これが L0 にも接するので r[(n-2)θ/2] = 1
つまり、 cos{(n-2)θ/2} = sinθ から nθ/2 = π/2 すなわち θ=π/n
よって、問題の黒円と赤円の半径の比は、 1 : cos^2 (π/n) であることが示されました。
(半角の公式を使えば UIN さんの書いたものになりますが、こちらの方が綺麗なのではないかと)
補足として、全ての円の中心 P[α] は一つの放物線上に並び、その頂点は P[0]、焦点は
F です。これと放物線の性質、双曲線の性質を使ってどうにかできればエレガントな証明も
できそうですが、私はいろいろ試した末に諦めました。
GAI さんからのコメントです。(平成28年1月15日付け)
中央に描かれた赤い円の半径をすべて1としたとき、各nに於いて、すべての円が納まって
いる長方形の縦と横の長さをcos(2π/n)の数値を元に調べてみました。
n: 縦: 横: 横/縦:
3: 8: 16: 2=1+√1:
4: 4: 4(1+√2): 1+√2=1+√(2+√4)/2):
5: 4(3-√5): 8: (3+√5)/2=1+ √(3+√5)/2):
6: 8/3: 8(1+√3)/3: 1+√3:
7: cos(2π/7)が√で表せないので未結果
8: 4(2-√2) : 4(2-√2+√2(2-√2))) : 1+√(2+√2))=1+√(4+√8)/2):
9: cos(2π/9)が√で表せないので未結果
10: 4(5-√5)/5: 4(1-√5/5+√(2(1-√5/5))) : 1+√(5+√5)/2):
縦、横比が規則を作れそうで統一的なものには至りませんでした。私もGeoGebraをインス
トールしてこの算額の動きをやってみました。
まさにn=3〜16を変化させ、現れる図形をそれぞれ印刷してみると、すべて中央の赤の円
は半径1(cm)で描かれており、この時の長方形の縦、横を物差しで計測してみたら上記の数
値に対応するcmとなりました。
黒円(両端)の半径:赤円の半径=2:(1+cos(2π/n))
を証明しようとしましたがまったく歯が立たず、別の調査に走りました。
(DD++さんが成功されたみたいですので、ゆっくり鑑賞したいです。)
DD++さんからのコメントです。(平成28年1月16日付け)
「縦横比から1引いて2で割ってみたら……」とか思ってみたり。
UINさんからのコメントです。(平成28年1月16日付け)
DD++さん、GAIさん、ありがとうございます。GeoGebra並びに2D-CADで確認した所、図の
ような性質がありそうです。これは黒円同士の接点、両端の黒円と長方形の上辺との接点
が同一円上に有りそうです。
ほんの数個の図形で試したので、又ソフトの有効数字の限界もありそうですので確信は出
来ていません。
なお、この円(青表示)の中心は、赤円と長方形の上辺との接点になっているようです。こ
の性質(?)は証明に使えそうでしょうか?
空舟さんからのコメントです。(平成28年1月16日付け)
反転すると良い視点が得られるかもしれないと思いました。
→ 参考:「反転とその応用」、「反転」、「曲率の真実(反転)」
追記: xy平面に緑の単位円 x2+y2=1 を描く。それの外側に接するn個の黒い円を描く。
そのうちの1つは(0,1)で緑の円に接するようにしておく。
黒い円の中心は正n角形の頂点をなし、単位円に内接する正n角形と比較することで、その
半径rは、 1:2sin(π/n) = (1+r):(2r) の関係がある。r/(1+r) = sin(π/n) としてあとで使う。
黒い円たちに外接する赤い円を描く。原点中心で半径が1+2rの円である。
これらの図形を、(0,1)を中心とする反転円により反転する。(反転円の半径は2としておく)
緑の円は 直線y=0に移る。赤の円は (0,(1+r)/r),(0,r/(1+r)) を直径とする円に移る。黒い円
の1つは直線 y=(1+r)/r に移り、残りの黒い円が赤と緑および互いに接する円たちとなる。
そのときに一番大きい黒い円と赤円の直径の比は、
(1+r)/r : {(1+r)/r-r/(1+r)}= 1/sin(π/n) : 1/sin(π/n)-sin(π/n)
= 1 : 1-{sin(π/n)}2= 1 : (cos(π/n))2= 2 : {1+cos(2π/n)}
n = 反転する前の黒い円の数= 反転した後の黒い円の数 + 1
UINさんからのコメントです。(平成28年1月16日付け)
空舟さん、ありがとうございます。GeoGebraでは円による反転が簡単に出来るので、図を
描いて説明文をフォローさせて頂きます。
GAIさんからのコメントです。(平成28年1月16日付け)
n→∞となった場合を考えたら、2:(1+cos(0))=2:2=1:1に近づき、結局長方形(1:3の縦、
横の大きさ)に同じ大きさの3つの円が接した状態で並んでおり、下の隙間に無数の中央
の円と下の枠のラインと接している小円群が連なっている状態が起きる。
この極限の状態はファレイ数列と同じことが起こっているような気がしました。
長方形の下のラインをx軸、中央の円(半径1/2の赤い円に相当)の中心が(1,1/2)、左の
同じく半径1/2の円の中心を(0,1/2)<y軸上にとっている>と座標をとると、2つの円は(1/2,1/2)
で接する状態となる。
このとき、x軸上の1/2,2/3,3/4,4/5,・・・・,(n-1)/n では、
半径1/(2*2^2),1/(2*3^2),1/(2*4^2),1/(2*5^2),・・・・,1/(2*n^2) 即ち、1/8,1/18,1/32,1/50,
・・・・,1/(2*n^2)の大きさの円を
(1/2,1/8),(2/3,1/18),(3/4,1/32),(4/5,1/50),・・・・,((n-1)/n,1/(2*n^2))
を中心に描くと、無限に算額が主張する円が描けていける。
DD++さんからのコメントです。(平成28年1月16日付け)
そうです、無限に多い場合はフォードの円そのものです。sin2θ sec2α という式を私が予
想したのもまさにそこから。
