小学校２年で九九を習って、数学への長く遠い茨の道が始まる。ある者は、できるまで
居残り指導なんていうのも昔はあった。最近新聞紙上では、日本の児童・生徒の学力低
下が叫ばれている。何をもって学力とするかは、判断の分かれるところだが、少なくとも、
計算力に限定すれば、確実に、その力は落ちている。繰り返しの計算練習、居残り指導
などが軽視され、児童・生徒は、その学年で学ぶことを完全に修得しないまま、上級学年
に進級している。その積もり積もったツケのために、結局は、本人が苦しむわけであるが、
気づくのが遅かったために、進路変更せざるをえない場合もある。
誰が何と言おうと、計算の基本は、九九だろう。その九九が危機に瀕している。九九を
常習的に間違える高校生が少なからずいるのだ。
日本では、「に〜いちがに、ににんがし、にさんがろく、にしがはち、・・・」と、口と耳を使
って、割と語呂よく覚えられるようになっている。多少いいにくい段もあるが、前後を変え
れば、何とか間違えずに全段いえる筈だ。九九の完全習得が、小学校卒業の最大の条
件だろうと、私は思う。 ところで、アメリカなどでは、日本のような覚え方はないそうだ。
|
小学校２年相当で、「Ｔｉｍｅｓ Ｔａｂｌｅ」なるものを使って九九を覚えると、知り合いのアメリカ
人の方から伺った。（上図参照）
１個１個について、例えば、「２×３＝６」は、「Ｔｗｏ ｔｉｍｅｓ ｔｈｒｅｅ ｉｓ ｓｉｘ．」という が、
これでは、九九全部を覚えるのは容易でない、と感じるのは、私だけだろうか？
（追記） 令和元年１１月１９日付け
九九というと、８１通りの式を覚えるものと相場が決まっているが、江戸時代の九九は省
力化が図られ、３６通りだけを覚えればよかったらしい。そんなことが、吉田光由 著の「塵
劫記」にまとめられている。覚える部分は太字になっているところだけである。
| ２ | ３ | ４ | ５ | ６ | ７ | ８ | ９ | |
| １ | ||||||||
| ２ | ４ | ６ | ８ | １０ | １２ | １４ | １６ | １８ |
| ３ | ９ | １２ | １５ | １８ | ２１ | ２４ | ２７ | |
| ４ | １６ | ２０ | ２４ | ２８ | ３２ | ３６ | ||
| ５ | ２５ | ３０ | ３５ | ４０ | ４５ | |||
| ６ | ３６ | ４２ | ４８ | ５４ | ||||
| ７ | ４９ | ５６ | ６３ | |||||
| ８ | ６４ | ７２ | ||||||
| ９ | ８１ |
世界には、もっとすごい国がある。インドでは、２２×２０までの、いわゆる「九九」の表が
ある。
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
インドの人は、この４４０個の値を、本当に丸暗記するのだろうか？ここら辺の事情に詳しい
方、是非お教えください。（メールは、こちら）
最近、次のような速算術があることを知った。
例えば、１８×１９＝（１８＋９）×１０＋８×９＝２７０＋７２＝３４２
普通に計算して、１８×１９＝１８×９＋１８×１０＝１６２＋１８０＝３４２ とする場合に比べて、
３桁同士の足し算が、３桁と２桁の足し算に改良されているところが、若干「速い」ところなの
だろう。
数学の学習では、平方数の計算が頻出である。（平方根の計算、三平方の定理、余弦定
理、・・・） インドのように、２２×２０までの「九九」を覚えることは必要ないと思うが、１１から
１９までの平方数については、私自身の経験から言えば、多分知らないよりは知っている方
が得する場合が多いだろう。（速算術を用いると、容易に覚えられると思う。）
（→ 参考：「平方数を秒算する技」）
１１×１１＝１２１ ・・・・・ （１１＋１）×１０＋１×１＝１２０＋１＝１２１
１２×１２＝１４４ ・・・・・ （１２＋２）×１０＋２×２＝１４０＋４＝１４４
１３×１３＝１６９ ・・・・・ （１３＋３）×１０＋３×３＝１６０＋９＝１６９
１４×１４＝１９６ ・・・・・ （１４＋４）×１０＋４×４＝１８０＋１６＝１９６
１５×１５＝２２５ ・・・・・ （１５＋５）×１０＋５×５＝２００＋２５＝２２５
１６×１６＝２５６ ・・・・・ （１６＋６）×１０＋６×６＝２２０＋３６＝２５６
１７×１７＝２８９ ・・・・・ （１７＋７）×１０＋７×７＝２４０＋４９＝２８９
１８×１８＝３２４ ・・・・・ （１８＋８）×１０＋８×８＝２６０＋６４＝３２４
１９×１９＝３６１ ・・・・・ （１９＋９）×１０＋９×９＝２８０＋８１＝３６１
（参考文献：樺 旦純 著 数学がらくにわかる本（三笠書房））
（追記） 令和２年１２月２９日付け
平方数の覚え方を考えてみた。
１１×１１＝１２１ ・・・ １１（トイ）に１１（トイ）重ねて、１２１（イチニイチ）
１２×１２＝１４４ ・・・ 人に、人に、お人好し
１３×１３＝１６９ ・・・ 意味重ねて重ロック
１４×１４＝１９６ ・・・ いよいよ一苦労
１５×１５＝２２５ ・・・ 一個一個は不都合
１６×１６＝２５６ ・・・ いろいろニコリ
１７×１７＝２８９ ・・・ いいないいなに妬く
１８×１８＝３２４ ・・・ いやいや、ミニよ
１９×１９＝３６１ ・・・ トックリ重ねて寒い
１４×１４＝１９６ を知っていれば、１５×１３＝（１４＋１）（１４−１）＝１９６−１＝１９５ と
簡単に求められる。
（追記） 平成１９年５月６日付け
５月５日、何とはなしにＴＶを見ていたら、インドの九九の話題が取り上げられていた。
例えば、１４×１９ の計算を上述の速算術を用いて、
（１４＋９）×１０＋４×９＝２３０＋３６＝２６６
と説明されていた。（ただ、原理の説明に四苦八苦していたような．．．。）
（参考：日本テレビ系 ウェークアップぷらす ５日（土） ８時〜９時２５分）
追記） 令和４年１２月１１日付け
上記の「１４×１９＝（１４＋９）×１０＋４×９＝２３０＋３６＝２６６」のような計算は、「お土産
算」と言われる。３７×３４などのように、十の位が同じ２桁同士の掛け算に、有効である。
例 ３７×３４＝（３７＋４）×３０＋７×４＝１２３０＋２８＝１２５８
（計算の原理）
（１０ａ＋ｂ）（１０ａ＋ｃ）＝（１０ａ）2＋（ｂ＋ｃ）・１０ａ＋ｂｃ＝（（１０ａ＋ｂ）＋ｃ）・１０ａ＋ｂｃ
この手法を用いると、インド式九九もスラスラ出来そう．．．。
例 １６×１８＝（１６＋８）・１０＋６×８＝２４０＋４８＝２８８
暗算でこの計算をするには、まず「６×８」を計算し、それに「１６＋８」を１０倍したものを
加えればよい。
例 １９×１４＝（１９＋４）・１０＋９×４＝２３０＋３６＝２６６
頭の中では、 ３６＋２３０＝２６６ と計算している。
（追記） 平成１９年９月２８日付け
私の大好きな番組「ためしてガッテン」（NHK）の９月２６日放送で、速算術の話題が取り上
げられた。その中で、上記では述べていない次のような計算に心が引かれた。
２６×２４＝６２４ （（２＋１）×２＝６、後は６×４＝２４）
６３×６７＝４２２１ （（６＋１）×６＝４２、後は３×７＝２１）
・・・・・・・・・・・・・・・・・・・
十の位が同じで、一の位の和が１０である２桁同士のかけ算に有効な方法である。
その原理は、
（１０ａ＋ｂ）（１０ａ＋ｃ）＝１００ａ2＋１０ａ（ｂ＋ｃ）＋ｂｃ＝１００ａ（ａ＋１）＋ｃ2
である。 （ ← これは、よく知られた速算術ですね！）
練習問題 ６４×６６ を計算せよ。
７４×３４＝４×４＋（７×３＋４）×１００＝２５１６
同様に、
７６×３６＝２７３６ （７×３＝２１に６を足して２７、後は６×６＝３６）
４２×６２＝２６０４ （４×６＝２４に２を足して２６、後は２×２＝０４）
・・・・・・・・・・・・・・・・・・・
一の位が同じで、十の位の和が１０である２桁同士のかけ算に有効な方法である。
その原理は、
（１０ａ＋ｃ）（１０ｂ＋ｃ）＝１００ａｂ＋１０（ａ＋ｂ）ｃ＋ｃ2＝１００（ａｂ＋ｃ）＋ｃ2
である。 （ ← これは、初見でした！）
練習問題 ７６×３６ を計算せよ。
また、格子掛け算の話題も取り上げられていた。
（番組では、三角マス目計算法として紹介されていた。）
出演されていたインド人のニャンタさんが
このような計算法は学校では教えない、国家機密である
と仰っていた。番組を見ていて、インドの方々の抜群の計算力に圧倒されました！
（追記） ドイツ語では、次のような数詞が使われている。
| 数 | 数 詞 | 読み方 | 数 | 数 詞 | 読み方 | 数 | 数 詞 | 読み方 |
| ０ | ｎｕｌｌ | ヌル | １０ | ｚｅｈｎ | ツェーン | ２０ | ｚｗａｎｚｉｇ | ツヴァンツィッヒ |
| １ | ｅｉｎｓ | アインス | １１ | ｅｌｆ | エルフ | ３０ | ｄｒｅｉβｉｇ | ドライスィッヒ |
| ２ | ｚｗｅｉ | ツヴァイ | １２ | |
ツヴェルフ | ４０ | ｖｉｅｒｚｉｇ | フィアツィッヒ |
| ３ | ｄｒｅｉ | ドライ | １３ | ｄｒｅｉｚｅｈｎ | ドライツェーン | ５０ | |
フュンフツィッヒ |
| ４ | ｖｉｅｒ | フィア | １４ | ｖｉｅｒｚｅｈｎ | フィアツェーン | ６０ | ｓｅｃｈｚｉｇ | ゼヒツィッヒ |
| ５ | |
フュンフ | １５ | |
フュンフツェーン | ７０ | ｓｉｅｂｚｉｇ | ズィープツィッヒ |
| ６ | ｓｅｃｈｓ | ゼクス | １６ | ｓｅｃｈｚｅｈｎ | ゼヒツェーン | ８０ | ａｃｈｔｚｉｇ | アハツィッヒ |
| ７ | ｓｉｅｂｅｎ | ズィーベン | １７ | ｓｉｅｂｚｅｈｎ | ズィープツェーン | ９０ | ｎｅｕｎｚｉｇ | ノインツィッヒ |
| ８ | ａｃｈｔ | アハト | １８ | ａｃｈｔｚｅｈｎ | アハツェーン | １００ | ｈｕｎｄｅｒｔ | フンダート |
| ９ | ｎｅｕｎ | ノイン | １９ | ｎｅｕｎｚｅｈｎ | ノインツェーン |
ドイツ語の数詞は英語と同様な構造になっている。ただ、例えば、「２１」という数は、英語では、
ｔｗｅｎｔｙ-ｏｎｅ
と上位の位から読んで簡明なのに対して、ドイツ語では、「１＋２０」、つまり、
ｅｉｎｕｎｄｚｗａｎｚｉｇ
と表現され、多少分かりにくい印象を受ける。１００、２００、３００、・・・ などは、日本語に近い。
たとえば、 ３００ ＝ ｄｒｅｉｈｕｎｄｅｒｔ
しかし、一般にドイツ語で数字を読む場合、私など、ほぼ「目がテン！」になってしまう。
４６８ ＝ ｖｉｅｒｈｕｎｄｅｒｔａｃｈｔｕｎｄｓｅｃｈｚｉｇ
（フィアフンダートアハトウントゼヒツィッヒ）
（ここは、やっぱり、「よんひゃく ろくじゅう はち」と読みたいですね！）
さらに、日本では、桁数の多い数に対しては、３桁おきに、「カンマ」を打って、読みやすくする
のに対して、ドイツでは、「カンマ」は小数点を意味することから、日本のようなことはせず、わ
ずかに数字と数字の隙間を僅かに離して、読みにくい点を克服しているようである。
４ ３８２ ＝ ｖｉｅｒｔａｕｓｅｎｄｄｒｅｉｈｕｎｄｅｒｔｚｗｅｉｕｎｄａｃｈｔｚｉｇ
また、ドイツ語には、「万」という単位がないので、
１０ ０００ ＝ ｚｅｈｎｔａｕｓｅｎｄ
と表現しなければならないという難点もある。
このように、ドイツ語の数字の読みにくさから、日本の「九九」のような覚え方があるとは期
待できない。しかも、ドイツ語では、乗算の「×」、除算の「÷」の記号は用いないらしい。
２・４＝８ は、 Ｚｗｅｉｍａｌ ｖｉｅｒ ｉｓｔ ａｃｈｔ．（２ 倍の
４ は ８ である）
１８：３＝６ は、
Ａｃｈｔｚｅｈｎ ｄｕｒｃｈ ｄｒｅｉ ｉｓｔ ｓｅｃｈｓ．（３ によって分たれた
１８ は ６ である）
フランス語は、ドイツ語以上にすごいようだ。たとえば、「８１」などは、「２０ × ４ ＋ １」
と読むので、フランス語にも、日本の「九九」のような覚え方など、到底期待できない。
以上の観点からみると、日本語においては、十、百、千、万、・・・などの位を用いて、数字の
読み方を易しくしているところが、ほかの言語と違う点である。奈良時代から使われ始めたと
される日本の「九九」は、その後も不動の地位を占め、小学校教育の根幹として、現在に至っ
ている。日本の小学生の計算力が優れているのは、まさしく「九九」の覚えやすさにあると思う。
このページは、全く私の独断と偏見で書かれているので、ドイツ語・フランス語に詳しい方で
「これは、違うぞ！」という点がありましたら、こちらにメールをお願いします。
（参考文献：藤原正彦 著 父の威厳 数学者の意地（新潮文庫）
藤田五郎 著 現代ドイツ文典（郁文堂）
田島 宏 著 初歩のフランス語（昇龍堂））
（追記） 当ＨＰの読者の方から、数字の区切りについて、ご意見を頂いた。貴重なご意見に
感謝いたします。（平成１７年４月２３日付け）
上記で、「日本では、桁数の多い数に対しては、３桁おきに、「カンマ」を打って、読みやす
くする」と書いたが、この流儀は、もともとは英語圏の発想とのことである。たしかに、英語圏
では thousand、million、billion、trillion（米）というように３桁ずつ数詞が変わるので、
２５７８６５４２３５８４５６ を、２５trillion７８６billion５４２million３５８thousand４５６ と読むと
ころを、２５，７８６，５４２，３５８，４５６ と表記するのはとても合理的に感じる。
日本ではむしろ４桁おきに、「カンマ」を打った方が読みやすいかもしれない。
２５７８６５４２３５８４５６ を、２５兆７８６５億４２３５万８４５６ と読まなければならないが、
２５，７８６５，４２３５，８４５６ と区切られていると、右側から、万、億、兆で読みやすい。
私が小学生の頃は、このように４桁ずつ区切るように教わった覚えがあるのだが、いつし
か３桁ずつ区切ることに慣らされてしまった。
（追々記） 平成２０年６月８日付け
朝日新聞 ７日付け夕刊で、「九九の秘密を探れ」という記事が目に止まった。
杉並区立高井戸第三小学校の吉田映子さんの授業実践報告である。
下図のような「九九ジオボード」を用意して、「０」から順次、九九の掛け算で答えの一の位
の数字に紐をかけていく。
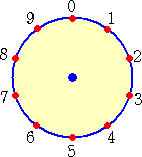
そうすると、同じような文様になるものが出来るという。面白そうなので、実際にやってみた。
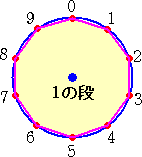
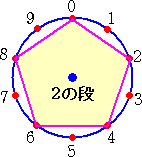
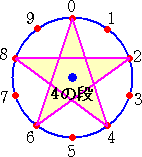
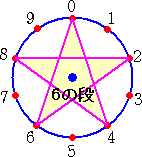
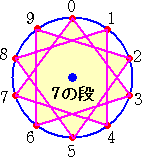
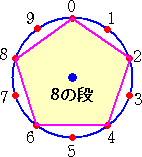
上図から、１の段と９の段、２の段と８の段、３の段と７の段、４の段と６の段 が同じ
文様になる。 今までこのようなことをしたことがなかったので、とても新鮮だ！
上記の性質を一般化すれば、
一桁の自然数 ｎ に対して、 ｎ の段と １０−ｎ の段 は同じ文様になる
（証明） 自然数 ｋ （１≦ｋ≦９）に対して、
ｎ・ｋ＋（１０−ｎ）・ｋ＝１０ｋ≡０ （ｍｏｄ １０）
よって、 ｎ の段の一位の数と １０−ｎ の段の一位の数は足すと必ず
１０ になる。
したがって、ｎ の段の一位の数と １０−ｎ の段の一位の数それぞれの取り得る値
は一致する。 （証終）
