図形を用いて求めた人がいる。古代インドの「シュルバスートラ」という文献で述べられている。
「一夜一夜に人見頃」という覚え歌は有名で、1.41421356・・・ という値は、中学で教え
られる。この値にはちょっとおよばないが、1.41421・・・ という値を、古代インドの人々が知
っていたということを知り、とても感動した。
縦が1、横が2 の長方形を考え、下記のように、いくつかの長方形に分割する。
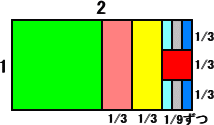
この小長方形を組み合わせて、下図のように正方形の中に配置する。

・ 平方根2の近似値 S.H氏
![]() が分数で表せないことは、古代ギリシアのピタゴラス学派により発見されたが、その値を
が分数で表せないことは、古代ギリシアのピタゴラス学派により発見されたが、その値を
図形を用いて求めた人がいる。古代インドの「シュルバスートラ」という文献で述べられている。
「一夜一夜に人見頃」という覚え歌は有名で、1.41421356・・・ という値は、中学で教え
られる。この値にはちょっとおよばないが、1.41421・・・ という値を、古代インドの人々が知
っていたということを知り、とても感動した。
縦が1、横が2 の長方形を考え、下記のように、いくつかの長方形に分割する。

この小長方形を組み合わせて、下図のように正方形の中に配置する。

| この図を用いると、1辺の長さが |
| の正方形よりも大きく、1辺の長さが | の正方形より小さいことが分かる。 |
したがって、
| < |
|
文献では、 |
ということが述べられているそうだ。 |
右辺の値を、小数展開すれば、1.414215686・・・ となる。電卓がない時代に、小数点以
下第5位まで正しく求めていたという事実に驚きを隠せない。
平方根2 の話題について、もっと知りたい方は、下記をご参照下さい。
平方根2 を求める数列 平方根・立方根を筆算で求める方法
(追記) 「シュルバスートラ」という文献は、古代インドにおいて、バラモン教の祭祀を厳格に
行うため、いろいろな規定に基づいて祭壇の位置や形状を決める作図法を記したもの
である。正方形の対角線の長さと 1辺の長さの比のことを、「サヴィシェーシャ」と呼び、
近似値として、分数をあてたとのことである。平方根2としては、577/408 となる。
(追々記) 平方根2を表す分数として、上記では、577/408 をあげたが、実は、この分数
( → 577/408 = 1.4142156・・・ )より精度がいい分数を、機械的に作るこ
とは可能で、その方法は、「平方根2 を求める数列」で述べられている。
このページでは、もう少し分かりやすい求め方を紹介しよう。
分子・分母の桁数の比較的小さい分数で、平方根2に最も近い分数としては、例えば、
3363/2378
があげられる。小数に直せば、何と 1.4142136・・・ である。
この分数は、( a/b → (a+2b)/(a+b) )という手順を繰り返すことにより得られる。
実際に、 1/1 → 3/2 → 7/5 → 17/12 → 41/29 → 99/70
→ 239/169
→ 577/408 → 1393/985 → 3363/2378
である。
実は、( a/b → (a+nb)/(a+b) )という手順を繰り返すことにより、平方根 n に収
束する数列が作られる。
(求め方は、Xk+1=Xk+nYk 、Yk+1=Xk+Yk を解けばよい。
(→参考:平方根2 を求める数列))
(参考文献:ブライアン・ボルト 著 木村良夫 訳 数学パズル・パンドラの箱(講談社))
