Ｆ2（ｘ，ｙ，ｚ）＝ｘ＋ｙ2＋ｚ−１＝０ ・・・ （２）
Ｆ3（ｘ，ｙ，ｚ）＝ｘ＋ｙ＋ｚ2−１＝０ ・・・ （３）
連立方程式を可視化すると、右図のようになる。
（少し分かりにくいかな？想像をふくらませてください。）
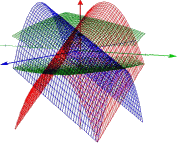
・連立方程式 Ｓ．Ｈ 氏
大阪大学の日比孝之先生が、数学セミナー（’１２年２月号）で次の連立方程式を題材に
グレブナー基底を説明されている。
| Ｆ1（ｘ，ｙ，ｚ）＝ｘ2＋ｙ＋ｚ−１＝０ ・・・ （１） Ｆ2（ｘ，ｙ，ｚ）＝ｘ＋ｙ2＋ｚ−１＝０ ・・・ （２） Ｆ3（ｘ，ｙ，ｚ）＝ｘ＋ｙ＋ｚ2−１＝０ ・・・ （３） 連立方程式を可視化すると、右図のようになる。 （少し分かりにくいかな？想像をふくらませてください。） |
|
日比先生によれば、受験数学の常套手段を用いると、この連立方程式は、
Ｇ1（ｘ，ｙ，ｚ）＝ｘ＋ｙ＋ｚ2−１＝０
Ｇ2（ｘ，ｙ，ｚ）＝ｙｚ2＋（ｚ4−ｚ2）/２＝０
Ｇ3（ｘ，ｙ，ｚ）＝ｙ2−ｙ−ｚ2＋ｚ＝０
Ｇ4（ｘ，ｙ，ｚ）＝ｚ6−４ｚ4＋４ｚ3−ｚ2＝０
と変形されるとのことであるが、その式変形が悩ましい．．．。
｛Ｇ1，Ｇ2，Ｇ3，Ｇ4｝が、｛Ｆ1，Ｆ2，Ｆ3｝のグレブナー基底となるらしい。
連立方程式を解くだけだったら簡単だ。次のように解けばよい。
（解） （１）−（２） より、 （ｘ−ｙ）（ｘ＋ｙ−１）＝０ なので、 ｘ＝ｙ または ｘ＋ｙ＝１
ｘ＝ｙ のとき、（２）（３）に代入して、 ｙ＋ｙ2＋ｚ−１＝０ 、 ２ｙ＋ｚ2−１＝０
ｚ＝１−ｙ−ｙ2 を、２ｙ＋ｚ2−１＝０ に代入して整理すると、 ｙ4＋２ｙ3−ｙ2＝０
よって、 ｙ2（ｙ2＋２ｙ−１）＝０ より、 ｙ＝０、−１±
ｙ＝０ のとき、 ｚ＝１
ｙ＝−１± のとき、 ｚ＝１−ｙ−ｙ2＝−１± （複号同順）
ｘ＋ｙ＝１ のとき、 （３）より、 ｚ2＝０ なので、 ｚ＝０
このとき、 ｘ2＋ｙ−１＝０ で、 ｙ＝１−ｘ を代入して整理すると、 ｘ2−ｘ＝０
よって、 ｘ＝０ 、 １
ｘ＝０ のとき、 ｙ＝１
ｘ＝１ のとき、 ｙ＝０
以上から、求める連立方程式の解は、
（ｘ，ｙ，ｚ）＝（０，１，０）、（１，０，０）、（０，０，１）、
（−１±，−１±，−１±） （複号同順）
空舟さんからのコメントです。（平成２４年２月２１日付け）
連立方程式
Ｆ1（ｘ，ｙ，ｚ）＝ｘ2＋ｙ＋ｚ−１＝０ ・・・ （１）
Ｆ2（ｘ，ｙ，ｚ）＝ｘ＋ｙ2＋ｚ−１＝０ ・・・ （２）
Ｆ3（ｘ，ｙ，ｚ）＝ｘ＋ｙ＋ｚ2−１＝０ ・・・ （３）
について、「放物線の交点」を参考にして、立体座標幾何的に考えてみました。
(1)+(2)+(3)=0 を考えると、 ｘ2+ｙ2+ｚ2+2ｘ+2ｙ+2ｚ-3=0 を得る。
(ｘ+1)2+(ｙ+1)2+(ｚ+1)2=6 ・・・ (-1，-1，-1) を中心とする半径
の球面Sである。
(1)-(2)、(2)-(3)を連立すると、[(1)=(2)=(3)ということ]
(ｘ-ｙ)(ｘ+ｙ-1)=0 、 (ｙ-ｚ)(ｙ+ｚ-1)=0
グラフを考えると、２つの"＋柱"の交わりで、４本の直線からなります。
直線 ｘ=ｙ=ｚ 、点(-1，0，0)を通る(-1，1，1)向きの直線、
点(0，-1，0)を通る(1，-1，1)向きの直線、点(0，0，-1)を通る(1，1，-1)向きの直線
・・・ まとめると、点(1/2，1/2，1/2)を通る４つの直線
これらの直線と球面Sとの交点が求める解になります。
一般の球と直線の交点を考察する方法を一応書いておきます。
球の中心をA、直線上の有る点をB、直線ベクトルを ｐ とします。垂線の足Ｈは、
H=B+{(A-B)・ｐ/|ｐ|}ｐ
と得ます。(いわゆるシュミットの方法の一部と言えます。)
そうすれば、直線と球の中心の距離が分かります。あとは、三平方の定理で垂線の足か
らの距離を求めればよいです。
今回では、直線 ｘ=ｙ=ｚ は、球の中心を通るのは自明ですが、その他の３本の直線は球
の中心との距離がで、球面Sに接していることが分かりました。
[その接点が、(1，0，0)、(0，1，0)、(0，0，1)]
Ｓ（Ｈ）さんからのコメントです。（平成２４年２月２３日付け）
参考→講義（動画）
n = 2 のとき、 I2={ｘn + ｙ + ｚ - 1， ｘ + ｙn + ｚ - 1， ｘ + ｙ + ｚn - 1}={0，0，0}
n = 3 のとき、 I3={ｘn + ｙ + ｚ - 1， ｘ + ｙn + ｚ - 1， ｘ + ｙ + ｚn - 1}={0，0，0}
n = 4 のとき、 I4={ｘn + ｙ + ｚ - 1， ｘ + ｙn + ｚ - 1， ｘ + ｙ + ｚn - 1}={0，0，0}
.
.と、カルビー型の問題に。「数学セミナー グレブナー基底」絡みの濃厚な話題の導入問題
らしい........。K[ｘ，ｙ，ｚ]/In の考察でどうにも.....。
