2つの放物線 y=−x2+x+1 、x=y2+y−1 の交点を求めることは大変そう..カナ?
実際に、 2式を辺々加えて、 x+y=−x2+y2+x+y より、 x+y=0 、 x−y=0
x+y=0 のとき、 y=−x を y=−x2+x+1 に代入して、 x2−2x−1=0
よって、 x=1±
したがって、 ( x , y )=( 1+
x−y=0 のとき、 y=x を y=−x2+x+1 に代入して、 x2=1 より、 x=±1
したがって、 ( x , y )=( 1 , 1 ) 、( −1 , −1 )
もっとも上記のような計算をしなくても、交点がどのように分布しているかはグラフにより
視覚的に捉えることができる。

さらに、上の「4交点が、実は同一円周上に分布している」ということを聞くと、驚かれる
方がおられるかもしれない。
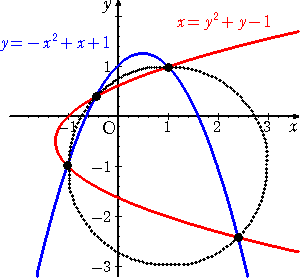
上の円の方程式は、次のようにして得られる。
2つの放物線の方程式 y=−x2+x+1 、x=y2+y−1 より、
x2−x+y−1=0
y2−x+y−1=0
これらを辺々加えて、 x2+y2−2x+2y−2=0 となる。
すなわち、 (x−1)2+(y+1)2=4 より、 中心(1,−1)で半径2の円
である。
さらに、この4点を通る図形は、もちろん一意に定まることはなく、自由自在に作ることが
できる。
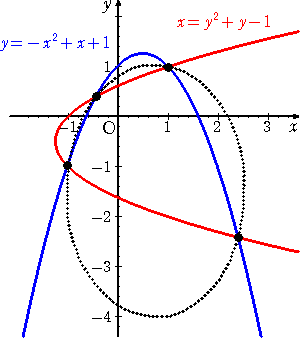
左図は、4点を通る楕円である。
方程式は、
2x2+y2−3x+3y−3=0 である。
この方程式は、
x2−x+y−1=0 の両辺を2倍し、
y2−x+y−1=0 に辺々加えること
により得られる。
同様にして、 x2−x+y−1=0 、y2−x+y−1=0 を適宜加減すれば、下図のような、
4点を通る双曲線も得られる。
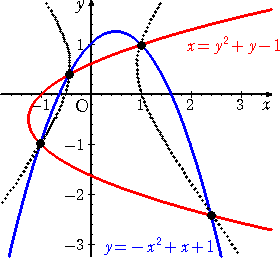
左図の方程式は、
2x2−y2−x+y−1=0
である。
(追記) 平成26年3月2日付け
上記で、放物線 y=−x2+x+1 と円 x2+y2−2x+2y−2=0 は4点で交わり、その交
点は、
A( 1+
である。このとき、
直線ABの傾きは、−1で、直線CDの傾きは、1 なので、
円と放物線の4交点をA、B、C、Dとするとき、(直線ABの傾き)+(直線CDの傾き)=0
という関係が成り立ちそうだ。この予想は正しく、次のようにして確かめられる。
(証明) 回転移動と平行移動を施すことにより、
円の方程式 : x2+y2=r2 放物線の方程式 : y=ax2+bx+c
としても一般性は失われない。代入して整理すると、
a2x4+2abx3+(b2+2ca+1)x2+2bcx+c2−r2=0
4つの交点のx座標をα、β、γ、δとすると、解と係数の関係より、
α+β+γ+δ=−2b/a
このとき、 (直線ABの傾き)+(直線CDの傾き)
=a(α+β)+b+a(γ+δ)+b=a(α+β+γ+δ)+2b=0 (証終)
(コメント) この定理は、らすかるさんよりご教示頂きました。美しい関係ですね!
らすかるさんに感謝します。
