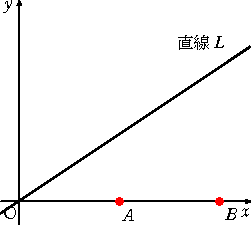
座標平面上の2点A(1,0)、B(2,0)を考える。
原点Oを通る直線 L は座標軸には重ならないよ
うに動くものとする。
・ 絶妙な点の配置 S.H氏
 |
座標平面上の2点A(1,0)、B(2,0)を考える。 原点Oを通る直線 L は座標軸には重ならないよ うに動くものとする。 |
| 直線 L に関して点Bと対称な点をCとし、 線分ACと直線 L の交点をDとする。 |
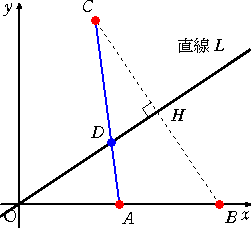 |
このとき、直線 L がどのように動いても、CD : DA は一定であることを示せ。
上記の問題設定で、直線 L
が動くことは全くのまやかしである。
この問題に対する解答は種々考えられて、とても面白い。
(1) 角の2等分の性質を利用するもの
上図から角の2等分を思いつく方はそんなにいないことと思う。
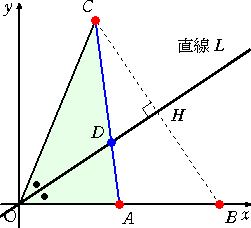 |
左図の△OABにおいて、 OC=OB=2OA である。 線分ODは∠AOCの2等分線であるので、 CD : DA=OC : OA=2 : 1 が成り立つ。 |
(2) 中点連結の定理を利用するもの
私が最初に思いついた解法。息子からは、「よくそんな発想が浮かぶね!」と言われて
しまった。そんなに突拍子もなく、ごく自然な解法だと思うのだが...。
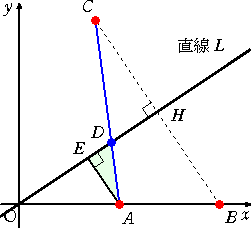 |
直線 L
に点Aより垂線の足Eを下ろす。 このとき、中点連結の定理より、 AEとBHは平行で、 BH=2AE が成り立つ。 また、△CDH∽△ADE なので、 CD : DA=CH : AE=BH : AE=2 : 1 が成り立つ。 |
(3) 重心の性質を利用するもの
この解法が最も簡単で、感動的ですらある...。
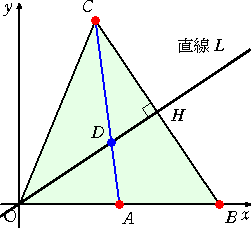 |
点Dは、△OBCの重心なので、 CD : DA=2 : 1 である。 |
(4) メネラウスの定理を利用するもの
(3)の解法を見せられると、とても恥ずかしくて表に出せないような...予感。
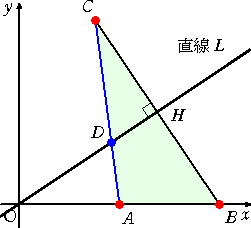 |
左図の△ABCにおいて、 メネラウスの定理より、 なので、 CD=2DA が成り立つ。 すなわち、 CD : DA=2 : 1 である。 |
もしかしたら、上記以外にももっと別な求め方があるかも知れない。何か問題作成の宝庫
となりそうな...そんな雰囲気である。
別解を考えられた方は、是非こちらにお教え下さい。
(追記) 平成20年10月26日付け
当HPの掲示板「出会いの泉」に、10月24日付けで、S(H)様が上記の問題の一般化に
ついて書き込みをされた。S(H)様に感謝します。
OA = s 、AB = t とすると、 CD : DA = s+t : s が成り立つことを、実際に、点C、
Dの座標を計算することによって示されている。
上記の(4)におけるメネラウスの定理を活用すれば、CD : DA = s+t
: s が成り立つ
ことは明らかなわけであるが、私自身、正直に告白すると、当初この問題を考えたときに、
強引にCの座標、Dの座標を計算して線分の比を求めようとして、あまりの計算の煩雑さに
嫌気がさして途中で計算を打ち切り、挫折した経験がある。
ここでは、S(H)様の計算を参考にしながら、再度、その計算に挑戦してみようと思う。
原点を通る直線 L の方程式は、一般的には、 ax+by=0 で与えられるが、題意より、
座標軸と重なることはないので、ここでは、 y=mx を考えれば十分である。
直線 y=mx に関する対称移動は一次変換で、行列
![]()
で表される。よって、点B( s+t , 0 )の直線 L に関する対称点Cの座標は、
![]()
となる。この点Cと、点A( s , 0 )を通る直線の方程式は、
![]()
なので、点Dの x 座標は、
![]()
となる。
このとき、
![]()
![]()
から、 CD : DA = s+t : s であることが分かる。
上記の計算では一次変換を利用したが、S(H)様は、ベクトルを利用して計算されたよう
である。
実際に、 直線 y=mx の法線ベクトルは、 ( m , −1 ) なので、点Bを通り、直線
L
に垂直な直線のベクトル方程式は、 ( x , y )=( s+t , 0 )+k(
m , −1 ) となる。
x=s+t+km 、 y=−k を、 y=mx に代入して、
![]()
が得られるので、 ( x , y )=( s+t , 0 )+2k0( m , −1 ) より、点Cの座標は、
![]()
となる。以下は、多分上記と同様の計算だろう。
(コメント) 私が途中で計算を打ち切った原因は、計算方針(CD、DAの計算)に誤りがあ
ったようです。
(追記) 平成20年10月27日付け
26日付けのS(H)様からの情報によると、
直線 L を y=mx とする.とき、点Dの軌跡を考察する
という問題もあり得るという。
このとき、直線 L は、2点A、Bを焦点とする楕円に接し、点Dは接点になる。
このことは、下図において、焦点Aを発した光線が点Dで反射して、他の焦点Bに達する
という事実から理解されるだろう。(→ 参考:「楕円」)
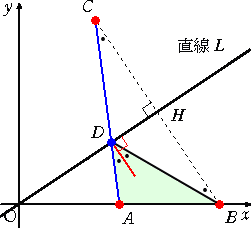
点Dの軌跡自体は、2定点A、Bからの距離の比が等しいので、線分ABを、 s+t : s に
内分、外分する点を直径の両端とする円(アポロニウスの円)となる。但し、軌跡から
x 軸と
の交点は除かれる。
また、S(H)様からの情報によると、この問題は、
定点A(1,0)、B(2,0)とし、直線 y=mx (m≠0)にy=mx(m≠0)を
L とする。
また、直線 L 上に点Dを、AD+BD が最小になるようにとる。このとき、m
の変化に
よって、点Dはどのような図形を描くか。
とも言い直せるとのこと。こういう状況では、直線 L に関して、点Bと対称な点Cを考えるこ
とは、受験テクニックに限らず当然の対応ですね!
(追記) 平成20年10月29日付け
26日付けで、S(H)様から次のような問題と、その解答の指針が提示された。
A(1,0)、B(2,0)を焦点とし、直線 y=mx に接する楕円Emの接点Dの軌跡を
求めよ。
この問題を、次の手法で考察せよ。
A(1,0)、B(2,0)を焦点とする楕円を ![]() とし、
とし、
この楕円と直線 y=mx について、次の問いに答えよ。
(1) 唯一の交点をもつように関数 K=G(m) を定めよ。
(2) x 、y の連立方程式 ![]() 、 y=mx を解
、 y=mx を解
き、 x=fx(m)、y=fy(m) となる関数 fx、fy を定めよ。
(3) 上から mを消去せよ。特に、【シルベスター行列を用いる発想】は必ず実行せよ。
(4) mを消去して得られた F(x ,y)=0 から x 軸との交点を除外したものが、軌跡で
ある。
(5) F(x ,y)=0 は 2超平面 : 4 −3x − 3my =0 、 −mx +y =0 からも得
られる。これを示せ。
(6) 4 −3x − 3my =0 、 −mx +y =0 の成り立ちを述べよ。
(追伸) 楕円族 : ![]() において許容されるKの範囲
において許容されるKの範囲
を求めよ。
平面上の2点A( 1 , 0 )、B( 2 , 0 )を焦点とする楕円に、原点を通る直線L
: y=mx
が接するとき、楕円の方程式は、m
を用いてどう書けるだろうか。
興味ある問題なので、計算してみた。対称性から、m>0 として考えることにする。
楕円の中心は、点( 3/2 , 0 )なので、全体を x 軸方向に −3/2 だけ平行移動して考
える。 このとき、O’( −3/2 , 0 )、A’( −1/2 , 0 )、B’(
1/2, 0 ) となる。
求める楕円の長軸の長さを K(=2a)とすると、楕円の方程式は、
![]()
と書ける。ただし、4a2−4b2=1 である。
この楕円の補助円の方程式は、 x2+y2=a2 である。
点O’( −3/2 , 0 )を通る直線が、円 x2+y2=a2 に接するとき、その接点の座標
( x1 , y1 )は、連立方程式 (−3/2)x1=a2 、 x12+y12=a2 を解くことにより得られ
る。実際に解くと、
![]()
である。この点を y 軸方向に b/a
倍した点が、直線 L と楕円との接点となる。すなわち、
![]()
(→ 参考:「楕円の接線」)
このとき、直線 L の傾き m について、
![]()
となる。これを a について解き直せば、
![]()
となる。このとき、
![]()
このことから、m の値が分かれば楕円の方程式は確定する。
例えば、m=1 に対して、その楕円を求めて図示すると下図のようになる。
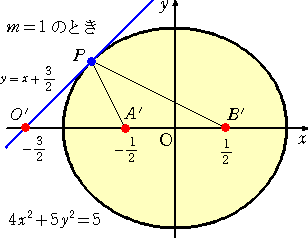
接点 P の座標も m の関数として表される。実際に、上記の結果から、
![]()
となる。
また、直線 L : y=mx に接する楕円上の点と2つの焦点からの距離の和
K の値は、
![]()
で与えられる。これはS(H)様の解答の指針(1)の答えである。
(コメント) 横方向に平行移動しなくてもよかったような...予感。
また、上記の点Pを x 軸方向に3/2だけ平行移動させれば、S(H)様の解答の指針(2)
の答えが得られる。
![]()
これより、m を消去する手順は、軌跡の計算では定石的な方法であろう。
実際に、 m=y/x を代入して整理すると、円の方程式
x2+y2−(4/3)x=0
が得られる。ただし、求める軌跡からは、2点( 0 , 0 )、B( 4/3 ,
0 )は除かれる。これ
はS(H)様の解答の指針(3)(4)の答えである。
上記では、文字 m を消去するのに受験テクニックを用いたが、正統的な消去法(シルベ
スターの消去法)を用いるとすれば、次のように計算される。
![]()
より、 3xm2+3x−4=0、3ym2−4m+3y=0 なので、
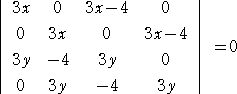
が成り立つ。
この行列式を計算すれば、円の方程式 x2+y2−(4/3)x=0 が得られる。
また、連立方程式 3xm2+3x−4=0 、3ym2−4m+3y=0 において、後者は前者と
y=mx から得られるので、連立方程式 3xm2+3x−4=0 、y=mx を考えてもよい。
すなわち、連立方程式 3my+3x−4=0 、y=mx から
m
を消去しても、円の方程式
x2+y2−(4/3)x=0 が得られる。これは、S(H)様の解答の指針(5)の答えである。
問題は、S(H)様の解答の指針(6)である。具体的に接点を求めてしまえば、
3my+3x−4=0
という式は出現するのだが、それでは多分S(H)様の意図することと違うことになってしまう
ことだろう。 多分、図形的に追究してみると解決しそうな...予感!
点Dは△OBCの重心なので、CD
: DA=2 : 1 であった。さらに、直線L
に垂直で点D
を通る直線は、∠ADBの2等分線となる。しかも、△DBCは、DB=DCの2等辺三角形な
ので、DA : DB=1 : 2 となる。角の2等分線の性質より、∠ADBの2等分線と
x 軸と
の交点の座標は、m の値によらず一定で、点(4/3 ,0)である。(← 美しすぎる!)
よって、∠ADBの2等分線の方程式は、
y=(−1/m)(x−4/3) すなわち 3my+3x−4=0
となる。この直線の方程式は、点Dの座標が分からなくても求められるところが素晴らしい。
しかも、y=mx と連立すれば、点Dの軌跡の方程式が簡単に求められる。
(コメント) このような問題は以前より見慣れたものの筈だったが、S(H)様から頂いた解答
の指針に従って考えてみると、これまで抱いていた感覚とは違う新鮮な息吹を感じざ
るを得ない。このような機会を与えて頂いたS(H)様に感謝いたします。
S(H)様の(追伸)の問題 :
![]()
の取り得る値の範囲を求めることも容易だろう。簡単な計算から、 1<K<3 であること
が分かる。
