・　正八面体に親しむ 　　 　 　　　　 　　　　　　　Ｓ．Ｈ氏

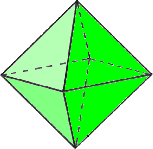　　　　正８面体というと、左図のような立体図形を想起される方が
　　 大多数だろう。

　　　平成２０年度の東京大学　前期　理系の問題３に、

　　　　正八面体のひとつの面を下にして水平な台の上に置く。
　　　この正八面体を真上から見た図（平面図）を描け。

　　という問題が出題された。

　空間把握に弱点を持つ現役の高校生にとっては難問に映ったろう。普段から、このような
立体図形に親しんでいる方にとって何でもない問題なのだが、採点が大変そうな．．．予感。
多分、図を書けば満点に近い点数を貰えるのかな？

　各予備校の分析も「やや難」ということで、数学がポイントゲッターの人にとっては厳しい春
となりそうだ。

　このような問題は、随分昔に出題された「立方体の平面への投影」以来かな？

　下図のようにイメージ出来れば、何とか正解にはたどり着けるだろう。

　　　　　　　　　　　

　正解図は、２つの正３角形の重心が重なった下図の正６角形となる。

　　　　　　　　　　　

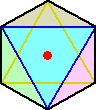
　上図のようになることを言葉で説明することは、少し悩ましいかな？

（追記）　平成２０年４月７日付け

　正八面体の１辺の長さを、ａ とすると、その体積は、

　　　　　　　　

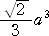
で与えられる。（→　参考：「正多面体が５種類しかない理由」　）

　　　これは、正方形の対角線の長さの半分が、ａ/　なので、

ａ2×（ａ/）×（１/３）×２＝

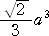　　と簡単に求められる。



　東京大学の問題風に正八面体という図形をとらえるとき、体積の計算には不向きであろ
うと思われたが、次のような見方をすると容易であることを、当ＨＰがいつもお世話になって
いるｚｋ４３さんにご教示いただいた。ｚｋ４３さんに感謝いたします。


　　　左図の立体図形の側面に３個、上部に１個の、何れも１辺の長さが ａ
　　の正四面体を追加して貼り合わせると、１辺の長さが ２ａ の正四面体が
　　１個できる。



　　　　　　　　　　　　　　　

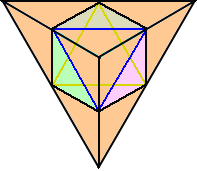
　したがって、１辺の長さが ａ の正八面体の体積を Ｖ、１辺の長さが ａ の正四面体の体積
を Ｗ とおくと、

　　　Ｖ＋４Ｗ＝８Ｗ　　（←右辺は、相似比の性質「体積比は相似比の３乗に比例」より）

より、　　Ｖ＝４Ｗ　　が成り立つ。

　数学�Tで学ぶ公式　　Ｗ＝（/１２）ａ³　　を用いれば、体積 Ｖ は明らかに、

　　　　　　　

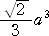
で与えられる。

　（このＷの公式を導くのに、教科書では１ページを割いているくらい大変です。ｚｋ４３さんも指摘してい
　るように、Ｖ＝４Ｗ の関係を知っていれば、Ｖ を求めることは上記で見たとおり易しいので、直ぐにＷ
　が求められますね！これって、裏技．．．かも？）

（コメント）　上図のように正四面体を補充すると、また正四面体ができるなんて美しすぎま
　　　　　　すね！このような見方が可能ということを知ったら、やはり東京大学の問題には
　　　　　　深遠なる趣がヒシヒシと伝わってくるような気高さを感じます。

　東京大学の問題の視点で、次のような問題が想起される。

　上面の正三角形と底面の正三角形の幅は如何ほどだろうか？

　この問題は、三平方の定理を活用すれば直ちに求められる。

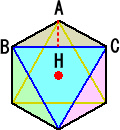左図において、Ｈは正三角形の１辺ＢＣの中点である。 　　このとき、Ｈより底面に下ろした垂線の足とＡを結ぶ線分の長さは、 　　　（/２）ａ×（１/３）＝（/６）ａ　である。 　　この長さの２倍、すなわち、　（/３）ａ　が左図の正六角形の 　１辺の長さとなる。

　以上から、２つの面の幅は、
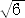　　　　　　　　　　　　　　　　　　　　（/３）ａ

で与えられる。

　読者のために、練習問題を残しておこう。


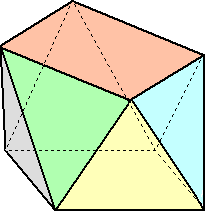
　　　上面と底面が正方形で、側面が正三角形の立体
　　図形を考える。正方形の１辺の長さを ａ として、上
　　面の正三角形と底面の正三角形の幅を求めよ。

答えは、

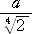となる。できたかな？