簡単な説明・証明が知りたいです。よろしくお願いします。
(コメント) 参考 → 立方体の展開図
りらひいさんからのコメントです。(令和5年10月16日付け)
あっているかはわかりませんが、たぶんこうかなぁと思うものを書きます。違っていたらごめ
んなさい。
正六面体と正八面体は双対の関係なので、隣り合う面の中心同士を結ぶと相手の立体に
なります。
このとき、面が頂点に置き換わり、辺が辺に置き換わり、頂点が面に置き換わります。
図を見てください。

左が正六面体の展開図で、右がそれに対応する正八面体の展開図です。
この図における対応関係の例を挙げると、
正六面体の面ABCD ⇔ 正八面体の頂点P
正六面体の辺AB ⇔ 正八面体の辺PQ
正六面体の頂点A ⇔ 正八面体の面PQR
などになります。(辺は交差しているものが対応していると考えればよいです。)
この図を見てみると、次のようなことがわかります。
正六面体展開図で面が切り離されている辺と正八面体展開図で面がつなげられている辺
が対応しており(例えばABとPQ)、正六面体展開図で面がつなげられている辺と正八面体展
開図で面が切り離されている辺が対応している(例えばAEとQR)。
図は、この法則を利用して作りました。
一方の展開図を書いておいて、もう一方はこの法則に従って、面をつなげていけば出来上
がります。
ほかの展開図でも、同じ法則で対応する展開図が描けるかは未確認です。もし間違って
いたらこの投稿はスルーしてください。
(コメント) 正六面体と正八面体の関係をまとめてみました。

(参考) 「正多面体が5種類しかない理由」
(コメント) 正六面体の(頂点数,辺数,面数)が、(8,12,6)であるのに対して、正八面体
のそれは、(6,12,8)であるので、 頂点 ⇔ 面 、辺 ⇔ 辺 、面 ⇔ 頂点 の対応で
正六面体と正八面体は双対の関係にある。
正六面体の展開図は、次の11通りである。

また、正八面体の展開図は、次の11通りである。
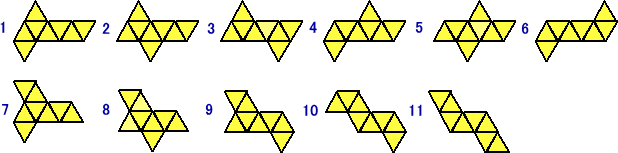
りらひいさんの考察によれば、正六面体の展開図5と正八面体の展開図8が対応すること
になる。
問題 正六面体の展開図2と対応する正八面体の展開図はどれであろうか?
(解) 正六面体の展開図2と対応する正八面体の展開図は、「9」である。
実際に、正六面体の展開図2において、正八面体の対応する頂点を記入すると、

となる。このとき、辺PR、RS、ST、TQ、SUは隣り合う面を結ぶので、正八面体においては、
面としては隣り合わないことになる。次の8枚の正三角形において、赤線を境界線として面が
隣り合うことはない。黒線は、面同士が隣り合うことを表す。
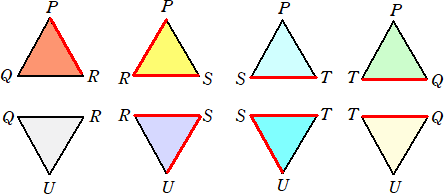
これらを貼り合わせて、下図を得る。

よって、正六面体の展開図2と対応する正八面体の展開図は、「9」である。
貼り合わせの方法(赤線が外枠)から、展開図はただ一つに確定する。
同様に、正六面体の他の展開図が正八面体のどの展開図に対応するのかを調べると、
次の表のように1対1に対応していることが分かる。



