4本の線分を引く。但し、これらの線分は辺に平行にならないものとし、4本の線分で囲まれ
た図形が四角形になる場合を考える。
その四角形の面積が元の正方形の面積の n/m 倍になるようにしたい。
1/2、1/3、1/4、1/5 は作れました。
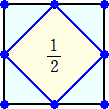


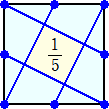
さて、1/6は作れるでしょうか?
(コメント) 次のようにすれば出来ますね。
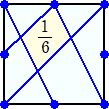
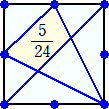
他に、5/24、1/16 の場合も作ってみました。
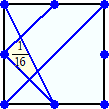
らすかるさんからのコメントです。(令和2年4月20日付け)
正方形ABCDで、AB、BC、CD、DAの中点を、E、F、G、Hとするとき、BD、BH、EF、GHの4
本を引けば出来ますね。
ksさんからのコメントです。(令和2年4月20日付け)
出来ました!1/8、1/12、3/8、3/16 などもできました。少しコツを掴んだので、2/3、1/7 も
挑戦します。
らすかるさんからのコメントです。(令和2年4月21日付け)
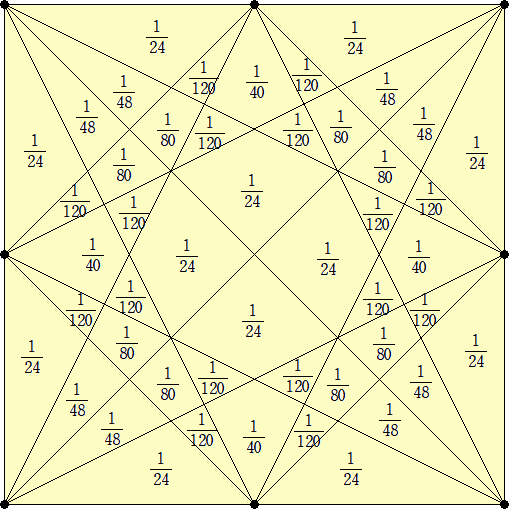
全ての線を引いて細かく分けられた領域の面積を求めると、
1/120 、1/80 、1/48 、1/40 、1/24
の5種類しかなく、120と80と48と40と24の最小公倍数は240ですから、分母が240の約数で
ないものは不可能です。また、別の理由で、2/3も出来ないと思います。
ksさんからのコメントです。(令和2年4月21日付け)
解は複数解ある場合があります。例えば、1/3は、BH、FD、EF、GH
1/4は、EH、BD、EF、GHも可能です。1/5の別解は、未。
(コメント) らすかるさんのように、考えられる線分をすべて引いて面積を求めてみました。
この図とにらめっこすると所要の四角形がどこに作られるか分かるのかな...。
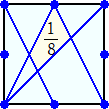
例えば、1/8 は、(1/24)×2+(1/120)×2+1/40=1/8 なので、次の四角形が該当する。
ksさんからのコメントです。(令和2年4月22日付け)
らすかるさんから、2/3が不可能ということで、内分点を増やして挑戦しましたが、五角形に
なったり、対角線でなかったり、うまくいきません。
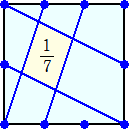
1/n を作りたいときは、n-1=ab のとき、横をa等分、縦をb等分し、対辺と一段ずらして結ぶ
と可能です。1/7、1/9、1/10 などもできました。
例えば、1/7 は、ab=6 より、a=3、b=2として、次の図で与えられます。
(参考) 面積計算2 、面積計算7の(2) 、面積計算8
内分点を自由化すれば、あらゆる分数が可能な気がするのですが?
らすかるさんからのコメントです。(令和2年4月22日付け)
はい、そうなりますね。内分点が任意の整数比ならば、1より小さい任意の有理数面積の
「平行四辺形」が作れますね。
ksさんからのコメントです。(令和2年4月22日付け)
らすかるさん、いつもありがとうございます。
2/3が、8と10等分し、1/81を6×9個で、54/81で可能になりました。分割を少なくしたいで
すが...。
5×13等分し、1/66を44個で、44/66で可能でした。
らすかるさんからのコメントです。(令和2年4月22日付け)
2/3を作るには、半分で1/3を作れればよいので、例えば、
ABを1:4に内分した点とDをつなぐ
BCを4:1に内分した点とDをつなぐ
CDを1:4に内分した点とBをつなぐ
DAを4:1に内分した点とBをつなぐ
のようにすれば、ひし形の面積が2/3になりますね。
ksさんからのコメントです。(令和2年4月22日付け)
何故五分割なのかを考えて式を作りました。
1/n=1/2-a/(a+1) で、n=3 のとき、a=1/5 がでました。
これで、分子が2のときが可能になりました。
ksさんからのコメントです。(令和2年4月23日付け)
なるほど、分かりました。一般に、m/2n=1/2 -a/(a+1) と式をたて、a=(n-m)/(n+m) とすれ
ばよいのですね。
但し、これだと皆同じ細長い平行四辺形になります。更に条件をつけ、内部にあるように
としてもパンの耳を切るようにして、後は、同様にすればよい。思い描いたような解、図形に
したいですけど。
