�����w�̘b��@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@���E�Ŗ����w�ɖ�����ꂽ�l������B���̐l�Ƃ́A�A���v���q�g�E�f���[���[�i1471�`1528�j�B
�j���[�����x���O���܂�̔ނ́A�h�C�c�ɊG��Ȋw���������݁A�P�T�P�S�N����̓��ʼn�u��
�����R���A�v�̒��ɁA�E�}�̂悤�Ȗ����w��`���Ă���B�����w�̍ʼn��i�̒����̂Q�̐���
�Ȃ���A���傤�ǐ���N�ƂȂ�悤�Ȓ��ڂ��C�����c���Ă���B
�@���{�ł��A�����E������s���Z���^�[�̒��̊K�i�̕ǂɁA��
�Ƃ̈�����뎁����̖����w���`����Ă���B
�@�����w�ƈ���ɂ����Ă��A���푽�l�Ȗ����w�����݂���B���j
��A�����w�����߂ďo������̂́A�����̑O������i�a�D�b�D�P��
�I���j�ł���炵���B�E�}�̖����w�͊��ɂP�R���I�̒����̐��w
���ɏo�Ă���悤�Ȃ̂ŁA�ނ͉������ł����m�����炵���B
�����ł͊�{�I�Ȗ����w�̏Љ�Ƃ��̍������Љ�����Ǝv���B
|
�@ |
�R�~�R�����w
 |
�@�@�@�c�E���E�߂̂R�̐��̘a���A����
�@�@����P�T�ł���悤�ɁA�P�`�X�@�̐�����
�@�@�z�u������@�́A�{���I�ɂ́A�P���
�@�@�����Ȃ��B
�@�@�@���̍����́A�P�V���I�t�����X��
�@�@�o�`�G�[�ɂ��l�Ă��ꂽ�B
�@�@�E�}�̂悤�ɂS�̏��ڂ��͂ݏo��
�@�@���A�����������L�����A�͂ݏo����
�@�@��������ֈړ�������悢�B
�@�@�@���̍����́A��ʂ̐l�𖣗�����
�@�@�悤���B�i�Q�l�j |
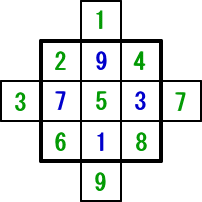 |
�@���̖����w�̊o���̂Ƃ��āA���̂悤�Ȃ��̂��m���Ă���B
�@�����Ǝv���ȁ@���O�@�Z��V��Ƀn�`���h��
�@294�@�@�@�@�@�@�@753 �@�@61�@�@�@�@�@�@8
�@��~��̃^�C�v�̖����w�́A���̕��@�ɂ��A�K�����߂���B
�@���̂��Ƃ��C�ɂȂ��Ă����̂ŏؖ����Ă݂��B�i�����R�P�N�P���S���t���j
�@�R�~�R�����w�́A��]�Ɨ��Ԃ��ꎋ����ƁA�P��ނ����Ȃ��B
�i�ؖ��j�@�R�~�R�����w��
�@�` �a �b
�@�c �d �e
�@�f �g �h
�Ƃ���ƁA�@�`�{�d�{�h���P�T�A�a�{�d�{�g���P�T�A�b�{�d�{�f���P�T
�@�R���𑫂��āA�@�i�`�{�a�{�b�j�{�R�d�{�i�f�{�g�{�h�j���S�T
�@�`�{�a�{�b���P�T�A�f�{�g�{�h���P�T�@�Ȃ̂ŁA�@�R�d���P�T�@���A�@�d���T
�@�`���P�@�Ɖ��肷��ƁA�h���X�@�ƂȂ�B
�@���̂Ƃ��A�@�P�{�a�{�b���P�T�@�ŁA�a���W�@�Ȃ̂ŁA�@�b���U
�@�܂��A�@�b�{�e�{�X���P�T�@�ŁA�e���Q�@�Ȃ̂ŁA�@�b���S�@�ƂȂ�A����͖����ł���B
�@����āA�a���P�@���m�肵�A�g���X�@�ƂȂ�B
�@���̂Ƃ��A�`�{�P�{�b���P�T�@���A�@�`�{�b���P�S�@�Ȃ̂ŁA�@�`���U�@�A�b���W�@���m�肷��B
�@����āA�@�f���Q�A�h���S�A�c���V�A�e���R�@�ƈ�ӂɊm�肷��B�@�@�i�؏I�j
�i�NjL�j�@���g�o�����������b�ɂȂ��Ă���g�m�u�����v����̃R�����g�ł��B
�@�@�@�i�����Q�W�N�P�P���Q�V���t���j
�@�R�~�R�����w�́A��]�A���]�ꎋ����ƁA��ʂ�ł��邱�Ƃ��킩���Ă��܂��B������
���߂āA�c���̘a���������������Ƃɂ���ƁA���̋^�������w�͉��ʂ肠��ł��傤�H
�@�炷���邳��̃R�����g�ł��B�i�����Q�W�N�P�P���Q�V���t���j
�@��]�A���]�A�s�̓���ւ��A��̓���ւ��ꎋ����ƁA��ʂ肵���Ȃ��B
(�ؖ�)�@�e�s�e��̍��v�͂P�T�B�R���̘a����ɂȂ邽�߂ɂ́A
�@��R�@�܂��́@�����Q�{��P��
�łȂ���Ȃ�Ȃ��B�����͂S�Ȃ̂ŁA�R�s�̂����A
�@�Q�s�������Q�{��P�A�P�s����R�B
�@������l�B�]���āA�s�E������ւ���A
�@����
�@����
�@����
�ƂȂ�̂ŁA���̔z��̂ݍl����Ηǂ��B
�@��R�ō��v���P�T�ɂȂ�̂́A�P�{�T�{�X�ƂR�{�T�{�V�����Ȃ�����
���S�͂T�ƂȂ�A��]�E���]����A
�@*1*
�@357
�@*9*
�ƂȂ�B����ƁA�W�͍���ɂ�������Ȃ��̂ŁA
�@816
�@357
�@492
�̂悤�Ɏc��͂��ׂĎ����I�Ɍ��܂�B
�@�]���āA��]�E���]�E�s�̓���ւ��E��̓���ւ��ꎋ����ƁA���̈�ʂ肵���Ȃ��B
# ��]�E���]�̂ݓ��ꎋ���A�s�E��̓���ւ��ꎋ���Ȃ��ꍇ�́A���S�ɂP�`�X�̂ǂ�
�@��u�����̈Ⴂ�����ł��̂ŁA�X�ʂ�ɂȂ�܂��B��]�E���]�����ꎋ���Ȃ��ꍇ�́A
�@�X�~�S�~�Q���V�Q�ʂ�B
�@��������̃R�����g�ł��B�i�����Q�W�N�P�P���Q�W���t���j
�@�炷���邳��A���肪�Ƃ��������܂����B�P����X�܂ł̐����g���č���������w�̊e�����`
�{���āA�a�������Ƃ�͂�A�قȂ鐔�X�̐��Ŗ����w������܂��B�Ƃ��낪�A����ɓ���
�͂܂�Ȃ������w������A��ʉ��ɒ��킵�Ă݂܂����B
�@�u�قȂ�X�̐����Ŗ����w������v
�@�ŏ��ɐ^�ɁA�K���Ȑ��l�Ă͂߂܂��Ba��b����a��2b�ƂȂ鐮��������ԁB
�@�l�|���@�@�C�l�{���{���C�l�|��
�@�l�|���{���C�l�@�@�@�@�C�l�{���|��
�@�l�{���@�@�C�l�|���|���C�l�{��
�@����ŁA���ׂĂ̂R�~�R�̖����w���J�o�[�ł���v���܂����A�ǂ��ł��傤�B
�@�炷���邳��̃R�����g�ł��B�i�����Q�W�N�P�P���Q�W���t���j
�@�ua��b����a��2b�ƂȂ鐮���v�ł͂�����Ƃ܂����ł��ˁB�Ⴆ�Aa=-b�Ƃ�2a=b�̂Ƃ�����
�w�ɂȂ�܂���B�u0��b��a����a��2b�ƂȂ鐮���v�Ƃł�����悢�Ǝv���܂��B
�@��������̃R�����g�ł��B�i�����Q�W�N�P�P���Q�W���t���j
�@���肪�Ƃ��������܂��B+a,-a,+b,-b���łĂ���̂ŁA��Βl���A�������Ȃ��ɂ���A�悩��
���ł��傤���H
�@�炷���邳��̃R�����g�ł��B�i�����Q�W�N�P�P���Q�W���t���j
�@a�Ab�ɕ��������Ă��܂��ƁA��]�E���]�ꎋ���������w��a�Ab����Έ�ɑΉ����܂���
�ˁB�u0��b��a����a��2b�ƂȂ鐮���v�Ƃ��Ă����A�����w���^����ꂽ���ɁAa�Ab���B���
���܂�܂��̂ŁA���̂悤�ɒ�`���Ă����������Y��ł悢�Ǝv���܂��B
�@�Ⴆ�A
�@816
�@357
�@492
�Ƃ��������w���������Ƃ��A�p�̒l���A(�E��)��(����)��(�E��)��(����)�@�ƂȂ�悤�ɉ�]�E
���]���āA
�@492
�@357
�@816
�Ƃ��邱�ƂŁAks����̏����ꂽ���Ԓʂ�ɂȂ�AM=5�Aa=3�Ab=1 �ƌ��܂�܂��B
�@��������̃R�����g�ł��B�i�����Q�W�N�P�P���Q�X���t���j
�@���������A���肪�Ƃ��������܂��B���߂āA��`�̊Ȗ����������܂����B�m�F�̂��߁A
(�P�C�R)�A(�|�P�C�R)�A(�P�A�|�R)�A(�|�P�A�|�R)�ׂ�ƁA�{���I�ɓ������̂��A�܂�Ԃ��̊W
�ɂȂ��Ă��邱�Ƃ�������A���\���܂����B
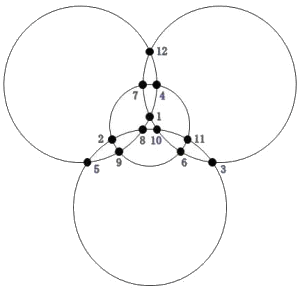
�@�R�~�R�����w�ɑ��āA�����~�����̃^�C�v�̖����w�̈�ʓI��@���L�q���邱�Ƃ́A��
���Ԃ����B
�S�~�S�����w
 |
�@�@�c�E���E�߂̂S�̐��̘a���A���ꂼ��R�S�ł���悤�ɁA
�@�P�`�P�U�@�̐�����z�u������@�́A�S���ŁA�W�W�O��ނ���B |
�@�����̈�̗�Ƃ��āA���̃}�j���G���E���X�R�u���X�̕��@���m���Ă���B�@�@
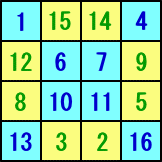 |
�@�@���}�̂悤�ɂP�U�̏��ڂ��Q�F�ɐF��������B����̏���
�@���珇�����ɐ������L������킯�ł��邪�A���F�̏��͏���
�@����ŁA���F�̏��͕ۗ�����B�E���܂ŏ����I�������A���x
�@�͋t�ɁA�E�����牡�ɏ����������L�����邪�A���̍ہA�F
�@�͕ۗ����āA���F�ŏ������ށB
�@�@���̂悤�ɂ��đS�Ă������������w�����}�ł���B
�@�S�~�S�����w�̓����Ƃ��āA�S�̐��̘a���R�S�ƂȂ�u���b�N
�@�́A�V�ӏ�����B����T���Ă݂ĉ������B |
�@�܂��A�S�i�@�𗘗p���ċ��߂���@���m���Ă���B4�i�@�ŁA�O�`�P�T�@�͎��̂悤�ɕ\��
���B
| �\�i�@ |
�O |
�P |
�Q |
�R |
�S |
�T |
�U |
�V |
�W |
�X |
�P�O |
�P�P |
�P�Q |
�P�R |
�P�S |
�P�T |
| �S�i�@ |
�O�O |
�O�P |
�O�Q |
�O�R |
�P�O |
�P�P |
�P�Q |
�P�R |
�Q�O |
�Q�P |
�Q�Q |
�Q�R |
�R�O |
�R�P |
�R�Q |
�R�R |
�@�S�i�@�ł͊e�ʂ̐����́A�O�`�R�@�Ȃ̂ŁA�c�܂��͉��ɗB�����悤�Ɂ@�O�`�R�@��z�u
���������w���Q���B��������̂����āA�S�i�@�̖����w�����B
������\�i���ɒ����A
 |
�@�@���̊e���ɂP�������āA
�@���߂閂���w��B�i�E�}�j |
�@�@ |
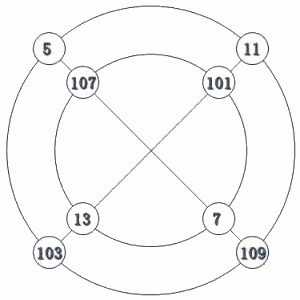
�܂��A�����w�Ɋւ��āA���̂悤�Ȗʔ�����肪�m���Ă���B
 |
�@�@���}�̖����w�ɂ����āA�` �� �a �̒l��
�@���߂�B
�@�i���j�E�}�ɂ����āA�`�ɁA����݂Ԃ���
�@�Q�A�R�A�S�A�U�A�V�A�W�A�P�P�A�P�Q�A�P�R�A�P�S�A
�@�P�U�@�������āA���A���A���@�ɖ�������
�@�����̂�T���ƁA
�@�@�@�`���S�A�����P�S�A�����P�U�A�����V
�@�̏ꍇ�̂ݓK����B���l�ɂ��āA�a�ɁA
�@����݂Ԃ��ɁA
�@�@�@�@�Q�A�R�A�U�A�W�A�P�P�A�P�Q�A�P�R
�@�������āA�K����ꍇ�����߂�ƁA
�@�@�@�a���P�P�A�����Q�A�����W�@�̂݁B
�@���������āA�`���S�A�a���P�P�@�ł���B |
 |
| ���l�ɁA���̖��͔@�����낤���B |
 |
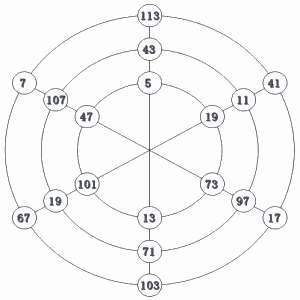
�@�i���j�@�E�}�����āA�����w�̐�������
�@�@���{�`���P�S�@�ł���B����āA�����P�U
�@�@�܂��A�`�{�����P�Q�@�ł���B
�@�@�����w�̐�������A
�@�@�`�{���{���{B���R�S�@�����藧�̂�
�@�@�a���U�@�ł��邱�Ƃ�������B
�@�@���ɁA�`�����肵�����̂����A������
�@�@�����B�S�i�@�W�J�𗘗p���ċ��߂Ă�
�@�@�悤�B |
�@ |
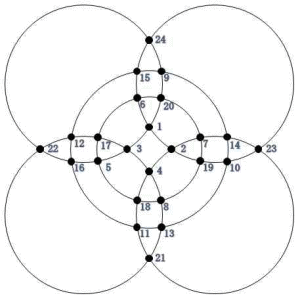
�@�^����ꂽ�����w�ŁA�e���ڂ̐�����P�����������S�i�@�ɒ����ď����Ă݂�ƁA
�@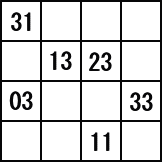
�@���̖����w�́A���̓�������A���̂Q�̖����w�̍����ō��ꂽ���̂ł���B
�@ �@�@
�@�@
�����A
�@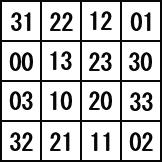 �@
�@
�@���̂��Ƃ���A���߂�`�̒l�́A�Q�O�i�S�i�@�j���\�i���ɒ����āA�P��������A�`���X�@��
����B
�@�����ɍ�������ƁA���߂�`�̒l���B��ł���Ǝ��M�������Č����Ȃ��B������������A
�����Ƃ��邩������Ȃ��B�i�`�̉\���Ƃ��ẮA�P�A�R�A�T�A�X�A�P�P�̏ꍇ�����Ȃ����D�D�D�B�j
�@���̓_���܂߂āA�S�i���W�J�ɂ����@�łȂ���@�������m�̕�����������Ⴂ�܂�����A
�m�������[�������肢���܂��B
�i�lj��j�@��L�̉��̕s�m���������邽�߂ɍčl������A��͂�A���͂P�ʂ�ł͂Ȃ���
�@�@�@�@���B�`�̒l�Ƃ��āA�P�A�R�A�T�A�P�P�@�̊e�ꍇ�ɂ��Č��������ʁA�`���R�A�T�A�P�P�@��
�@�@�@�@�ꍇ�́A�����w���̂��̂����݂��Ȃ��B����ɁA�`���P�@�̂Ƃ��A���̂悤�Ȗ����w��
�@�@�@�@���݂���B
�@
�@���������āA���̓��́A�`���P�@�܂��́@�X�@�A�a���U�@�ƂȂ�B
�i�Q�l�����F�z�[���y�[�W�u��s�D���������v
�@�@�@�@�@�@�@ �D�R�ǎO�@���@�g�߂Ȑ��w�̗��j�i���m�}���j�j
�i�NjL�j�@��~��̃^�C�v�̖����w�ɂ��āA��L�̕��@�ŕ��ʋ��߂��邪�A���̋�
�@�@�@�@�ߕ��̕ό`�o�[�W����������������悤���B
�@�i��j�@���ڂ݂̂͂����̂����ɁA���郋�[���ɏ]���āA�����߂Ă������@
�@�@���̕��@�́A�݂͂������g��Ȃ����A���[����m��Ȃ����̂ɂƂ��ẮA�u�}�W�b�N�I�v��
�@���Ԃ��炢�����������������m��Ȃ��B
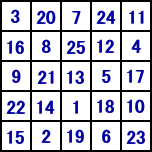 |
�@�@�����L���̃��[��
�@�@�P�D�@�ߍ�������ɁA�P���珇�Ԃɐ������L��
�@�@ �Q�D�@�g�O�ɂ͂ݏo�����ꍇ�̑Ώ�
�@�@�@�@�@�E�@�����̏ꍇ�́A���̗�̑�P�s�i�ŏ�i�j�ɋL��
�@�@�@�@�@�E�@�����̏ꍇ�́A���̍s�̑�T��i�E�[�j�ɋL��
�@�@�@�@�@�E�@�Ίp���̏ꍇ�́A��P��i���[�j�̑�Q�s�ɋL��
�@�@ �R�D�@�������d�Ȃ����ꍇ�̑Ώ�
�@�@�@�@�@�u���v�̎��ɋȂ����āA�E���ׂɋL�����A���̌��ʂ͂ݏo��
�@�@�@�@�ꍇ�́A��́@�Q�D�@�̃��[���ɏ]���B |
�@���̃��[�����}�X�^�[���邽�߂ɁA�����̖����w��ڂŒǂ��Ă݂Ă��������B
�@�p��̐搶�ɖ����w�̍������f������A���̂悤�ɂ��̂���ԕ�����₷���Ƌ���
�����B
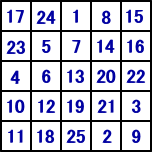 |
�@�@�����̋L���������߉E�オ��Ƃ������Ƃ������A��{�I�ȃ�
�@�[���͏�̏ꍇ�Ƒ�̓����ł���B�i�E���A�㉺�@�̓Ǒւ��͕K�v�j
�@��������I�ɈႤ�̂́A�u�������d�Ȃ����ꍇ�̑Ώ��v�̕��@�ł�
�@��B���}���݂�ƁA�������d�Ȃ�����A�d�Ȃ�O�̐����̉��ɋL��
�@���Ă���B����ɁA�Ίp����ɂ͂ݏo�����ꍇ�����l�ɏ������Ă���B
�@�@�R�~�R�̖����w�߂Ă݂�ƁA���͂��̕��@�ō���Ă��邱��
�@�����������B |
�@�ȏア����ɂ��Ă��A�d�v�Ȃ��Ƃ́A�����́u�P�v�̈ʒu�ł���B�Q�T�ʂ�S�Ăɂ��Č���
�������ʁA�����w���o����̂́A�P�̃��[���ɂ��A�P�̏ꍇ�����Ȃ����Ƃ��m�F����
���B
�@�R�~�R �̖����w�́A��{�I�ɂP��ނ����Ȃ����A�T�~�T �̖����w�́A��̗Ⴉ���������
�悤�ɍŒ�Q��ނ͂���悤�ł���B���������{���ɈႤ���͉̂��ʂ肠��̂��A����̌�
�����҂����B���������������̕��A�m�������[���ł��m�点���������B
�i�Q�l�����F�������Y�@���@�}�`�p�Y���@�B�A���J���g�i�����o�Łj�j
�i�ĒNjL�j�@�����_�ƃf���[���[�̍�i�o���ɋ����������A�`���Ɍf�����f���[���[�̖���
�@�@�@�@�@�w�����������������邱�Ƃ��ŋߒm�����B�A�����J�̓E�B�X�R���V���B�}�f�B�\���o�g
�@�@�@�@�@�̃}�[�N�E�R�����Y�Ƃ������ł���B
�@�ނ́A�e���ڂ̐�������P�������������Q�i���ɒu�������āA�ʔ������������Ă���B
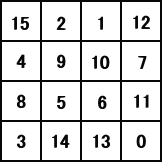 |
�@�@���̖����w�̊e�������Q�i���ɒu��������ƁA���}��B
�@�@
�@�@�@�@�@�@�@�@�@�@ |
�@���̂Q�i���\�����ꂽ���̂��A�����ƒ��߂Ă���ƁA���낢��ȓ����ɋC�Â���邱�ƂƂ�
�v���B���ӎ������₷���悤�ɁA�F�����Ē��߂Ă݂悤�B
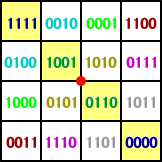 |
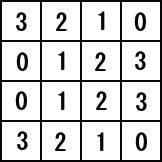
�@�@�܂��A���F�̑Ίp����̐��́A�����F���m�݂��ɂO�ƂP�̓�
�@��ւ��ɂȂ��Ă���B����ɁA���̑Ίp���Ɋւ��đΏ̂Ȉʒu
�@�ɂ��鐔�͓����F���m�݂��ɐ����̏��Ԃ��t�ɂȂ��Ă���B
�@���F�łȂ��Ίp���Ɋւ��Ă��A���l�Ȍ��ۂ������o����B�����A
�@���F�łȂ��Ίp����̐��́A�����F���m�݂��ɐ����̏��Ԃ�
�@�t�ɂȂ��Ă���B���̑Ίp���Ɋւ��đΏ̂Ȉʒu�ɂ��鐔�́A
�@�݂��ɂO�ƂP�����ւ��������̏��Ԃ��t�ɂ��Ă���B
�@���̖����w�ɂ͂����Ƃ��낢��Ȑ���������ł���̂��낤�B |
�@�}�[�N�E�R�����Y�͂���ɁA���̂悤�Ȃ��Ƃɂ��C�Â��Ă���B
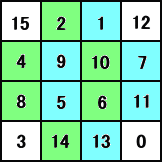 |
�@�@�@���}�̂悤�ɁA�����͋������m�A��͊���m�ŐF����
�@�@����ƁA�ւ����܂��Ă���}��z�����邱�Ƃ��ł���B
�@�@�@���̂悤�ɁA�P�Ȃ��̖����w�Ƃ͂����A���낢��_��I��
�@�@�������������邱�Ƃɋ��������B |
�i�Q�l�����F�N���t�H�[�h�E�`�E�s�b�N�I�[�o�[�@���@��쌳���@��
�@�@�@�@�@�@�@�@�����_�[�Y�@�I�u�@�i���o�[�Y�i���̕s�v�c�j�@�i��w�̗F�Ёj�j
�i�NjL�j�@�ŋ߁A�ߏ��̐}���قŁA�����낵�����͂���{�ɏo������B
�@�@�@�@�@��X�����@���@�V�ҁ@���@���@�w�@�i�y�R�[�j
�@���̖{�ł́A���̒��ɑ��݂���A����Ƃ����閂���w�̘b�肪�A�M���E�M���E�ɋl�ߍ���
��Ă��銴���ŁA�ǂގ҂��A�u����ł����A����ł����v�ƈ��|����B���ɁA�����Ȃ̂́A
�@�S�~�S�����w�@�S�W�W�O��̏Љ� �F ���D�T�U �` ���D�X�U
�@�S�~�S�����w����V�����S�~�S�����w�������@ �F ���D�X�U �` ���D�P�O�X
�@�����w�쐬�̃v���O�����W�i�a�`�r�h�b�A�b �Ȃǁj �F ���D�Q�O�X �` ���D�Q�V�P
�ł���B�܂��A�T�~�T�����w�́A�Q���V�T�R�O���T�Q�Q�S��ނ��邱�Ƃ�������Ă���B
���҂́A�Ȗ،��̌������Z�̐搶�ŁA���̔��w�Ԃ�ɂ́A����������v���ł���B
�i�NjL�j�@�z�[���y�[�W�ɂāA����́u�����w�̌����v�ɂ��Ă̐��ʂ����J���Ă������
�@�@�@�@�@���������邱�Ƃ��A�ŋߒm�����B
�@�@�w�����w�̊�b�I�����x�@�ۓc�@���� ��
�@ �@�@�@ �@���_�@�@��P�́@�����w�Ƃ͉���
�@�@������́A�u�����p�Y������v�̖��؎�����ɋ����܂����I�i���Ӂj
�i�NjL�j�@�u�����p�Y������v�̖��؎�����A�܂��܂��������������܂����B�i���ӁI�j
�����w�ɂ��Ă̏���������lj����Ă����܂��B�ȑO�A���k���ؖr�������̖����w
�̃z�[���y�[�W���������̂ł����A�ފ��ƂƂ��ɕ�����Ă��܂��܂����B
�@�p��ł̃y�[�W���c���Ă��܂��B
�@���@http://mathforum.com/te/exchange/hosted/suzuki/MagicSquare.html�i�����N��j
�@���ۂɖK�₵�Ă݂��Ƃ���A���낢��ȃ^�C�v�̖����w���Љ��Ă��āA��C�ɂ͓ǂ݂�
��܂���ł����B�������Ԃ��o�����Ƃ���ŁA�������荘�𗎂������ēǂ�ł݂����Ǝv���܂��B
�ł��A�p��ł̃y�[�W�����Ƃ������Ƃɂ͂Ȃ�Ȃ��ł���ˁH�I�i�Q�O�O�R�D�W�D�Q�O�L�j
�i�NjL�j�@�����P�W�N�W���P�S���t��
�@���A�ċx�݂𗘗p���āA�u�e���������v������Ă���B�u�m�����L�v�ł́A�C���X�g�[���̃g���u��
�������āA�C���X�g�[���Ɏ��s�����Ƃ����b���������A�}�V���i�����g�o�̍X�V�Ɏg���Ă���j
��ς��čēx�C���X�g�[���ɒ��킵����A���Ƃ������ɂł����݂����B�i����͉��́H�j
�@�܂������n�߂ĊԂ��Ȃ��̂ŋZ�p�I�ɖ��n���Ǝv���邪�A��i�������Ă݂��B
�i���̍�i������������̂ɁA��������������v�����I������Ɖɂ��ȁH�j
�@�����w��������������̂ŁA�����𐳂����ꏊ�ɓ\��t����悢�̂����A�ʒu������
���Ȃ��Ƃ͂�����Ă��܂��B�ʒu���������ƁA���̏ꏊ�ɐ������z�������B
�@���̍�i�ŁA���ЗV��ł���Ă��������B���z�́A�������ցB���ǂ̎Q�l�ɂ������Ǝv����
���B
�@�Z�L�����e�B�ی�̂��߁A�R���s���[�^�ɃA�N�Z�X�ł���A�N�e�B�u�@�R���e���c���\������Ȃ��悤�ɁA
�h���������������@�d���������������@�Ő������Ă���ƁA�g�s�l�k�ŁA�e���������łƂ��Ɍ����܂���B�u���b�N����Ă���
�R���e���c�������Ă��������B�i���݂܂���A���Ȃ̐ӔC�ł��肢���܂��B�j
�e���������Ł@���@�@�����w �e�������� �ŗV�ڂ��I
�g�s�l�k�Ł@���@�@�����w �e�������� �ŗV�ڂ��I
�i�R�����g�j�@�������ꏊ�ɓ��邱�Ƃ͓���̂����A���������������Ă��Ȃ��ł��ˁI�Q�̃C
�@�@�@�@���X�^���X�̍��W�̍��킹����������ł��B�ł��A���������e���������̊�b�̊�b���A
�@�@�@�@��i������Ă݂āA���ƂȂ����������悤�ȋC�����܂��B
�@�R�P���Ԃ݂̖̂����̌��łȂ̂ŁA�撣���đ��̍�i�ɂ����킵�����Ǝv���܂��B�ڕW�́A
���̂g�o�̃R���e���c�̃C���^���N�e�B�u���ł��I�ł��邩�ȁH
�@�Ƃ���ŁA�R�P���Ԃ̖����̌����Ԃ��߂�����A��i�������Ȃ��Ȃ�Ȃ�Ă��Ƃ͂Ȃ��ł�
��ˁH
�i�NjL�j�@���g�o�����������b�ɂȂ��Ă���g�m�u�f�`�h�v����̂����e�ł��B
�@�@�@�i�ߘa���N�T���Q�O���t���j
�@�u�Q�O�P�X�v�����Ƃɑf�������w������Ă݂܂����B�T����ꂽ�̂ŁA2019�N�͑f���Ƃ̑�
���͐[���ƍl���Ă����̂ł��傤���H
+----+----+----+
| 229| 907| 883|
+----+----+----+
|1327| 673| 19|
+----+----+----+
| 463| 439|1117|
+----+----+----+ |
�@ |
+----+----+----+
| 277| 859| 883|
+----+----+----+
|1279| 673| 67|
+----+----+----+
| 463| 487|1069|
+----+----+----+ |
�@ |
+----+----+----+
| 283|1009| 727|
+----+----+----+
|1117| 673| 229|
+----+----+----+
| 619| 337|1063|
+----+----+----+ |
| �@ |
|
|
|
|
+----+----+----+
| 313| 739| 967|
+----+----+----+
|1327| 673| 19|
+----+----+----+
| 379| 607|1033|
+----+----+----+ |
|
+----+----+----+
| 463| 733| 823|
+----+----+----+
|1033| 673| 313|
+----+----+----+
| 523| 613| 883|
+----+----+----+ |
|
|
�@�ߑΊp�����n�j�ł��B
�@�炷���邳��̃R�����g�ł��B�i�ߘa���N�T���Q�O���t���j
�@�{���Ɂu2019�N�͑f���Ƃ̑����͐[���v���ǂ������ׂĂ݂܂����B�f�����@�w�����邽
�߂ɂ͏��Ȃ��Ƃ�(�f��)�~3�łȂ���Ȃ炸�A2019�͊m���ɂ�������Ă��܂��B
�@�������A(�f��)�~3�Ƃ������͖����ɂ���܂��B�������f�����傫���Ȃ�Ȃ�قǍ���
�f�������w�̌��͑�����X���ɂ���܂��̂ŁA�傫���f���Ɣ�r���Ă������͂킩���
����B
�@�����ŁA2019�ߕӂ�(�f��)�~3�ō���f�����@�w�̌��ׂĂ݂�ƁA
1923: 6�@�@1929: 6�@�@1941: 4�@�@1959: 2�@�@1977: 3�@�@1983: 1�@�@2019: 5�@�@2031: 4
2049: 12�@�@2073: 1�@�@2103: 12�@�@2127: 2�@�@2157: 7�@�@2181: 10�@�@2199: 7�@�@2217:
4
2229: 2�@�@2253: 5�@�@2271: 3�@�@2283: 1
�ƂȂ�܂��B2031�ȉ��ł�10�ʂ�ȏ������̂͂���܂���̂ŁA2049��10�ʂ�ȏ�Ƃ�
��ŏ��̐��ł��B
�@���ꂾ�����Ă��悭�킩��Ȃ��Ǝv���܂����A���̌�́A2319�A2427��10�ʂ肸�ł����
�̂́A2433�`3063��32�͂��ׂ�10�ʂ薢���ŁA2000�ȍ~�ŋ}�ɑ����Ă���킯�ł͂���
�܂���B�����Ƃ��A6000�ȏ�ɂȂ�ƂقƂ��2���ɂȂ�܂����B
�@���20�̃f�[�^�̍��v��97�A���ς�4.85�ł�����A2019�N�́u5�v�͂قڕ��ςɋ߂��l
�ł��B
�@����āA2019�N�́A(�f��)�~3�̒��ł͑f���Ƃ̑����́u���ʁv�ł���A���Ɂu�������[���v
�Ƃ����قǂ̂��̂ł͂Ȃ��Ǝv���܂��B
�@2049�N�Ȃ�u�������[���v�ƌ�����Ǝv���܂��̂ŁA30�N��ɂ܂����e���ĉ�����(��)
�@�f�`�h ����̃R�����g�ł��B�i�ߘa���N�T���Q�P���t���j�@
�@�u�Q�O�S�X�v�̑f�������w�A���ʑO�ɁA���ꂾ���͍�肽�������B
+----+----+----+
| 173|1103| 773|
+----+----+----+
|1283| 683| 83|
+----+----+----+
| 593| 263|1193|
+----+----+----+ |
�@ |
+----+----+----+
| 179|1013| 857|
+----+----+----+
|1361| 683| 5|
+----+----+----+
| 509| 353|1187|
+----+----+----+ |
�@ |
+----+----+----+
| 179|1097| 773|
+----+----+----+
|1277| 683| 89|
+----+----+----+
| 593| 269|1187|
+----+----+----+ |
�@ |
+----+----+----+
| 263| 977| 809|
+----+----+----+
|1229| 683| 137|
+----+----+----+
| 557| 389|1103|
+----+----+----+ |
| �@ |
|
|
|
|
|
|
+----+----+----+
| 263|1013| 773|
+----+----+----+
|1193| 683| 173|
+----+----+----+
| 593| 353|1103|
+----+----+----+ |
|
+----+----+----+
| 347| 719| 983|
+----+----+----+
|1319| 683| 47|
+----+----+----+
| 383| 647|1019|
+----+----+----+ |
|
+----+----+----+
| 353| 719| 977|
+----+----+----+
|1307| 683| 59|
+----+----+----+
| 389| 647|1013|
+----+----+----+ |
|
+----+----+----+
| 353| 809| 887|
+----+----+----+
|1217| 683| 149|
+----+----+----+
| 479| 557|1013|
+----+----+----+ |
| �@ |
|
|
|
|
|
|
+----+----+----+
| 353| 977| 719|
+----+----+----+
|1049| 683| 317|
+----+----+----+
| 647| 389|1013|
+----+----+----+ |
|
+----+----+----+
| 383| 857| 809|
+----+----+----+
|1109| 683| 257|
+----+----+----+
| 557| 509| 983|
+----+----+----+ |
|
+----+----+----+
| 383| 947| 719|
+----+----+----+
|1019| 683| 347|
+----+----+----+
| 647| 419| 983|
+----+----+----+ |
|
+----+----+----+
| 479| 797| 773|
+----+----+----+
| 977| 683| 389|
+----+----+----+
| 593| 569| 887|
+----+----+----+ |
�i�NjL�j�@���g�o�����������b�ɂȂ��Ă���g�m�u�f�`�h�v����̂����e�ł��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�ߘa���N�X���U���t���j
�@�S�~4�s��ŁA
�@1, 8, 13, 12
�@ 14, 11, 2, 7
�@4, 5, 16, 9
�@ 15, 10, 3, 6
�Ɣz��A�e�s�A�e��A�e�Ίp���i�Q�̎�Ίp���ȊO��14+5+3+12�Ȃǁ��̑Ίp����
�܂ޑS���łP�U�����j�����ׂĘa34���������w���ł���B
�@�����ŁA1�`25�̐�������g�p���āA5�~5�ł̖����w�ɒ��킵�Ă݂ĉ������B
�i�R�����g�j�@���킵�Ă݂܂����I���̗Ⴊ������܂����B����́A�f�`�h����̏�������
�@�@�@�@�@�@�܂��B�T�~�T�̖����w�œ���
�@
����ɁA�s�̒u�������{���ē��邱�Ƃ��ł��܂����B
| 16 |
8 |
25 |
12 |
4 |
| 15 |
2 |
19 |
6 |
23 |
| 9 |
21 |
13 |
5 |
17 |
| 3 |
20 |
7 |
24 |
11 |
| 22 |
14 |
1 |
18 |
10 |
�@�u�����w�̎����v�ɂ��āA��������̃R�����g�ł��B�i�ߘa�R�N�P���Q�T���t���j
�@3�~3�̖����w�̋K���ɂ����������W�܂���l���܂��B��s���A���ׂē������L���Ӗ���
�l����Ɛ��^��ԂɂȂ�Ǝv���܂��B�����́A8�ł�낵���ł��傤���H
�@�u�����w�̐����v�ɂ��āA��������̃R�����g�ł��B�i�ߘa�R�N�P���Q�X���t���j
�@�P�`�X�ō�閂���w�B�c���ɎO�����Ęa���������̂͂������ł����A���[�c�O���
�悵�āA�E�[�c�O���悵���a���������B��[���O���悵�āA���[���O���悵��
�a���������B����ɁA�c���A�O�O���Ƃ݂Ȃ��āA���a�����ƁA����܂��������B
�@���`��ԂƂ��ẮA�����́A�R���S�ł����H
�@��������̃R�����g�ł��B�i�ߘa�R�N�P���R�O���t���j
�@�T�~�T�̖����w�ɂ��Ă��A�Q�A�Q��a�����藧���܂��B���w�́A�߂ɕ��ׂāA��
�̈ʒu�ɔz�u������@�ł��B�ݏ�a�����߂āA���C�ɓ���A�����w�̒��ɃI�A�V�X����
�܂����B
�@��������̃R�����g�ł��B�i�ߘa�R�N�S���R�O���t���j
�@�{���̖��@�w�́A�قȂ�P���炎�܂ł̂��̂ł����A���������������A�a�ƍ��A�X�J���[�{��
������Ԃ��l����ƃx�N�g����ԂɂȂ�悤�ł��B�R�~�R�̕��w�ł́A�������R�ɂȂ�悤��
���B�X�ɁA�s��̐ςɂ��Ă��A���Ă���悤�ł��B
�@���ׂĂׂĂ͂��܂��A���̂��~���ł�������ł��傤���H
�i�R�����g�j�@�R�~�R�̖����w�ɂ����āA
| �� |
�� |
�� |
| �� |
�� |
�� |
| �� |
�� |
�� |
|
�Ƃ���ƁA�������i���C���j�@�i���@���́A���A���ł����܂�Ƃ����Ӗ��j�@�ŁA����
�@�������i���C���j�@����A�������i���C���C���j�@�A�������i���C���C���j�@�A�������i���C���C���j�@�A�������i���C���C���j
�@���R�x���@���A���A���@�̂R�Ȃ̂ŁA�R�~�R�̖����w�́A�x�N�g����ԂƂ��ĂR�������Ƃ���
���Ƃł����ˁH
�i�NjL�j�@�u���~���w�v�Ƒ肵�āA���g�o�����������b�ɂȂ��Ă���g�m�u�f�`�h�v���炲���e
�@�@�@�@���������܂����B�i�ߘa�R�N�T���Q�P���t���j
(1)�@�_P�𒆐S�Ƃ������a5�̉~C��`���B
(2)�@C�̉~�����5��������_���Ƃ�B(P1�AP2�AP3�AP4�AP5�j
(3)�@���ꂼ�� Pi �𒆐S�Ƃ��锼�a4�̉~��`���B�iC1�AC2�AC3�AC4�AC5)
(4)�@�_P�𒆐S�Ƃ��锼�a4�A3�̉~��`���B(C6�AC7)
�@����ŁA8�̉~���`���A�~�Ɖ~�ŏo����v40�̌�_�����܂��B
�i8�̌�_���Ԃт�݂����܂J�����l�Ȗ͗l�ƂȂ�B�j
�@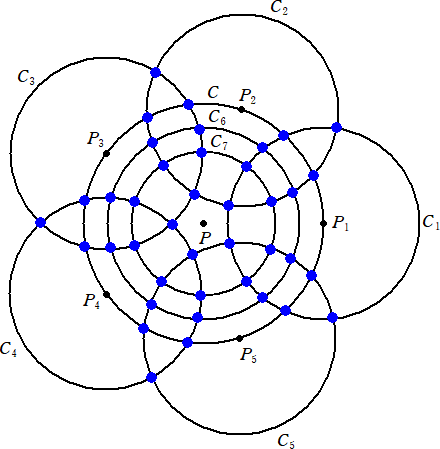
�@���āA����40�̌�_��1����40�܂ł̐�������K���ɔz�u����ƁA8�̉~�����
��10���̌�_�����݂��邱�ƂɂȂ邪�A�e�~����̌�_�ɔz�u���ꂽ���ł̘a���Ƃ�
�A�ǂ�� 205 �ƂȂ�l�ɔz�u���Ăق����B
�@�������A{1,2,3,���,40}����10�I�сA���̘a��205�ƂȂ�g��������10,388,788�i�ʂ�j����
�݂ł��邱�Ƃ����m�肨���������B
�@���āA���̖����ɑ��݂���g��������8�̑g�������i��o���邩�H
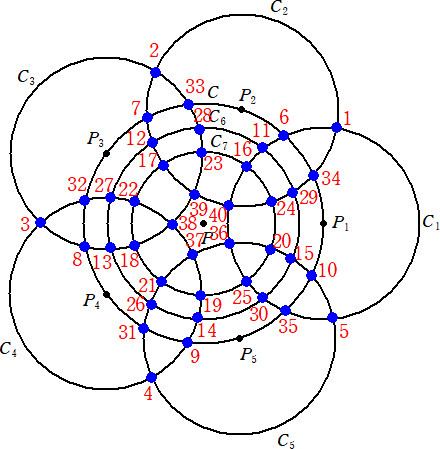
�@DD++����̃R�����g�ł��B�i�ߘa�R�N�T���Q�P���t���j
�@�ǂ� 2 �̉~���ڂ��邱�Ƃ��Ȃ��A�ǂ� 3 �̉~�� 1 �_�Ō���邱�Ƃ��Ȃ��킯�ł�����A
�݂��Ɍ����C�ӂ� 2 �~�̑g�ɂ��Č�_ 2 �̘a�� 41 �ɂȂ�悤�ɓK���ɖ��߂Ă���
�����ŏ���������̂ł́B
�i�R�����g�j�@DD++����̍l�����Ő����߂Ă݂܂����B
�@
�i�NjL�j�@�ߘa�R�N�U���S���t��
�@�����w�Ƃ����ƁA�ʏ�́A�u�c�E���E�߂̐��̘a�����v�ł��邪�A�u�c�E���E�߂̐��̐�
�����v�ł���|���Z�����w���l������B
�@�����A�����ɍ���Ǝv�����A�����̈�̕��@���Љ�����B
�@�����̃R�c�͊ȒP�ŁA�ݏ�̎w�������ɂ��āA�ʏ�̖����w���\���������̂����p
����悢�B�Ⴆ�A
| �P |
�O |
�Q |
| �Q |
�P |
�O |
| �O |
�Q |
�P |
|
���w���ɂ��ꂪ�Q�̐������A
| �Q�O�P |
�Q�O�O |
�Q�O�Q |
| �Q�O�Q |
�Q�O�P |
�Q�O�O |
| �Q�O�O |
�Q�O�Q |
�Q�O�P |
|
�� |
| �Q |
�P |
�S |
| �S |
�Q |
�P |
| �P |
�S |
�Q |
|
�@���l�ɂ��āA
| �P |
�O |
�Q |
| �Q |
�P |
�O |
| �O |
�Q |
�P |
|
���X�O����]�����āA
| �O |
�Q |
�P |
| �Q |
�P |
�O |
| �P |
�O |
�Q |
|
���w���ɂ��ꂪ�R�̐������A
| �R�O�O |
�R�O�Q |
�R�O�P |
| �R�O�Q |
�R�O�P |
�R�O�O |
| �R�O�P |
�R�O�O |
�R�O�Q |
|
�� |
| �P |
�X |
�R |
| �X |
�R |
�P |
| �R |
�P |
�X |
|
�@�ꂪ�Q�̂��̂ƒꂪ�R�̂��̂𐬕����Ɋ|�����킹��A�|���Z�����w�̊����ł���B
���Ȃ킿�A
| �Q |
�P |
�S |
| �S |
�Q |
�P |
| �P |
�S |
�Q |
|
�~ |
| �P |
�X |
�R |
| �X |
�R |
�P |
| �R |
�P |
�X |
|
�� |
| �Q |
�X |
�P�Q |
| �R�U |
�U |
�P |
| �R |
�S |
�P�W |
|
�@�c�E���E�߂̐��̐ς��A���ׂāA�Q�P�U�@�ƂȂ��Ă���B
�i�NjL�j�@�f�`�h ����������������܂����B�i�ߘa�S�N�S���V���t���j
�@�R���܂ł̑f�����g���A�R�~�R�̐����s��ɂX�̈قȂ�f���߂āA�c�A���A�߂�
���v���S�ē������v�ƂȂ���́i���v�l���ł��������������́j���\�����Ă��������B
�i�R�����g�j�@�u�Q�O�S�X�v�̑f�������w�A���ʑO�ɁA���ꂾ���͍�肽�������Ƃ����f�`�h ����̃R
�@�@�@�@�����g�i�ߘa���N�T���Q�P���t���j��q�����āA�����������̂Ƃ��āA���̏ꍇ����
�@�@�@�@��܂��ˁB
+----+----+----+
| 479| 797| 773|
+----+----+----+
| 977| 683| 389|
+----+----+----+
| 593| 569| 887|
+----+----+----+ |
�@�f�`�h ����̃R�����g�ł��B�i�ߘa�S�N�S���V���t���j
�@�u�R���܂Łv�ł��̂ŁA�P����Q���̑f�����g�p�\�Ɨ����肢�܂��B
�i�NjL�j�@�ߘa�U�N�P�P���Q�Q���t��
�@�{���t�̒����V�������ɁA�����w�̘b�肪���グ���Ă����B
�@�R�~�R�̖����w�́A�P�ʂ�
�@�S�~�S�̖����w�́A�W�W�O�ʂ�
�@�T�~�T�̖����w�́A�Q���V�T�R�O���T�Q�Q�S�ʂ�i�P�X�V�R�N�j
���邱�Ƃ��m���Ă��邪�A�U�~�U�̖����w�̌��ɂ��āA�R����w�̋����ł���ꂽ
���Z�p�r���A�R�O�N�����čU�����A
�@�P�V�V�T���R�W�W�X���P�X�V�U���U�O�U�R���T�U�R�Q�i�j
�ł��邱�Ƃ��A���E���̃p�\�R�����Q�N�ԓ����������ē���ꂽ�Ƃ����B���I�Ԃ�̉���
�ł���B�i���@�Q�l�j
�@kuiperbelt ����̃R�����g�ł��B�i�ߘa�U�N�P�P���Q�R���t���j
�@���~���w�ɂ��āA���k��w�@��ؖr�������̖����w�̉p��ł̃y�[�W
�@http://mathforum.com/te/exchange/hosted/suzuki/MagicSquare.html
�������N��ɂȂ��Ă��܂������A�S���͊m�F���Ă��܂��Awebarchive�ł܂��{�����邱
�Ƃ͂ł���悤�ł��B
�@�f�`�h����̗ߘa�R�N�T���Q�P���t���́u���~���w�v�ŁA
�@�u�V�Ł@�����w�̐��E�v�i��X�����A���{�]�_�Ёj�̑�8�́u���낢��Ȗ����w�v��p.276
�ɕʂ̉����ڂ��Ă��܂����B
�@�@
�i�R�����g�j�@DD++ ����̍l�����Ƃ͈Ⴄ��ł��ˁD�D�D�I��}�͌��ŁA�����́A���i�ɂ���
�@�@�@�@�@�܂��B�Q�S���t���ŁAkuiperbelt ����������܂����B
�@�u�����w�v�ɂ���
�@���~�w�Ƃ����āA���S�~�ƒ��a�������������āA���̌�_2n^2+1�ɐ�����u�����̂�
����܂����A���a���2n+1�̐����̘a�i�a�a�j�ƁA�~�����2n�̐��ƒ��S����2n+1��
���̘a(���a)��S�ē������������̂ŁA�u�k�P�Z�@�v�ɂ́A���S�̐���9�Ƃ��āA4�̓��S�~��
��
�@{7,22,10,24,25,18,2,30},{19,13,23,3,11,26,29,14},{31,1,16,15,5,17,32,21},{12,33,20,27,28,8,6,4}
��z���A4�{�̒��a���
{12,31,19,7,9,25,11,5,28},{33,1,13,22,9,18,26,17,8},{20,16,23,10,9,2,29,32,6},{27,15,3,24,9,30,14,21,4}
�Ƃ����u����}�v�Ƃ����}���ڂ��Ă��܂�(�u����v��9�ɏW�܂�Ƃ����Ӗ��B)�B
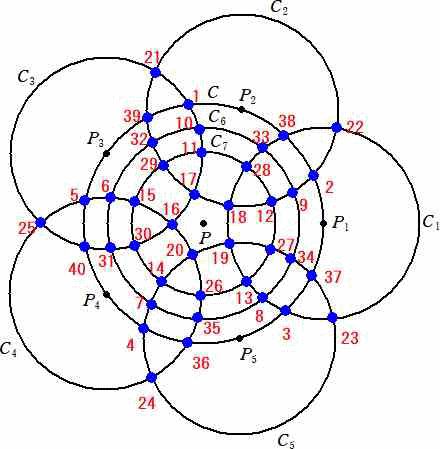
�@��������p���āA���}�̂悤�ɖk�ɂƓ�ɂŌ�������3�̑�~�ƁA�ԓ��A�k��45�x�A���
45�x��3�̈ܐ��̉~�̌�_�ƂȂ�20�̓_�ɁA1�`20�̐����������A3�̑�~��̐���
�a�ƁA3�̈ܐ��̉~��̐��Ɨ��ɂ̐��̘a��}�̂悤�ɓ����������u�����w�v���l���Ă݂܂�
���B
�@1�`20�̐����̔z�u�ŁA�}�̗��ɂ�4��8�̏ꍇ�̑��ɁA���ɂ̐������ǂ̂悤�Ȃ��̂���
��ł��傤���B
�@�@
�@�u�X�i���g�̕��w�v�ɂ���
�@�����w�̖{�ŁA�u���w�̌����v�i���R��,�����y���A��㋳��}���j�̒��ŁA�K�c�I����
�u���w����v�ŏЉ��Ă����A�X�i���g���̎����w�Ƃ������̂�����܂��B
(���@�u��������v���Q��)
40 39 08 34 09 25 20
03 12 47 07 45 33 28
16 42 11 22 10 48 26
31 17 15 49 13 18 32
27 41 21 04 14 44 24
35 19 37 30 46 06 02
23 05 36 29 31 01 43
�@���̕��w�ł́A�c�E���E�Ίp���̑��a�����łȂ��A���p�Ə̂��钆�S�̃}�X�Œ��p�ɐ܂��
����7�}�X(��:34,7,22,49,15,17,31�A����сA40,12,11,49,21,19,23)�A�s�p�Ə̂���45�x�Ő܂��
����7�}�X(��:40,12,11,49,15,17,31)�A
�݊p�Ə̂���135�x�Ő܂�Ȃ���7�}�X(��:34,7,22,49,21,19,23)�̑��a���������A����ɁA���S��
�l���̌v5�}�X�̘a�A���S�Ǝl�ӂ̒����̌v5�}�X�̘a���������Ȃ��Ă���Ƃ������̂ł����B
�@�u���w�̌����v�ł͒��S�̃}�X��47�̏ꍇ�����邱�Ƃ��ł��������ł����A45�̏ꍇ�͂�
���Ă��Ȃ������ł��B
�@�X�i���g���̕��w���ܕ��w�ɂ���ƁA�Ⴆ�A
10 04 25 09 17
05 22 07 15 16
08 24 01 21 11
23 13 12 14 03
19 02 20 06 18
�Ƃ������̂�����܂����A���S�̃}�X��1�ȊO��3,5,7,9,11,13�̏ꍇ�͉\�ł��傤���B
�܂��A�X�i���g���̕��w������w�A�\����w�A...�Ƃ������͉̂\�ł��傤���B
�@�f�`�h ����̃R�����g�ł��B�i�ߘa�U�N�P�P���Q�S���t���j
�@�@
�@��}�ɂ����āA
20��17�@�A17��20�@�A18��19�@�A19��18
�Ɠ���ւ��Ă����v�Ǝv���܂��B
�@�炷���邳��̃R�����g�ł��B�i�ߘa�U�N�P�P���Q�S���t���j
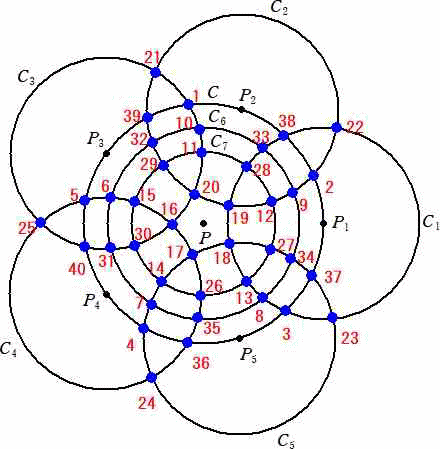
�@kuiperbelt �������ꂽ���́A���������Ă��Ȃ��C�����܂��B
C1�̉~����: 22+38+33+28+18+19+13+8+3+23 = 205
C2�̉~����: 21+39+32+29+17+18+12+9+2+22 = 201
C3�̉~����: 25+40+31+30+16+17+11+10+1+21 = 202
C4�̉~����: 24+36+35+26+20+16+15+6+5+25 = 208
C5�̉~����: 23+37+34+27+19+20+14+7+4+24 = 209
�@GAI�������ꂽ�悤�ɁA����ւ���ΑS��205�ɂȂ�܂��̂ŁA�u����ւ��Ă����v�v
�ł͂Ȃ��A�u����ւ��Ȃ��ƃ_���v���Ǝv���܂��B
�@kuiperbelt ����̃R�����g�ł��B�i�ߘa�U�N�P�P���Q�S���t���j
�@���w�E�̂Ƃ���A�]�L�~�X�������̂ŁA�������Ă����܂��B
�@�@
�@�f�`�h ����̃R�����g�ł��B�i�ߘa�U�N�P�P���Q�T���t���j
�@�@
�ɂ��āA���ɂɎ���2�̐�����z�u���Ă����A����6�g�̘a��=>�ł̒l�i���R��)�ɂ���
�c��̐��������傤��2�x���o������悤��6�g��6���̐����̑g�����͎R�قǍ\����
�\�ƂȂ�Ǝv���܂��B
1;1,2=>69�@�A2;1,5=>68�@�A3;1,8=>67�@�A4;1,11=>66�@�A5;1,14=>65�@�A6;1,17=>64�@�A7;1,20=>63
8;2,4=>68�@�A9;2,7=>67�@�A10;2,10=>66�@�A11;2,13=>65�@�A12;2,16=>64�@�A13;2,19=>63
14;3,6=>67�@�A15;3,9=>66�@�A16;3,12=>65�@�A17;3,15=>64�@�A18;3,18=>63�@�A19;4,5=>67
20;4,8=>66 (��}�̃p�^�[��)�@�A21;4,11=>65�@�A22;4,14=>64�@�A23;4,17=>63�@�A24;4,20=>62
25;5,7=>66�@�A26;5,10=>65�@�A27;5,13=>64�@�A28;5,16=>63�@�A29;5,19=>62�@�A30;6,9=>65
31;6,12=>64�@�A32;6,15=>63�@�A33;6,18=>62�@�A34;7,8=>65�@�A35;7,11=>64�@�A36;7,14=>63
37;7,17=>62�@�A38;7,20=>61�@�A39;8,10=>64�@�A40;8,13=>63�@�A41;8,16=>62�@�A42;8,19=>61
43;9,12=>63�@�A44;9,15=>62�@�A45;9,18=>61�@�A46;10,11=>63�@�A47;10,14=>62�@�A48;10,17=>61
49;10,20=>60�@�A50;11,13=>62�@�A51;11,16=>61�@�A52;11,19=>60�@�A53;12,15=>61�@�A54;12,18=>60
55;13,14=>61�@�A56;13,17=>60�@�A57;13,20=>59�@�A58;14,16=>60�@�A59;14,19=>59�@�A60;15,18=>59
61;16,17=>59�@�A62;16,20=>58�@�A63;17,19=>58�@�A64;19,20=>57
�@kuiperbelt ����̃R�����g�ł��B�i�ߘa�U�N�P�Q���P���t���j
�@GAI ����́u���~���w�v�́A3�̓��S�~��5�̉~����������悤�ɁA���A5�̉~�̂���
�ׂ荇��2�̉~����������悤�ɔz�u�����Ƃ��ɂł���40�̌�_�ɁA1�`40�̐����A2��
�~�̌�_�ł���2�_�ɘa��41�ƂȂ�悤�ɔz�u����ƁA�~���10�_�̑��a��205�̒�a�ƂȂ�
�Ƃ������̂ł����B
�@�������ʉ����āAn�̓��S�~��(n+2)�̉~����������悤�ɁA���A(n+2)�̉~�̂���
�ׂ荇��2�̉~����������悤�ɔz�u�����Ƃ��ɂł���2(n+1)(n+2)�̌�_�ɁA1�`2(n+1)(n+2)
�̐����A2�̉~�̌�_�ł���2�_�ɘa��2(n+1)(n+2)+1�ƂȂ�悤�ɔz�u����ƁA�~���2(n+2)
�_�̑��a��(n+2)(2(n+1)(n+2)+1)�̒�a�ƂȂ�Ƃ���(2n+2)�~�w���l���Ă݂܂����B
�@n=1�̏ꍇ�́A4�~�w�ŁA1�̉~��3�̉~����������悤�ɁA���A3�̉~�̂����ׂ荇
��2�̉~����������悤�ɔz�u�����Ƃ��ɂł���12�̌�_�ɁA1�`12�̐����A2�̉~�̌�
�_�ł���2�_�ɘa��13�ƂȂ�悤�ɔz�u����ƁA�~���6�_�̑��a��39�̒�a�ƂȂ�Ƃ�������
�ŁA�u�����w�̐��E(��X����)�v��p.274�̉E����4�~�w�ŁA�~�̑召�W���������̂ɑ�
�����܂��B
�@n=2�̏ꍇ�́A6�~�w�ŁA2�̓��S�~��4�̉~����������悤�ɁA���A4�̉~�̂���
�ׂ荇��2�̉~����������悤�ɔz�u�����Ƃ��ɂł���24�̌�_�ɁA1�`24�̐����A2��
�~�̌�_�ł���2�_�ɘa��25�ƂȂ�悤�ɔz�u����ƁA�~���8�_�̑��a��100�̒�a�ƂȂ�
�Ƃ������̂ŁA�u�����w�̐��E(��X����)�v��p.275�̍�����6�~�w�ʼn~�̑召�W����
�����̂ɑ������܂��B
�@n=3�̏ꍇ��8�~�w���AGAI ����́u���~���w�v�ƂȂ�܂��B
�@n=4�̏ꍇ�́A10�~�w�ŁA4�̓��S�~��6�̉~����������悤�ɁA���A6�̉~�̂���
�ׂ荇��2�̉~����������悤�ɔz�u�����Ƃ��ɂł���60�̌�_�ɁA1�`61�̐����A2��
�~�̌�_�ł���2�_�ɘa��61�ƂȂ�悤�ɔz�u����ƁA�~���12�_�̑��a��366�̒�a�ƂȂ�
�Ƃ������̂ł��B
�@�@
4�~�w
�@�@
6�~�w
�@�@
�@kuiperbelt ����̃R�����g�ł��B�i�ߘa�U�N�P�Q���V���t���j
�@n^2�̑f�� p_{1},p_{2},...,p_{n^2} ����Ȃ�f�������w�ƁA���̑o�q�f�� p_{1}+2,p_{2}+2,...,p_{n^2}+2
����Ȃ�f�������w�Ƃ������n���̖����w������Ƃ��܂��B�i���@�Q�l�j
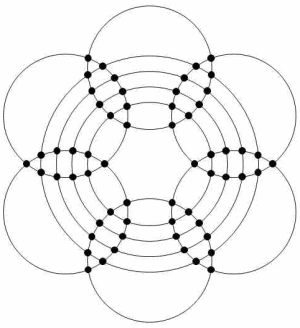
�@���̂悤�Ȉ��n���̑f�������w����An��n�a�̑f�����~�w�����邱�Ƃ��ł��܂��B
�}��3���̑f�������w���������3��3�a�̑f�����~�w�ł��B
�@�ʏ�̖����w�Ɠ��l�ɑf�������w�ł�2���̖����w�����邱�Ƃ͂ł��܂��A�o�q�f��
���g����2��2�a�̑f�����~�w�����邱�Ƃ��ł��܂��B
�@4�g�̑o�q�f���� p1,p1+2,p2,p2+2,p3,p3+3,p4,p4+2 �Ƃ��āAp1+p4=p2+p3 �̊W�����藧��
�Ƃ��ɁAp1,p2,p3,p4 �ƑΏ̂Ȉʒu�� p4+2,p3+2,p2+2,p1+2 �Ɣz�u����ƁA���a�ƌa�a����a��
�Ȃ�܂��B
�@�O�q�f���ɂ� p,p+2,p+6 �̃^�C�v�� p,p+4,p+6 �̃^�C�v������܂����A3�g�̎O�q�f��
p1,p1+2,p1+6,p2,p2+2,p2+6,p3,p3+2,p3+6 ��
p1+2,p3+6,p2
p3,p2+2,p1+6
p2+6,p1,p3+2
�Ɣz��ƁA�c�Ɖ���������a p1+p2+p3+8 ��3�~3���w�ƂȂ�܂��B
�@�܂��A3�g�̎O�q�f�� p1,p1+4,p1+6,p2,p2+4,p2+6,p3,p3+4,p3+6 ��
p1+4,p3+6,p2
p3,p2+4,p1+6
p2+6,p1,p3+4
�Ɣz��ƁA�c�Ɖ���������a p1+p2+p3+10 ��3�~3���w�ƂȂ�܂��B���̂悤��3�~3���w
��2�g���āA3��3�a�̑f�����~�w�����邱�Ƃ��ł��܂��B
�@�@
�@4���̑f�������w���������4��4�a�̑f�����~�w
�@�@
�@�o�q�f����2��2�a�̑f�����~�w
�@�@
�@�O�q�f����3��3�a�̑f�����~�w
�@�@
�@kuiperbelt ����̃R�����g�ł��B�i�ߘa�U�N�P�Q���Q�Q���t���j
�@(2k+1)^2���̓�d�����w�ɂ��āA��d�����w�Ƃ����āA�e�i�̐��̏c�E���E�Ίp���̘a��
��a�ɂȂ邾���łȂ��A�e�i�̐��̏c�E���E�Ίp���̓��a����a�ɂȂ閂���w������܂��B
�@9���̓�d�����w�̍����ŁA0�`8�̎��R�z��Ȃ�3�~3�s��A�ƁA0�`8����Ȃ�c�E��
�E�Ίp���̘a����a12��3���̖����w�ƂȂ�s��B������Ƃ��܂��B
A=
[0 1 2]
[3 4 5]
[6 7 8]
B=
[7 2 3]
[0 4 8]
[5 6 1]
���̂悤��3�~3�s��A,B�ƁA
S=
[0 1 0]
[0 0 1]
[1 0 0]
�Ƃ���3�~3�s��S��p���āA�s��A�AB�̍s�������ւ����s�玟�̂悤�� 9�~9 �s��
���A��������ƁA9��+��+E (E�͑S�v�f��1�̍s��)�́A9 ���̓�d�����w�ƂȂ�܂��B
��=
[S^2*A*S^2, A*S^2, S*A*S^2]
[ S^2*A, A, S*A]
[ S^2*A*S, A*S, S*A*S]
��=
[ S*B*S, B*S, S^2*B*S]
[ S*B, B, S^2*B]
[S*B*S^2, B*S^2, S^2*B*S^2]
9��+��+E=
[72 73 59 13 26 3 38 51 34]
[11 24 7 45 46 32 67 80 57]
[40 53 30 65 78 61 18 19 5]
[55 68 81 8 12 22 33 43 47]
[ 6 16 20 28 41 54 62 66 76]
[35 39 49 60 70 74 1 14 27]
[77 63 64 21 4 17 52 29 42]
[25 2 15 50 36 37 75 58 71]
[48 31 44 79 56 69 23 9 10]
���l�ɁA���̂悤�� 0�`24 �̎��R�z��Ȃ� 5�~5 �s��A�ƁA0�`24 ����Ȃ�c�E���E�Ίp
���̘a����a 60 �� 5 ���̖����w�ƂȂ�s��B�ƁA5�~5 �s��S��p���āA�s��A�AB�̍s��
������ւ����s�玟�̂悤��25�~25�s�A��������ƁA25��+��+E(E�͑S�v�f��
1�̍s��)�́A25 ���̓�d�����w�ƂȂ�܂��B
A=
[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]
[15 16 17 18 19]
[20 21 22 23 24]
B=
[16 22 3 9 10]
[23 4 5 11 17]
[ 0 6 12 18 24]
[ 7 13 19 20 1]
[14 15 21 2 8]
S=
[0 1 0 0 0]
[0 0 1 0 0]
[0 0 0 1 0]
[0 0 0 0 1]
[1 0 0 0 0]
��=
[S^3*A*S^3, S^4*A*S^3, A*S^3, S*A*S^3, S^2*A*S^3]
[S^3*A*S^4, S^4*A*S^4, A*S^4, S*A*S^4, S^2*A*S^4]
[ S^3*A, S^4*A, A, S*A, S^2*A]
[ S^3*A*S, S^4*A*S, A*S, S*A*S, S^2*A*S]
[S^3*A*S^2, S^4*A*S^2, A*S^2, S*A*S^2, S^2*A*S^2]
��=
[S^2*B*S^2, S*B*S^2, B*S^2, S^4*B*S^2, S^3*B*S^2]
[ S^2*B*S, S*B*S, B*S, S^4*B*S, S^3*B*S]
[ S^2*B, S*B, B, S^4*B, S^3*B]
[S^2*B*S^4, S*B*S^4, B*S^4, S^4*B*S^4, S^3*B*S^4]
[S^2*B*S^3, S*B*S^3, B*S^3, S^4*B*S^3, S^3*B*S^3]
�@25���̓�d�����w�ɂ��ẮA���������Q�ƁB
�@���l�ɁA���̂悤�� 0�`48 �̎��R�z��Ȃ� 7�~7 �s��A�ƁA0�`48 ����Ȃ�c�E���E��
�p���̘a����a 168 �� 7 ���̖����w�ƂȂ�s��B�ƁA7�~7 �s��S��p���āA�s��A�AB��
�s�������ւ����s��A���̂悤�� 49�~49 �s�A��������� 49��+��+E (E��
�S�v�f��1�̍s��)�́A49 ���̓�d�����w�ƂȂ�܂��B
A=
[ 0 1 2 3 4 5 6]
[ 7 8 9 0 11 12 13]
[14 15 16 17 18 19 20]
[21 22 23 24 25 26 27]
[28 29 30 31 32 33 34]
[35 36 37 38 39 40 41]
[42 43 44 45 46 47 48]
B=
[29 37 45 4 12 20 21]
[38 46 5 13 14 22 30]
[47 6 7 15 23 31 39]
[ 0 8 16 24 32 40 48]
[ 9 17 25 33 41 42 1]
[18 26 34 35 43 2 10]
[27 28 36 44 3 11 19]
S=
[0 1 0 0 0 0 0]
[0 0 1 0 0 0 0]
[0 0 0 1 0 0 0]
[0 0 0 0 1 0 0]
[0 0 0 0 0 1 0]
[0 0 0 0 0 0 1]
[1 0 0 0 0 0 0]
��=
[S^4*A*S^4, S^5*A*S^4, S^6*A*S^4, A*S^4, S*A*S^4, S^2*A*S^4, S^3*A*S^4]
[S^4*A*S^5, S^5*A*S^5, S^6*A*S^5, A*S^5, S*A*S^5, S^2*A*S^5, S^3*A*S^5]
[S^4*A*S^6, S^5*A*S^6, S^6*A*S^6, A*S^6, S*A*S^6, S^2*A*S^6, S^3*A*S^6]
[ S^4*A, S^5*A, S^6*A, A, S*A, S^2*A, S^3*A]
[ S^4*A*S, S^5*A*S, S^6*A*S, A*S, S*A*S, S^2*A*S, S^3*A*S]
[S^4*A*S^2, S^5*A*S^2, S^6*A*S^2, A*S^2, S*A*S^2, S^2*A*S^2, S^3*A*S^2]
[S^4*A*S^3, S^5*A*S^3, S^6*A*S^3, A*S^3, S*A*S^3, S^2*A*S^3, S^3*A*S^3]
��=
[S^3*B*S^3, S^2*B*S^3, S*B*S^3, B*S^3, S^6*B*S^3, S^5*B*S^3, S^4*B*S^3]
[S^3*B*S^2, S^2*B*S^2, S*B*S^2, B*S^2, S^6*B*S^2, S^5*B*S^2, S^4*B*S^2]
[ S^3*B*S, S^2*B*S, S*B*S, B*S, S^6*B*S, S^5*B*S, S^4*B*S]
[ S^3*B, S^2*B, S*B, B, S^6*B, S^5*B, S^4*B]
[S^3*B*S^6, S^2*B*S^6, S*B*S^6, B*S^6, S^6*B*S^6, S^5*B*S^6, S^4*B*S^6]
[S^3*B*S^5, S^2*B*S^5, S*B*S^5, B*S^5, S^6*B*S^5, S^5*B*S^5, S^4*B*S^5]
[S^3*B*S^4, S^2*B*S^4, S*B*S^4, B*S^4, S^6*B*S^4, S^5*B*S^4, S^4*B*S^4]
�@49 ���̓�d�����w�ɂ��ẮA���������Q�ƁB
�@Dengan kesaktian Indukmu ����̃R�����g�ł��B�i�ߘa�U�N�P�Q���Q�Q���t���j
�@�X���̓�d�����w�ɂ����āA�ӂ�����Ίp���́y�����a�z���������Ȃ��Ă���̂ł��ˁB
����ł��ˁB
�@�@�ȉ��A�H�����I







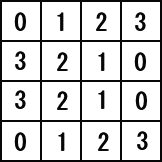
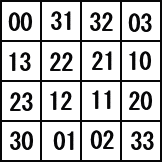







 �@�@
�@�@
 �@
�@

















