ブール代数　　　　　　　　 　　　　　　　　　　　　　　　　　　　

　数学において、集合や命題を考えるとき、両者には実は同一の性質・法則が成り立ってい
ることに気がつく。

例　ド・モルガンの法則によれば、２つの集合 Ａ，Ｂ に対して、

　　　　　　　　　　　　　　　　 　

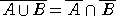
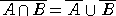
が成り立つ。このことと同様の事実が、２つの命題 ｐ，ｑ についても、成り立つ。

　　　 ¬（ｐ∨ｑ）＝（¬ｐ）∧（¬ｑ）　　　¬（ｐ∧ｑ）＝（¬ｐ）∨（¬ｑ）

　この事実もまた、ド・モルガンの法則と呼ばれる。（参考：数学の論理）

　ブール（Ｂｏｏｌｅ　1815〜1864）は、このような類似性を一般化して、次のようなブール代数を
考案した。

　集合 Ｂ には、異なる２つの要素 ０、１ が含まれ、さらに、ａ＋ｂ ， ａ＊ｂ ，ａ’ のような演算
が定義されているものとする。
　任意の ａ、ｂ、ｃ ∈ Ｂ に対して、次の法則が成り立つとき、Ｂ は、ブール代数と呼ばれる。
（１）・・・交換律　　　ａ＋ｂ＝ｂ＋ａ　　　ａ＊ｂ＝ｂ＊ａ
（２）・・・分配律　　　ａ＋（ｂ＊ｃ）＝（ａ＋ｂ）＊（ａ＋ｃ）　　　ａ＊（ｂ＋ｃ）＝（ａ＊ｂ）＋（ａ＊ｃ）
（３）・・・同一律　　　ａ＋０＝ａ　　　　　 ａ＊１＝ａ
（４）・・・補元律　　　ａ＋ａ’＝１　　　　 ａ＊ａ’＝０

（注）　２つの要素 ０、１ は、普通それぞれ、最小元、最大元と呼ばれる。また、＋は和、＊は
　　　積にそれぞれ相当するが、差や商に相当するものはない。

ブール代数の代表的な例　　　Ｂ＝｛０、１｝ とし、演算を次のように定義する。

　このとき、Ｂ は、ブール代数になる。

これは、デジタル計算機の内部で行われている演算そのものである。

　ところで、「１」を、命題が真であること、「０」を、命題が偽であることと読みかえれば、上の
演算表は、
　　　　　　　　「＋」という演算は、「または」を、
　　　　　　　　「＊」という演算は、「かつ」を、
　　　　　　　　「’」という演算は、「〜でない」という論理を表していると解釈することもできる。

　このブール代数は、推理問題を手際よく解く方法として利用される。

例　今、１つの事柄について、２つの矛盾した証言があるとする。
　ある人は、「その事柄は、Ａであり、Ｂである。」といい、
また、別な人は、「その事柄は、Ｂであり、Ｃである。」といった。
２人とも１つは正しいことをいい、１つは間違ったことをいっているものとする。

　このとき、明らかに、Ｂが正しい事柄であるが、ブール代数を用いると、次のような機械的
な計算で、「正しい事柄はＢである」ということが分かる。

　条件から、Ａ＊Ｂ＝０、Ｂ＊Ｃ＝０、Ａ＊Ｃ＝０ である。また、Ａ＋Ｂ＝１、Ｂ＋Ｃ＝１ なので、
（Ａ＋Ｂ)＊(Ｂ＋Ｃ）＝１ が成り立つ。交換律と分配律と同一律を用いて、
（Ａ＋Ｂ)＊(Ｂ＋Ｃ）＝（Ｂ＋Ａ)＊(Ｂ＋Ｃ）＝Ｂ＋Ａ＊Ｃ＝Ｂ＋０＝Ｂ なので、Ｂ＝１ となる。
　したがって、Ｂが正しい事柄である。

　上記の例は、ブール代数の使い方を例示するものとして、自明な場合を想定したが、次の
場合はどうだろうか？多分、「エッ？」という人が多いのではないかと思う。これに対しても、
ブール代数の知識があれば、鮮やかに問題を解決することができる。

例　ある人物について、Ａ、Ｂ、Ｃ の３人は、次のように証言した。
　　Ａ：「たしか、名前は、大場さんといい、年は、３５歳」
　　Ｂ：「たしか、名前は、小塚さんといい、年は、３０歳」
　　Ｃ：「たしか、名前は、大場さんではなく、年は、４０歳」
３人とも、名前、年齢のどちらかは正しいことをいい、どちらかは間違ったことを言っているも
のとする。さて、ある人物の名前と年齢は、なんであろうか？

（解）　ａ＝「名前は、大場さん」、ｂ＝「名前は、小塚さん」、ｃ＝「名前は、大場さんでない」
　　　　ｄ＝「年齢は、３５歳」、ｅ＝「年齢は、３０歳」、ｆ＝「年齢は、４０歳」　とすると、
　　題意より、次の各式が成り立つ。
　　　　ａ＊ｄ＝０、ｂ＊ｅ＝０、ｃ＊ｆ＝０
　　　　ａ＋ｄ＝１、ｂ＋ｅ＝１、ｃ＋ｆ＝１
　　　　ａ＊ｂ＝０、ａ＊ｃ＝０、ｄ＊ｅ＝０、ｅ＊ｆ＝０、ｄ＊ｆ＝０
　　このとき、
　　　　（ａ＋ｄ)＊(ｂ＋ｅ）＝（（ａ＋ｄ)＊ｂ）＋（（ａ＋ｄ)＊ｅ）
　　　　　　　　　　　　　　 ＝（ａ＊ｂ）＋（ｂ＊ｄ）＋（ａ＊ｅ）＋（ｄ＊ｅ）
　　　　　　　　　　　　　　 ＝０＋（ｂ＊ｄ）＋（ａ＊ｅ）＋０
　　　　　　　　　　　　　　 ＝（ｂ＊ｄ）＋（ａ＊ｅ）
　　であるので、
　　　　　　　　　　（ｂ＊ｄ）＋（ａ＊ｅ）＝１
　　が成り立つ。
　　　よって、さらに、
　　　　（ｃ＋ｆ）＊（（ｂ＊ｄ）＋（ａ＊ｅ））＝（（ｃ＋ｆ）＊（ｂ＊ｄ））＋（（ｃ＋ｆ）＊（ａ＊ｅ））
　　　　　　　　　　　　　　　　　　　　　　＝（ｂ＊ｃ＊ｄ）＋（ｂ＊ｄ＊ｆ）＋（ａ＊ｃ＊ｅ）＋（ａ＊ｅ＊ｆ）
　　　　　　　　　　　　　　　　　　　　　　＝（ｂ＊ｃ＊ｄ）＋（ｂ＊０）＋（０＊ｅ）＋（ａ＊０）
　　　　　　　　　　　　　　　　　　　　　　＝（ｂ＊ｃ＊ｄ）＋０＋０＋０
　　　　　　　　　　　　　　　　　　　　　　＝ｂ＊ｃ＊ｄ
　 であるので、
　　　　　　　　　　　ｂ＊ｃ＊ｄ＝１
　　が成り立つ。
　　　したがって、ｂ、ｃ、ｄ が、正しい事柄であることが分かり、

　　ある人物の名前は、「小塚さん」であり、年齢は、「３５歳」ということになる。

　このように、ブール代数は、ちょっと見た目にはすごく複雑に見えるような問題を解くのに役
立つ。

（参考文献：Ｓｅｙｍｏｕｒ　Ｌｉｐｓｃｈｕｔｚ　著　成嶋　弘　監訳　離散数学　（オーム社）
　　　　　　　 Ｊ．Ａ．Ｈ．ハンター　Ｊ．Ｓ．マダチー　著　田中　勇　訳
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　数学レクリエーション（白揚社））