数学の論理 
数学の問題を解くとき、「正攻法でやると多少めんどうになりそうだな〜」と感じるときがある。
そんなとき、問題を同値な、そして考えやすい別な問題にすり替えることは、問題解決の常套
手段である。このページでは、その基本的な方策について、まとめてみたい。
いくつかの予備知識を確認しながら、話を進める。
命題について
客観的に、真偽が判定できるような数式・文章を命題という。
(例) 1+1=2 ・・・ 命題で、真
日本の人口は、1億である ・・・ 命題で、偽
あなたは、数学が好きですか? ・・・ 真偽判定不能で、命題とならない
いくつかの命題から、別な命題を作ることを、命題の合成という。
次の、3つのタイプが基本的である。命題 P、Q に対して、
(離接) P または Q 記号では、P∨Q と書く。
(合接) P かつ Q 記号では、P∧Q と書く。
(否定) P でない 記号では、¬P または、 〜P または、 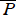 と書く。
と書く。
(例) 2つの命題 P: X<2 、Q: X>0 に対して、
P∨Q : Xは、全ての実数 、P∧Q : 0<X<2 、¬P : X≧2
命題の真理表について
命題 P、Q の真偽によって、合成命題 P∨Q、P∧Q、¬P の真偽が次の表に従って定め
られる。表において、真は 「1」、偽は 「0」で表される。
| P |
Q |
P∨Q |
P∧Q |
¬P |
| 1 |
1 |
1 |
1 |
0 |
| 1 |
0 |
1 |
0 |
0 |
| 0 |
1 |
1 |
0 |
1 |
| 0 |
0 |
0 |
0 |
1 |
|
左の表によって定められた真理表は、日常
の感覚と大体同じなので、違和感なく覚えられ
ることと思う。ただ、「または」は、日常使ってい
る感覚(排他的)と異なるので、注意を要する。
|
日常で、「ハンバーガーまたはジュースを頼む」と言われたら、どちらか一方を頼むのが普
通だが、数学では、両方頼むことも有りとなる。
#「∨」は、ラテン語の vel (どちらか少なくとも一方)からとられたらしい。日常使っている排
他的な「または」としては、別な単語 aut を使うようだ。
(参考文献:足立恒夫 著 数 体系と歴史 (朝倉書店))
(例) ¬P∨Q の真理表を作れ。
| P |
¬P |
Q |
¬P∨Q |
| 1 |
0 |
1 |
1 |
| 1 |
0 |
0 |
0 |
| 0 |
1 |
1 |
1 |
| 0 |
1 |
0 |
1 |
真理値が全て、0(偽)である命題を、矛盾命題といい、真理値が全て、1(真)である命題
をトートロジーという。
また、2つの命題の真理表が全く同一のとき、これらの命題は、論理的に同値であるとい
い、等号を用いて表される。
(論理的に同値な命題の例)
1.(2重否定) ¬(¬P)=P (Pでないことはないは、Pそのものということ)
2.(ド・モルガンの法則)
¬(P∨Q)=(¬P)∧(¬Q) (またはの否定は、かつ)
¬(P∧Q)=(¬P)∨(¬Q) (かつの否定は、または)
3.(分配の法則)
P∧(Q∨R)=(P∧Q)∨(P∧R) 、P∨(Q∧R)=(P∨Q)∧(P∨R)
条件命題について
数学では、「P ならば Q である」という形式の命題が多い。記号で、P → Q と書く。この
命題も、合成命題の一つであり、次のように、真理表が定められる。
| P |
Q |
P → Q |
| 1 |
1 |
1 |
| 1 |
0 |
0 |
| 0 |
1 |
1 |
| 0 |
0 |
1 |
|
この真理表と、先の(例)における ¬P∨Q の真理
表を比較して分かるように、両者は、論理的に同値で
ある。すなわち、
P → Q = ¬P∨Q が成り立つ。 |
(覚え方としては、「PかつQでない、ことはない」の方がいいかもしれない。私自身は、そう
覚えている。)
(参考) 両者が論理的に同値であることに違和感を抱く人は多い。次のように考えてはどう
だろうか。
「P ならば Q である」の否定が、「P であるのに Q でない」と理解できれば、それは、暗
黙のうちに、¬(P → Q) = P∧¬Q すなわち、P → Q = ¬P∨Q ということを認めざ
るをえないということである。(参考文献:足立恒夫 著 数 体系と歴史 (朝倉書店))
この命題で大切なポイントは、仮定Pが偽ならば、結論Qの真偽に関わらず、P
→ Q が
真になるところである。
「雨が降れば、傘を差す」という行為について、雨が降っているのに傘を差さないのは、変
であるが、雨が降らなければ、傘を差しても差さなくても変ではない。お天気なのに、傘を差
していることを咎められたら、「これは、日傘です。」とでも言っておけばよい。
同様に、「明日天気がよければ外出しよう」と約束したら、天気が悪いときは、外出しても、
しなくても自由で、約束を破ったことにはならない。天気がよいのに外出しなかったら、それ
は、約束を破ったことになる。
この場合の応用例として、次の問題は有名である。
(例) 空集合は、すべての集合の部分集合である。
B⊂A であるとき、BはAの部分集合である。ところで、B⊂A とは、「X∈B ならば、
X∈A」が成り立つことをいう。いま、Bが空集合のとき、X∈Bは偽なので、命題「X∈B なら
ば、X∈A」は真である。よって、空集合Bは、任意の集合Aの部分集合である。
このように、仮定が偽のとき、命題 P → Q は、無内容的に成り立つという。
(参考) 「偽」の命題からは、どんな命題も導けるといった、ラッセルの講演の話が知られ
ている。
例えば、「2=1」の命題から、「私は、日本の総理大臣」という命題は、次のように証明さ
れる。
「2≠1」は、「真」の命題なので、「2≠1」∨「私は、日本の総理大臣」は、「真」の命題
ところで、「2=1」の命題が成り立つと仮定するということは、「2=1」が「真」の命題、すなわ
ち、「2≠1」は、「偽」の命題と仮定するということである。
「2≠1」∨「私は、日本の総理大臣」は、「真」の命題であったので、「私は、日本の総理大
臣」が「真」の命題ということになる。したがって、「2=1」ならば、「私は、日本の総理大臣」
である。(参考文献:足立恒夫 著 数 体系と歴史 (朝倉書店))
(例) 三段論法がトートロジーであることを示せ。
| P |
Q |
R |
P → Q |
Q → R |
P → R |
(P→Q)∧(Q→R) |
(P→Q)∧(Q→R)→(P→R) |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
| 1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
| 1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
| 0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
| 0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
| 0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
このことから、三段論法(P ならば、Q で Q ならば、R のとき、P ならば R)による推論
は、常に有効である。
(例) アリバイの原理がトートロジーであることを示せ。
| P |
Q |
P → Q |
¬P |
¬Q |
(P → Q)∧(¬Q) |
(P → Q)∧(¬Q) → (¬P) |
| 1 |
1 |
1 |
0 |
0 |
0 |
1 |
| 1 |
0 |
0 |
0 |
1 |
0 |
1 |
| 0 |
1 |
1 |
1 |
0 |
0 |
1 |
| 0 |
0 |
1 |
1 |
1 |
1 |
1 |
このことから、「P ならば Q だが、Q でなければ、P でない」という推論は常に有効である。
よおすけさんからのコメントです。(令和5年7月23日付け)
命題((P→Q)∧(Q→R))→(P→R) がトートロジーであることの別証明です。
(証明) 命題((P→Q)∧(Q→R))→(P→R) が偽となるのは、
P→Q が真、Q→R が真、P→R が偽の場合だけである。
ところで、P→R が偽となるのは、Pが真で、Rが偽の場合だけである。
Pが真で、P→Q が真より、Qが真となり、Q→R が真より、Rが真となるが、Rが偽であるこ
とに矛盾する。
したがって、この命題が偽となることは無く、トートロジーである。 (証終)
必要条件と十分条件
命題 P → Q が常に真であるとき、記号 P ⇒ Q で表す。
このとき、Pは、Qであるための十分条件といい、Qは、Pであるための必要条件であると
いう。
(例) X=1 ⇒ X2=1 において、
「X=1」は、「X2=1」であるための十分条件
・・・X2=1であるためには、X=1であれば十分!
「X2=1」は、「X=1」であるための必要条件
・・・X=1であるためには、とりあえず X2=1であることが必要!
逆・裏・対偶
命題 P → Q に対して、次の命題を、それぞれ、もとの命題の逆、裏、対偶という。
逆 : Q → P
裏 : ¬P → ¬Q
対偶 : ¬Q → ¬P
(例) もとの命題とその対偶は、論理的に同値であることを示せ。
| P |
Q |
P → Q |
¬Q |
¬P |
¬Q → ¬P |
| 1 |
1 |
1 |
0 |
0 |
1 |
| 1 |
0 |
0 |
1 |
0 |
0 |
| 0 |
1 |
1 |
0 |
1 |
1 |
| 0 |
0 |
1 |
1 |
1 |
1 |
このことから、ある命題を証明するかわりに、その対偶を証明してもよいことになる。しか
も、問題によっては、対偶を証明する方が、非常に楽な場合がある。これは、経験的に、確
かな真実である。
(例) 3つの数 X、Y、Z について、X+Y+Z>3 ならば、少なくとも一つは、1
より大きい。
この命題の対偶は、「3つの数 X、Y、Z について、どれも1以下ならば、X+Y+Z≦3」
明らかに、X≦1、Y≦1、Z≦1 ならば、X+Y+Z≦1+1+1=3 なので、対偶命題は真。
よって、もとの命題も真である。
命題関数
集合 U 上で定義された命題 P(X) を考える。命題 P(X) が真となるような集合
Uの要素 X
の集合を、命題関数 P(X) の真理集合といい、Pで表す。
それぞれの命題関数の真理集合は次のようになる。
P(X)∨Q(X) ・・・ P∪Q (PとQの結び(和集合))
P(X)∧Q(X) ・・・ P∩Q (PとQの共通部分)
¬P(X) ・・・ Pc (Pの補集合)
P(X) → Q(X) ・・・ Pc∪Q
この真理集合の考えを用いると、P ⇒ Q の証明は視覚的に行うことができる。すなわち、
P(X) ⇒ Q(X) を証明するには、P⊂Q であることを確かめればよい。
実際に、P(X) → Q(X) の真理集合は、Pc∪Q であり、命題がトートロジーであることから
Pc∪Q=U に等しい。このとき、
P=P∩U=P∩(Pc∪Q)=(P∩Pc)∪(P∩Q)=P∩Q⊂Q から、P⊂Q
逆に、P⊂Q とすると、U=Pc∪P⊂Pc∪Q⊂U から、 Pc∪Q=U
よって、命題 P(X) → Q(X) は、トートロジーである。
(例) |X|+|Y|<1 ならば、X2+Y2<1 であることを証明せよ。
この問題は、真理集合を調べることにより、簡単に示される。
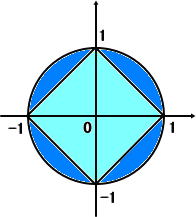 |
左図より、正方形の内部:|X|+|Y|<1 は、
円の内部:X2+Y2<1 に含まれるので、
命題は成り立つ。
|
反例の作り方
命題 P(X) → Q(X) が偽であることを示すには、反例をあげるのが手っ取り早い方法であ
る。P⊂Q が成り立たないことから、P(X)であるが、Q(X)でないようなXを一つ探せばよい。
(例) 命題「X2=1 ならば X=1」は偽である。なぜなら、X=−1という反例があるから。
全称命題と存在命題
数学において、「すべての〜」とか「〜であるものが存在する」という形式の命題は数多い。
「すべてのXに対して、P(X)である」という命題を全称命題といい、記号で、∀X:P(X) と
書く。
全称命題の真理集合は、全体集合Uである。(∀:全称記号(universal quantifier))
「あるXに対して、P(X)である」という命題を存在命題といい、記号で、∃X:P(X) と書く。
存在命題の真理集合は、空でない集合である。(∃:存在記号(existential quantifier))
(例) すべての実数Xに対して、X2≧0
ある実数Xに対して、2X−4=0
a≦b は、存在命題 ∃X≧0 : a+X=b で表される。
全称命題と存在命題について、次の関係式は基本的である。
¬(∀X:P(X))=∃X:¬P(X) (「すべて」の否定は「ある」)
¬(∃X:P(X))=∀X:¬P(X) (「ある」の否定は「すべて」)
複雑な命題を考えるとき、文章で与えられたままでは頭が混乱するので、記号化して考え
た方がよい。単純作業で、いろいろな命題に変換できる。
(例) 命題「すべての実数Xについて、X2>1 ならば、X>1 である。」の否定命題を作り、
その真偽を判定せよ。
¬(∀X:(X2>1→X>1))
=∃X:¬(X2>1→X>1)
=∃X:¬(¬(X2>1)∨(X>1))
=∃X:(X2>1)∧(X≦1)
これを、翻訳すれば、「X2>1 かつ X≦1 となる実数Xがある。」となる。
たとえば、X=−2 が該当するので、この命題は、真である。
(よって、もとの命題は偽ということになる。)
(例) 命題「P ならば、QまたはR」は、命題「Pかつ(Qでない) ならば、R」と論理的
に同値である。
実際に、P → Q∨R =(¬P)∨(Q∨R)=((¬P)∨Q)∨R
=((¬P)∨(¬(¬Q)))∨R=(¬(P∧(¬Q))∨R=P∧(¬Q) → R
これを、「XY=0 ならば、X=0 または Y=0 」に適用してみると、
「XY=0 かつ X≠0 ならば Y=0 」という形になり、納得されやすい表現になる。
この(例)における言い換えは、大学入試でよく用いられる技法で、知っている者だけが
非常に有利になる魔法の論理である。
(参考文献:茂木 勇 著 集合と論証(科学新興社)
秋山 仁 著 真理表(数学ライブラリー))
平成27年度入試 東京大学前期文系で真偽を問う問題が出題された。
問題 以下の命題A、Bそれぞれに対し、その真偽を述べよ。また、真ならば証明を与え、偽
ならば反例を与えよ。
命題A nが正の整数ならば、n3/26+100≧n2が成り立つ。
命題B 整数n、m、p が5n+5m+3p=1を満たすならば、10nm+3mp+3np<0が成
り立つ。
グラフ描画ソフトにお助けいただくと、F(x)=x3/26+100−x2 のグラフは下図の通り。
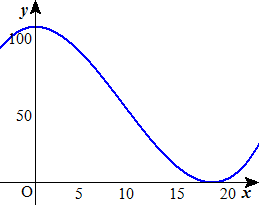 15<x<20 の周辺が微妙で、ズームして見ると、
15<x<20 の周辺が微妙で、ズームして見ると、

グラフから、x=17 が怪しい!!
(確かめ) F(17)=4913/26+100−289=−0.0384616・・・
から、ほんの一瞬、x3/26+100<x2 となるので、命題Aは偽となる。反例は、n=17。
(コメント) グラフ描画ソフトを活用して「偽」を示したが、実際の試験場では微分のお世話に
なるしかないだろう。
(命題Aの解) F(x)=x3/26+100−x2 とおくと、F(x)は微分可能な3次関数である。
ここで、 F’(x)=3x2/26−2x=0 とおくと、 x=52/3=17.333・・・で極小かつ最小
F(17)=173/26+100−172=4913/26+100−289=−0.0384616・・・<0
よって、x=17 のとき負で、正の整数nに対して、いつも n3/26+100≧n2 が成り立
つとは限らない。したがって、命題Aは偽で、反例は、n=17。 (終)
およそ受験でともに「偽」となることはないだろうと高をくくれれば命題Bは「真」だろうと予想
がつく。
実際に、整数n、m、p が5n+5m+3p=1を満たすならば、10nm+3mp+3np<0が
成り立つ。
(証明)
10nm+3mp+3np=10nm+3p(m+n)
=10nm+(1−5(n+m))(m+n)=10nm+m+n−5(n+m)2
=m+n−5n2−5m2
ここで、 m−5m2=−5(m−1/10)2+1/20 で、
m=0 のとき、 m−5m2=0 、m=1 のとき、 m−5m2=−4
同様に、 n−5n2=−5(n−1/10)2+1/20 で、
n=0 のとき、 n−5n2=0 、n=1 のとき、 n−5n2=−4
m=0 かつ n=0 とすると、 3p=1 で、この式を満たす整数pは存在しない。
よって、m、nが同時に0になることはなく、 m+n−5n2−5m2<0 が成り立つ。
以上から、命題Bは真である。 (証終)
(追記) 令和5年7月20日付け
全国的に明日から夏休み!気分的に久しぶりに論理の問題を考えてみたくなった。
問題 命題 P、Q に対して、その合成命題 P*Q を次の真理表で定義する。
| P |
Q |
P * Q |
| 1 |
1 |
0 |
| 1 |
0 |
1 |
| 0 |
1 |
1 |
| 0 |
0 |
1 |
このとき、否定 ¬P 、離接 P∨Q 、合接 P∧Q は、「*」を用いてどのように表される
だろうか?
また、
| P |
Q |
P∨Q |
¬P |
¬Q |
(¬P)*(¬Q) |
| 1 |
1 |
1 |
0 |
0 |
1 |
| 1 |
0 |
1 |
0 |
1 |
1 |
| 0 |
1 |
1 |
1 |
0 |
1 |
| 0 |
0 |
0 |
1 |
1 |
0 |
から、 P∨Q=(¬P)*(¬Q)
よって、 P∨Q=(P * P)*(Q * Q)
さらに
| P |
Q |
P∧Q |
¬(P∧Q) |
| 1 |
1 |
1 |
0 |
| 1 |
0 |
0 |
1 |
| 0 |
1 |
0 |
1 |
| 0 |
0 |
0 |
1 |
から、 ¬(P∧Q)=P * Q なので、 P∧Q=¬(P * Q)
よって、 P∧Q=(P * Q)*(P * Q) (終)
こういう論理の問題は、数学の授業ではあまり詳しく言及されることはなく、大学の一般教
養の哲学の講義で詳しい話を聞いたような気がする。
問題 Q∧R が偽のとき、(Q → P)∨(R → P) はトートロジーであることを示せ。
トートロジーを示すには、真理表を作って、真理値が全て、1(真)であることを示せばよい
わけであるが、次のように示してもよい。
(解) (Q → P)∨(R → P)=(¬Q∨P)∨(¬R∨P)=¬(Q∧R)∨P
よって、Q∧R が偽のとき、¬(Q∧R)は真となり、Pの真偽に関わらず、¬(Q∧R)∨P
は真となるので、(Q → P)∨(R → P) はトートロジーである。 (終)
(コメント) Q∧R が偽のとき、QまたはRは偽で、そのとき、Q → P または R → P は
無内容的に成り立つから真。だから、トートロジーであることは自明かな。
問題 次の命題はトートロジーであることを示せ。
(1) (¬P)∨P
(2) (P∧Q) → (R∨P)
(3) (¬(P∧Q))∨P
(4) (P∧(¬Q)) → ((¬P) → Q)
(解)(1) (¬P)∨P の真理集合は全体集合Uなので、トートロジーである。
(2) (P∧Q) → (R∨P)=(¬P)∨(¬Q)∨(R∨P)=(¬P)∨P∨(¬Q)∨R
このとき、真理集合は全体集合Uなので、トートロジーである。
(3) (¬(P∧Q))∨P=((¬P)∨(¬Q))∨P=(¬P)∨P∨(¬Q)
このとき、真理集合は全体集合Uなので、トートロジーである。
(4) (P∧(¬Q)) → ((¬P) → Q)=((¬P)∨Q)∨(P∨Q)=(¬P)∨P∨Q
このとき、真理集合は全体集合Uなので、トートロジーである。 (終)
(追記) 令和5年9月19日付け
問題 x、y は有理数とする。
x+y と xy がともに整数ならば、x、y は整数であることを示せ。
(解) x+y=m、xy=n とおくと、m、nは整数で、x、y は、2次方程式 t2−mt+n=0 の
解である。解 t は有理数なので、 t=q/p (p、qは互いに素な整数) と書ける。
方程式に代入して、 q2/p2−mq/p+n=0 すなわち、 q2−mpq+np2=0 より、
q2=p(mq−np) となるので、q2 すなわち、q は p で割り切れる。
しかるに、p、qは互いに素な整数なので、p=±1 となる。
よって、解 t は整数となり、すなわち、x、y は整数である。 (終)
(コメント) この問題を背理法で示すには、どうすればいいのだろう?
「x、y は整数である」の否定は、「x、y の少なくとも一つは整数でない」で、上記の(解)か
ら、これは矛盾としていいのかな?
問題 ある仕事を、A、B、C の3人で行っても1時間以上かかるという。この仕事を、1人
が単独で行うとき、2時間以上かかるものが少なくとも2人いることを示せ。
(解) 「2時間以上かかるものが少なくとも2人いる」の否定は、
「2時間以上かかるものが1人以下」
すなわち、「2時間未満で終わらせるものが少なくとも2人いる」
すなわち、単独で、1時間あたり仕事全体の半分以上が終わるものが少なくとも2人いる
すなわち、この2人で、1時間より短い時間で仕事が終わることになる。
これは、「A、B、C の3人で行っても1時間以上かかる」ことに矛盾する。
したがって、2時間以上かかるものが少なくとも2人いる。 (終)
(追記) 令和7年4月25日付け
次の東北大学 前期文系(1992)の問題は、命題に関する問題である。
問題 自然数 n≧1 について、2種類のすべて相異なる命題P(n)、Q(n)がある。いま、P(n)
が正しいならば、Q(n+1)が正しく、Q(n)が正しいならば、P(n+1)も正しいことが証明されたと
する。このとき、次の問に理由をつけて答えよ。
(1) P(1)が正しいとき、Q(10)は正しいといえるか。また、P(10)はどうか。
(2) (1)の仮定に加えて、さらに、Q(9)も正しいとき、P(n)はどのような自然数に対して正しい
といえるか。
(解)(1) P(1)が正しいとき、条件より、Q(2)、P(3)、Q(4)、P(5)、Q(6)、P(7)、Q(8)、P(9)、Q(10)
の順に正しいことが分かる。よって、Q(10)は正しいといえる。P(10)が正しいかどうかは不明。
(2) P(1)が正しいとき、P(3)、P(5)、P(7)、P(9)、・・・ も正しいことから、すべての奇数nに
ついて、P(n)は正しい。さらに、Q(9)も正しいとき、P(10)が正しいことから、P(12)、P(14)、P(16)、
P(18)、・・・ も正しい。すなわち、10以上のすべての偶数nについて、P(n)は正しい。
したがって、P(n)が正しいといえるnの値は、
1、3、5、7、9、10、11、12、13、14、・・・ (終)
以下、工事中!


 15<x<20 の周辺が微妙で、ズームして見ると、
15<x<20 の周辺が微妙で、ズームして見ると、