１１９	令和６年度前期	一橋大学	文系	・・・	確率（数学Ａ）	やや難

一橋大学　前期文系（２０２４）

第５問　ｎを３以上の奇数とする。円に内接する正ｎ角形の頂点から無作為に相異なる３点
　　を選んだとき、その３点を頂点とする三角形の内部に円の中心が含まれる確率ｐ_ｎを求
　　めよ。

（解）　題意より、ｎ＝２ｍ＋１　（ｍ≧２　の自然数）　とおける。１点を境に左右にｍ個ずつ
　　に分かれる配置となる。

　　

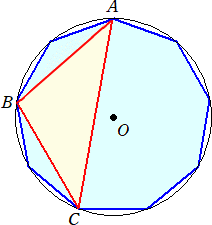
　選んだ３点を頂点とする三角形がＯを内部に含まないとき、最長の長さの線分ＡＣに関して
点Ｂは点Ｏの反対側にある。頂点Ａを定め、このような三角形ＡＢＣは、２点Ｂ、Ｃ を適宜決め
れば、ただ一つに定まる。

　Ａの決め方は、ｎ通りで、その１通りに対して、２点Ｂ、Ｃの決め方は、ｍ≧２として、

　_ｍＣ₂＝ｍ（ｍ−１）/２　（通り）　になるので、３点を頂点とする三角形がＯを内部に含まな

い場合の数は、　ｎ・_ｍＣ₂＝（２ｍ＋１）ｍ（ｍ−１）/２　（通り）

　起こり得る場合の数は、

　_ｎＣ₃＝（２ｍ＋１）（２ｍ）（２ｍ−１）/６＝（２ｍ＋１）ｍ（２ｍ−１）/３　なので、

よって、ｐ_ｎ＝１−３（ｍ−１）/（２（２ｍ−１））＝（ｍ＋１）/（２（２ｍ−１））＝（ｎ＋１）/（４（ｎ−２））

　ｍ＝１　のとき、明らかに、ｐ₃＝１ であるが、これは、上式で、ｍ＝１としたものである。

　したがって、　３以上の奇数ｎに対して、　ｐ_ｎ＝（ｎ＋１）/（４（ｎ−２））　　（終）


（コメント）　奇しくも、東京大学前期文系（２０２４）の第４問と類似問題であった。こんなこと
　　　　　が果たして起こるとは不思議だ！作問者が同じ人なのだろうか？



　　以下、工事中！