１１３	令和６年度前期	九州大学	理系	・・・	場合の数（数学Ａ）	やや易

九州大学　前期理系（２０２４）

第４問　ｎを３以上の整数とする。座標平面上の点のうち、ｘ 座標と ｙ 座標がともに１以上
　　ｎ以下の整数であるものを考える。これらｎ²個の点のうち３点以上を通る直線の個数を
　　Ｌ（ｎ）とする。以下の問いに答えよ。

（１）　Ｌ（３）を求めよ。
（２）　Ｌ（４）を求めよ。
（３）　Ｌ（５）を求めよ。

（解）（１）　下図より、Ｌ（３）＝３＋３＋２＝８

　　

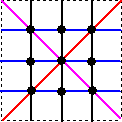
（２）　下図より、Ｌ（４）＝４＋４＋３×２＝１４

　　

（３）　下図より、Ｌ（５）＝５＋５＋５×２＋３×４＝３２

　　


　よおすけさんからのコメントです。（令和６年４月２７日付け）

　上記の問題の解答に目を通したとき、どこかで見たことある...と思ったら、

　お茶の間クイズ＆パズル：「点の連絡」

にありました。投稿は平成１６年８月２１日付けのアップなので、ほぼ２０年前？でしょうか。


（コメント）　よおすけさん、ありがとうございます。問題の趣旨が若干異なるので、類題とい
　　　　　うところでしょうか。



　　以下、工事中！