| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俀俇 | 暯惉俀侾擭搙慜婜 | 丂惷壀戝妛丂 | 丂棟宯 | 丒丒丒 | 峴楍偺値忔乮悢妛俠乯 | 丂昗弨 |
丂偙偺栤戣偼峴楍偺 値 忔偺揟宆栤戣偩傠偆丅悢妛嘥偵偍偗傞幃偺抣偺栤戣偺峴楍斉偱偁
傞丅
惷壀戝妛丂慜婜棟宯乮俀侽侽俋乯
| 丂峴楍 | 丂 |
丂偵偮偄偰丄師偺栤偄偵摎偊傛丅 |
乮侾乯丂俙亄俙2亄俙3丂傪媮傔傛丅
乮俀乯丂帺慠悢 値
偵懳偟偰丄丂俙亄俙2亄俙3亄丒丒丒亄俙3値-1亄俙3値丂傪媮傔傛丅
乮夝乯乮侾乯丂俠倎倷倢倕倷-俫倎倣倝倢倲倧値
偺掕棟傛傝丄丂俙2亄俀俙亄係俤亖俷
丂丂丂丂丂丂偙偺偲偒丄丂俙亄俙2亄俙3亖乮俙亅俤乯乮俙2亄俀俙亄係俤乯亅俙亄係俤
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖亅俙亄係俤
丂丂丂丂丂傛偭偰丄
丂丂丂丂丂丂丂丂丂![]()
乮俀乯丂俙亄俙2亄俙3亄丒丒丒亄俙3値-1亄俙3値
丂丂亖乮俙亄俙2亄俙3乯亄乮俙亄俙2亄俙3乯俙3亄丒丒丒亄乮俙亄俙2亄俙3乯俙3値-3
丂丂亖乮俙亄俙2亄俙3乯乮俤亄俙3亄丒丒丒亄俙3値-3乯
丂丂偙偙偱丄丂俙3亖俙乮亅俀俙亅係俤乯亖亅俀俙2亅係俙亖亅俀乮亅俀俙亅係俤乯亅係俙亖俉俤丂側偺偱丄
丂丂俙亄俙2亄俙3亄丒丒丒亄俙3値-1亄俙3値
丂亖乮侾亄俉亄俉2亄丒丒丒亄俉値-1乯乮亅俙亄係俤乯亖乮俉値亅侾乯乮亅俙亄係俤乯/俈
丂丂傛偭偰丄
丂丂丂丂丂丂丂![]() 丂丂乮廔乯
丂丂乮廔乯
乮僐儊儞僩乯丂夝摎帺懱偼堈偟偄両壨崌弇偺栤戣暘愅偱偼乽昗弨乿偲側偭偰偄傞偑丄偙傟偼偁偔
丂丂丂丂丂丂傑偱傕惷壀戝妛庴尡惗儗儀儖偵傛傞傕偺偱丄栤戣儗儀儖偲偟偰偼乽傗傗堈乿偩傠偆丅
丂峴楍偺惉暘傪尒偨弖娫偵丄
丂丂丂丂俙亖俀俼乮俀兾/俁乯丂乮尨揰拞怱丄俀兾/俁偺夞揮堏摦屻丄俀攞偺憡帡奼戝乯
偲婥偑偮偐傟偨撉幰偺曽傕懡偄偩傠偆丅峴楍
俙 偺屌桳懡崁幃偼丄丂倶2亄俀倶亄係亖侽丂偱偁
傞偑丄偦偺夝傪媮傔傞偲丄丂倶亖亅侾亇![]() 倝丂側偺偱丄侾偺俁忔崻 冎
傪梡偄傟偽丄曽掱幃偺
倝丂側偺偱丄侾偺俁忔崻 冎
傪梡偄傟偽丄曽掱幃偺
夝偑丄丂俀冎丂丄丂俀冎2丂偱偁傞偙偲傕尒偊偰偔傞丅
丂偙偺偙偲偵丄摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俽乮俫乯偝傫偑拝栚偝傟丄師偺傛偆側栤偄偐
偗傪側偝傟偰偄傞丅乮暯惉俀侾擭俁寧侾侾擔晅偗乯
丂俀師偺惓曽峴楍 俙 偑 俙2亄俙亄俤亖俷 傪枮偨偡偲偒丄俙
傪偡傋偰媮傔傛丅
乮夝乯丂幚悢惉暘偺丄俀師偺惓曽峴楍
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂![]()
丂丂丂偵懳偟偰丄俠倎倷倢倕倷-俫倎倣倝倢倲倧値
偺掕棟傛傝丄丂俙2亅乮倎亄倓乯俙亄乮倎倓亅倐們乯俤亖俷
丂丂丂俙2亄俙亄俤亖俷丂傛傝丄丂乮倎亄倓亄侾乯俙亖乮倎倓亅倐們亅侾乯俤
丂丂丂倎亄倓亄侾亗侽丂偺偲偒丄丂俙亖倠俤丂乮倠
偼幚悢乯丂偲偍偗傞丅
丂丂丂偙偺偲偒丄丂俙2亄俙亄俤亖俷丂偵戙擖偟偰丄丂乮倠2亄倠亄侾乯俤亖俷丂傛傝丄
丂丂丂丂丂倠2亄倠亄侾亖侽丂丂偙偺曽掱幃傪枮偨偡幚悢夝偼懚嵼偟側偄丅
丂丂丂傛偭偰丄丂倎亄倓亄侾亖侽丂偱丄偙偺偲偒丄丂倎倓亅倐們亅侾亖侽
丂丂丂丂偙偙偱丄丂倓亖亅倎亅侾丂傪戞俀幃偵戙擖偟偰惍棟偡傞偲丄
丂丂丂丂丂亅倎2亅倎亅倐們亅侾亖侽丂傛傝丄丂倐們亖亅倎2亅倎亅侾
丂丂丂倐亖侽丂偲偡傞偲丄曽掱幃丂倎2亄倎亄侾亖侽丂傪枮偨偡幚悢夝偼懚嵼偟側偄偺偱晄揔丅
丂丂丂傛偭偰丄丂倐亗侽丂偱丄丂們亖亅乮倎2亄倎亄侾乯/倐丂偲側傞丅
丂丂埲忋偐傜丄媮傔傞峴楍偼丄俀偮偺僷儔儊乕僞
倎 丄倐 偵傛傝丄
丂丂丂丂丂丂丂丂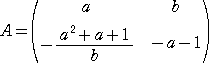
丂偙偺栤戣偼丄暯惉侾俆擭搙擖帋 嫗搒戝妛 棟宯偺栤戣乮仺嶲峫丗乽僆儊僈乮冎乯偺恀幚乿乯
傪堄幆偟偰丄峴楍偺栤戣偵偡傝懼偊傞偙偲偑偱偒傞丅
丂俀師偺惓曽峴楍 俙 偑 俙2亄俙亄俤亖俷
傪枮偨偡偲偒丄
丂乮俙100亄俤乯100亄乮俙2亄俤乯100亄俤亖俷
傪帵偣丅
乮夝乯丂俙3亖俤丂丄丂俙2亄俙亄俤亖俷丂側偺偱丄
丂丂丂乮俙100亄俤乯100亄乮俙2亄俤乯100亄俤亖乮俙亄俤乯100亄乮亅俙乯100亄俤
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖乮亅俙2乯100亄俙100亄俤
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖俙200亄俙100亄俤
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖俙2亄俙亄俤亖俷
乮僐儊儞僩乯丂俽乮俫乯偝傫偺弌戣偱偼丄
丂丂丂丂丂丂丂丂乮俙100亄俤乯100亄乮俙亄俤乯100亄俤亖俷
傪枮偨偣偽徹柧
丂丂丂丂丂偲側偭偰偄傞偑丄忋幃偼惉傝棫偨側偄偺偱丄懡暘乽儈僗僾儕乿丠