| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽侽俁 | 暯惉侾俁擭搙屻婜 | 嫗搒戝妛 | 棟宯 | 丒丒丒 | 懳悢寁嶼乮悢妛嘦乯 | 傗傗擄 |
丂怴妛廗巜摫梫椞乮暯惉侾俆擭傛傝幚巤乯偵傛傟偽丄悢妛嘦偵偍偗傞懳悢偺埖偄偼寉偔側偭
偰偄傞丅乮撪梕偺庢埖偄乯偵偼丄乽懳悢寁嶼偼埖傢側偄傕偺偲偡傞丅乿偲柧尵偝傟偰偄傞偔傜偄
偩丅
丂偟偐偟側偑傜丄嫵壢彂傪傒傞偲丄偦偙傑偱摜傒崬傫偩傕偺偼側偔丄娙扨側懳悢寁嶼乮掙偺曄
姺傪娷傓乯偐傜巒傑偭偰丄懳悢昞傪棙梡偟偨寘悢偺栤戣傗桳岠悢帤偑彫悢戞壗埵偐傜巒傑
傞偐側偳埲慜偐傜峴傢傟偰偄傞寁嶼偑偦偺傑傑偵巆偝傟偰偄傞丅偁傞嫵壢彂偵偼嵟崅埵偺
悢傪媮傔偝偣傞栤戣傕復枛栤戣偵偁傞丅
丂尰嵼偺偦偺傛偆側忬嫷壓偵偍偄偰丄師偺栤戣偼丄懳悢栤戣偺廔鄟傪忺傞偵憡墳偟偄栤戣
偲偄偊傞丅懡暘丄嶌栤傪偝傟偨曽偼懳悢栤戣偺壺傗偐側傝偟崰傪偛懚偠偺曽側偺偩傠偆丅
嫗搒戝妛丂屻婜棟宯乮俀侽侽侾乯
丂晧偱側偄幚悢 倎 偵懳偟丄侽亝倰亙侾 偱丄倎亅倰 偑惍悢偲側傞幚悢 倰 傪 乷
倎 乸 偱昞偡丅偡側傢
偪丄乷 倎 乸 偼丄倎 偺彫悢晹暘傪昞偡丅
乮侾乯丂乷 値倢倧倗10 俀 乸亙侽丏侽俀 偲側傞惓偺惍悢 値 傪侾偮媮傔傛丅
乮俀乯丂侾侽恑朄偵傛傞昞帵偱 俀値 偺嵟崅埵偺悢帤偑俈偲側傞惓偺惍悢 値 傪侾偮媮傔傛丅
丂丂丂偨偩偟丄丂侽丏俁侽侾侽亙倢倧倗10 俀亙侽丏俁侽侾侾丄侽丏俉係俆侽亙倢倧倗10 俈亙侽丏俉係俆侾丂偱偁傞丅
丂偙偺栤戣偼梊旛峑摍偺暘愅偱偼乽傗傗擄乿偲敾掕偝傟偰偄傞偑丄廫暘枮揰偑慱偊傞栤戣
偱傕偁傞丅忦審傪枮偨偡惓偺惍悢 値 傪慡偰媮傔傞偙偲偼擄偟偄偑丄侾偮偩偗夝傪尒偮偗傟
偽偄偄傢偗偱丄偦偺曽朄偼栤傢傟側偄偐傜偩丅
丂偨偩丄偙偺傛偆側弌戣宍幃偼怴孹岦偱丄姷傟偰偄側偄偲丄傗偼傝擄偟偄偐傕偟傟側偄丅
丂堦斒偵庴尡惗偑廗弉偟偰偄傞栤戣僷僞乕儞偼師偺傛偆側傕偺偱偁傠偆丅
丂俀18 偼丄壗寘偺悢偐丅傑偨丄嵟崅埵偺悢帤偼壗偐丅偨偩偟丄倢倧倗10俀亖侽丏俁侽侾侽
丂捠忢偼師偺傛偆偵夝偐傟傞丅乮傕偪傠傫丄庤寁嶼偱媮傔傞曽朄傕偁傞丅乯
丂丂倢倧倗10俀18亖侾俉亊倢倧倗10俀亖侾俉亊侽丏俁侽侾侽亖俆丏係侾俉
丂丂傛偭偰丄丂侾侽5亙俀18亙侾侽6 偐傜丄丂俀18 偼丄俇寘偺悢偱偁傞丅
丂偙偙偱丄丂倢倧倗10俀18亖俆丏係侾俉亖俆亄侽丏係侾俉丂偵偍偄偰丄丂丂倢倧倗10俀丏俇俀亖侽丏係侾俉俁
側偺偱丄丂倢倧倗10俀18佮倢倧倗10俀丏俇俀亊侾侽5丂傛傝丄丂俀18佮俀丏俇俀亊侾侽5亖俀俇俀侽侽侽
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮幚嵺偼丄俀18亖俀俇俀侾係係乯
丂偟偨偑偭偰丄丂嵟崅埵偺悢帤偼丄丂俀丂偱偁傞丅
丂嫗搒戝妛偺栤戣偼丄庴尡惗偑廗弉偟偰偄傞栤戣偺惓偵媡傪偄偭偰偄傞傢偗偱丄偦偺揰偱
傑偛偮偄偨曽偑懡悢偄傜傟偨偐偲巚偆丅
丂懳悢 倢倧倗 倃 偺抣偼丄巜昗乮惍悢晹暘乯偲壖悢乮彫悢晹暘乯偵暘偗傜傟傞丅巜昗偲壖悢偵偮
偄偰偼妛廗撪梕偐傜嶍彍偝傟偰偄傞偺偱丄栤戣暥拞偱愢柧偝傟偰偄傞丅悘暘愄偺崅峑惗
側傜丄乽巜昗偐傜寘悢偑暘偐傝丄壖悢偐傜悢帤偺攝楍偑暘偐傞乿偲嫵傢偭偨傕偺偩偑丄尰嵼
偼嫵偊傜傟偰偄側偄丅嫵偊傞懁偐傜偡傟偽丄壗偲側偔嵃偑敳偗偨傕偺傪嫵偊偰偄傞傛偆偱丄
僗僢僉儕偟偨惔椓姶偼摼傜傟側偄丅嫗搒戝妛屻婜棟宯偺栤戣偵弌夛偄丄愄偺崅峑帪戙偵
栠偭偨傛偆偵姶偠偨丅
丂傑偨丄嫗搒戝妛偺弌戣偼偲偰傕挌擩偱偁傞偲姶偠偨丅晛捠偩偭偨傜丄倢倧倗10俀亖侽丏俁侽侾侽
偲偟偰偟傑偆偲偙傠傪丄惓妋偵丄丂侽丏俁侽侾侽亙倢倧倗10 俀亙侽丏俁侽侾侾丂偲昞尰偟偰偄傞偐傜偱偁
傞丅
丂偁偔傑偱傕丄侽丏俁侽侾侽丂偼嬤帡抣偱偁傞偺偱丄倢倧倗10 俀丂偺抣傪晄摍幃偱昞偡曽偑惓偟偄
偲巚偆丅
丂偝偰丄慜抲偒偑挿偔側偭偰偟傑偭偨偑丄嫗搒戝妛偺栤戣傪夝偄偰傒傛偆丅
乮夝乯丂乮侾乯丂侽丏俁侽侾侽亙倢倧倗10 俀亙侽丏俁侽侾侾丂傛傝丄丂丂俁丏侽侾侽亙侾侽倢倧倗10 俀亙俁丏侽侾侾
丂丂丂丂傛偭偰丄丂丂侽丏侽侾侽亙乷侾侽倢倧倗10 俀乸亙侽丏侽侾侾丂偐傜丄丂乷侾侽倢倧倗10 俀乸亙侽丏侽俀
丂丂丂丂偟偨偑偭偰丄丂忦審傪枮偨偡惓偺惍悢 値 偲偟偰丄丂値亖侾侽
丂丂乮俀乯丂俀値 偺嵟崅埵偺悢帤偑俈偱偁傞偺偱丄丂倢倧倗10俈亝乷値倢倧倗10俀乸亙倢倧倗10俉
丂丂丂丂偙偙偱丄丂侽丏俉係俆侽亙倢倧倗10 俈亙侽丏俉係俆侾丄侽丏俋侽俁侽亙倢倧倗10 俉亙侽丏俋侽俁俁丂傛傝丄
丂丂丂丂侽丏俉係俆侾亝乷値倢倧倗10俀乸亙侽丏俋侽俁侽丂側傞傛偆側惓偺惍悢 値 傪尒偮偗傟偽傛偄丅
丂丂丂丂侽丏俁侽侾侽亙倢倧倗10 俀丂偵偍偄偰丄椉曈傪係俇攞偡傞偲丄丂侾俁丏俉係俇侽亙係俇倢倧倗10 俀
丂丂丂丂偝傜偵丄丂倢倧倗10 俀亙侽丏俁侽侾侾丂偵偍偄偰丄丂係俇倢倧倗10 俀亙侾俁丏俉俆侽俇
丂丂丂丂埲忋偐傜丄丂侽丏俉係俆侾亙侽丏俉係俇侽亙乷係俇倢倧倗10俀乸亙侽丏俉俆侽俇亙侽丏俋侽俁侽丂側偺偱丄
丂丂丂丂忦審傪枮偨偡惓偺惍悢 値 偲偟偰丄丂値亖係俇丂丂丂乮廔乯
乮僐儊儞僩乯丂値亖係俇丂偺敪尒偼丄乽侽丏俁侽侾侽乿偲偄偆悢偺摿庩惈偵埶懚偡傞偙偲偑懡偄丅
丂俵倝們倰倧倱倧倖倲幮偺 俤倶們倕倢 偵乽倢倧倗10 俀乿偺抣傪暦偔偲丄乽侽丏俁侽侾侽俀俋俋俋俆俇俇俁俋俉侾丒丒丒乿
偱偁傞丅偙傟傪棙梡偟偰丄乮俀乯偺忦審傪枮偨偡惓偺惍悢 値 偑丄侾侽侽侽侽傑偱偺偆偪偵壗屄偁
傞偐寁嶼偟偰傒偨丅
丂値亖係俇丄俆俇丄俇俇丄俈俇丄俉俇丄俋俇丄侾係俋丄侾俆俋丄侾俇俋丄侾俈俋丄丒丒丒丂偺寁俆俈俋屄懚嵼偡傞丅
丂偙傟傜偵偼摿暿側婯懃惈偼側偄傛偆偵姶偠傞偑丄忦審傪枮偨偡惓偺惍悢 値 傪婯掕偡傞
堦斒揑側岞幃偼懚嵼偡傞偺偱偁傠偆偐丅偙傟偼崱屻偺尋媶壽戣偲偡傞偙偲偵偟傛偆丅
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽俥俶乿偝傫偑丄忋婰偺栤戣偵偮偄偰峫嶡偝傟偨丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮暯惉俀俁擭侾侾寧俀俇擔晅偗乯
丂栤戣偺乮俀乯偺夝摎偱丄乽係俇乿偲偄偆悢偑撍慠弌偰偒傑偡丅榑棟揑偵偼壗傕栤戣偼偁傝傑偣
傫偑丄乽係俇乿偲偄偆悢偑弌偰偒偨崻嫆丄彮側偔偲傕婥暘偑傢偐傜側偄偲傢偐偭偨婥偵側傜側偄
偟丄椶戣傪夝偔嶲峫偵傕側傝傑偣傫丅
丂乮侾乯偱傕丄乽侾侽乿偲偄偆悢偑撍慠弌偰偒傑偡偑丄偙傟偼帺慠偱偡丅乮侾乯偺忦審偼丄
丂丂丂丂丂丂値丒倢倧倗10 俀亖倢倧倗10 俀値
偺彫悢晹暘偑侽丏侽俀傛傝彫偝偄悢傪侾偮媮傔傛偲偄偆偙偲偱偡偑丄偦傟偼丄俀値 偑 侾侽倣 傛傝
偪傚偭偲偩偗戝偒偄悢偑梸偟偄偲偄偆偙偲偱丄俀10乮=1024乯偑侾侽3乮=1000乯偲傎傏摍偟偔丄彮偟
偩偗戝偒偄偙偲偼摉慠堄幆偟偰偍偔傋偒偙偲偱偡丅
丂偝偰丄乮俀乯偱偡偑丄傕偟丄倢倧倗10 俈傗倢倧倗10俀偵偮偄偰偺忦審偑彂偄偰側偐偭偨傜丄偡傞偙偲
偼壗傕側偄偐傜丄嬶懱揑偵丄俀値傪丂俀丄係丄俉丄侾俇丄俁俀丄俇係丄侾俀俉丄俀俆俇丄俆侾俀丄丒丒丒偲彂偄
偰偄偔偼偢偱偡丅側偐側偐乽俈乿偱巒傑傞傕偺偼側偄側偲丅傕偪傠傫丄偙偺傛偆偵挷傋偰丄乽俈乿
偱巒傑傞傕偺偑尒偮偐傞傛偆偩偲栤戣偲偟偰惉棫偟傑偣傫丅
丂傕偆彮偟彂偄偰傒傞偲丄侾侽俀係丄俀侽係俉丄係侽俋俇丄俉侾俋俀丄侾俇俁俉係丄俁俀俈俇俉丄俇俆俆俁俇
巹偼丄庴尡惗偨傞傕偺偙偙傑偱偼偡傜偡傜彂偗傞傋偒偩偲巚偭偰偄傑偡丅偙偙傑偱偱丄愭摢偺
悢帤偲偟偰丄乽俈乿偲乽俋乿埲奜偼偡傋偰弌偰偄傑偡丅
丂廳梫側偺偼丄俀10乮=1024乯偱偡丅懄偪丄俀10傪偐偗傞偲慜偺曽偼偁傑傝偐傢傜側偄丅椺偊偽
俀3乮=8乯偵丄俀10傪偐偗傞偲丄俀13乮=8192乯偺傛偆偵丅俀1偐傜俀16傑偱偱愭摢偑乽俈乿偼側偄偱偡
偑乽俇乿偼偁傝傑偡丅俀6乮=64乯丄俀16乮=65563乯偱偡丅偙傟偵丄俀10乮=1024乯傪偐偗偰偄偗偽丄慜
偺曽偼丄抜乆偲丄俇俈丄俇俉丄俇俋丄俈侽偺傛偆偵側偭偰偄偔偲巚傢傟傑偡丅
丂偩偐傜丄俀16乮=65563乯偵俀10乮=1024乯傪偐偗偰丄偝傜偵俀10乮=1024乯傪偐偗偰ゥゥ偲傗偭偰偄
偗偽傛偄丅倢倧倗10 俈偲偐偑彂偄偰側偔偰傕偱偒傑偡丅偟偐偟丄倢倧倗10 俈偲偐偑彂偄偰偁傞偺偩偐
傜偦傟傪巊偆傋偒偱偟傚偆丅
乮乮俀乯偺夝乯
丂侽丏俁侽侾侽亙倢倧倗10 俀亙侽丏俁侽侾侾丂傛傝丄丂侾丏俉侽俇侽亙俇倢倧倗10 俀亙侾丏俉侽俇俇丂ゥ@(A)
(偙傟偼丄俀6乮=64乯傪儀乕僗偵俀10乮=1024乯傪偐偗偰偄偙偆偲偄偆偙偲偐傜弌偨幃偱丄俇傪偐偗傞偺偼帺慠偱偁傞)
丂摨條偵丄俁丏侽侾侽亙侾侽倢倧倗10 俀亙俁丏侽侾侾丂ゥ@(B)
(A)+(B)亊値丂傛傝丄
丂丂侾丏俉侽俇侽亄俁丏侽侾侽亊値亙乮俇亄侾侽値乯倢倧倗10 俀亙侾丏俉侽俇俇亄俁丏侽侾侾亊値
廬偭偰丄値偑彫偝偄偲偒丄(椺偊偽丄値亙侾侽)
丂丂侽丏俉侽俇侽亄侽丏侽侾侽亊値亙乷乮俇亄侾侽値乯倢倧倗10 俀乸亙侽丏俉侽俇俇亄侽丏侽侾侾亊値
丂偙偙偱丄値亖係偲偡傞偲丄丂侽丏俉係俇侽亙乷係俇倢倧倗10 俀乸亙侽丏俉俆侽俇
丂倢倧倗10 俈亙侽丏俉係俆侾亙侽丏俉俆侽俇丂偱丄侽丏俉俆侽俇亙侽丏俋侽俁侽亙倢倧倗10 俉丂偱偁傞偐傜丄
丂丂丂倢倧倗10 俈亙乷倢倧倗10 俀46乸亙倢倧倗10 俉
傛傝丄俀46 偺愭摢偺悢帤偼乽俈乿偱偁傞偙偲偑傢偐傞丅
丂丂丂丂忦審傪枮偨偡惓偺惍悢 値 偲偟偰丄丂値亖係俇丂丂乮廔乯
丂偝偰丄俀値 偺愭摢偺悢帤傪丄値亖侾偐傜値亖俁侽傑偱彂偄偰傒傞偲師偺傛偆偵側傝傑偡丅
俀丄係丄俉丄侾丄俁丄俇丄侾丄俀丄俆丄侾丄俀丄係丄俉丄侾丄俁丄俇丄侾丄俀丄俆丄侾丄俀丄係丄俉丄侾丄俁丄俇丄侾丄俀丄俆丄侾丄丒丒丒
丂婯懃惈偼側偄偱偡偑丄庛偄婯懃惈偵嬤偄傕偺偼偁傝偦偆偱偡丅乽侾乿偑尰傟傞昿搙偑嵟傕懡
偔丄師偑乽俀乿偺傛偆偱偡丅乽俈乿偼忋偺栤戣偵偁傞傛偆偵丄係俇斣栚偵巒傔偰尰傟丄乽俋乿偼俆俁斣
栚偵巒傔偰尰傟傑偡丅
丂偱偼丄椺偊偽丄乽侾乿偑尰傟傞妋棪偼丄偳偺掱搙偱偟傚偆偐丅偒偪傫偲彂偗偽
丂乷俀値乸傪10恑朄偱昞偟偨偲偒偺嵟崅埵偺悢偑乽侾乿偱偁傞傕偺偺屄悢傪N(値)偲偡傞丅
値 偑尷傝側偔戝偒偔側傞偲偒丄N(値)/値 偺嬌尷偼壗偩傠偆偐丠
乮僐儊儞僩乯丂俤倶們倕倢 偝傫偵乽侾乿偺弌尰昿搙傪寁嶼偟偰傕傜偭偨丅
丂丂俥俶偝傫偺寢壥偱偼丄丂俋/俁侽亖侽丏俁
丂丂値亖侾侽俀俁丂傑偱偺屄悢傪寁嶼偟偰丄丂俁侽俈/侾侽俀俁亖侽丏俁侽侽侾埵
丂丂壓恾偺昞偐傜椶悇偡傞偲丄俥俶偝傫偺栤戣偺摎偊偼丄乽侽丏俁乿偐側丠
丂丂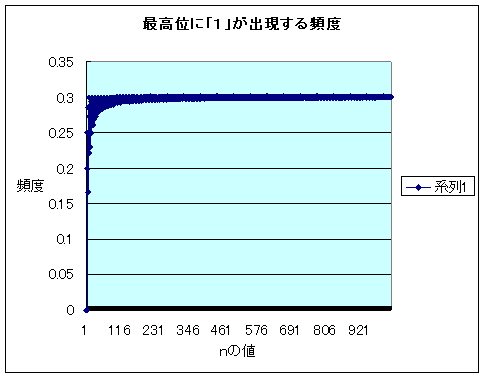
丂摉俫俹偺乽搳峞堦棗乿偺拞偺乽悢帤偺弌傗偡偝乿偲偄偆儁乕僕偑傑偝偵俥俶偝傫偺栤戣偵懳偡
傞夝摎偱偁傞偙偲傪丄峌棯朄偝傫偵偛嫵帵偄偨偩偒傑偟偨丅乮暯惉俀俁擭侾侾寧俀俈擔晅偗乯
丂偦傟偵傛傟偽丄媮傔傞妋棪偼丄丂倢倧倗10 俀亅倢倧倗10 侾亖侽丏俁侽侾侽丂偲側傝傑偡丅
丂堦斒偵丄嵟崅埵偺悢偑倣乮1亝m亝9乯偱偁傞妋棪偼丄
丂丂丂丂l倢倧倗10乮倣亄侾乯亅倢倧倗10 倣丂乮偨偩偟丄倢倧倗10 倶 偼忢梡懳悢乯
偱梌偊傜傟丄儀儞僼僅乕僪乮Benford乯偺朄懃偲偄偆偦偆偱偡丅乮仺丂嶲峫丗乽俙侽侽俉俋俆俀乿乯
丂俥俶偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俁擭侾侾寧俀俈擔晅偗乯
丂妋偐偵丄乽悢帤偺弌傗偡偝乿偵彂偄偰偁傞偙偲偲偐側傝偺娭楢偑偁傝丄摎偊偼丄倢倧倗10 俀 偱
偁傞偲巚偄傑偡丅偨偩丄偙偺栤戣偑弮慠偲悢妛偺栤戣偱偁傞偺偵懳偟丄儀儞僼僅乕僪偺朄懃
偼丄堦掕偺忦審偺傕偲偱嬤帡揑偵惉傝棫偮朄懃偩偐傜丄堦墳嬫暿偟偨曽偑偄偄偲巚偄傑偡丅
丂彮偟堦斒壔偟偰丄師偺宍偵偟偨曽偑徹柧偟傗偡偄偱偟傚偆丅
丂倎 偼柍棟悢丄0亝倐亝1丄値 偼帺慠悢偲偟丄値 埲壓偺帺慠悢 倠 偱丄0亝{倠倎}亙倐
傪枮偨
偡傕偺偺屄悢傪N(値)偲偡傞丅偙偺偲偒丄N(値)/値 偺 n 仺 亣 偺偲偒偺嬌尷偼丄倐
偱偁傞丅
丂徹柧偱偒偦偆偩偲巚偭偰偄傑偡偑丄徹柧偱偒偨傢偗偱偼偁傝傑偣傫丅偙傟偑徹柧偱偒偨偲偟
偰丄傕偲偺栤戣偺夝偑 倢倧倗10 俀 偱偁傞偙偲傪妋擣偟偰偍偒傑偡丅
丂傑偢丄倢倧倗10 俀 偼柍棟悢偱偁傞(徹柧偼丠)丅 倎=倐=倢倧倗10 俀 偲偍偔丅
丂俀倠 偺嵟崅埵偺悢偑侾丂佁丂0亝{倠倢倧倗10 俀}亙倢倧倗10 俀丂佁丂0亝{倠倎}亙倐
丂乽悢帤偺弌傗偡偝乿偵彂偄偰偁傞偙偲偱丄懡彮婥偵側傞偙偲偑偁傝傑偡丅乽偨偲偊偽丄奺帺帯
懱偺恖岥偲偐柺愊側偳丏丏丏丅乿偲偄偆婰弎偑偁傝傑偡偑丄偙傟偩偲搒摴晎導偺柺愊偲偐巗挰
懞偺恖岥偲偐傕擖傝偦偆偵姶偠傑偡丅
丂椺偊偽丄搒摴晎導偺柺愊偵偮偄偰挷傋偰傒傞偲師偺傛偆偵側傝傑偡丅
愭摢偺悢帤 丂1 2 3 4 5 6 7 8 9
搙丂 悢 丂丂丂丂8 4 3 10 4 6 6 3 3
丂儀儞僼僅乕僪偺朄懃偵廬偭偰傞姶偠偼偟傑偣傫丅悢偑彮側偄偙偲傕偁傝傑偡偑丄偦傟傛傝丄
乽庢傝摼傞抣偑廫暘峀斖埻偵峀偑偭偰偄偰乿偵奩摉偟偰偄側偄偙偲偑嵟戝偺棟桼偱偟傚偆丅
嵟彫偺崄愳偲嵟戝偺杒奀摴偱傕丄1丗100偵傕側傝傑偣傫丅偦傟偲搒摴晎導偲偄偆偺偼柧帯
惌晎偑摑帯偺搒崌偱嶌偭偨傕偺偱偡偐傜丄懨摉側戝偒偝偵偮偄偰偺僀儊乕僕偑偁偭偨偱偟
傚偆丅4偑10屄傕偁傞尨場偲巚偄傑偡丅
丂崙偺柺愊偲側傞偲丄嵟彫偲嵟戝偺斾偼(僶僠僇儞偼彍偄偰)1丗106 偖傜偄偼偁傞偐傜丄偁傞
掱搙惉傝棫偮偺偱偟傚偆丅擔杮偺巗挰懞偺恖岥偩偲偳偆側傞偐傢偐傝傑偣傫丅擔杮偺巗偺
恖岥側傜懯栚偱偟傚偆丅3丄4丄5 偺偁偨傝偑懡偔側傝偦偆偱偡丅
丂倎倲 偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俁擭侾侾寧俀俈擔晅偗乯
丂FN偝傫偺庡挘偼惓偟偄偱偡偹丅堦條暘晍掕棟傛傝惉傝棫偪傑偡丅
丂俥俶偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俁擭侾侾寧俀俉擔晅偗乯
丂崅偄儗儀儖偺悢妛偐傜尒傟偽丄偦傟傎偳擄偟偔偼側偄偺偩偲巚偄傑偡丅弶摍悢妛(崅峑悢
妛掱搙)偱徹柧偑偱偒側偄偐偲巚偄傑偡丅師偺傛偆側偙偲傪側傫偲側偔峫偊偰偄傑偡丅
丂倎 傪屌掕偟偰峫偊傞丅N(値)/値 偺 n 仺 亣 偺偲偒偺嬌尷偺懚嵼偼尵偊傞偲偟偰丄偙傟傪
倐偺
娭悢偲峫偊丄P(倐)偲偡傞丅P(倐)偺楢懕惈偼尵偊偦偆丅P(倐)偺忔朄惈 P(倐)P(們)=P(倐們)偑尵偊
傟偽丄P(倐)=倐 偼尵偊傞偩傠偆丅P(倐)偺忔朄惈偵偮偄偰偼丄楢懕惈偑偁傟偽丄倐丄們
偑桳棟悢
偲偟偰傕傛偄丅忔朄惈偺戙傢傝偵壛朄惈偱傕傛偄丅懚嵼丄楢懕惈丄忔朄惈偲俁偮傕偁傝傑偡丅
柍棟偐側丠
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俁擭侾侾寧俀俉擔晅偗乯
丂徹柧傪偪傖傫偲峫偊偰偄傞傢偗偱偼側偄傫偱偡偑丄e2兾i丒ka 傪峫偊偨傜徹柧偱偒傑偣傫偐
偹丠倠 偺憹壛偵懳偟偰丄扨埵墌忋傪摨偠妏搙乮嫍棧乯偢偮恑傓偺偱丄値 偑廫暘戝偒偗傟偽丄
偳偺堦晹暘傪偲偭偰傕乮偦偙偐傜兤=2兾ia恑傫偩晹暘偵傕摨偠夞悢巭傑偭偰偄傞偺偱乯摨偠枾
搙偵側傝傑偡傛偹丅偲丄摢偱偼峫偊偰偄傞傫偱偡偑丄偆傑偔傑偲傑傝傑偣傫丅
丂俥俶偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俁擭侾侾寧俀俉擔晅偗乯
丂妋偐偵姶妎揑偵偼傎傏柧傜偐偐側偲巚偊偨傝偟傑偡偑丄偦偺姶妎揑側婥暘傪徹柧偵帩偪
崬傓偙偲偑偱偒傑偣傫丅慜偵乽P(倐)偺懚嵼偲楢懕惈偲忔朄惈乿偲彂偒傑偟偨偑敿暘埲忋忕択
偱偡偑丄懡彮杮婥偱傕偁傝傑偡丅乽懚嵼偲扨挷惈偲b偑桳棟悢偺偲偒惉傝棫偮偙偲乿偺曽偑偄
偄偐側側偳偲巚偭偰偄傑偡丅偄偢傟傕摢偺拞偱傏乕偭偲峫偊偰傞偩偗偱丄巻偲墧昅傪帩偪偩
偡偲偙傠傑偱峴偭偰傑偣傫丅
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俁擭侾侾寧俀俈擔晅偗乯
丂尦偺栤戣偺夝摎偱偡丅
乮夝乯丂俀1乣俀n 偺偆偪嵟崅埵偺悢偑1偱偁傞傕偺偺屄悢偼丄乽俀n 偺寘悢亅侾乿偵摍偟偄丅
丂丂幚嵺偵丄俀倠 偺寘悢偑俀倠-1 偺寘悢傛傝戝偒偄 佁 俀倠 偺嵟崅埵偑1丂偱偁傞丅
丂丂偙偺偲偒丄俀n 偺寘悢偼丄倢倧倗10 俀n 偺惍悢晹暘亄侾丂側偺偱丄乽俀n 偺寘悢亅侾乿偼丄
丂倢倧倗10 俀n 偺惍悢晹暘偦偺傕偺偵側傞丅偡側傢偪丄N(値)=[倢倧倗10 俀n]=[値丒倢倧倗10 俀]丂側偺偱丄
丂値 仺 亣偺偲偒丄丂乮値丒倢倧倗10 俀亅侾)/n亙N(n)/n亝値丒倢倧倗10 俀/n丂傛傝丄
丂丂N(n)/n 仺 倢倧倗10 俀丂丂乮廔乯
乮僐儊儞僩乯丂俀1亖俀丄俀2亖係丄俀3亖俉丄俀4亖侾俇丄俀5亖俁俀丄俀6亖俇係丄俀7亖侾俀俉丄丒丒丒丂傪挱傔
丂丂丂丂丂丂偰偄傞偲丄寘偑侾偩偗忋偑偭偨弖娫偵嵟崅埵偑侾偵側傞偙偲偑桴偗傞丅
丂丂丂丂丂丂丂偩偐傜丄俀1乣俀n 偺偆偪嵟崅埵偺悢偑1偱偁傞傕偺偺屄悢偼丄乽俀n 偺寘悢亅侾乿
丂丂丂丂丂丂偵摍偟偄傢偗偩丅乽亅侾乿偼丄侾埵偺暘偲棟夝偡傟偽傛偄丅
丂丂丂丂丂丂丂傜偡偐傞偝傫偺夝摎偵姶摦偟傑偟偨丅
丂俥俶偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俁擭侾侾寧俀俈擔晅偗乯
丂側傞傎偳丅偒傟偄側夝摎偱偡偹丅堦斒壔偟偨宍偱徹柧偡傞傕偺偐側偲巚偄傑偟偨偑丄偦偆
偱傕側偄傛偆偱偡丅嵟崅埵偺悢偑丄乽2乿偲偐乽3乿偲偐偵側傟偽堦斒壔偟偨宍偵側傞偱偟傚偆偐丅
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俁擭侾侾寧俀俉擔晅偗乯
丂俀倠 偺嵟崅埵偑1偺偲偒丄俀倠+1 偺嵟崅埵偼丄乽2乿傑偨偼乽3乿偱偡偐傜丄嵟崅埵偑乽2乿傑偨偼
乽3乿偲側傞妋棪傕丄倢倧倗10 俀 偱偡丅
丂傑偨丄俀倠 偺嵟崅埵偑1偺偲偒丄俀倠-1 偺嵟崅埵偼丄乽5乿乣乽9乿偱偡偐傜丄嵟崅埵偑乽5乿乣乽9乿
偲側傞妋棪傕丄倢倧倗10 俀 偱偁傝丄偙傟偐傜丄嵟崅埵偑乽4乿偲側傞妋棪偼丄
丂丂侾亅俁倢倧倗10 俀亖倢倧倗10 俆亅倢倧倗10 係
偲媮傑傝傑偡丅懠偵丄嵟崅埵偑乽4乿乣乽7乿偲側傞妋棪傕媮傑傝傑偡偺偱丄寢嬊摨偠曽朄偱媮傑傞
偺偼丄
丂嵟崅埵偑乽1乿丂丂丂丂丂(妋棪亖倢倧倗10 俀)
丂嵟崅埵偑乽2乿乣乽3乿丂(妋棪亖倢倧倗10 俀)
丂嵟崅埵偑乽4乿丂丂丂丂丂(妋棪亖侾亅俁倢倧倗10 俀)
丂嵟崅埵偑乽5乿乣乽7乿丂(妋棪亖係倢倧倗10 俀亅侾)
丂嵟崅埵偑乽8乿乣乽9乿丂(妋棪亖侾亅俁倢倧倗10 俀)
傑偱偱偡偹丅寢嬊丄倢倧倗10 俀 偱昞偣傞傕偺偟偐媮傑傝傑偣傫偺偱丄乽1乿丄乽4乿埲奜偼堦斒壔偟
側偄偲擄偟偄偲巚偄傑偡丅
丂俥俶偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俁擭侾侾寧俀俉擔晅偗乯
丂嵟崅埵偑乽4乿偱偁傞妋棪偑摨偠曽朄偱媮傔傜傟傞偺偑柺敀偄偱偡偹丅俀倠傪俁倠偵曄偊偨傜丄
摨偠曽朄偱丄嵟崅埵偑乽1乿乣乽2乿偲嵟崅埵偑乽3乿乣乽8乿丄嵟崅埵偑乽9乿偑媮傔傜傟偦偆偱偡偹丅
丂偲偙傠偱丄俀倠偱傕俁倠偱傕寢壥偼摨偠偵側傞偼偢偱偡偑丄偙偺偙偲傪壗偐偆傑偄曽朄偱帵偣傞
偱偟傚偆偐丅