
4次以下の方程式には解の公式が存在するが、5次以上の方程式には存在しないので、
個々の場合については、解を近似的に求めることが主眼となる。
当HPでは、高次方程式の解の近似計算として、Hornerの方法をとりあげた。この方法
は、どんな方程式の近似解を求めることにも使えるが、解のおおよその値が分かっていて、
それを精密に求めていくというもので、そのおおよその値が分かっていないと使用が難しい
という弱点があった。
この方法を改良したものが、グレーフェの方法(Graeffe’s method)である。(1837年)
まず具体的な方程式に対して、グレーフェの方法の考え方を眺めてみよう。
例 2次方程式 X2−3X+2=0 は、(X−2)(X−1)=0 より、解 2 ,1 を持つ。
いま、この解が不明なものとし、以下のように考えて、解 2 ,1 の近似解を求める。
F(X)=X2−3X+2 とおく。このとき、
F(X)F(−X)=(X−2)(X−1)(−X−2)(−X−1)
=(X−2)(X+2)(X−1)(X+1)
=(X2−4)(X2−1)
=X4−5X2+4
ここで、 X2=Y とおき、 F1(Y)=F(X)F(−X) とすると、
F1(Y)=Y2−5Y+4
となる。
(このとき、 F1(Y)=0 は、解 4 ,1 を持つ。これは、ちょうど、F(X)=0 の解
2 ,1 を用いて、22 ,12 になっている点に注目すべきだろう。)
この操作を続ける。すなわち、 F2(Z)=F1(Y)F1(−Y) (Y2=Z)とおくと、
F2(Z)=Z2−17Z+16
である。 (このとき、 F2(Z)=0 は、解 24 ,14 を持つ。)
同様にして、F3(W)=F2(Z)F2(−Z) (Z2=W)とおくと、
F3(W)=W2−257W+256
である。 (このとき、 F3(W)=0 は、解 28 ,18 を持つ。)
解 28 ,18 の大きさを考えると、28 は、18 に比べて非常に大きいといえる。
そのため、F3(W)=0 の解と係数の関係において、
28 + 18 = 257 、 28 × 18 = 256
であるが、これは、ほぼ、 28 ≒ 257 、 18 ≒ 256/257 と考えてよいことを意
味する。
(解の近似値が方程式の隣り合う係数の比の(−1)倍で得られる点に注目すべきだろう。)
よって、元の解は、それぞれ 257 、256/257 の8乗根として近似解が得られる。
1837年当時は、対数全盛の時代であったから、この8乗根の計算は、対数表を用いて
簡単に近似計算が出来たに違いない。
(今の世でも普通の電卓には必ずといっていいほど、√キーがついている。
従って、2乗根は、√キーを1回、4乗根は、√キーを2回、8乗根は、√キーを3回たた
けば、瞬時に求められる。これは、グレーフェの方法にとっては、とても便利な機能だ。)
以上で述べたことを一般的に言い換えてみよう。
方程式 F(X)=anXn+an−1Xn−1+・・・+a2X2+a1X+a0 = 0 の n 個の実数解を、
α1 、α2 、α3 、・・・、αn (但し、|α1|>|α2|>|α3|>・・・>|αn|)
とする。 このとき、 F1(Y)=F(X)F(−X)=0 の解は、 α12 、α22 、α32 、・・・、αn2 で
ある。ただし、Y=X2 である。同様にして、
F2(Z)=F1(Y)F1(−Y) の解は、 α14 、α24 、α34 、・・・、αn4 で、Z=X4 である。
この操作を、m 回続ける。
Fm(V)=Fm−1(W)Fm−1(−W)
=bnXn+bn−1Xn−1+・・・+b2X2+b1dX+b0 = 0 の解は、
α12^m 、α22^m 、α32^m 、・・・、αn2^m で、 V=X2^m である。
このとき、解と係数の関係により、
α12^m +α22^m +α32^m +・・・+αn2^m = −bn−1/bn
α12^m・α22^m +α22^m・α32^m +・・・+αn−12^mαn2^m = bn−2/bn
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
α12^m ×α22^m ×α32^m ×・・・×αn2^m = (−1)nb0/bn
ところで、|αk|>|αk+1|より、|αk/αk+1|= L>1 なので、
|αk2^m /αk+12^m|= L2^m の値は、十分大きい m の値に対して、かなり大
きいと言える。
すなわち、十分大きい m の値に対して、|αk2^m|は、|αk+12^m|と比べて、かなり
大きいと考えてよい。
したがって、解と係数の関係により、
α12^m ≒ −bn−1/bn
α12^m・α22^m ≒ bn−2/bn より、α22^m ≒ −bn−2/bn−1
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
α12^m ×α22^m ×α32^m ×・・・×αn2^m ≒ (−1)nb0/bn より、
αn2^m ≒ −b0/b1
となる。(それぞれが、方程式の隣り合う2項の比の(−1)倍で与えられる。)
そこで、解 α1 、α2 、α3 、・・・、αn の近似値を求めるには、それぞれ 2m乗根を
とればよい。ただし、上記の計算からも分かるように、解の符号は、「+」 か 「−」 か分
からないので、解における関数値(組立除法を活用)から判断するしかない。
今度は、3次方程式に対して、グレーフェの方法を適用してみよう。
例 3次方程式 X3−2X+1=0 において、F(X)=X3−2X+1 とおく。
F(X)F(−X)=(X3−2X+1)(−X3+2X+1)=−X6+4X4−4X2+1
ここで、 X2=Y とおき、 F1(Y)=F(X)F(−X) とすると、
F1(Y)=−Y3+4Y2−4Y+1
となる。
同様にして、 F2(Z)=F1(Y)F1(−Y)=−Z3+8Z2−8Z+1 (Y2=Z)
F3(W)=F2(Z)F2(−Z)=−W3+48W2−48W+1 (Z2=W)
F4(V)=F3(W)F3(−W)=−V3+2208V2−2208V+1 (W2=V)
ここで、 α116 ≒ 2208 、α216 ≒ 1 、α316 ≒ 1/2208 であることがいえる。
ところで、2208 の16乗根のうち正のものは、だいたい 1.618079821 で、
このとき、 F(1.618079821)=2.000268317
F(−1.618079821)=−0.000268317 ( ← 誤差が小さい!)
だから、α1<0 で、 α1 ≒ −1.618079821
F(1)=0 なので、 α2 = 1
1/2208 の16乗根のうち正のものは、だいたい 0.6180164829 で、
このとき、 F(0.6180164829)=0.0000149523 ( ← 誤差が小さい!)
F(−0.6180164829)=1.9999850477
だから、α3>0 で、 α3 ≒ 0.6180164829
小数第3位までを考えると、3次方程式 X3−2X+1=0 の解は、
−1.618 、 1 、 0.618
であると言える。
因みに、実際に解いてみると、 X3−2X+1=(X−1)(X2+X−1) なので、
解の公式から、 X=1、(−1±√5)/2 となる。
√5 ≒ 2.236 なので、解はおおよそ、 1 、 0.618 、 −1.618 となり、
グレーフェの方法で得られたものに一致する。
(グレーフェの方法はとても単純である。いとも簡単に解の近似値が求められることに大変
感動した。ただ、累乗根の計算に電卓もしくは対数表を使わなくてはいけないが.....。)
今度は、4次方程式に対して、グレーフェの方法を適用してみよう。
例 4次方程式 12X4+4X3−21X2+2X+3=0 の近似解を求めよ。
(上式をみて、解が、−3/2、−1/3、1/2、1 であることは、因数定理を知っていれば直ぐ分かる
ことだろう。ここでは、解を不明なものとして、グレーフェの方法の素晴らしさを堪能して下さい。)
機械的に計算するために、その構造を検証してみよう。
F(X)=a4X4+a3X3+a2X2+a1X+a0 に対して、
F1(Y)=F(X)F(−X)=b4Y4+b3Y3+b2Y2+b1Y+b0 とおくと、簡単な計算から、
b4=a42
b3=−a32+2a4a2
b2=a22−2a3a1+2a4a0
b1=−a12+2a2a0
b0=a02
であることが分かる。この式だけをみると、いかにも面倒な計算という雰囲気があるが、次
のように図示すると、その構造が明らかとなる。
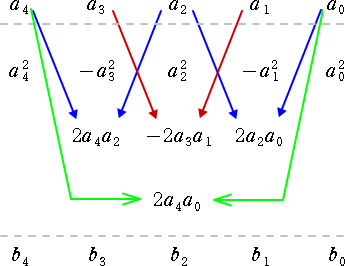
この構造を踏まえて、順次、次のように計算される。
