無理数を近似する分数 　　　　　　　　　　　　　　　　　

正の有理数 Ｘ に対して、正の有理数		を作る。	この有理数を新たに Ｘ として、同
様の操作を繰り返すと、だんだんと、 （≒１．７３２）に近づく。

　実際に、計算してみると、

上記の次の値が、１６８/９７≒１．７３２０ なので、ほぼ「１．７３２」までは正しい値と判断して
よいだろう。

　７回程度の分数計算で無理数の近似値が求まるが、これが「速いか遅いか」は判断の分
かれるところである。

　 ≒ １．７３２０５０８０７５６８８８ に到達するのに、上記の計算が何回位必要か、計算
してみた。（但し、初期値として、Ｘ＝１ と設定）

　　　　　［実行結果］　　　　　　　　　表計算ソフト Ｅｘｃｅｌ のＶＢＡスクリプト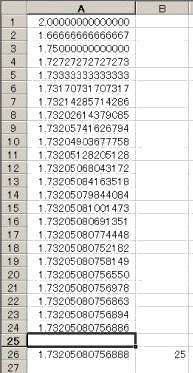

　　　Sub 平方根3の近似()
　　　Dim N, X As Variant
　　　N = 1
　　　X = 1
　　　Range("A1").Select
　　　Do Until Abs(X - 1.73205080756888) < 1E-14
　　　X = (X + 3) / (X + 1)
　　　If Abs(X - 1.73205080756888) < 1E-14 Then
　　　　With ActiveCell
　　　　　　　　　　　　　.Offset(1, 0).Value = X
　　　　　　　　　　　　　.Offset(1, 1).Value = N
　　　　End With
　　　Else
　　　　With ActiveCell
　　　　　　　　　　　　　.Value = X
　　　　　　　　　　　　　.Offset(1, 0).Select
　　　　End With
　　　N = N + 1
　　　End If
　　　Loop
　　　　　　　　　　　　 　　　　　　　　 End Sub

　上記の実行結果から、 の近似値として小数点以下第１４位まで一致させるために、２５
回の計算が必要であることが分かる。（１．７３２程度でよければ、７回位）


　このページでは、無理数がある分数により近似できること、さらによい近似となる分数が簡
単にできること、そしてその性質等についてまとめておきたい。

　 を近似する分数としては、

　　　　　　　　　

が有名である。（参考：平方根２を求める数列）

　この分数は、ニュートン・ラフソン法により、微分を用いて求められる。

これに対して、

という分数は、微分を用いないで求められる点が優れている。

　Ｘ ＝ から、Ｘ²＝３ なので、両辺に Ｘ を加えれば、Ｘ²＋Ｘ ＝ Ｘ＋３

すなわち、Ｘ(Ｘ＋１) ＝ Ｘ＋３ より、

Ｘ ＝

となる。もっとも、Ｘ²＝３ から、２Ｘ²＝ Ｘ²＋３ と変形して、両辺を ２Ｘ で割れば、

Ｘ＝

が得られるので、わざわざ微分を用いなくてもよかったのかもしれない。

が、に収束する様子は、次のグラフから分かる。

　　　　　　　　

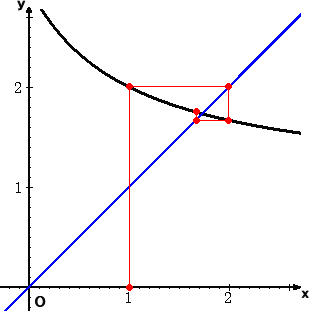
　 の値の左右交互に近似値が現れ、しかも、だんだんと の値に近づいている。

このことを、性質としてまとめれば、次のようになる。

（１）　 に近い正の有理数を Ｘ とし、

の値を Ｙ とおく。

　　　このとき、 は、Ｘ と Ｙ の間にあり、Ｙ は、Ｘ よりもよい の近似値である。

（２）　Ｘ と の間にある次の有理数

　　　　　　　　

　　　は、Ｘ、Ｙ よりもよい の近似値である。

　証明は易しいので、読者の練習に残しておこう。

（参考文献：石谷　茂　著　不等式の解法と証明　（大阪教育図書））


　当ＨＰがいつもお世話になっているＳ（Ｈ）さんから、この話題に関する問題を頂いた。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２１年５月１４日付け）

とおく。次の問いに答えよ。

（１）　Ｆ（）＝　であることを示せ。

（２）　ｘ≧０　ならば、　Ｆ（ｘ）≧２　であることを示せ。

（３）　ｘ≧２　、ｙ≧２　ならば、　｜Ｆ（ｘ）−Ｆ（ｙ）｜≦｜ｘ−ｙ｜/１００　であることを示せ。

（４）　ｘ≧２　ならば、　｜Ｆ（Ｆ（ｘ））−｜≦｜ｘ−｜/１００００　となることを示し、

　　　これを用いて、｜ｒ−｜＜１０^-4　を満たす有理数 ｒ を １つ求めよ。

（コメント）　わずか２回の計算で、１０^-4　のオーダーとは、収束が速いですね！
　　　　　　Ｓ（Ｈ）さんに感謝します。



　　　　以下、工事中