分数の意味　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　分数は、小学校算数の一つの壁といわれる。多くの児童がつまづくところらしい。それまで、
１とか２とか絶対的な値だと思わせていた数に対して、分数との出会いで、どうも違う感覚を
児童に要求するところに原因があるようだ。

　比の学習が小学校算数のメインテーマの一つだと思うが、分数の、比としての感覚を身に
つけないまま進級してしまうので、その後の学習で支障をきたすことになる。高校生でも分数
を見ると、「計算の手が止まってしまう」という生徒も数多い。比の計算（分数の計算）は、数
学に限らず、化学など、自然科学全般で必要とされる計算技法の一つである。比の感覚は、
是非身につけてほしいと願うところである。

　分数は、３つの顔を持つ数である。

（１）　方程式の解としての表現（割り算の表現）

　　　整数係数の１次方程式がいつも解けるように、新しい数を創造。

　例　　方程式　３Ｘ＝６　の解は、Ｘ＝６÷３＝２　である。

　　　　（実は、この計算は、数学が苦手な人にとって、かなり難しい計算のようだ。
　　　　　Ｘ を求めるために、両辺を ３ で割るという発想は、浮かばないらしい。
　　　　　３を何倍したら、６になるかを考えて、Ｘ＝２ という解を発見する人が多い。）

　上記のように割り切れる場合は、どんな人にとっても、それほどの困難さは感じられない。

　　ところが、方程式　３Ｘ＝２　の解を問われると、数学が苦手な生徒は考え込んでしまう。
　多分、それは自然な反応だと思う。今まで知っていた数の中に、３に掛け算して２となる数
　が存在しないからである。

　　数学では、この場合、新しい数― 分数 ―を創造して、Ｘ＝２/３　とする。

　　即ち、方程式　ａＸ＝ｂ　の解は、ａ≠０ である限り、機械的に、Ｘ＝ｂ÷ａ　と考えて解き、
　ｂ÷ａ という計算を分数 ｂ/ａ で表現しようということである。（→　参考：「割り算の意味」）

　　　（注意）　広島工業大学の大川研究室からコメントをいただいた。一部修正して、紹介し
　　　　　　　たいと思う。

　　　　　　　例えば、分数 １２/３ には、

　　　　　　　　　３ を Ｘ 回加えて１２になるように定めた解であるという見方（包含除）
　　　　　　と、
　　　　　　　　　Ｘ を ３ 回加えて１２になるように定めた解であるという見方（等分除）

　　　　　　の２通りがある。すなわち、

　　　　　　ａＸ＝ｂ （ａ≠０）の解として、Ｘ＝ｂ/ａ があるわけだが、その解の意味として、

　　　　　　　　　　　ａＸ を、ａ・Ｘ とする見方と、Ｘ・ａ とする見方

　　　　　　の２通りの見方があるということである。

　　　　　　　大川研究室でも指摘していることであるが、交換法則 ＡＢ＝ＢＡ が成立するので
　　　　　　結果的に同じ値になり、同じ記号で表されるということになる。 ＡＢ＝ＢＡ があまり
　　　　　　にも当たり前と認識されるため、両者の差異のことを、皆すぐ忘れるのだろうとの
　　　　　　ことである。
　　　　　　（私も大川さんと同様に昔、小学校で習ったような気がするが、あまり両者を特段
　　　　　　 に区別して意識したことはないように思う。全く不都合が起こらなかったので意識
　　　　　　 することがなかったと言う方が正しいかもしれない．．．ちょっと、反省！）

（２）　単位１に対する絶対的な値としての表現（全体に対する割合としての表現）
　　　　（中国的な考え方といわれる）

　　例　　分数 ２/３ は、単位１を３等分して、それを２つ分集めた量として把握される。

　　　　ここで混乱が起こる原因は、単位１という量そのものが、時と場所によって変化する点
　　　であろう。
　　　　例えば、３００人に対する２/３という量と、３００００人に対する２/３という量は明らかに
　　　異なるが、それぞれに対して、２/３という絶対的な値は同一である。

　　例　分数の計算　１/２＋１/３　で、１/２は単位１を２等分したものが１個分、１/３は単位
　　　　１ を３等分したものが１個分である。すなわち、

それぞれ個数数え上げの単位となる量（大きさ）が異 　　なり、このままの形では計算できない。

　　　　個数数え上げの単位をそろえるために、単位１を６等分したものを考える。このとき、
　　　１/２は、３個分で、１/３は、２個分となる。すなわち、あわせて５個分である。

　　　　　　

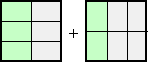
　　　　　したがって、１/２＋１/３＝５/６　という計算が成り立つ。

　　（コメント）　１/２＋１/３の計算で、よく誤答例と引き合いに出されるのが、
　　　　　　分子＝１＋１＝２　、　分母＝２＋３＝５　だから、１/２＋１/３＝２/５
　　という計算である。もちろん、数学（算数）の計算としては誤りであるが、

　　　　Ａの皿には、２個の果物がのっていて、うち１本はバナナである。
　　　　Ｂの皿には、３個の果物がのっていて、うち１本はバナナである。
　　今、２つのお皿Ａ、Ｂを一つのお皿に移すと、そこには、
　　　　５個の果物がのっていて、うち２本はバナナである。

　　これって、雰囲気は、「１/２＋１/３＝２/５」という感じ。だから、こういう計算をしがちな人
　をなぜか非難することができないネ！


（３）　基準の量に対する比較としての表現
　　　　（ギリシャ的な考え方といわれる）

　　例　分数　２/３　は、何か基準となる量ではかると、一方が２個分、他方が３個分という比
　　　　較を表す場合にも用いられる。
　　　　　比較は通常、「 ２ ： ３ 」という形で表現されるが、「：」の間に「−」を付け加えれば、
　　　　「÷」という記号になり、　２ ： ３ ＝２÷３＝２/３　ということが理解される。

　　例　勝ち目（ｏｄｄｓ）という言葉がある。これは、事象の確率を比で表す方法である。
　　　　例えば、さいころを投げて、６の目が出る確率は、１/６ 、６の目以外の目が出る確率
　　　　は、５/６ であるので、６の目に賭けるときのオッズは、１：５（＝０．２）となる。

　競馬等にもオッズという言葉があるが、これは上記とは違うようだ。

ある券に賭けられた金額に対する、全賭け金から諸経費を差し引いた払戻金の割合をオッ
ズと呼ぶ。（実際はもっと複雑で、こんな単純な計算ではオッズは求められない。）

例　ある競馬のレースで、Ａ君は、ある券を１００円を出して買った。
　　そのレースの全賭け金額は１００万円で、諸経費は２０万円であった。Ａ君の買った券の
　　賭け金総額が、５万円のとき、その券のオッズは、（１００−２０）÷５＝１６．０（倍）となる。
　　したがって、もしＡ君の買った券が勝てば、Ａ君は、１００×１６．０＝１６００（円）を手にす
　　ることができる。
　　　（私自身、これまで競馬の馬券等を購入した経験がないので、オッズに詳しい方、上記
　　　　の文章で何か間違いがあればご指摘ください。）


（追記）　平成３０年９月２０日付け

　分数の問題です。

　ある分数の分母に８を加えると１/３で１３を加えると１/４になるという。この分数を求めよ。

（解）　ある分数を　ｙ/ｘ　とおくと、　ｙ/（ｘ＋８）＝１/３　、　ｙ/（ｘ＋１３）＝１/４

　　　よって、逆数を考えて、　ｘ/ｙ＋８/ｙ＝３　、ｘ/ｙ＋１３/ｙ＝４

　　　辺々引いて、　５/ｙ＝１　より、　ｙ＝５

　　　このとき、　ｘ＋８＝１５　より、　ｘ＝７

　　　よって、求める分数は、　５/７　　（終）

　この問題を文字を使わずに解くことは可能でしょうか？


　ＰＢさんからのコメントです。（平成３０年９月２０日付け）

　出来上がる二つの分数は分子が同じで分母の差が５、それらが１/３、１/４　に等しくなる。

これらの分母は差が１なので、分子・分母を５倍して、　５/１５、５/２０

　よって、元の分数は、　５/７

．．．という解答ではいかがでしょうか？


　ｔｅｔｓｕさんからのコメントです。（平成３０年９月２０日付け）

　８と１３の差５が１/３、１/４の分子・分母に使われている数の1に相当します。言い換えれ

ば、文中の１/３、１/４は、約分する前のもとの分数に使われている数字で分母に8や13を

加えた段階では、それぞれ５/１５、５/２０であったと考えられます。

　ということは、もとの分数は分子が５、分母は、１５−８　または　２０−１３で７。

つまり、もとの分数は、５/７。


　ハンニバル・フォーチュンさんからのコメントです。（平成３０年９月２０日付け）

　逆数の世界で考えてから、また元の世界に戻るのはいかがでしょうか。逆数の世界での問
題は、以下のように考えました。

《ある分数の分子に８を加えると３で１３を加えると４になるという。この分数を求めよ。》

　これならば、【ある分数の分子に５を加えると１になる】ことは自明です。従いまして、分母
は５です。

　分母が５であるような、ある分数の分子に８を加えると３となるということです。

言い換えれば、

　分母が５であるような、ある分数の分子に８を加えると１５/５となるということです。従いま
して、ある分数は、７/５でした。

　以上は逆数の世界での出来事でしたから、元の世界に戻れば、求めるべき分数の値は、
５/７となります。


（コメント）　皆さんの素晴らしい閃きに感動しました。