パスカルの定理　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　「人間は考える葦」で有名なパスカル(1623〜1662)は、下記のような興味ある定理を証明
した。

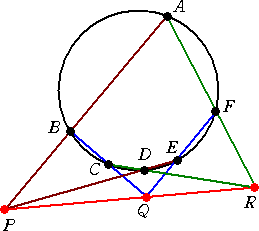円周上の６点Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆについて、 左図のように直線を引き、その交点をＰ、Ｑ、Ｒ とすると、３点Ｐ、Ｑ、Ｒは一直線上にある。 　　　証明は、方べきの定理やメネラウスの定理を 　　活用してなされる。 　（複素数による証明→「複素数の底力」を参照）

（証明）　　下図において、３点Ｐ、Ｑ、Ｒが一直線上にあることを示すには、

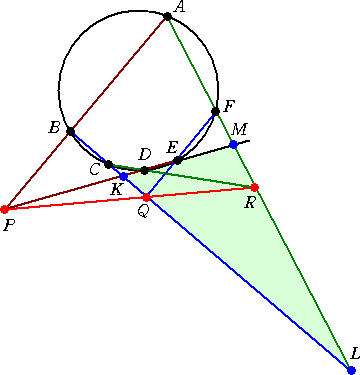△ＫＬＭについて、 　　 が成り立つことを示せばよい。 　まず、△ＫＬＭと３直線ＡＢ、ＣＤ、 ＥＦについて、 　ＫＢ/ＢＬ・ＬＡ/ＡＭ・ＭＰ/ＰＫ＝１ 　ＫＣ/ＣＬ・ＬＲ/ＲＭ・ＭＤ/ＤＫ＝１ 　ＫＱ/ＱＬ・ＬＦ/ＦＭ・ＭＥ/ＥＫ＝１ が成り立つ。 　　これらを辺々掛け合わて、次式 　を得る。

ＫＱ/ＱＬ・ＬＲ/ＲＭ・ＭＰ/ＰＫ・ＫＢ/ＢＬ・ＫＣ/ＣＬ・ＬＡ/ＡＭ・ＬＦ/ＦＭ・ＭＤ/ＤＫ・ＭＥ/ＥＫ＝１

　方べきの定理を意識して、

　　　ＫＢ/ＢＬ・ＫＣ/ＣＬ・ＬＡ/ＡＭ・ＬＦ/ＦＭ・ＭＤ/ＤＫ・ＭＥ/ＥＫ

　＝｛（ＫＢ・ＫＣ）/（ＤＫ・ＥＫ）｝・｛（ＬＡ・ＬＦ）/（ＢＬ・ＣＬ）｝・｛（ＭＤ・ＭＥ）/（ＡＭ・ＦＭ）｝

　＝１

なので、したがって、

　

が成り立つ。　（証終）

（コメント）　何とか図をコンパクトにまとめようと結構苦労しました．．．　ｆ(^^;) 。円周上の
　　　　　　任意の６点で、定理が成り立つことの凄みが実感できました！

　パスカルが偉いところは、上記の定理が、円に限らず、一般の円錐曲線（楕円・放物線・
双曲線）においても成り立つことを示したことだろう。しかも、１６歳で．．．。
　（絶句！私の１６歳は何をしていたっけ．．．？化学部で水質検査にはまっていたような．．．。）

　何となく、楕円や放物線のときの図はイメージしやすいので、双曲線の場合を図示してお
こう。

　　　

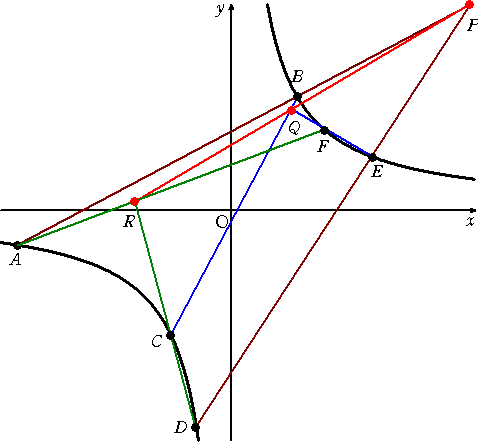
　円錐曲線は、円錐を平面で切った切り口として現れる。このことは、紙の上方に光源を置
いて紙に描いた円の投影として我々の眼前に実現できるということである。円の場合のパ
スカルの定理の図をＯＨＰシートなどに描いて、そのシートを適当に傾けると楕円や放物線
や双曲線の場合のパスカルの定理の図が見て取れる。

　このパスカルの定理は、２直線に対しても成り立ち、パッポスの定理と呼ばれている。

パッポスの定理

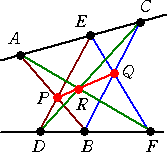２直線の一方に３点 Ａ、Ｃ、Ｅ があり、他方に３点 　Ｂ、Ｄ、Ｆ があるものとする。 　　このとき、左図のように直線を引き、その交点を 　Ｐ、Ｑ、Ｒ とすると、３点 Ｐ、Ｑ、Ｒ は一直線上にある。

（証明）　下図において、３点Ｐ、Ｑ、Ｒが一直線上にあることを示すには、△ＫＬＭについて、

が成り立つことを示せばよい。 まず、△ＫＬＭと３直線ＥＤ、ＢＣ、ＡＦについて、 　　 　　 　　 が成り立つ。 　これらを辺々かけて、

ＫＰ/ＰＬ・ＬＱ/ＱＭ・ＭＲ/ＲＫ
　　　　　　　　　　　　　×（ＫＢ/ＢＬ・ＬＦ/ＦＭ・ＭＤ/ＤＫ）・（ＫＡ/ＡＬ・ＬＥ/ＥＭ・ＭＣ/ＣＫ）＝１

　△ＫＬＭについて、３点 Ｂ、Ｆ、Ｄ および Ａ、Ｅ、Ｃ は一直線上にあるので、

　　　　ＫＢ/ＢＬ・ＬＦ/ＦＭ・ＭＤ/ＤＫ＝１　、　ＫＡ/ＡＬ・ＬＥ/ＥＭ・ＭＣ/ＣＫ＝１

したがって、

　　

が成り立つ。　（証終）



　　以下、工事中！