菱形の驚くべき性質 　　　　　　　　　　　　　　　　　　　　　　　　　

　当ＨＰがいつもお世話になっているＨＮ「DD++」さんからの投稿です。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２８年５月２９日付け）

　三角関数の計算と初等幾何学との対応を研究（→　参考：「四角形の面積」）していたとこ
ろ、驚きの発見をしたので紹介します。

　問題（中学3年生の応用問題レベル）

　菱形ABCDで、対角線ACとBDとの交点をOとします。辺BC上に∠DAEが鋭角になる範囲
で点Eを取り、3点 B、O、D から線分AEに対して垂線 BP、OQ、DR を下ろします。

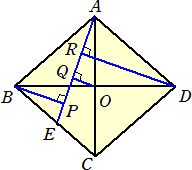このとき、 　　　　　２AQ＝AP＋AR　および　２OQ＝DR−BP 　　　が成り立つことを証明してください。

（解）　線分BRと線分OQの延長との交点をFとします。DR//OF　かつ　OはBDの中点なの
　　　で、中点連結定理の逆より、FはBRの中点で、２OF＝DRです。

　　　　　　　　

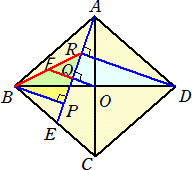
　　　BP//FQ　かつ　FはBRの中点なので、再び中点連結定理の逆より、QはPRの中点で、
　　２FQ＝BP　です。∠DAEが鋭角なので、点Aは線分PR間にはなく、

　　　２AQ＝(AQ−PQ)＋(AQ＋PQ)＝AP＋AR

　　となります。また、　２OQ＝２(OF-FQ)＝DR−BP　となります。　　（終）


　どうですか驚いたでしょうと、これだけで言ってもサッパリ伝わらないと思いますので、以下
解説。

　勘のいい方はお分かりと思いますが、菱形の性質でこの証明に使ったものは対角線の交
点が中点であることくらいで、点Aも線分PRの外にあることしか使っていません。

　つまり、これ自体は一般の平行四辺形と適当な直線と適当な外分点を使っても成り立ち
ます。しかし、わざわざ平行四辺形を菱形に限定し、外分点を菱形の頂点に限定したこと
で、この２式が面白い意味を持つようになるのです。

　AB＝BC＝CD＝DA＝１　として、角度に注目してみましょう。ここから高校数学になります。

(1)　∠OAB＝∠OAD＝α、∠OAE＝∠OBP＝∠ODR＝β とおいてみる。

　　直角三角形ABPを考えると、　BP＝sin(α−β)、AP＝cos(α−β)
　　直角三角形ADRを考えると、　DR＝sin(α＋β)、AR＝cos(α＋β)

　また、OA＝cosα なので、　OQ＝cosαsinβ　、AQ＝cosαcosβ

　つまり、この２式はそれぞれ積和の公式

　　２cosαcosβ＝cos(α−β)＋cos(α＋β)
　　２cosαsinβ＝sin(α＋β)−sin(α−β)

　を意味することになります。

(2)　∠ABO＝∠ADO＝α、∠OAE＝∠OBP＝∠ODR＝∠β とおいてみる。

　　直角三角形ABPを考えると、　BP＝cos(α＋β)、AP＝sin(α＋β)
　　直角三角形ADRを考えると、　DR＝cos(α−β)、AR＝sin(α−β)

　また、OA＝sinα なので、OQ＝sinαsinβ、AQ＝sinαcosβ

　つまり、この２式はそれぞれ積和の公式

　　２sinαcosβ＝sin(α＋β)＋sin(αーβ)
　　２sinαsinβ＝cos(α−β)−cos(α＋β)

　を意味することになります。

(3)　∠DAE=α、∠BAE=β とおいてみる。

　　直角三角形ABPを考えると、　BP＝sinβ、AP＝cosβ
　　直角三角形ADRを考えると、　DR＝sinα、AR＝cosα

　また、∠OAB＝(α＋β)/２　なので、OA＝cos((α＋β)/２)　で、

　∠OAE＝(α−β)/２　なので、

　OQ＝cos((α＋β)/２)sin((α−β)/２) 、AQ＝cos((α＋β)/２)cos((α−β)/２)

　つまり、この２式はそれぞれ和積の公式

　　cosα＋cosβ＝２cos((α＋β)/２)cos((α−β)/２)
　　sinα−sinβ＝２cos((α＋β)/２)sin((α−β)/２)

　を意味することになります。

(4)　∠ABP＝∠CDR＝α、∠ADR＝∠CBP＝β とおいてみる。

　　直角三角形ABPを考えると、　BP＝cosα、AP＝sinα
　　直角三角形ADRを考えると、　DR＝cosβ、AR＝sinβ

　また、∠OBA＝(α＋β)/２　なので、OA＝sin((α＋β)/２) で、

　∠OAE＝∠OBP＝(α−β)/２　なので、

　OQ＝sin((α＋β)/２)sin((α−β)/２) 、AQ＝sin((α＋β)/２)cos((α−β)/２)

　つまり、この２式はそれぞれ和積の公式

　　sinα＋sinβ＝２sin((α＋β)/２)cos((α−β)/２)
　　cosβ−cosα＝２sin((α＋β)/２)sin((α−β)/２)

　を意味することになります。

　つまり、高校数学で習う三角関数の和と積の変換公式８種は、正体を暴いてみれば、実
は、中学３年生でも理解できる程度の簡単な菱形の性質を大変ややこしく書いただけにす
ぎないのでした。いやー驚き。


（コメント）　いやー本当に驚きですね！DD++さんの洞察力溢れる展開に感動しました。